基于變形控制的密排管幕頂管施工順序優化分析

陳 凱

(中鐵二十四局集團安徽工程有限公司, 合肥 230011)

引言

在城市中修建下穿隧道,為保護周邊環境,可以采用在管幕支護下的暗挖或預制隧道頂進施工方法。 管幕施工法是在管棚法的基礎上發展起來的,利用微型頂管技術將鋼管或其他材料制成的管道頂推到擬建地下建筑周圍。 管幕可視為水平鋪設的鋼管樁,這些排列緊密的鋼管樁通過嵌槽封層或凍結等輔助施工方法,形成擋土、擋水的超前支護,使大斷面隧道得以在軟土地層中通過。 然而,管幕施工也會對附近地層產生一定的擾動,部分學者對管幕頂進引起的地表沉降進行研究。 談力昕等以拱北隧道管幕施工段為例,采用2 種不同的計算方式對頂進力進行了估算,并與實際頂進力進行對比驗證[1];熊昊翔等從經驗參數選取是否合理的角度,對頂力的計算進行研究[2];何超等基于土體的極限平衡條件對拱頂和拱腳進行穩定性驗算,得出頂管間距的控制式[3];劉楊等研究管幕施工參數以及對地表變形的影響[4-6];潘偉強依托上海14 號線桂橋路站管幕段實例工程,對軟土地區管幕群頂管施工地面沉降監測與分析[7]。 劉方等采用數值模擬對3 種預加固方案(水平旋噴樁、管幕和小導管注漿)進行結構變形和受力分析[8]。 閆振虎等以重慶鐵路樞紐東環線新白楊灣下穿高速公路隧道工程為依托,采用有限元分析軟件MIDAS-GTS NX,研究淺埋隧道大管幕支護力學特性及施工控制技術[9]。 韓現民等以迎澤大街下穿太原市火車站通道工程暗挖段管幕-結構法施工為例,采用數值計算對鋼管不同頂進次序對地表沉降影響進行分析[10]。 何君佐采用實時監測手段對管幕群頂進過程中各鋼管的姿態與變形進行記錄,研究各類鋼管在頂進過程中的相互作用以及管幕群貫通閉合后的姿態與變形規律[11]。 程盼盼等以上海軌道交通14 號線桂橋路車站渡線段為依托,對管幕頂進和開挖階段進行模擬分析,并優化相關施工參數[12]。 雷升祥等依托太原市迎澤大街下穿火車站通道工程,應用離散元仿真軟件對新管幕通道施工方法進行模擬,研究施工過程中火車軌道沉降及雨棚柱基礎的位移變化[13]。 江勇濤等結合文林山隧道工程,采用螺旋出土套管頂進工藝進行管幕施工,提出單管頂進施工地表沉降計算方法,并引入群管施工地表沉降修正函數建立管幕群管施工地表沉降計算方法[14]。張宇以北京平安里地鐵車站工程及其實測數據為基礎,對密排橫向管幕進行解析分析[15]。 李登等采用“無縫”連接的矩形曲線頂管,在土體中形成弧形底部托盤對內部空間進行保護[16]。 李洋等給出曲線管幕施工過程中頂推力的計算公式,得到曲線管幕施工地鐵車站對周圍地層的影響規律[17]。 于源龍結合福州工業北路延伸線工程,采用數值軟件Midas 對多根管幕頂進過程地層應力分布情況及地表最大沉降位移情況進行分析[18]。 宋大勇等以北京軌道交通新機場線一期工程1#區間風井兼盾構接收井為例,介紹了區間風井施工過程中采用管幕法工藝[19]。 牛野采用ABAQUS 有限元分析軟件對復合地層下的群管頂進順序及地層沉降展開研究[20];唐正等依托上海田林路下穿中環隧道工程,對地表位移實測數據進行了詳細分析[21];王子君針對沈陽地鐵市府大路站,研究采用小直徑管幕工法施工的地鐵暗挖車站引起的地層及主體結構的位移變形規律[22]。

上述研究主要針對某一工程研究管幕施工對地層的擾動,對管幕的施工順序對地層擾動的影響并未深入分析。 基于此,采用三維數值分析方法,考慮“上排和下排的先后、連續頂入和間隔頂入”頂入順序,研究不同管幕施工順序對地表沉降的影響規律;揭示頂管間距對土拱效應的影響機理,定量評價密排頂管群施工過程中的管間土拱效應減少頂管施工過程引起的地表沉降量。

1 工程概況

合肥濱湖科學城大連路為城市主干道,其中某段隧道工程在樁號5+87.45 ～6+81.15 處下穿合肥市駱崗機場跑道,平面交角69°,隧道與綜合管廊工作井圍護樁間水平最小凈距4.87 m,頂部覆土5.3 ～6.13 m。管幕頂進施工過程易引起機場跑道變形,甚至是局部塌陷。 為保護既有機場主跑道,采用在管幕保護下的預制隧道頂進法施工,頂進長度約93.7 m。 管幕采用44 根壁厚16 mm?1.6 m 長鋼管,頂進長度為92.7 m。采用2 臺?1.6 m 泥水平衡頂管機,由東工作井往西接收井進行掘進施工,鋼管單節長不小于6 m,分節間采用鴛鴦坡口焊連接。 管幕暗挖段與機場主跑道平面位置關系見圖1。

2 數值模型概況

2.1 有限元模型設計

管幕頂管區間主要穿越雜填土和膨脹黏土的復合地層。 管幕密集頂管分布和頂進順序均為對稱,為了提高計算效率,取1/2 對稱邊界建模,沿隧道軸線方向(y軸)長93 m,沿隧道橫向(x軸)寬50 m,沿地表向下(z軸)深32 m。 模型四周側邊界設置水平約束,底部邊界設置固定約束。 現場鉆孔樁揭露,地下水位埋深16 m,高壓旋噴樁加固區域為端頭區加固。 數值模型共劃分368 298 個單元,產生507 919 個節點,網格數值仿真模型見圖2。

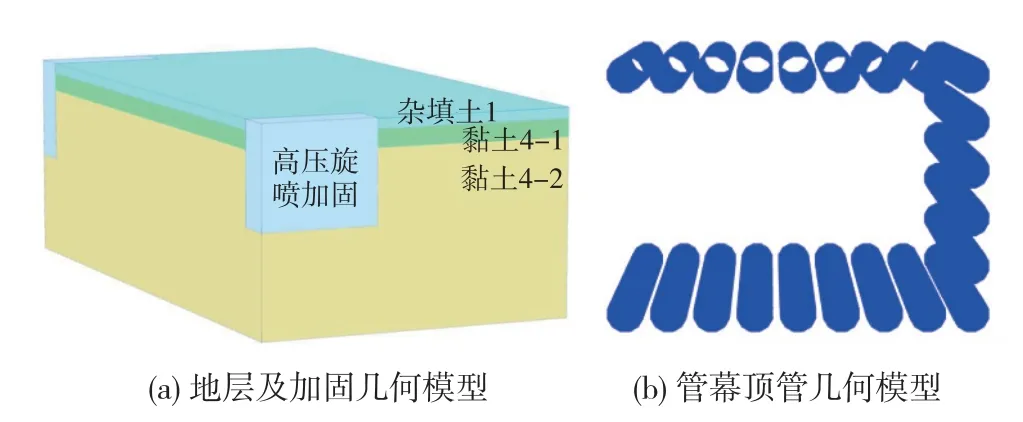
圖2 密排管幕幾何與網格模型

2.2 材料參數

軟件采用Plaxis3D。 圍巖采用10 節點高階四面體實體單元進行模擬,圍巖力學行為采用小應變土體硬化模型(HSS)進行描述。 管道鋼管采用板單元模擬,假定為線彈性材料。 模型中圍巖參數根據項目工程地質資料概化而來,結構單元參數根據結構設計資料及單元特性選取,模型基本輸入參數見表1、表2。

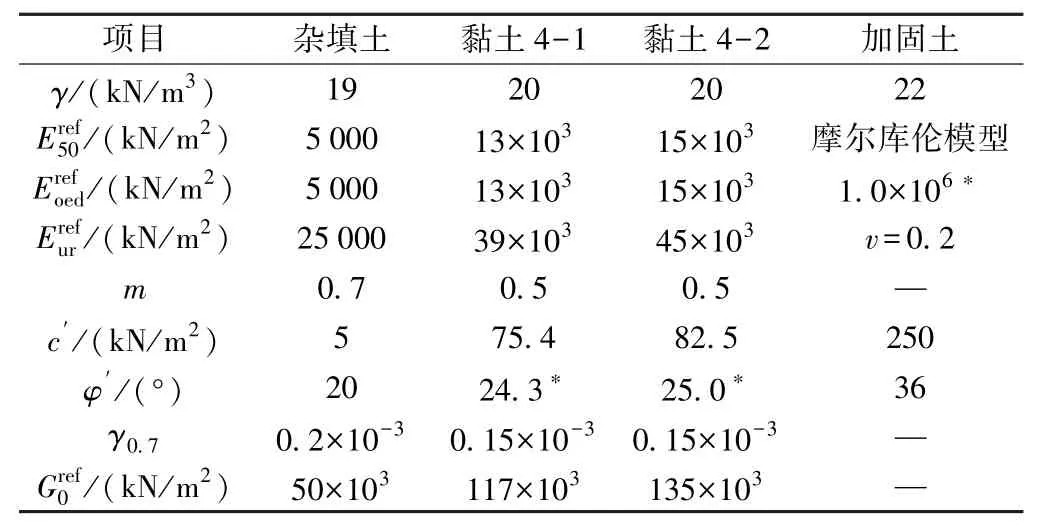
表1 圍巖材料計算參數

表2 板單元材料參數

3.3 計算工況

根據設計與實際施工情況,管幕頂進施工中,設計3 種方案進行對比研究。

方案1:始發井基坑開挖支護至下排管幕鋼管處,先施工下排管幕,再自下而上施工側排管幕,最后施工上排管幕。 該方案施工上排及側排管幕時需要搭設鋼管支撐架頂進作業平臺,下排及上排鋼管頂進均自中間向兩邊依次頂進,采用2 臺泥水平衡頂管機,見圖3(a)。

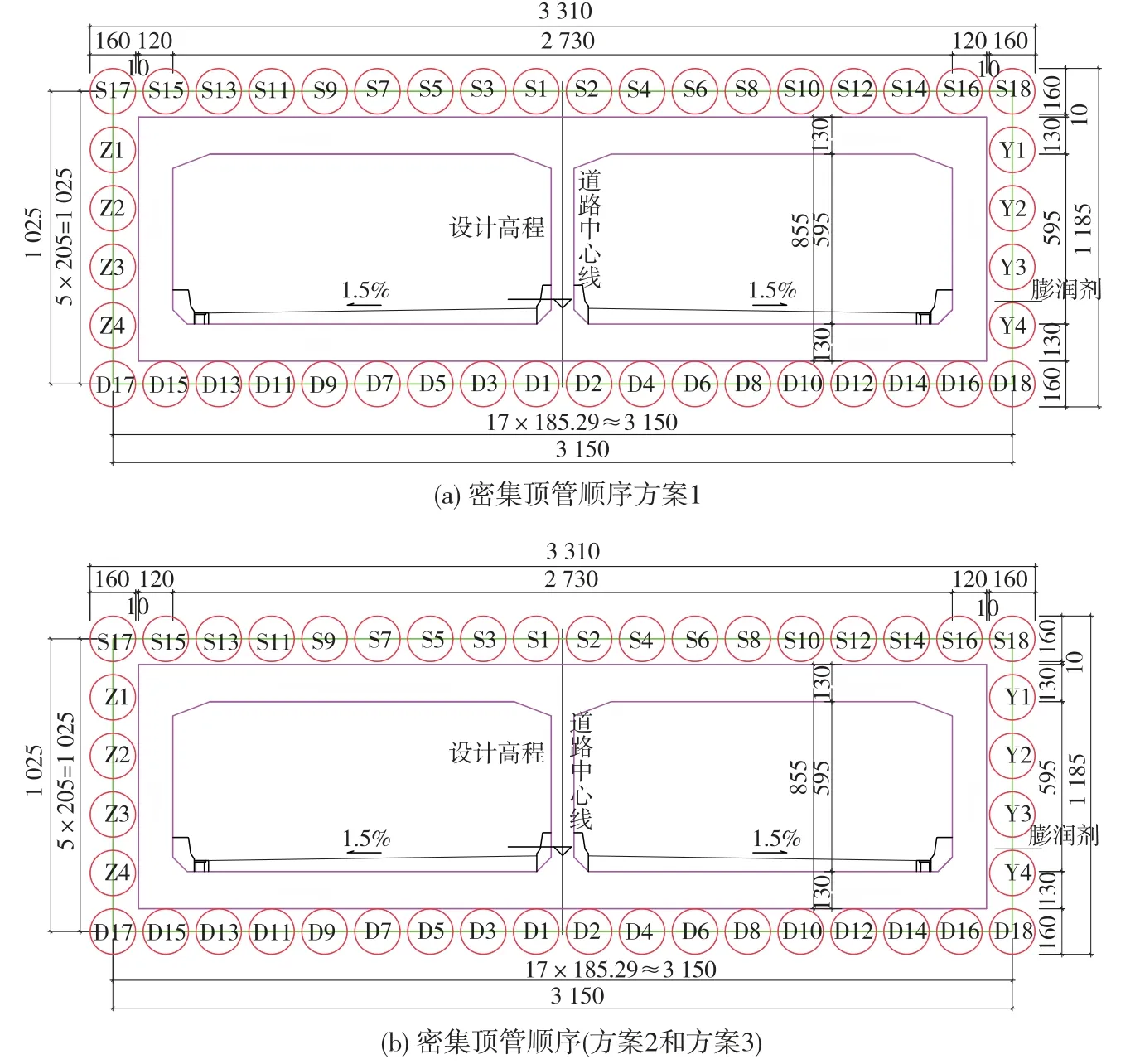
圖3 管幕密集頂管施工順序示意(單位:cm)

方案2:先施工上排管幕,其次自上而下依次施工側排管幕,最后施工下排管幕,該方案無需搭設鋼管支撐架頂進作業平臺,基坑開挖自上而下根據管幕施工分層分次開挖,下排及上排鋼管頂進均自中間向兩邊依次頂進,采用2 臺泥水平衡頂管機,見圖3(b)。

方案3:施工順序基本同方案2,不同之處在于下排及上排鋼管頂進均自中間向兩邊間隔1 根樁頂進,見圖3(b)。

3 管幕頂進順序對地表變形影響分析

3.1 不同方案橫向沉降對比

對于不同管幕頂管順序,地層變形的程度不同。共設置3 種頂管施工順序。 輸出同一個位置(y=47)的橫剖面地表沉降曲線,見圖4(x=0 m 為模型對稱邊界)。

由圖4 可知,3 種方案地表變形差異并不顯著。沉降極值與變形規律都比較接近。 方案3 的沉降極值最大,方案2 沉降極值最小,方案1 居中,分別為-13.34 mm、-12.27 mm 和-12.83 mm。 沉降影響范圍基本相同(34 m 左右)。

3.2 不同方案最大沉降曲線對比

管幕頂管過程中,管幕中間地表位置(x=0 m,y=47 m,z=0 m)始終為最大沉降位置,該位置沉降曲線見圖5。

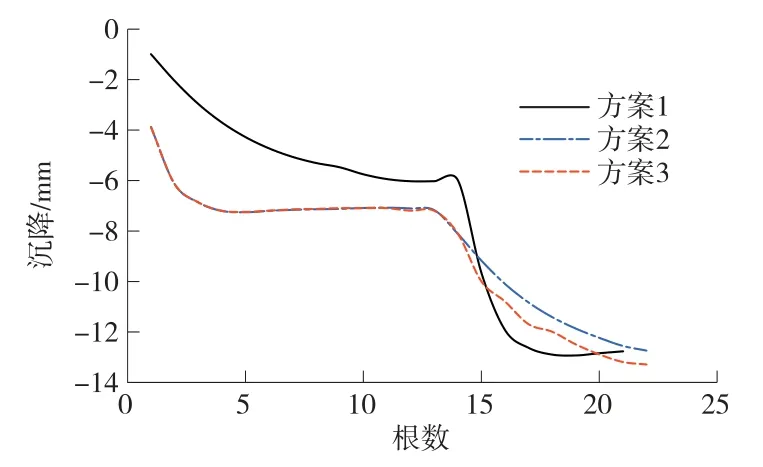
圖5 不同頂管施工順序下最大沉降

由圖5 可知,方案1 先施工下排頂管,第1、2 根頂管引起地表沉降增量較大,隨后引起的沉降增幅逐漸減少,主要原因是后續頂管距離中心沉降最大位置越來越遠;當上排頂管(第14 根)開始頂進,最大沉降值迅速增加。 方案2 和方案3 中,上排和側排施工順序相同,沉降曲線也基本相同,施工下排(第14 根)頂管時,方案3 引起的沉降較方案2 大,說明方案3 間隔頂進難以發揮相鄰頂管的遮擋限位作用。

4 土拱效應分析

4.1 單管沉降增量分析

管幕頂管頂進過程中,先施工的頂管可以形成一定的土拱效應。 為了對比分析下排頂管與上排頂管在不同順序工況下地層的響應特征。 分別輸出方案1 和方案2 數值模型的施工下排第4 根頂管引起的階段位移(見圖6、圖7)。

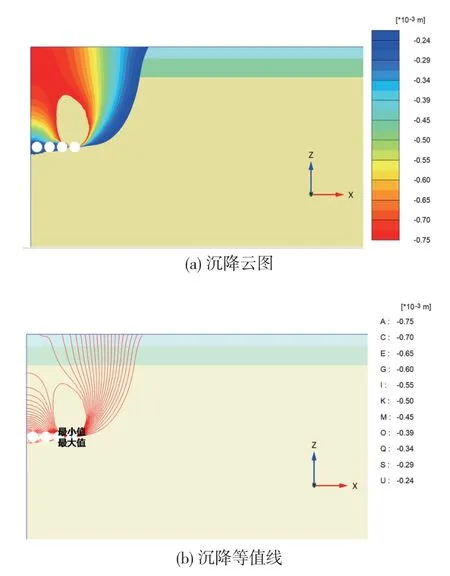
圖6 方案1 下排第4 根鋼管引起的變形

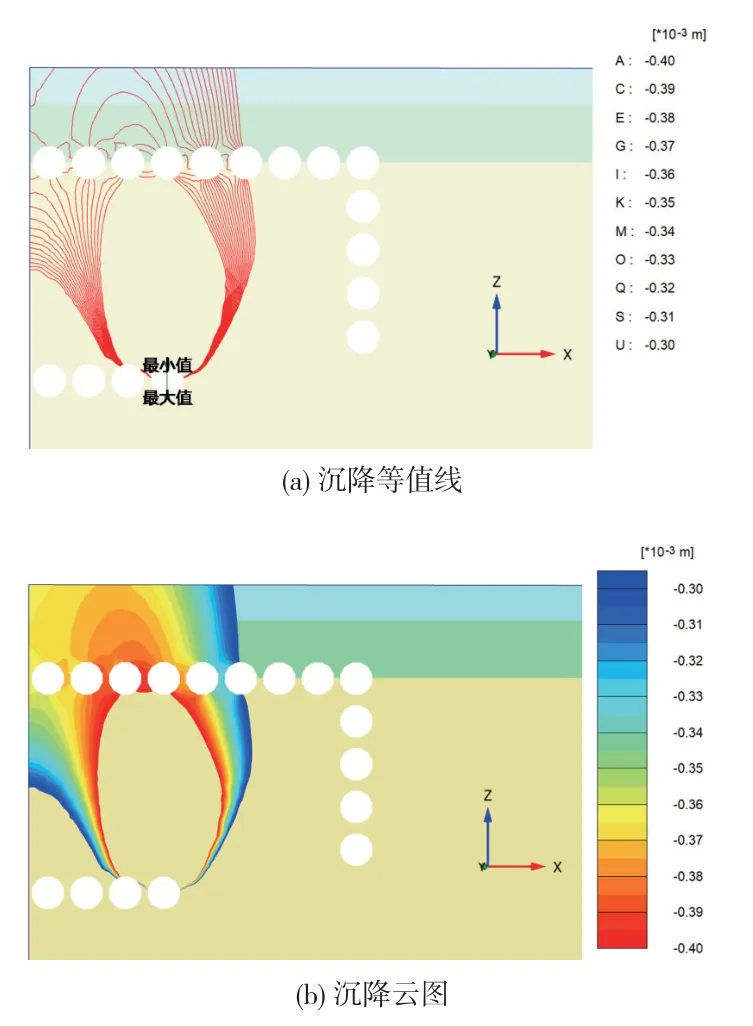
圖7 方案2 下排第4 根鋼管引起的變形

由圖6 可知,下排第4 根頂管頂入引起的沉降等值線直接平滑延伸到地表,等值線無明顯折皺和彎曲。沉降影響范圍邊界呈現上大下小的形態。 由圖7 可知,先施工完成上排頂管的方案2 中,施工下排第4 根頂管引起的沉降被上排頂管干擾發生彎曲。 在上排每兩根頂管之間位置,形成“拱形”的位移等值線,在所考慮的施工階段,上排頂管上方的沉降明顯小于其下方沉降,表明上排頂管形成土拱效應,可起到保護下排頂管的作用。

4.2 整體沉降分析

方案1 和方案2 管幕施工完成后的地層沉降云圖見圖8。

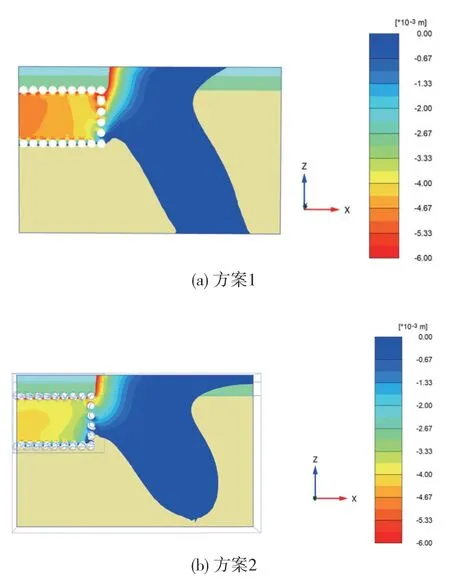
圖8 模型剖面最終地層沉降云圖

對比發現,管幕頂管完成后,在上排先施工的情況下,側排頂管頂入后周邊地層沉降更小,管幕圍成的隧道主體區域內的沉降也更小。 由此可見,先施工上排頂管可以更好控制下排頂管施工的擾動。 密排管幕頂管群最佳的順序為先施工管幕上排頂管,再施工管幕兩側及下排頂管。 因此,選擇方案2 作為工程的施工方案。

5 密排管幕施工過程地表變形特征分析

5.1 地表沉降影響范圍隨頂管變化規律

為了進一步分析管幕頂管進度對地表的變形影響,對方案2 分別取頂管完成根數為1 根、8 根、13 根、22 根時的地表沉降,對比不同進度的地表沉降情況,沉降云圖見圖9、圖10。 由于22 根頂管全部完成,整個地層獲得的最大沉降值為13 mm,為了對比不同施工階段地層擾動范圍,借鑒其他專題經驗(如地基沉降分層總和法計算深度Zn取附加應力等于自重應力的10%的標高作為壓縮層的下限),將10%的最大沉降值(1.3 mm)定義為影響區域的邊界臨界值。

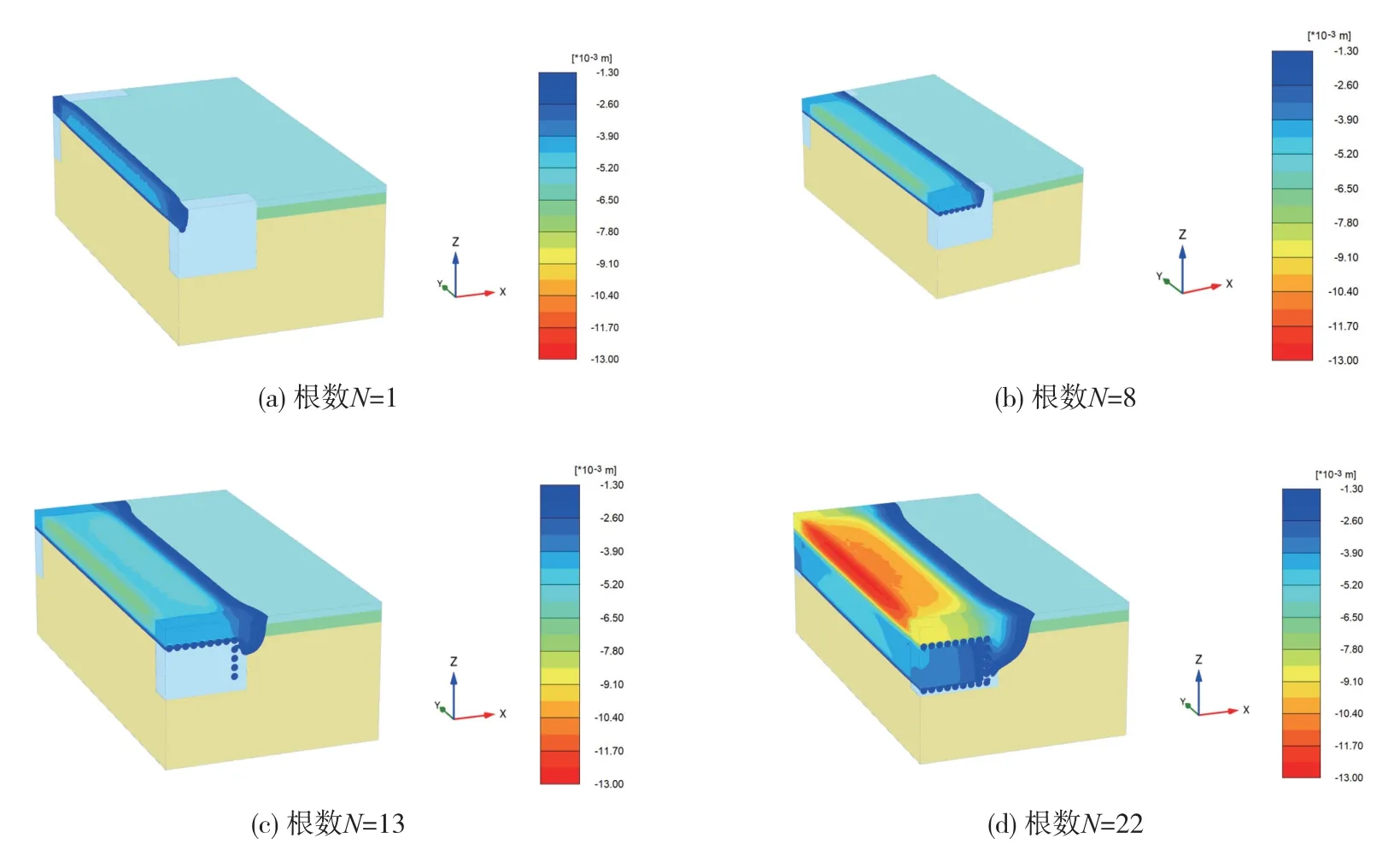
圖9 整體模型沉降云圖

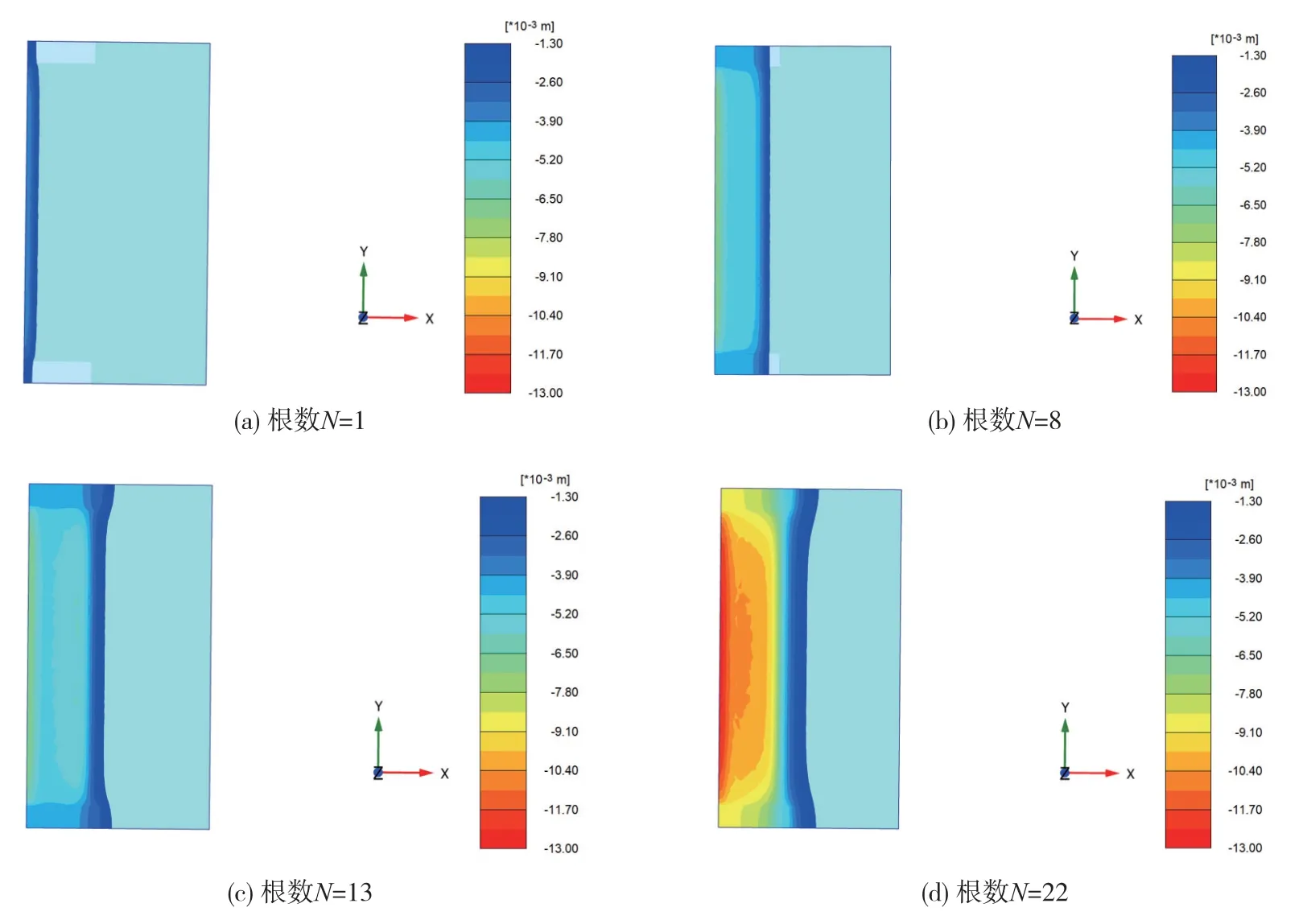
圖10 地表沉降云圖

由圖9 可知,當管幕頂進頂管根數分別為1 根、8 根、13 根、22 根時,對應的頂管周邊土體最大沉降值分別為4.57,7.22,7.33 mm 和12.85 mm,土體最大沉降出現在頂管中間(y=47 m)附近位置,頂管引起的地表變形軸向基本對稱。 隨著不斷推進,地表變形持續增加。 由圖10 可知,當第一根頂管頂入時,影響范圍很小,隨著頂進頂管根數的增加,地表沉降的影響范圍持續增大。

整體來看,由于頂管端頭的高壓旋噴加固和端部結構約束,呈現出端部沉降小,中間沉降大的變形特征,地表變形軸向基本對稱;地表沉降影響區域在管幕邊界(x=16.5 m)開始快速衰減。

5.2 橫向變形隨頂管變化規律

在地表最大沉降位置(y=47 m)處輸出地表沉降的橫剖線。 分別輸出第1 根、第8 根(上排16 根頂管完成)、第13 根(側排8 根頂管完成)和第22 根(44 根頂管全部完成)4 個計算階段的地表沉降曲線,見圖11。

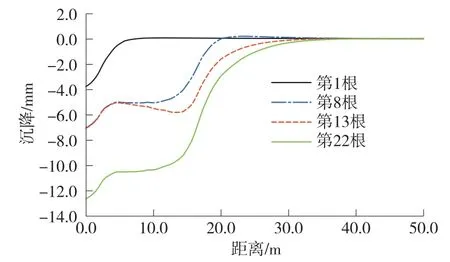
圖11 地表最大沉降位置橫向沉降曲線(y=47 m)

由圖11 可知,在頂入管幕上排中間第1 根頂管時,地表沉降最大值位于模型對稱邊界(x=0 m)位置,最大值為3.8 mm,影響范圍約6.1 m;在頂入管幕上排中間第8 根頂管(上排完成)時,地表沉降最大值增加到7.1 mm,影響范圍擴大到17.4 m,值得注意的是,x=5 m 至y=13 m 區間沉降值大小相近,形成沉降“平臺”。 其原因為,第1 根與第2 根與對稱的頂管(對稱邊界)之間有沉降疊加作用。 從第3 根頂管起,與對稱的頂管之間沉降疊加基本消失;在側排管幕頂入(第9 到13 根頂管)期間,對x=0 m 至x=5 m 的區域地表沉降基本無影響,沉降最大值無變化,此時沉降影響范圍邊界擴大到x=21 m。 因此,側排頂管影響范圍在x=5 m 至x=21 m 范圍。 在下排頂管完成時,地表沉降最大值增加到12.7 mm,影響范圍增加到24 m。

綜上所述,前兩根頂管引起x=0 m 至x=5 m 的區域范圍地表沉降疊加區,該區域沉降最大;第3 根到第8 根頂管頂進形成沉降平臺區,各頂管上方沉降值相近;側排頂管地表沉降影響范圍x=5 m 至x=21 m 區域,側排頂管不影響沉降疊加區最大沉降值;橫向地表沉降曲線類似于S 形,最終影響范圍x=24 m。

5.3 軸向變形隨頂管變化規律

在x=0 m 處,輸出軸向地表沉降曲線,分別輸出第1 根、第8 根、第13 根和第22 根4 個計算階段的地表沉降曲線,見圖12。

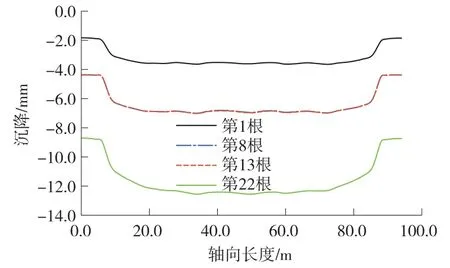
圖12 地表沉降軸向沉降曲線(x=0 m)

由圖12 可知,軸向沉降曲線形態為兩端小,中間大。 沉降從y=6 m 位置(加固土邊界)開始迅速增加,在y=20 m 位置開始趨于穩定,整體軸向形成盆狀沉降穩定區域,沉降穩定區域差異沉降較小。 從頂管施工進度來看,不同進度引起的地表軸向沉降形態基本一致,隨著進度沉降整體逐漸增大。 值得注意的是,側排4 根頂管的頂進未引起x=0 m 處軸向地表沉降曲線發生變化。

5.4 地層損失綜合分析

根據Peck 公式,最大沉降和土體損失量公式為

式中,Vlose為頂管單位長度的土體體積損失量;i為頂管中軸線到地面沉降曲線反彎點的水平距離,即地面沉降槽寬度系數;η為土體損失百分率;R為頂管半徑。 Peck 公式沉降曲線見圖13,其形態與圖12 中N=1 的曲線基本一致。

將第一根頂管的最大地表沉降量代入Peck 公式,有

根據數值模擬分析輸入條件和計算結果,計算第1 根樁頂入引起的地層實際損失率。Smax取3.8 mm,i取3.0 m,R取0.8 m,計算獲得實際地層損失為1.42%,數值模型中輸入的0.5%為鋼管收縮率,獲得地層實際損失率為1.42%的原因有以下兩點:①數值模型采用的對稱邊界,獲得沉降實際為2 根頂管的沉降,因而,Peck 公式獲得的收縮率實際為0.71%;②數值模擬輸入的收縮率為頂管結構的收縮體積,用于模擬周邊土體的應力釋放,在土體發生一定變形之后,剩余的土壓力作用到頂管上引起二次變形。

同理,可計算獲得44 根管幕頂管全部完成時的平均地層損失率。 根據管幕完全施工完成后的結果,最大沉降取12.8 mm,影響范圍反彎點i取17 m,R仍然取0.8 m,地層損失計算結果為0.60%。 可見平均頂管施工引起的地層損失率低于單根頂管,分析認為,管幕上排管土拱效應對下排頂管起到了保護作用。

綜上所述,采用數值仿真方法獲得的沉降曲線形態與Peck 公式沉降曲線基本一致。 數值模擬中采用鋼管收縮的方式獲得的沉降和影響范圍可以代入Peck 公式換算出地層損失率,數值模擬中輸入的收縮率(0.5%)較最終地層損失率(0.71%)小。 對比單頂管的地層損失率和密排管幕的地層損失率,發現后續頂管的施工引起的地層損失低于前期頂管的。 分析認為,管幕上排頂管土拱效應對下排頂管起到保護作用。

6 結論

(1)先施工完成上排頂管,施工下排頂管引起的沉降等值線被上排頂管干擾發生彎曲,在上排每兩根頂管的間隔位置形成“拱形”的沉降等值線,且上排頂管上方的階段位移明顯小于其下方的階段位移。 上排頂管形成的土拱效應對下排起到保護作用。 因此,密排管幕頂管群最佳的順序為:先施工管幕上排頂管,再施工管幕兩側及下排頂管。

(2)采用數值仿真方法獲得的沉降曲線形態與Peck 公式沉降曲線基本一致。 數值模擬中采用鋼管收縮的方式獲得的沉降和影響范圍可以代入Peck 公式換算出地層損失率,數值模擬中輸入的收縮率(0.5%)較最終地層損失率(0.71%)小。 對比單頂管的地層損失率和密排管幕的地層損失率,發現后續頂管的施工引起的地層損失低于前期。