多葉箔片氣體動壓軸承靜態特性研究
劉恒,賈晨輝,劉書明,李東東,張飛
(河南科技大學 機電工程學院,河南 洛陽 471003)
箔片氣體軸承具有無污染,自適應能力強,使用壽命長和運行穩定性良好等諸多優點,廣泛應用于低溫工程、國防和航空航天等領域,并發揮了重要作用[1-2]。箔片氣體軸承分為波箔型和多葉型(懸臂型)軸承等,多葉型軸承結構簡單,加工工藝要求低,廣泛應用在高速旋轉的小型輕載機械上。
文獻[3]通過引入輔助分析部件的方法,建立了含有大預緊效應的多葉箔片軸承的非線性接觸模型,并將其進行完全的氣彈耦合求解,結果表明此方法收斂性較好,并能很好地解決彈性箔片的非線性大變形扭曲和復雜載荷情況下的預緊問題。文獻[4-5]將多葉箔片軸承結構用到油潤滑箔片軸承中,搭建了針對多葉箔片軸承的試驗臺,對五葉片油潤滑的箔片軸承進行試驗,在轉速30×103r/min時軸承仍能穩定運轉,說明油潤滑箔片軸承在高速運行時表現良好,具有較好的抵抗沖擊能力以及良好的穩定性和適應能力。文獻[6]將多葉箔片油潤滑軸承的剛度引入到軸承轉子系統中,分析了軸承動態剛度對軸承轉子系統的影響,并搭建試驗臺驗證其結果,結果表明多葉箔片油潤滑軸承對轉子的升速適應能力強。文獻[7-9]提出一種帶彈性支持結構的油潤滑多葉箔片軸承,通過卡氏定理建立多葉箔片的變形模型對其進行求解,并搭建多葉箔片油潤滑軸承的試驗臺,試驗結果表明帶彈性支持結構的軸承承載力、穩定性都優于無彈性支持結構的軸承。文獻[10]通過試驗研究含波箔的四葉箔片軸承,提出一種確定剛度系數和阻尼系數的頻域識別方法。文獻[11-12]采用懸臂梁模型建立了考慮相鄰箔片面接觸的動力學模型,運用有限元法與加權余量法對雷諾方程進行耦合求解,并提出一種判斷相鄰箔片是否接觸的算法,但計算量大,會出現難收斂的問題,對網格劃分要求較高,而且未考慮預緊力對軸承性能的影響。隨著研究的深入,文獻[13]利用有限元法對新型三瓣式箔片軸承展開研究,分析了接觸面間庫倫摩擦力下預載和安裝角度對軸承靜動態性能的影響,發現預載能提高軸承的承載能力,且轉速越高承載能力越大。文獻[14]研究潤滑劑和熱蠕變對氣體軸承的影響,結果表明選擇摩爾質量大的氣體能提高軸承的穩定性和承載能力;相對于沒有熱蠕變的情況,有熱蠕變對氣體軸承的穩定性破壞明顯,但對承載能力有一定的提高。文獻[15]研究箔片厚度對波箔型氣體動壓軸承承載力的影響,結果表明箔片厚度與軸承承載力成反比。
文獻[4-9]針對多葉箔片油潤滑軸承進行研究,但未對箔片厚度、軸承間隙進行研究;文獻[11-12]未考慮預變形對多葉箔片氣體軸承性能的影響。軸承結構對多葉箔片氣體軸承性能影響的文獻較少,基于文獻[13-15]研究的軸承結構對波箔型氣體軸承性能的影響,本文針對有預變形的多葉箔片氣體動壓軸承,通過理論計算研究多葉箔片氣體動壓軸承靜態特性,分析軸承結構和運行參數對承載力的影響,為應用箔片氣體動壓軸承及優化其結構提供參考。
1 理論分析
如圖1所示,多葉箔片氣體動壓軸承由彈性支承和軸承座構成,彈性支承與轉子之間形成收斂楔。彈性支承由若干個箔片或箔片組件順次搭建構成,且箔片或箔片組件的一側通過插槽固定在軸承座上,箔片的另一側搭接在其他箔片上。在多葉箔片軸承工作過程中,軸承的氣膜壓力會導致箔片形狀發生變化,從而影響氣膜厚度,最終導致氣膜壓力的變化。

圖1 多葉箔片氣體動壓軸承實物圖
1.1 控制雷諾方程
多葉箔片氣體動壓軸承的氣膜間隙遠小于轉子半徑,可以把軸承沿周向展開建立坐標系,x為周向,z為軸向,y為氣膜厚度方向,如圖2所示。
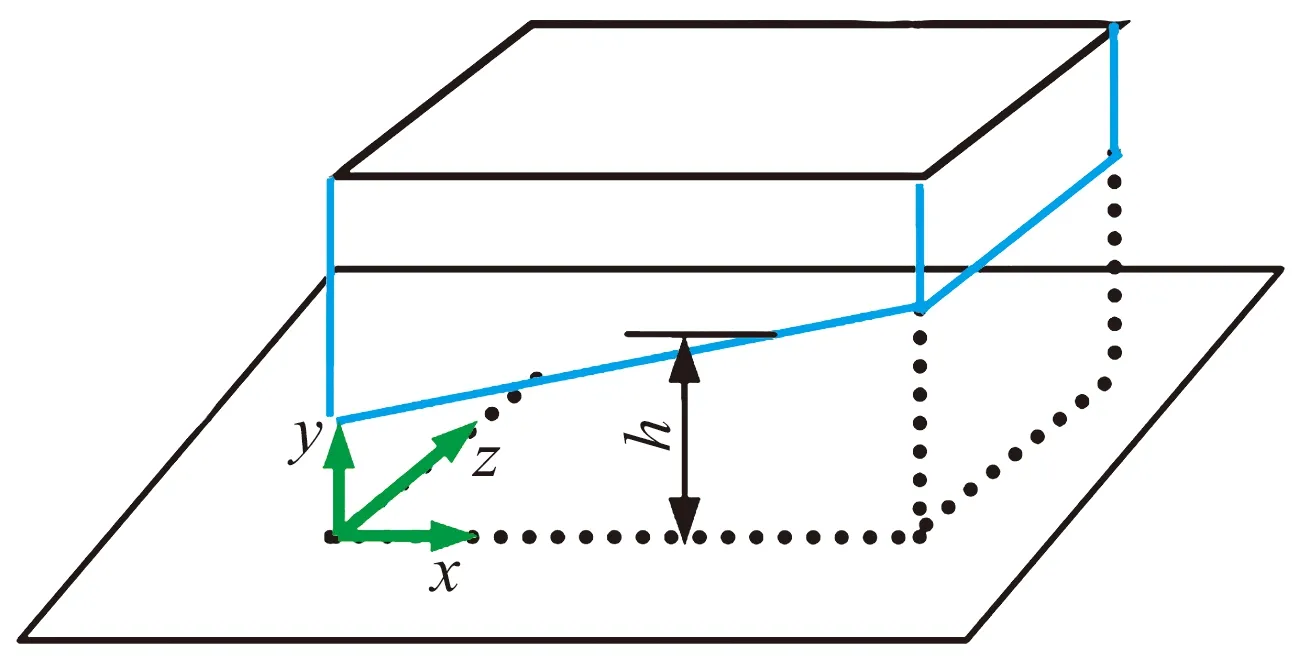
圖2 多葉箔片氣體動壓軸承氣膜展開圖
穩態時雷諾方程為
(1)
式中:p為氣體壓力;h為氣膜厚度;η為氣體動力黏度;R為轉子半徑;ω為軸徑角速度。
(2)
(3)
式中:L為軸承長度;p0為環境氣壓;C0為軸承半徑間隙;Λx為軸承數。
1.2 氣膜厚度模型
箔片裝配完成后假定箔片與箔片、轉子與箔片為線接觸且無作用力,在安裝前后箔片的曲率半徑保持不變,而且在裝配過程中箔片不變形。
多葉箔片的幾何關系如圖3所示,A為箔片內表面的末端點,B為轉子與箔片的接觸點,C為箔片內表面上任意一點,D為相鄰箔片接觸點,O為軸承中心,O′為箔片圓心。

圖3 多葉箔片的幾何關系
在不偏心時箔片與轉子相切,此時箔片沿周向均勻分布,可得如下關系
(4)
根據余弦定理,在△OO′D和△OO′A中可得到如下關系
(5)
式中:n為箔片數量;Rg為箔片曲率生成圓半徑;ρ0為箔片內表面曲率圓半徑;Ra為箔片內表面的末端點A構成的圓半徑;t為箔片厚度。
已知t,Rg,R,根據(4)—(5)式可計算Ra,α1,θ1的值。
根據余弦定理,在△OCO′中可得到如下關系
(6)

(7)
當箔片受預緊力影響時,箔片會發生變形,變形尺寸遠小于箔片尺寸,因此可按照徑向變形計算。箔片初始預變形采取懸臂梁模型如圖4所示。
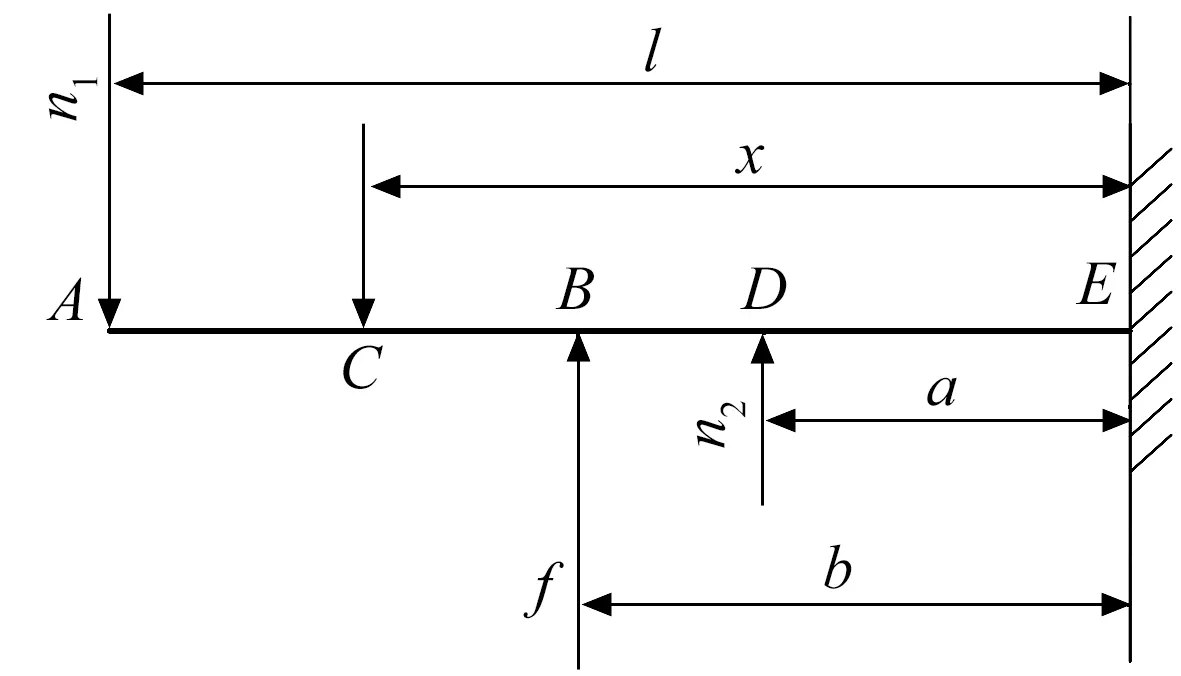
圖4 箔片懸臂梁示意圖
A點、B點和D點的變形分別表示為[16]
(8)
式中:n1,n2分別為單位寬度上A點、D點受到的接觸力;f為單位寬度上B點受到的預緊力;ΔB為箔片與轉子接觸點的初始預變形(ζ);ΔA和ΔD為該箔片與相鄰箔片的接觸點(接觸點在該箔片上)發生的變形;E為彈性模量;I為慣性矩。
由箔片對稱可得
ΔA=ΔD,
(9)
n1=n2。
(10)
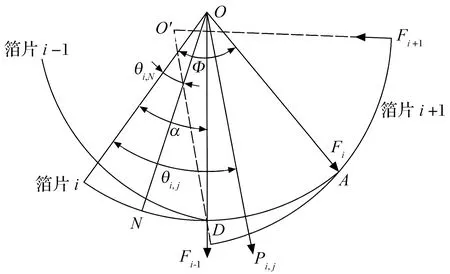
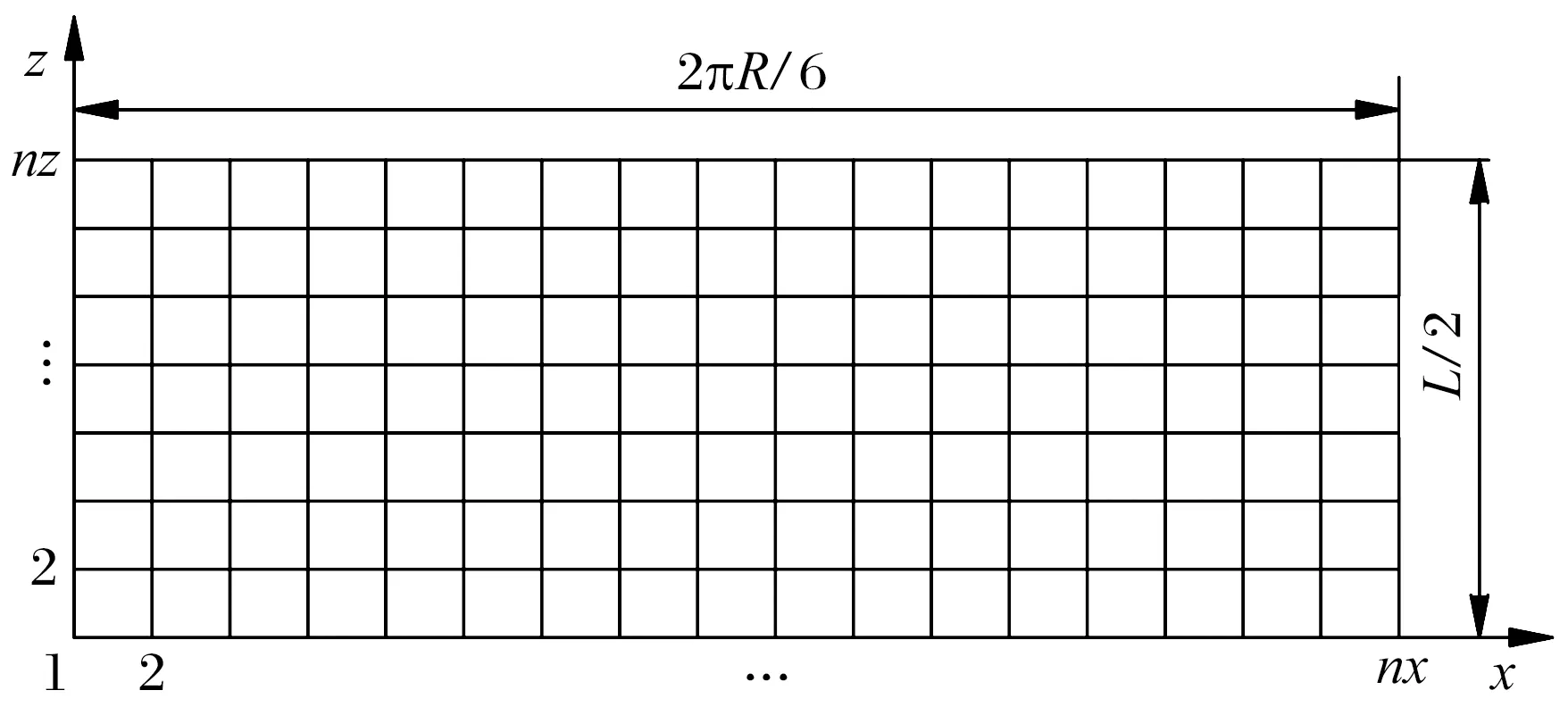
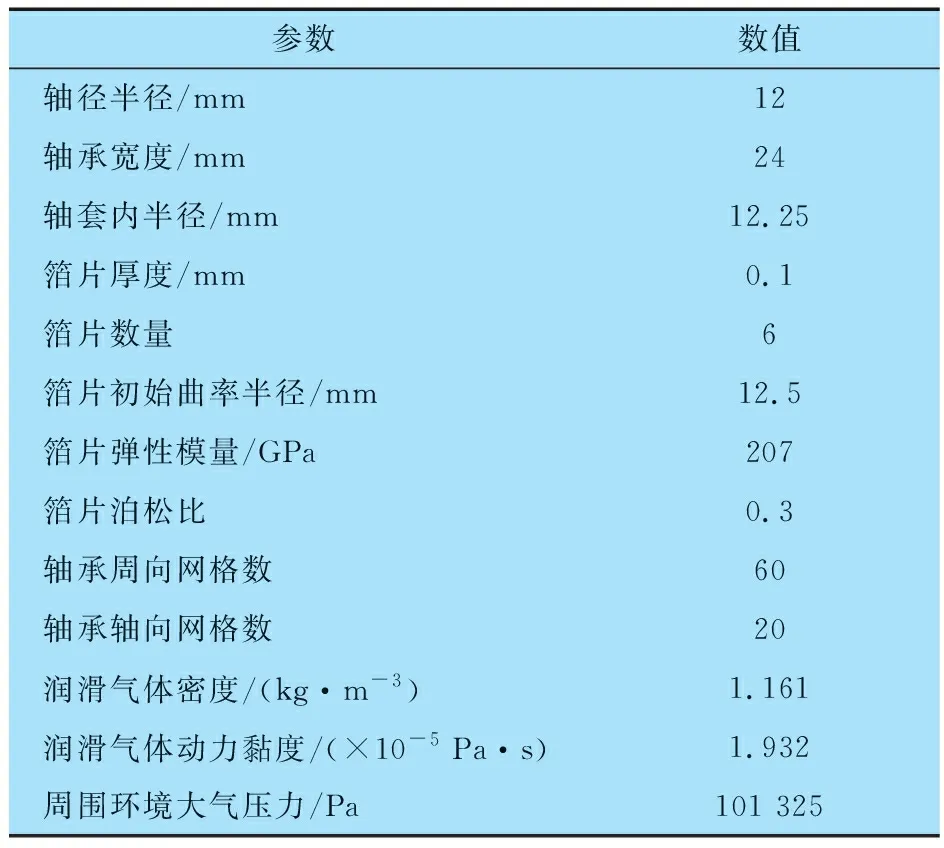
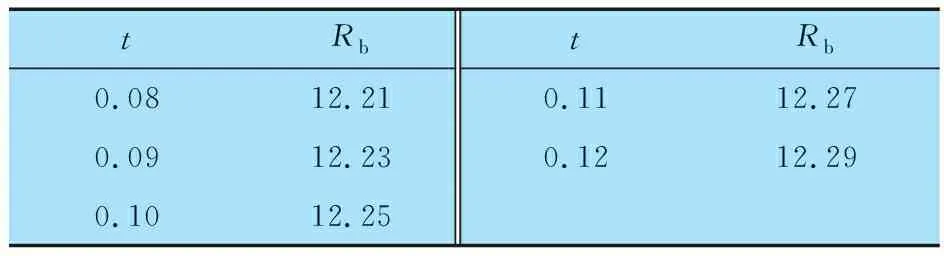
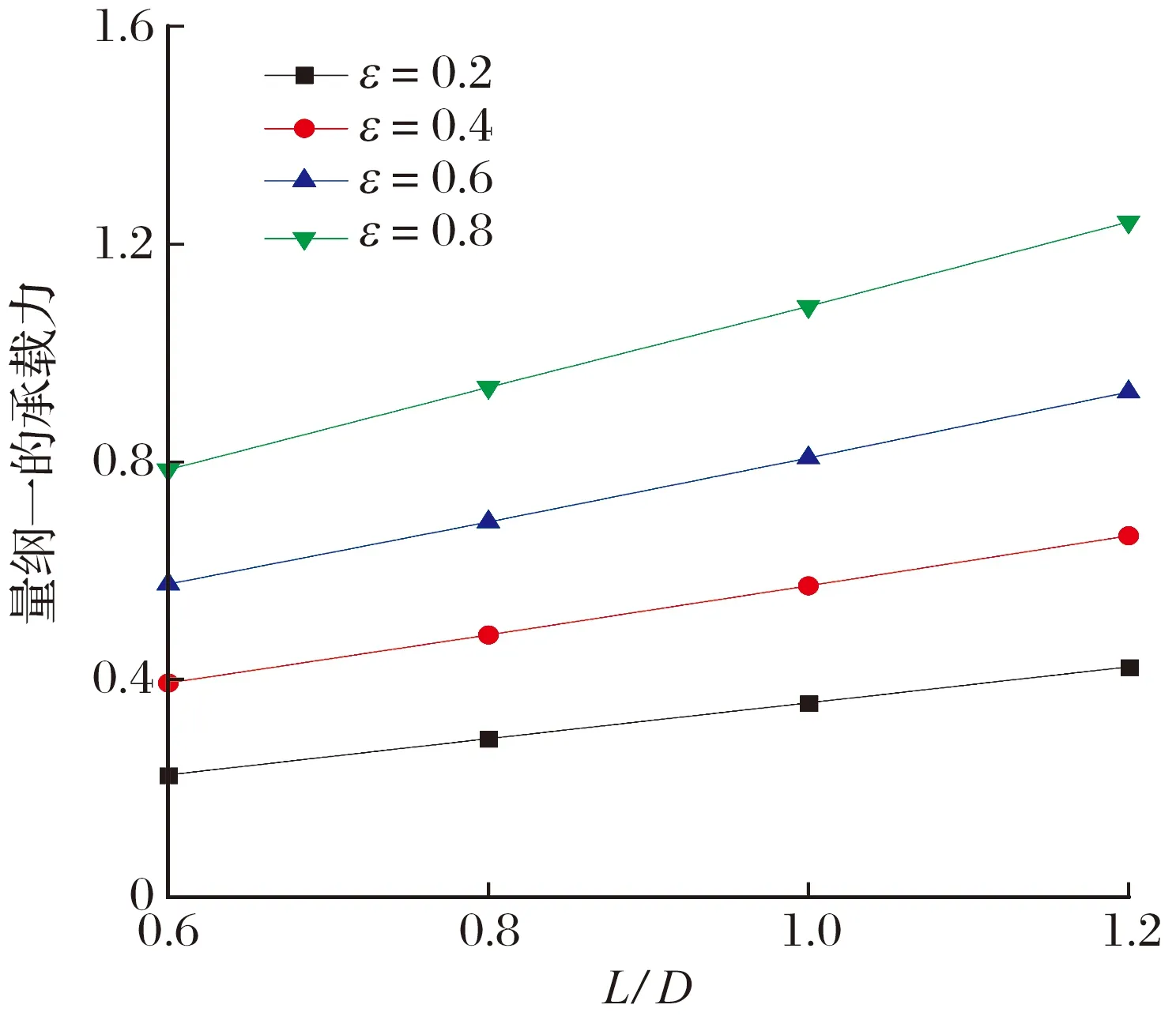
由 (8)—(10)式可求出f,則可求任意一點C的變形。當C點在B點與D點之間,即x (11) 當C點在A點與B點之間,即x≥b時 (12) 則初始氣膜厚度修正為 (13) 根據多葉箔片氣體動壓軸承結構,把箔片簡化為懸臂彎曲梁,并假定相鄰箔片之間無摩擦。因此,每個箔片只承受徑向力,在變形小的條件下,可利用卡氏定理計算箔片的變形。如圖5所示,當節點s受到單位法向力F作用時,節點u的徑向位移(柔度系數)U(K,Ψ)可表示為[12] 圖5 箔片變形圖 U(K,Ψ)= (14) 式中:K為節點u的圓心角;Ψ為節點s的圓心角。 將箔片簡化為懸臂彎曲梁,研究對象為箔片中任意一個箔片,其受力如圖6所示。箔片i的受力狀態為箔片i-1的接觸力Fi-1、箔片i+1的接觸力Fi+1以及箔片i上節點j受到的氣膜力Pi,j。Φ為箔片的包角,θi,N為任一點N和O點連線與箔片固定端的夾角,α為箔片重疊區的角度,θi,j為氣膜力Pi,j與固定端的夾角。 圖6 箔片受力圖 兩箔片的接觸點A在箔片i上的徑向位移為 FiU(Φ,Φ), (15) 同理接觸點A在箔片i+1上的徑向位移為 Fi+1U(α,Φ), (16) 由于箔片i與箔片i+1在A點接觸,所以 δi,A=δi+1,A, (17) 化簡可得 -Fi-1U(Φ,α)+Fi[U(α,α)+U(Φ,Φ)]- (18) 本文研究的多葉箔片氣體動壓軸承有6個箔片,按照i=2→6→1的順序書寫矩陣,即 AF=PU, (19) F=[F1F2F3F4F5F6]T, 式中:A,U為柔度矩陣;F為節點接觸力矩陣;P為氣膜壓力矩陣。 由(19)式求出箔片間的作用力,即可得到整個箔片的受力狀態,進而得到箔片所有點變形的大小,選擇箔片i為研究對象,則任意點N的位移為 δi,N=-Fi-1U(θi,N,Φ)+FiU(θi,N,α)- (20) 軸承正常運行時氣膜厚度由轉子的偏心量、氣膜厚度的初始量以及箔片變形量構成,則氣膜厚度為 h=h0+ecos(θ-φ0)+uf, (21) 式中:h0為初始氣膜厚度;e為偏心量;θ為氣膜圓周方向坐標;φ0為偏位角;uf為箔片的變形量。 將牛頓-拉弗森迭代公式代入(3)式中并化簡得 (22) 各階中心差分得 整理得 Ai,jδi-1,j+Bi,jδi+1,j+Ci,jδi,j-1+Di,jδi,j-1+ Ei,jδi+1,j=-Fi,j, (23) 多葉箔片氣體動壓軸承每個箔片的邊界條件都相同,可先通過單獨求解每個箔片,然后通過整體組裝計算軸承的靜態特性。對箔片進行網格劃分,如圖7所示。 圖7 箔片的網格劃分 軸承軸向兩端與大氣相通,且軸承相鄰箔片搭建處最小氣膜厚度遠小于箔片厚度,所以可將箔片搭建處和軸承軸向兩端的壓力等同于大氣壓力。則環境邊界條件為 p=p0, (24) 計算區域取軸向的一半,則氣壓變化梯度在中間軸面時為零,則對稱邊界條件為 (25) 收斂條件為 (26) 氣壓分布會引起箔片變形,箔片變形會改變膜厚的分布,進而改變氣壓分布,將氣壓分布和箔片變形不斷進行迭代求解,當滿足收斂條件時,計算停止。數值計算流程如圖8所示。 為確定計算以及程序編寫的準確性,采用本文方法計算不考慮預緊力以及預緊力為0.1 Pa時文獻[17]中多葉箔片氣體動壓軸承的承載力,結果如圖9所示:當不考慮預緊力時,本文理論計算的承載力與文獻計算的基本一致,驗證了本文方法的正確性以及程序編寫無誤。在預緊力為0.1 Pa時,軸承承載力比無預緊的大,因為預緊力會使箔片在軸承工作前發生變形,承載力會有所增大,與實際一致。因此本文計算模型正確。 圖9 本文與文獻[17]軸承承載力的計算結果對比 本文計算的多葉箔片氣體動壓軸承的結構和其他參數見表1。 表1 多葉箔片氣體動壓軸承結構和其他參數 當偏心率ε為0.2,轉速n為40×103r/min時,多葉箔片氣體動壓軸承氣膜壓力和氣膜厚度的分布如圖10所示: 氣膜壓力和氣膜厚度中出現了6個明顯的波谷和波峰,且箔片3和箔片4壓力明顯大于其余箔片的,這主要是由于偏心的作用,軸承主要承載區在箔片3和箔片4處,且對應的氣膜厚度最小。 圖10 量綱一的氣膜壓力和氣膜厚度 轉速和偏心率對軸承承載力的影響如圖11所示,當偏心率不斷增大時,承載力也將增大,且轉速越高承載力越大。這是由于轉速升高會導致氣體流速變快,進而增強了軸承的氣體動壓效應,氣膜壓力變大,所以承載力增大。 圖11 轉速和偏心率對軸承承載力的影響 當偏心率不變時,若使軸承結構的幾何尺寸不變,僅箔片厚度變化,相當于對軸承預緊。因此本文保持軸承結構的幾何尺寸不變,讓箔片厚度與軸套內半徑Rb對應變化,具體見表2。 表2 箔片厚度與軸套內半徑的對應關系 箔片厚度對軸承承載力的影響如圖12所示,當偏心率為0.2和0.4時,承載力隨箔片厚度的增大而增大,且箔片厚度超過0.10 mm時,承載力的增大量越來越小,這是因為當箔片厚度增大時,箔片剛度將會增大,有利于承載;當偏心率超過0.6時,隨著箔片厚度逐漸增大,承載力呈先增大后基本不變或減小的趨勢,且拐點在箔片厚度為0.10 mm時,這是因為箔片厚度增大導致軸承氣膜厚度增大,進而使承載力減小。由計算結果可知,箔片厚度選取0.10 mm,有利于軸承承載。 圖12 箔片厚度對軸承承載力的影響 綜上所述,箔片厚度增大的同時使箔片支承剛度和氣膜厚度增大,這2種效果的共同作用影響承載力大小。當偏心率為0.2和0.4時,箔片厚度增大使支承剛度變大占主導;當偏心率超過0.6時,箔片厚度增大使氣膜厚度增大占主導。 轉子直徑D為定值,通過改變軸承長度L使長徑比L/D為0.5~1.2。長徑比對軸承承載力的影響如圖13所示,當偏心率不變時,隨著軸承長徑比的不斷增大,承載力也會增大。這是由于當軸承的長徑比不斷增大時,有效的軸承承載區域會變大,會使承載力增大。但長徑比增大對提高承載力的作用較小,當長徑比從0.6增大至1.2,即長徑比增大1倍時,承載力將提高0.5倍左右。 圖13 長徑比對軸承承載力的影響 保持軸承其他結構不變,軸承間隙C的大小僅由軸套內半徑決定(C=Rb-R-2t),具體見表3。 表3 軸承間隙與軸套內半徑的對應關系 軸承間隙對軸承承載力的影響如圖14所示:當偏心率不變時,隨著軸承間隙的不斷增大,軸承承載力減小,這是因為當軸承間隙增大時,氣膜厚度增大,進而使動壓效應減弱,承載力減小;當偏心率為0.8,軸承間隙從0.05 mm增大到0.06 mm時,承載力減小40%,軸承間隙從0.07 mm增大到0.08 mm時,承載力減小28%。說明多葉箔片軸承的間隙越小,越有利于軸承動壓效應的產生。因此可通過減小軸承間隙來增大軸承的承載力,但軸承間隙減小時,會導致軸承啟停時摩擦增大,進而影響軸承壽命。 圖14 軸承間隙對軸承承載力的影響 軸承預變形對軸承承載力的影響如圖15所示: 當偏心率不變時,軸承預變形可使其承載力增大,且隨偏心率不斷增加時,預變形越大承載力的差值越大。這是由于軸承在預緊時會使箔片在軸承工作前發生變形,有利于提高箔片的剛度。 圖15 軸承預變形對軸承承載力的影響 建立了箔片含有預變形的多葉箔片氣體動壓軸承計算模型,采用牛頓-拉弗森迭代法以及有限差分法對雷諾方程和氣膜厚度方程進行求解,研究轉速、偏心率、箔片厚度、長徑比、軸承間隙以及預變形對軸承承載力的影響,得到以下結論: 1)隨著偏心率的不斷增大,軸承承載力不斷增大,且轉速越高承載力越大;偏心率相同時,隨著軸承長徑比的不斷增大,承載力不斷增大,但增幅不明顯。 2)當偏心率小于0.6時,軸承承載力隨箔片厚度增大而增大;當偏心率大于0.6時,軸承承載力拐點出現在箔片厚度為0.10 mm處,此時承載力最大。 3)可通過減小軸承間隙提高軸承承載力,但軸承間隙小時啟停摩擦會增大,影響軸承壽命,應慎重選擇;當偏心率相同時,預變形越大越有利于提高軸承承載能力。
1.3 離散雷諾方程

1.4 網格劃分及邊界條件
1.5 計算流程
2 計算程序驗證

3 結果分析
3.1 多葉箔片氣體動壓軸承氣膜壓力的分布

3.2 轉速和偏心率的影響

3.3 箔片厚度的影響
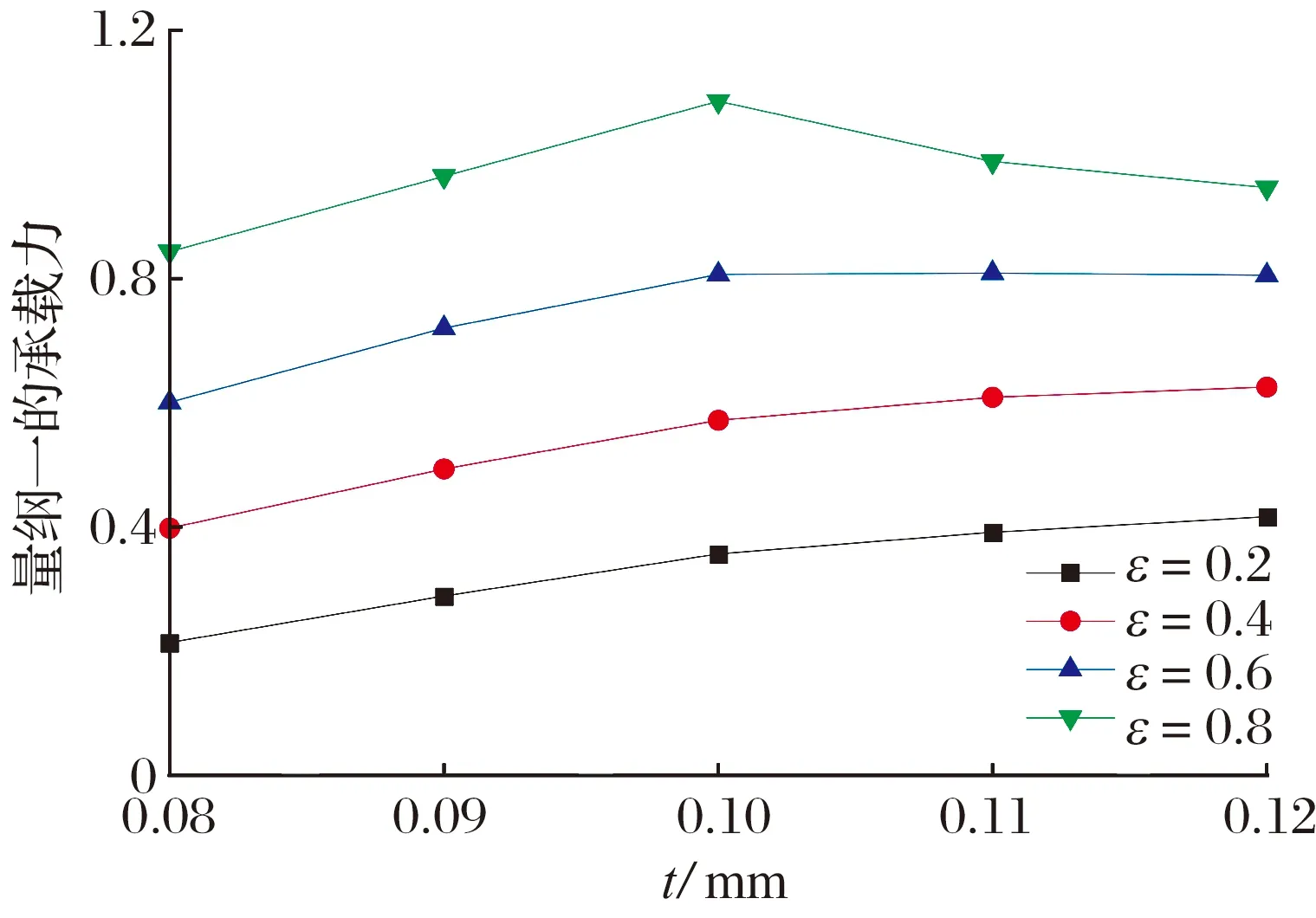
3.4 長徑比的影響
3.5 軸承間隙的影響


3.6 軸承預變形的影響

4 結論

