微型稀薄氣體潤滑多葉軸承的靜態性能分析

吳垚,郗文君,張彩麗,劉言松,曹巨江

(1.陜西科技大學 機電工程學院,西安 710021;2.施耐德(西安)創新技術有限公司 低壓事業部,西安 710075)

隨著超精密加工技術的不斷革新,航空航天、國防軍工、電力能源和低溫制冷等領域的機械設備向著微型化、高精度、多功能、低能耗以及智能化等方向快速發展,使微型渦輪發動機、微型燃氣輪機和微型渦輪增壓器等微型透平旋轉機械實現了各種能量間的轉換,能源效率提升和微量動力輸出[1-2]。微型氣體軸承具有結構簡單、氣體介質性能穩定、回轉精度高、摩擦功耗小及工作溫度范圍寬等優點,是微型轉子的最佳支承形式[3]。微型多葉氣體軸承的瓦間溝槽具有防止壓力擾動擴散、削弱氣膜交叉剛度和收集雜質粒子的作用,各周向槽視為一個“氣泵”,可增加潤滑膜厚和質量流量,減小軸頸-軸瓦表面的接觸概率[4-5]。隨著軸頸與軸瓦之間特征尺寸的減小,潤滑氣膜厚度接近或小于氣體分子平均自由程時,微小間隙內稀薄氣體流動問題與宏觀尺度下的流動特性明顯不同,必須考慮稀薄效應對微型多葉氣體軸承性能的影響[6]。

目前,許多學者提出了不同的氣體稀薄效應模型修正可壓縮雷諾方程,研究了稀薄效應對超薄氣膜潤滑性能的影響。如1階滑移模型[7]、2階滑移模型[8]、1.5階滑移模型[9]、 FK模型[10-11]及適用于任意克努森數的新滑移模型[12]等。文獻[13-14]分析了稀薄效應對磁頭/磁盤系統納米薄膜潤滑特性的影響,提出大軸承數和含有壓力的剪切流項的可壓縮雷諾方程的有限差分法。文獻[15]利用分形函數表征微型氣體軸承表面粗糙度,指出在偏心率和軸頸轉速較高時軸承承載力的隨機波動明顯。文獻[16]采用有限差分法和控制體積法求解了1階速度滑移和溫度階躍邊界條件的動量方程和能量方程,給出微小圓通道內層流的瞬態傳熱機理。文獻[17]比較了連續模型、1階滑移模型和新滑移模型對微型三瓦可傾瓦氣體軸承各瓦塊壓力和承載力的影響,發現克努森數較大時,1階滑移模型計算的承載力明顯大于新滑移模型。

國內外在多葉滑動軸承潤滑理論方面也取得了重要進展:文獻[18]運用施圖姆-劉維爾(Sturm-Liouville)理論和分離變量法,提出一種求解軸向槽徑向滑動軸承非線性油膜力的近似解析模型;文獻[19]通過影響系數法計算軸瓦彈性變形,研究了微溝槽水潤滑軸承的彈流潤滑性能,結果表明合適的溝槽深度在偏心率較小時可改善軸承潤滑性能;文獻[20]基于窄溝槽理論建立了人字槽氣體軸承非線性行為的預測模型;文獻[21]利用伽遼金有限元法分析了光滑、部分織構和完全織構表面對雙瓣徑向滑動軸承性能的影響,結果表明在壓力形成區域有表面織構且溝槽長徑比為1時會顯著提高軸承的動力穩定性。

綜上所述,現有微型氣體軸承潤滑性能的研究主要是針對圓柱氣體軸承,有關微型多葉氣體軸承靜動態特性的理論還需要深入研究。本文采用茲曼稀薄效應模型修正氣體潤滑雷諾方程,推導考慮氣體稀薄效應時微型多葉氣體軸承靜態性能的有限差分法,詳細討論瓦塊分布位置和軸承參數對氣膜壓力、承載力和摩擦因數的影響,為微型旋轉機械的性能預測和結構優化提供理論依據和技術支承。

1 微型多葉氣體軸承結構及分析模型

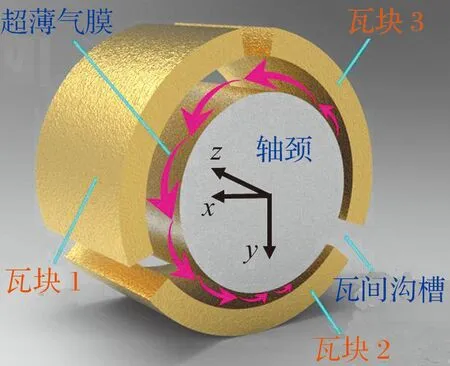
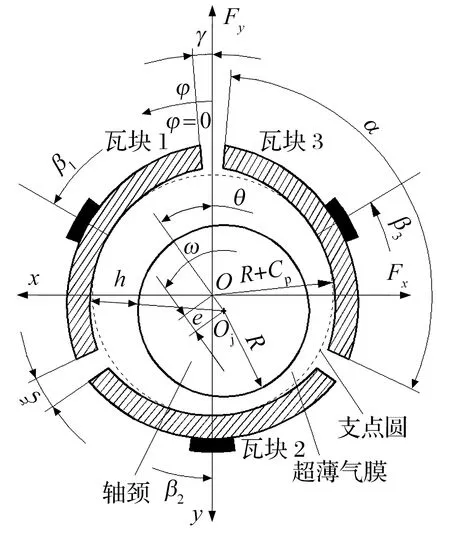
微型多葉氣體軸承一般由多個瓦塊組成,最常見的是三葉氣體軸承,瓦上承載和瓦間承載微型三葉氣體軸承的模型和結構示意圖分別如圖1、圖2所示,瓦上承載軸承的主要承載區位于底部第2個瓦塊的中間截面處,而瓦間承載軸承的軸頸重量由下方2個瓦塊共同支承。圖中:O為軸承中心,Oj為軸頸中心;θ為偏位角,α為每個瓦塊的瓦包角,ξ為軸向槽的槽寬包角,γ為軸承上方豎直線到第1個瓦塊進氣邊的位置角,β為瓦塊中間位置角,φ為從y軸負方向逆時針開始計算的氣膜位置角;e為軸頸中心相對軸承中心的偏心距,R為軸頸半徑,h為軸頸與瓦塊間的氣膜厚度,ω為軸頸轉動角速度,Fx,Fy分別為軸承在水平、豎直方向的氣膜合力。各瓦塊內表面與軸頸表面在軸頸旋轉方向上形成超薄氣膜, 與微型圓柱氣體軸承相比,微型多葉氣體軸承有2個間隙:半徑間隙Cb(瓦塊內圓弧半徑與軸頸半徑之差)和裝配間隙Cp(瓦塊支點圓與軸頸半徑之差)。

(a) 瓦上承載

(a) 瓦上承載

由于黏性作用,軸頸旋轉帶動稀薄氣體在微型多葉氣體軸承表面形成超薄潤滑氣膜,從而為轉子提供必要的支承。忽略潤滑膜的慣性效應和熱效應且假設稀薄氣流為層流,根據納維埃-斯托斯流體運動方程和連續性方程,結合牛頓黏性定律、雷諾假設并考慮稀薄效應的影響, 基于茲曼方程修正的超薄氣膜潤滑量綱一的雷諾方程為

(1)

P=p/pa,H=h/Cb,φ=x/R,η=z/R,

Kn=λ0/h,

式中:P為量綱一的氣膜壓力;p為氣膜壓力;pa為環境氣體壓力;H為量綱一的氣膜厚度;h為氣膜厚度;φ,η分別為量綱一的周向和軸向坐標;Λ為軸承數;μ為稀薄氣體黏度;Q為考慮氣體稀薄效應的Poiseuille流量比,即氣體稀薄效應的修正系數[22];Kn為克努森數;λ0為氣體平均分子自由程,取65 nm。

忽略瓦塊厚度,微型多葉氣體軸承各瓦塊任一點量綱一的氣膜厚度為

H=1+εcos(φ-θ)-mpcos(β-θ),

(2)

ε=e/Cb,

mp=1-Cp/Cb,

基于單片機的多功能視力保護器設 計 ……………………………………………………… 梁東麗，劉 穎（21）

式中:ε為軸頸中心相對軸承中心的偏心率;mp為預載荷系數。

相應的稀薄氣體潤滑方程量綱一的壓力邊界條件為

(3)

式中:L為軸承長度;φ0為從角起線到瓦塊進氣邊的角度;φ1為從角起線到瓦塊出氣邊的角度。

2 修正雷諾方程的有限差分解法

為快速求解超薄氣膜潤滑修正雷諾方程,將(1)式進行數學變換[23],令

(4)

則

(5)

求解微型多葉氣體軸承的靜態特性必須得到氣膜壓力分布,(5)式是二維非線性偏微分方程,傳統解析法求解非常困難,本文利用有限差分法和連續超松弛法求解,將各瓦塊內超薄氣膜網格劃分,每個節點處的壓力值作為各階差商的數據,通過求解所有節點處的壓力值近似獲得氣膜壓力分布情況。

氣膜網格劃分如圖3所示,沿周向φ和軸向η分別均勻劃分k和l格,網格間距Δφ=2π/k,Δη=2π/l;i,j分別為周向和軸向的網格節點編號;i=1,2,…,k+1;j=1,2,…,l+1。

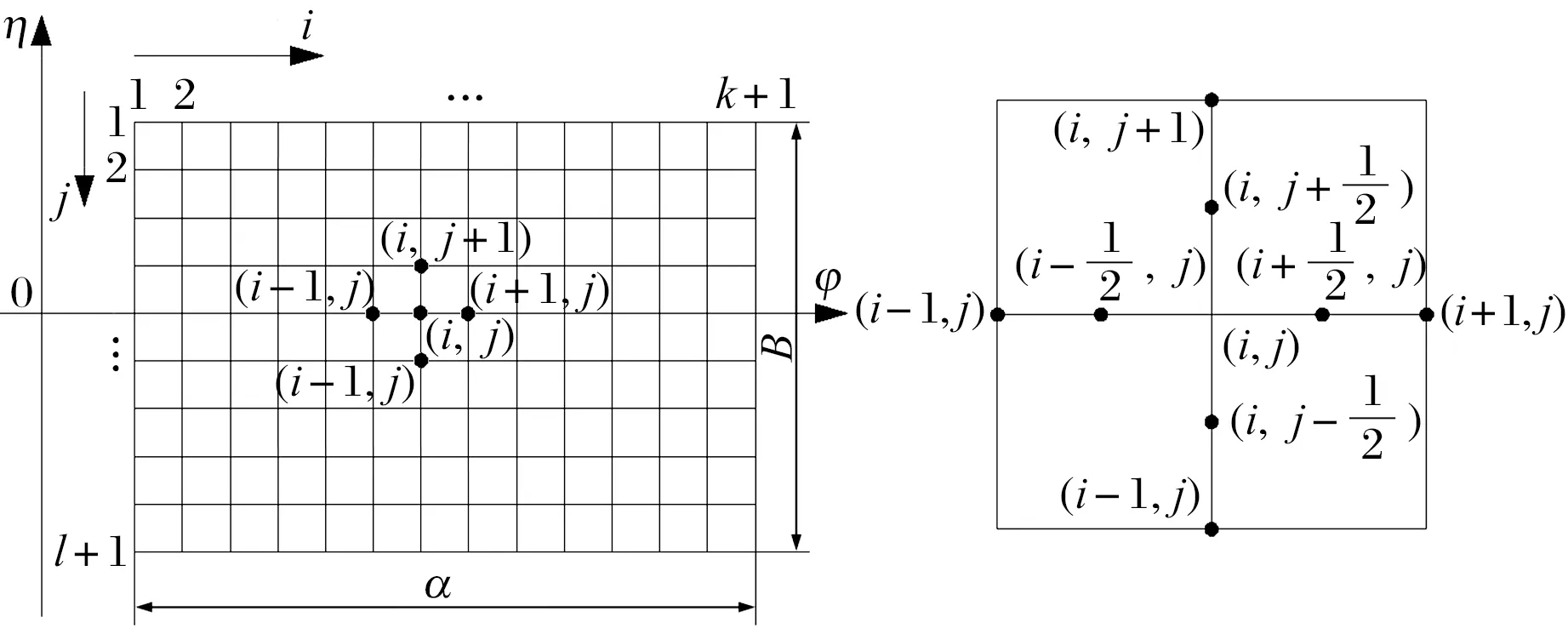
圖3 微型多葉氣體軸承氣膜網格劃分

將(5)式進行中心和向前差分離散可得(6)式,將(6)式移項、合并同類項后變為Ai,jΠi+1,j+Bi,jΠi-1,j+Ci,jΠi,j+1+Di,jΠi,j-1-Ei,jΠi,j=Fi,j的形式,即

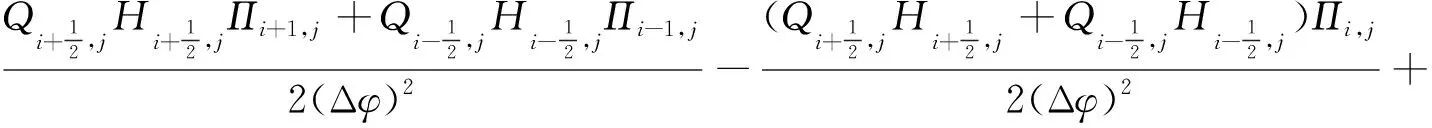
(6)

Λ(Si+1,j-Si-1,j)Δφ。

(7)

根據超松弛迭代公式求解上述方程組得到各瓦塊量綱一的氣膜壓力分布。耦合計算氣膜厚度及壓力分布過程中稀薄效應的修正系數與氣膜厚度緊密相關,需要同時不斷循環更新Poiseuille流量比的結果,微型多葉氣體軸承靜態性能計算的基本流程如圖4所示。當迭代計算氣膜壓力滿足(8)式收斂準則即終止迭代過程,相對誤差δ取1.0×10-6。

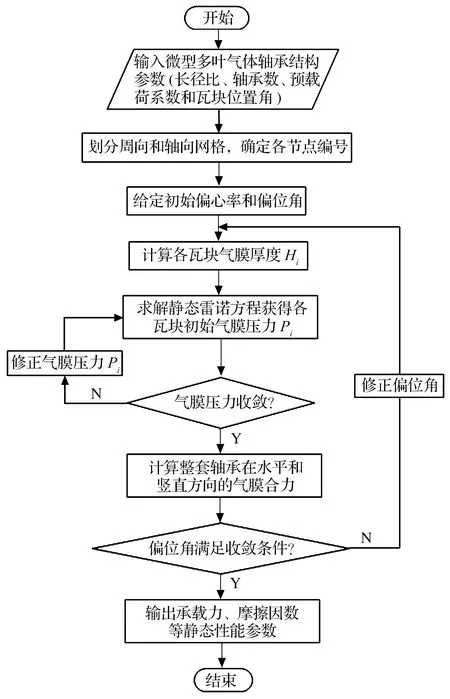
圖4 微型多葉氣體軸承靜態性能計算的基本流程圖

(8)

微型多葉氣體軸承的靜態性能由各部分圓弧瓦塊共同決定,其在水平和豎直方向的氣膜力為

(9)

則偏位角θ、量綱一的承載力CL和摩擦因數μb分別為

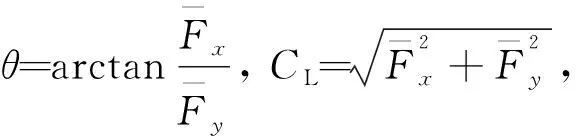
3 結果與討論

為驗證上述微型多葉氣體軸承靜態性能計算方法和自編程序的正確性,給出了長徑比L/D=0.5,mp=0,Λ=0.5,α=115°,γ=38.9°時本文與文獻[24]有關軸向槽氣體軸承量綱一的承載力和偏位角的結果(表1),其中ε′為軸頸中心相對支點圓中心的偏心率(ε′=e/Cp)。文獻[24]采用MATLAB中的PDE工具箱求解氣體潤滑雷諾方程。由表1可知,相同結構參數和運行參數下2種方法的結果非常接近,誤差均在2.5%以內,驗證了該算法的準確性和程序的可靠性。

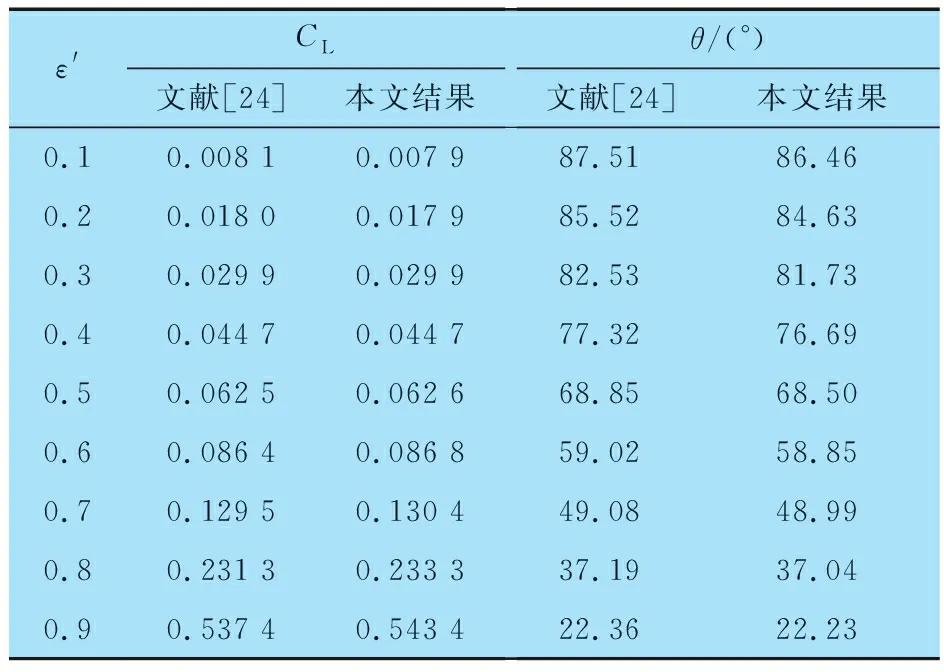
表1 本文計算的承載力和偏位角與文獻[24]的數值結果對比

本文選取微型多葉氣體軸承的結構參數如下:半徑間隙Cb為1 μm,瓦塊的瓦包角α為100°,瓦上承載和瓦間承載的γ分別為-10°和50°,氣體動力黏度為1.8×10-5Pa·s,環境壓力pa為1.013×105Pa。

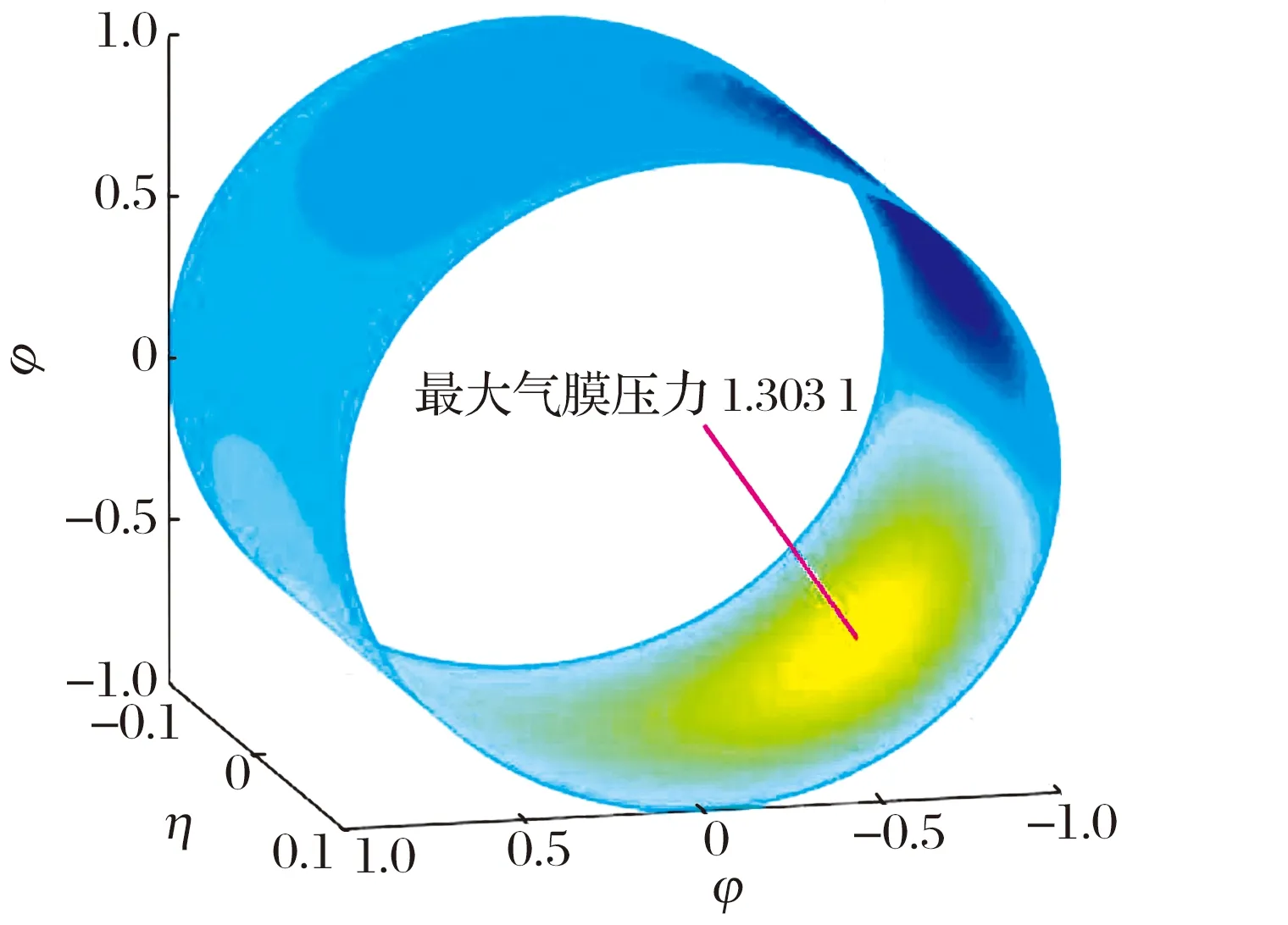
當ε′=0.6,L/D=0.1,mp=0.5,軸頸轉速N為4×105r/min時,軸承的氣膜壓力分布如圖5所示:預載荷系數較大時,微型多葉氣體軸承的最大氣膜壓力高于相同結構參數的微型圓柱氣體軸承,這是因為預載荷系數越大,瓦塊內圓弧半徑與軸頸半徑的差值(裝配間隙Cp)越小,相應的超薄氣膜厚度也越小;瓦間承載微型多葉氣體軸承的局部氣膜壓力最大,說明氣膜壓力峰值附近的瓦間溝槽吸入外部氣體提高了潤滑劑流量,很大程度降低了氣體稀薄程度,從而提高了軸承的整體氣膜壓力。因此,微型多葉氣體軸承可作為微型高速轉子的有效支承。

(a) 微型圓柱氣體軸承

當ε′=0.6,L/D=0.1時,軸頸轉速和預載荷系數對軸承承載力的影響如圖6所示:隨著軸頸轉速增大,承載力均近似呈線性增加的趨勢,這是因為軸頸轉速增加強化了軸承的動壓效應,稀薄氣流隨轉子高速旋轉密度增大, 其稀薄程度有所降低;預載荷系數越大,微型多葉氣體軸承的承載能力越強且承載力偏差越明顯;當mp=0.5時,微型多葉氣體軸承的承載力大于相同結構參數的微型圓柱氣體軸承,說明預載荷系數較大時,微型多葉氣體軸承可克服微型圓柱氣體軸承承載力較大但穩定性差的缺點,滿足微納米尺度加工裝配和超高速可靠運轉的要求;瓦上承載微型多葉氣體軸承的承載力比瓦間承載時的大,這是由于瓦上承載時的瓦塊有效承載面積更大,連續性超薄氣膜的范圍較寬。

當ε′=0.6,L/D=0.1時,軸頸轉速和預載荷系數對軸承偏位角以及摩擦因數的影響如圖7所示:偏位角隨軸頸轉速的增大而逐漸減小,意味著軸承與轉子在豎直方向的偏移量減小,有利于提升軸承的運轉穩定性;預載荷系數越大,偏位角降幅越顯著,瓦間承載時的偏位角明顯小于瓦上承載時;摩擦因數隨著軸頸轉速的增大而線性增大,當mp=0.3和0.5時,微型多葉氣體軸承的摩擦因數大于微型圓柱氣體軸承,這是因為瓦塊支點圓半徑減小, 支點圓中心與軸承幾何中心位置的不重合度增加,轉子高速旋轉導致的稀薄氣流黏性剪切力增強;瓦間承載時的摩擦因數略高于瓦上承載時,這是因為軸向溝槽的“泵吸效應”增大了稀薄氣體的流量,加劇了超薄氣膜與軸頸表面的相互作用。

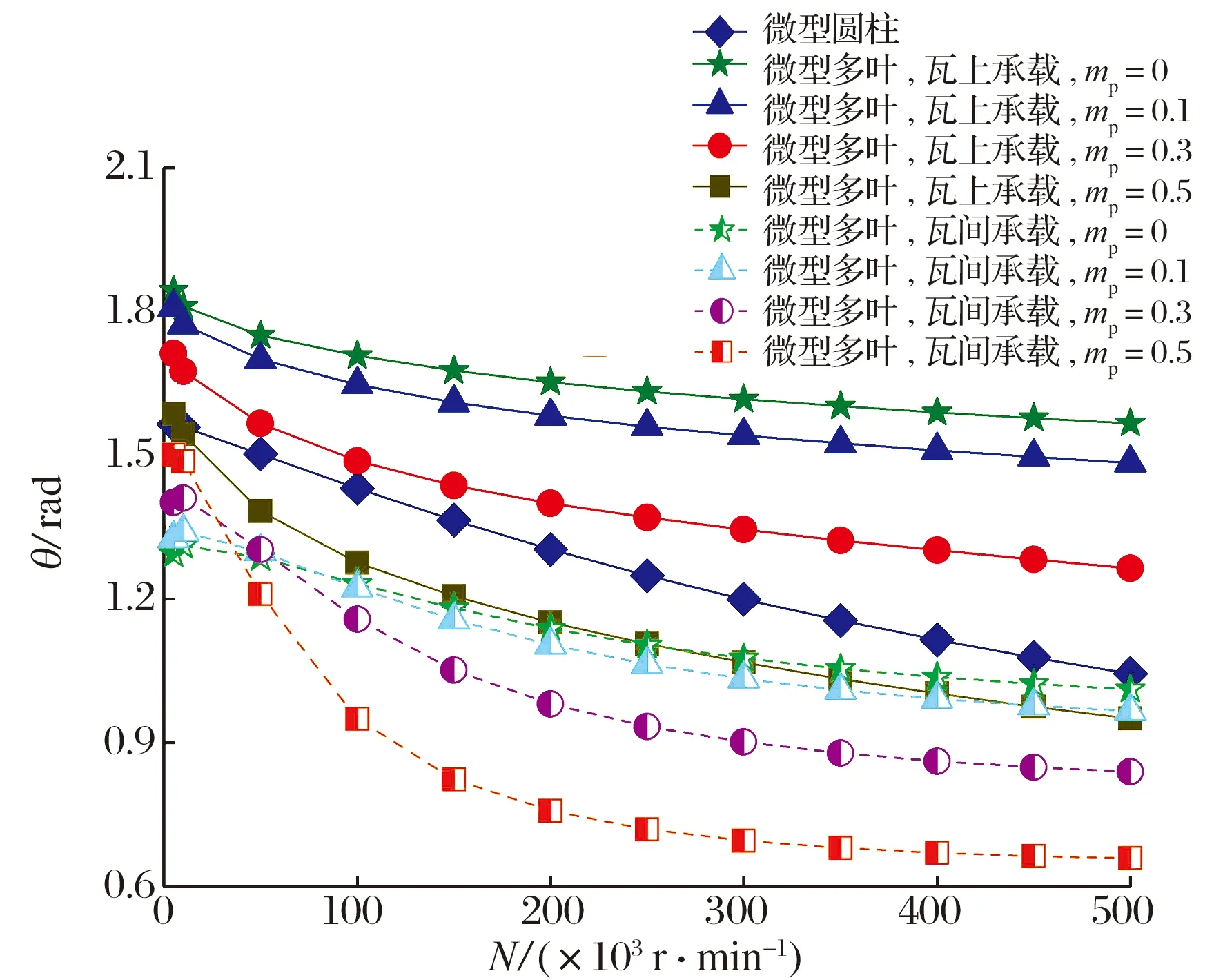
圖7 軸頸轉速和預載荷系數對軸承偏位角和摩擦因數的影響

當Λ=12,ε′=0.5時,長徑比和預載荷系數對軸承承載力和摩擦因數的影響如圖8所示:承載力均隨長徑比的增加而增加,長徑比較小時,預載荷系數和瓦塊分布位置的計算結果區別不大,而當L/D>0.4時,微型圓柱氣體軸承的承載能力遠高于微型多葉氣體軸承,且隨長徑比增加,2種軸承的承載能力差距更明顯,這是因為長徑比增加對應軸承長度增大,瓦間溝槽破壞氣膜連續性的弊端開始顯現,動壓效應減弱;由于超精密加工和硅片厚度的限制, 真實硅基微型氣體動壓軸承的長徑比比傳統氣體軸承小1個數量級,通常為0.05～0.10,這表明長徑比不是影響微型氣體軸承潤滑性能的主要結構參數;與軸頸轉速對承載力的影響類似,相同長徑比條件下,承載力隨預載荷系數的增加而增大,瓦上承載時承載力更大;摩擦因數隨長徑比的增加而線性增加,預載荷系數較大時, 微型多葉氣體軸承的摩擦因數高于微型氣體圓柱軸承,而預載荷系數較小時,瓦塊分布位置幾乎對摩擦因數沒有影響。

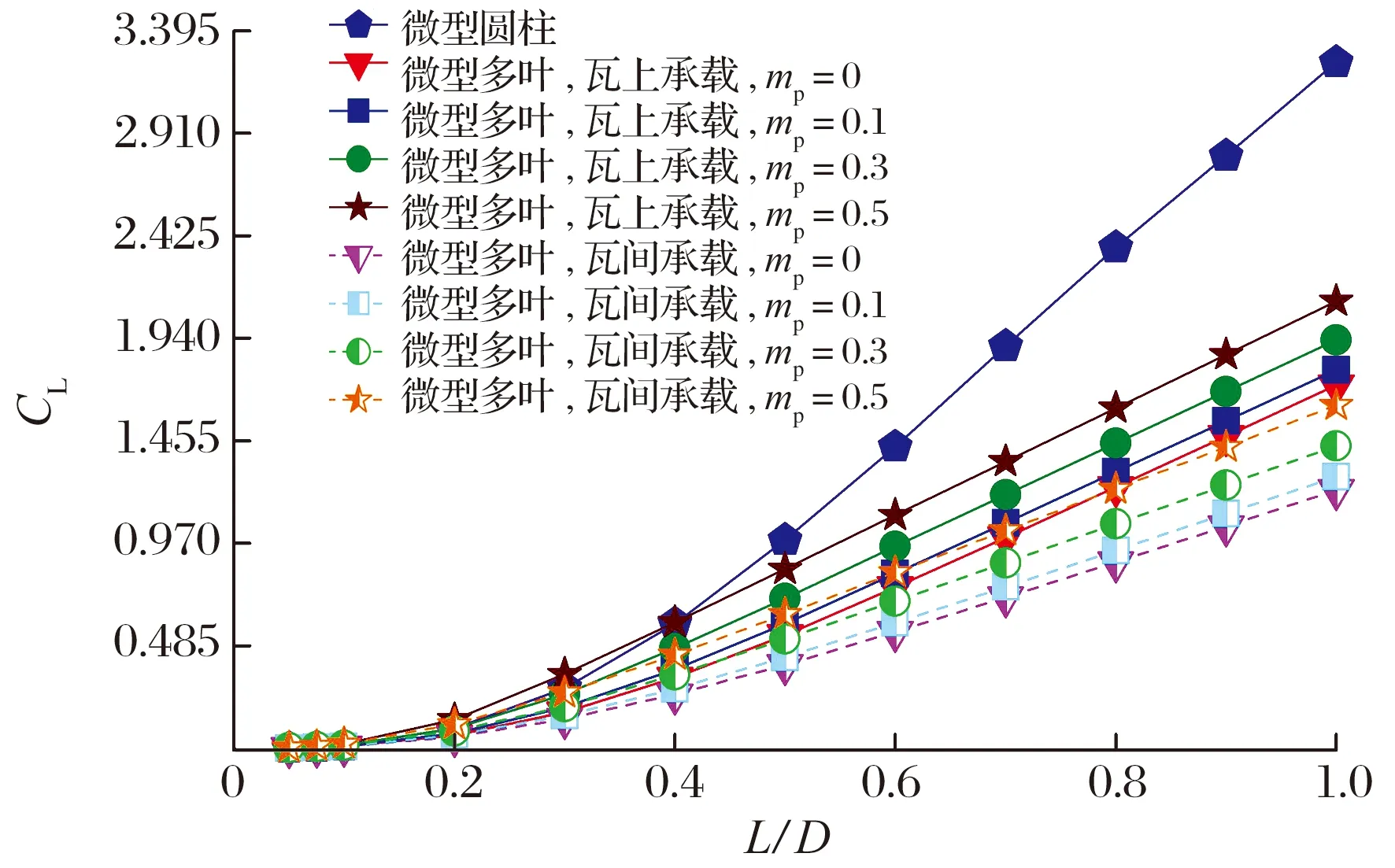
圖8 長徑比和預載荷系數對軸承承載力和摩擦因數的影響

當Λ=10,L/D=0.1時,偏心率和預載荷系數對軸承承載力和偏位角的影響如圖9所示:隨著偏心率的增加,承載力呈拋物線加速上升,這是由于偏心率越大,氣膜厚度越小,形成壓力場的壓力越高,相應預載荷系數增加也可解釋為氣膜厚度的減小,提高了微型氣體軸承的承載能力;相同偏心率條件下,瓦間承載時的承載力大于瓦上承載時,而且這種趨勢在大偏心率時更突出,這是因為偏心率較大時,轉子與瓦塊的表面間隙極小,氣體稀薄效應顯著,從瓦間溝槽吸入的氣體可有效降低氣體稀薄程度,從而提高整體微型氣體軸承的承載能力;但當ε′=0.9時,軸承內氣膜厚度很小,從瓦間軸向槽內補充的氣體不足以抵消稀薄效應對承載力的減弱作用, 此時微型圓柱氣體軸承的承載力較高;偏位角隨偏心率的增加而減小,說明承載力越大對應偏位角越小,偏心率ε′<0.4時,偏位角的變化幅度不明顯。

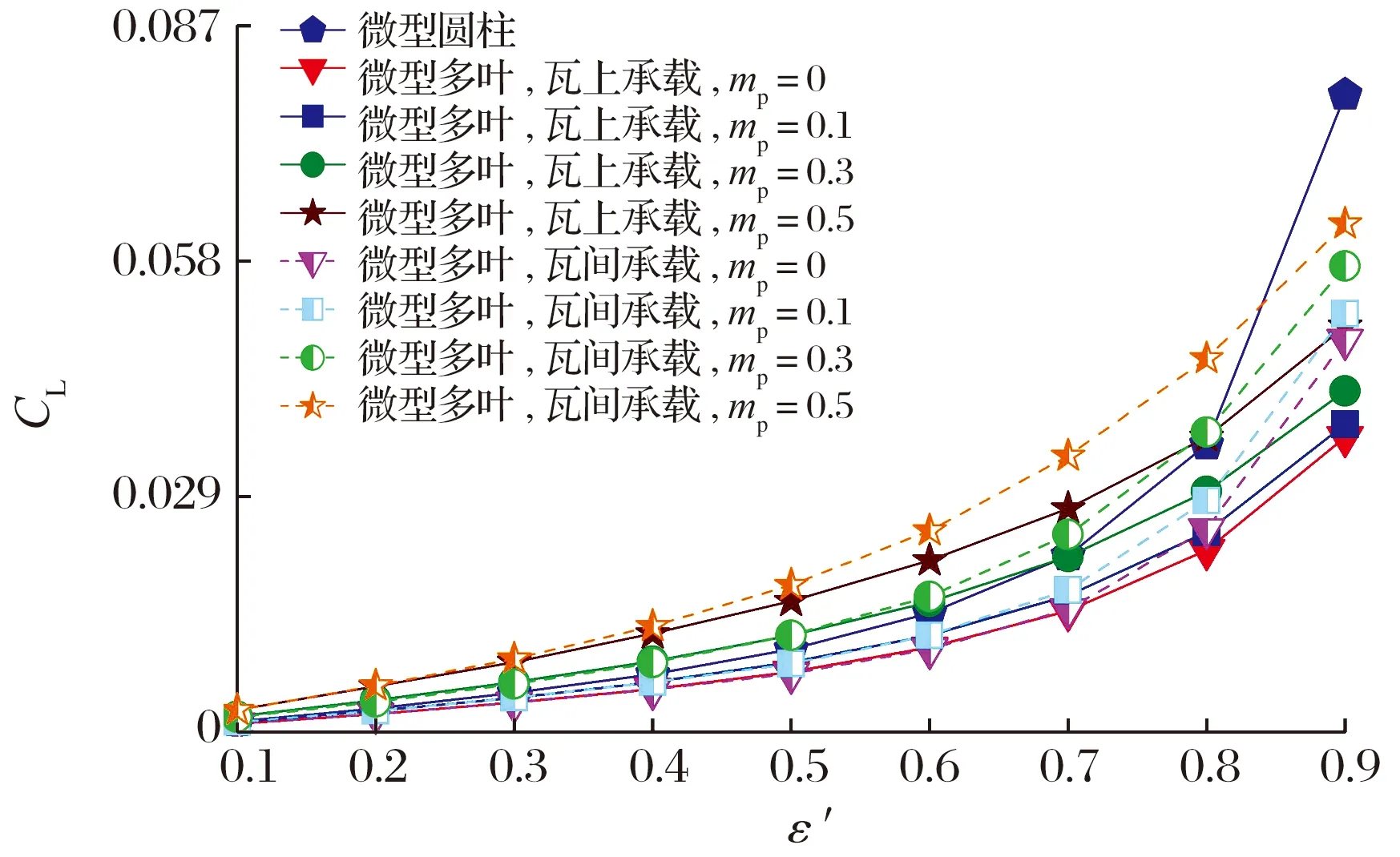
圖9 偏心率和預載荷系數對軸承承載力和偏位角的影響

當Λ=10,L/D=0.1時,偏心率和預載荷系數對軸承摩擦因數的影響如圖10所示:摩擦因數隨偏心率增加而逐漸增大,這是因為偏心率變大導致氣膜厚度減小,剪切應力提高;當ε′<0.5時,摩擦因數的增幅比較平緩,而偏心率較大時,摩擦因數快速增大;摩擦因數的增幅隨預載荷系數的增加而顯著增大;當ε′>0.5時,瓦間承載時的摩擦因數明顯大于瓦上承載時,這是因為微型多葉氣體軸承軸向溝槽泵吸的氣體增大了膜厚方向速度梯度的剪切作用,同時氣體稀薄程度的降低有效增大了氣體黏度。

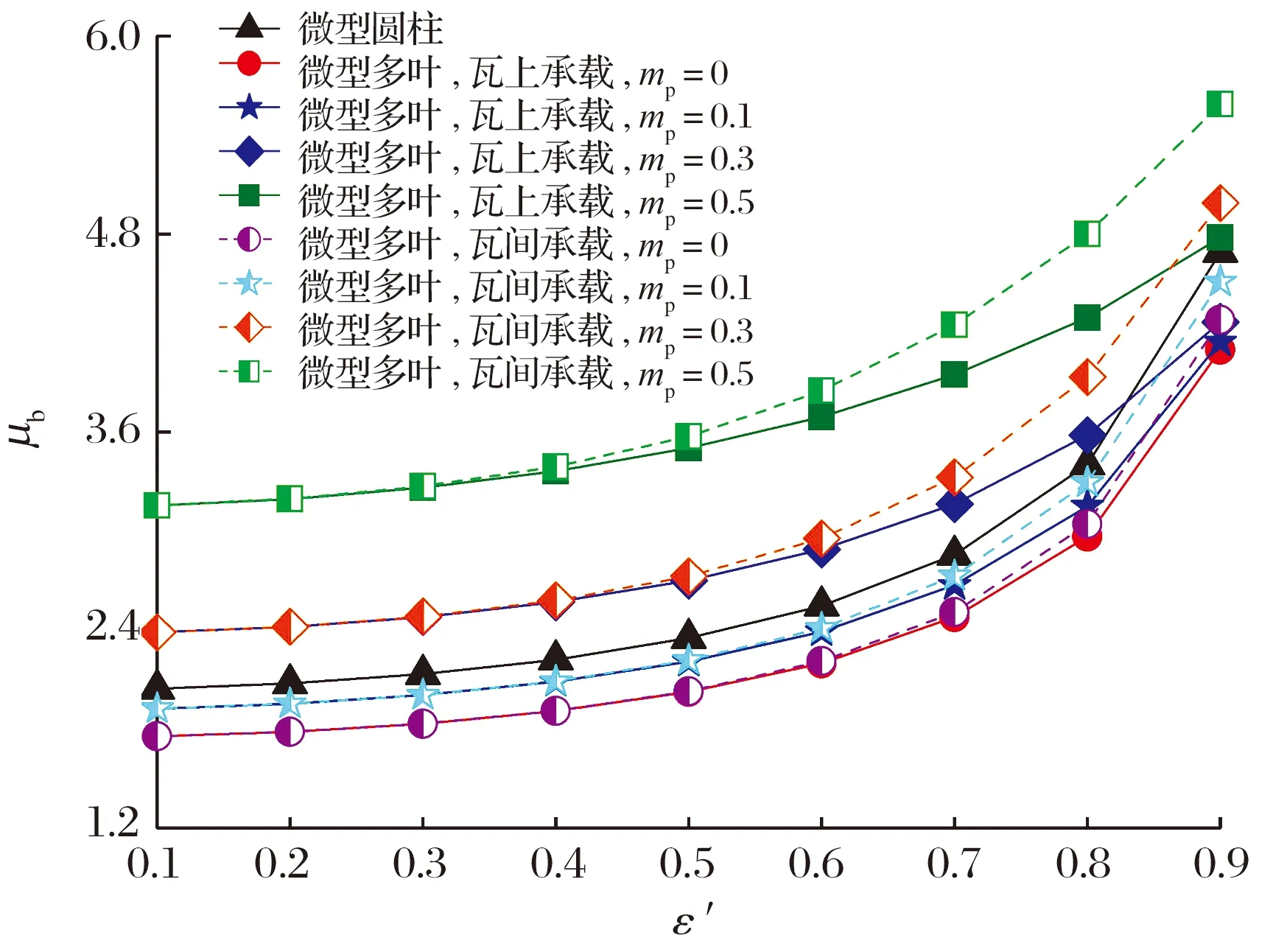
圖10 偏心率和預載荷系數對軸承摩擦因數的影響

4 結論

本文介紹了微型多葉氣體軸承稀薄氣體潤滑的靜態修正雷諾方程及有限差分數值求解過程。研究了預載荷系數、瓦塊承載方式和軸承參數對軸承靜態性能的影響規律,得到以下結論:

1)當軸頸轉速、偏心率和預載荷系數增加,瓦間溝槽吸入外部氣體大幅降低了氣體稀薄程度,氣流相互作用增強,膜厚方向速度梯度的剪切作用加劇,瓦間承載微型多葉氣體軸承的氣膜壓力最大,瓦上承載次之,微型圓柱氣體軸承最小,而且瓦間承載時的摩擦因數大于瓦上承載時。

2)隨著軸頸轉速和長徑比的增加,承載力均近似線性增加,這是因為提高軸頸轉速增強了軸承的動壓效應和稀薄氣流的密度,增加長徑比增大了各瓦塊的承載面積。

3)承載力隨偏心率的增加呈加速上升的趨勢,當偏心率接近0.9時,瓦間溝槽泵吸外部氣體提高承載力的作用要弱于氣膜厚度減小帶來稀薄效應降低承載力的作用,這時微型圓柱氣體軸承的承載力較大。