基于單天線相位的UHF RFID室內定位算法研究

陳港能,朱洪輝

(1. 漳州理工職業(yè)學院印刷傳媒與藝術學院,福建漳州,363000;2. 漳州理工職業(yè)學院機電與信息學院,福建漳州,363000)

射頻識別技術(RFID)屬于無線非接觸式系統(tǒng),對目標的識別是通過射頻信號自動完成的,以此來獲取相應的目標信息[1]。通過研究可知RFID 系統(tǒng)是由標簽、閱讀器、天線3 個部分組成。該系統(tǒng)的優(yōu)勢是非接觸、非視距。UWB、超聲波、WiFi 等[2]現(xiàn)已成為室內定位時常用的技術,相比于這些技術,UHFRFID 定位系統(tǒng)的成本較低[3]。經過與有源RFID 系統(tǒng)進行比較可以看出無源RFID 系統(tǒng)的優(yōu)勢更加顯著,由于標簽較輕使得攜帶更加方便,不需要對標簽電源進行內置處理。在對定位進行衡量時涉及多個指標,定位誤差是不可避免的[4]。對有源RFID 定位系統(tǒng)進行研究后發(fā)現(xiàn)其亟待解決的是定位誤差較高的問題。如果將傳統(tǒng)定位技術應用于室內定位之中,則要面對硬件成本高和覆蓋范圍小等困擾[5]。受移動通信技術和物聯(lián)網速度不斷加快的影響,在室內定位領域技術中,基于RFID 的室內無線定位技術因其非視距、靈敏度高、環(huán)境適應力較強等特點成為優(yōu)選[6]。因室內環(huán)境有多徑效應、噪聲干擾的影響存在,現(xiàn)有RFID 室內定位方案存在定位精度較低、過于依賴網絡等缺陷。因此,本文基于單天線相位的UHF RFID,對室內定位算法進行了研究。

1 載波相位與副載波相位

展開相位信息的提取可通過多載波信號方式進行,可對絕對信號傳播距離進行計算,展開相位信息受多途徑傳播環(huán)境影響,與絕對距離間存在較大誤差[7]。在單頻副載波調幅方式下,假設發(fā)射出頻率的3 個高頻載波信號分別為fc-fs、fc、fc+fs,其中fc-fs為初始載波信號頻率,fs為副載波信號頻率; 在多途徑傳播環(huán)境中,如果視距與非視距傳播路徑中信號傳播距離已經確定,分別記為dlos和di,則多徑傳播信道增益為:其中,Γi表示網絡輸入端的反射系數(shù)。

3 個高頻載波信號相位值φc-s、φc、φc+s可分別表示為:

其中,kc-s、kc、kc+s分別表示3 個載波對應的k值,βc-s、βc、βc+s分別表示在視距傳播路徑中3 個高頻信號累積的相位信息。通過提取3 個高頻載波信號的相位信息,可以計算副載波信號和載波信號之間的多路徑頻率和相位偏移率。

1.1 副載波相位偏移量計算

副載波相位的計算公式為φs=(φc+s-φc-s)/2,相應傳播距離為ds=(φs/(2πfs))·c,標簽位置距離為Ds=ds/2=m·(λc/2)+l1,其中初始載波信號fc的波長為λc;m為正整數(shù),半波長范圍內的l1∈[0,λc/2]。

1.2 載波相位偏移量計算

基于載波信號fc的相位值φc,信號傳播距離的計算公式為

鑒于在實際提出的載波信號相位信息中出現(xiàn)周期模糊的問題,實際信號傳播距離計算公式為其中,[·]為下取整運算。

基于φc估計出的標簽位置距離為

1.3 計算閱讀器和標簽真實間距

設d為閱讀器與標簽之間的真實間距,引入d和載波fc的波長λc的關系式:

式(1)中,n為正整數(shù),半波長范圍內的l2∈[0,λc/2]。

1.4 標簽位置距離與真實距離之間的關系

做出如下假設:n≤m,以副載波信號、載波信號相位信息為基礎可得到標簽位置距離與真實距離間的關系,具體見圖1。

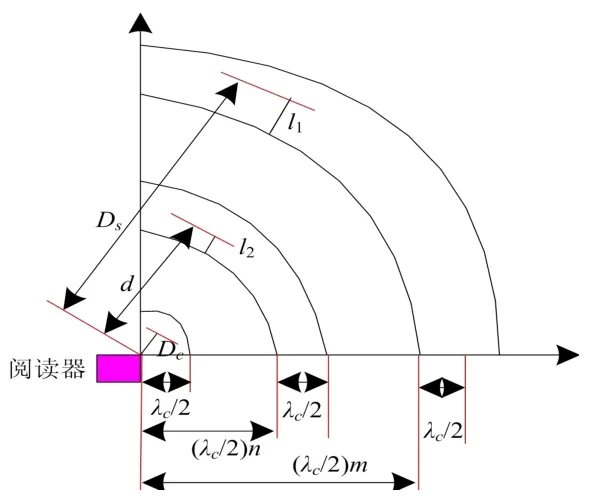
圖1 信號距離關系圖

副載波相位信息因受多途徑傳播信道影響有誤差存在,直接測距則誤差較大[8]。由于在m值和n值間存在較大測距誤差,在l1值和l2值間存在較小誤差。不使用參考標簽時,提高基于相位信息測距精度的關鍵在于減少m值和n值間差異。在多途徑傳播環(huán)境中的相鄰位置處,分析m值、n值差異,載波信號相位信息測距值Dc∈[0,λc/2]。在多途徑傳播環(huán)境中對Dc值與l2值的差異進行研究,需要比較的是l1值和Dc值在0～λc/2 范圍內準確性的情況。

假設載波頻率fc為921 MHz,副載波頻率fs為2.5 MHz; 在y軸方向上,以1.5～6.5 m 作為閱讀器和標簽距離d的變化范圍,以1 m 作為步長; 在距y軸同一距離d之上放置2 個標簽,其位置在x軸方向上,標簽1 與標簽2 的坐標分別為(2.2,d)、(2.365,d)。由此可以做出判斷,標簽1 與標簽2 在x軸上的距離確定為0.165 m,該數(shù)值與λc/2相接近,即為1/2 載波波長; 假設墻面與閱讀器距離為4.5 m,有2 條傳播路徑在閱讀器和每個標簽通信之中存在,一條是墻面反射的非視距傳播路徑,另一條是墻面反射視距傳播路徑,其中地面介質相對介電常數(shù)r為5,電導率σ為0.002。表1 為m值和n值的差異。

由表1 可知,n值和m值間無絕對大小關系,這表明對于測距誤差而言,多途徑傳播產生的影響不易估計。將標簽1、標簽2 的m值求平均,可在一定程度上將n值、m值間的部分差異減少。在定位場景中,閱讀器和標簽2 間的距離大于其和標簽1 的距離,以標簽1 作為標簽2 的m值補償,以此來保證標簽1 與標簽2 閱讀器位置方向關系。表2 為半波長范圍內l1值、l2值和Dc值的差異。

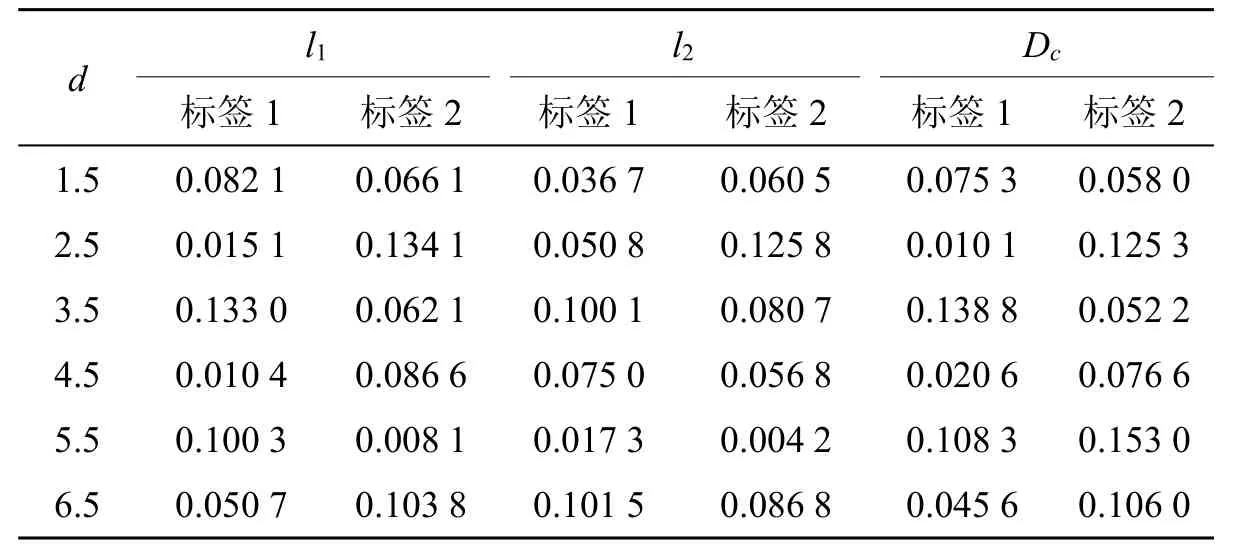
表2 半波長范圍內l1 值、l2 值和Dc 值的差異 /m

由表2 可知,標簽1、標簽2 的Dc值與l2值大小關系一致,標簽1、標簽2 的l1值與l2值間具有明顯差異,總體而言,Dc值比l1值要優(yōu)。在d=5.5 m 時,標簽1、標簽2的Dc值與l2值有差異存在,34×(λc/2)+0.008 1=33×(λc/2)+0.153 0 為標簽2 與閱讀器間真實距離,標簽1、閱讀器間真實距離為33×(λc/2)+0.100 3。若采用聯(lián)合標簽1、標簽2 的m值求平均方式,結合標簽1、標簽2 的Dc值,則閱讀器、標簽2 估計距離為33.5×(λc/2)+0.153 0; 閱讀器、標簽1 間估計距離為33.5×(λc/2)+0.108 3; 標簽1、標簽2 估計距離比實際距離0.5×(λc/2)要大,標簽2、閱讀器間距離大于標簽1 距離真實情況得到保證。結合表1、表2 實驗結果,提出基于雙標簽兩步測距定位方法。

2 基于雙標簽的測距定位方法

通常情況下,運用在倉儲空間條件下的待定位目標的體積都比較大,諸如大尺寸的紙箱和大容量編織袋,而無源標簽體積則很小,使用無源標簽體積為5.50 cm×5.50 cm×0.03 cm; 在大體積待定位目標上,附著無源標簽兩個定位[9]。如果2個標簽處于較近的位置,則多途徑傳播的環(huán)境把求平均運算與載波相位信息兩種方法結合起來使用,可以使副載波相位偏移量的測距誤差隨之減少[10]。

2.1 基于雙標簽的測距方法

以往研究中側重于信號展開相位信息,較為忽視存在周期模糊的卷疊相位信息,本文使用將信號的卷疊相位信息、展開相位信息相結合的測距算法。假設在同一平面上,待定位目標附著標簽1、標簽2,圖2為雙標簽法二維平面圖。1–d 為標簽1 閱讀器的視距距離,2–d 為標簽2 的相應距離。在多途徑傳播信道,因有相位偏移引入,視距距離1–d、2–d 是由標簽1 與標簽2 所做出的估計,與實際距離存在偏差。

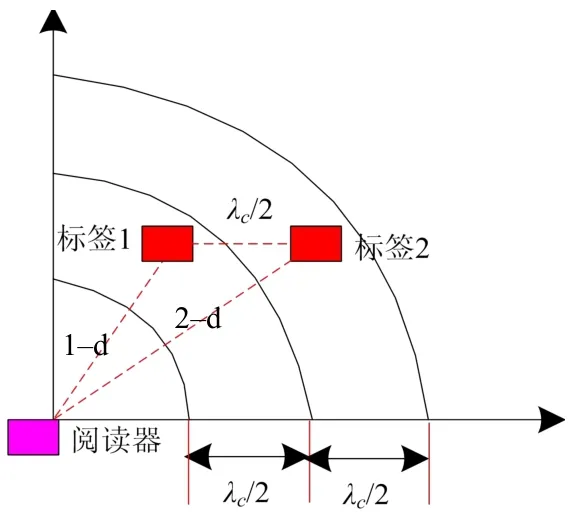
圖2 雙標簽法

結合表1,視距傳播路徑不同,標簽的距離比較接近,但是相位偏移的問題會受到多途徑傳播的影響而產生,且問題較為顯著。所以在本次研究中提出采用雙標簽兩步測距的方法,根據副載波信號相位信息得到距離計算正整數(shù)mi,其計算公式為其中,[·]為下取整,i∈{1,2}為雙標簽編號。

對雙標簽各自對應的正整數(shù)m1、m2進行計算。相比于式(1)中準確的正整數(shù)值n,m1和m2均有偏差存在,求m1和m2的平均值m,減少差異,即

利用載波相位計算距離Dc,i,設ai為標簽i閱讀器的距離估計值,則可由下式求得估計距離m:

這里采取的是同時附著雙標簽部署的方法,提取副載波信號相位信息是在待定位目標上完成的,對2 個標簽與閱讀器間的距離進行估計。

2.2 基于雙標簽的定位方法

在傳統(tǒng)幾何定位方法中,使用多個閱讀器方式,在待定位區(qū)間的不同方位處分布閱讀器,通過圓相交方式對待定位標簽坐標位置做出準確的估計[11]。雙標簽處于三維空間內可以進行拓展后成為三標簽。假設(x,y)為待定位目標坐標,標簽1 坐標為(x1,y1),標簽2 坐標為(x2,y2),Δd為標簽1 和標簽2 間的間隔,在Δd=λc/2 的條件下,為了確定標簽1、標簽2 閱讀器天線與(0,0)的距離(分別記為a1、a2),可以把兩步測距的方法應用于其中,即

標簽1、標簽2 的坐標關系滿足:

計算出標簽1 的坐標解為

再利用公式x=(x1+x2)/2,y=(y1+y2)/2,解得標簽2 的坐標解x2,y2。其中,(x,y)為待定位目標的坐標。坐標x1＜0 的情況很可能在式(5)中產生,之所以出現(xiàn)這種問題是由于所采取的是兩步測距法,以式(2)為依據確定標簽1 和標簽2 正整數(shù)是一致的。比較標簽2 與標簽1 后,前者正整數(shù)m2比后者正整數(shù)m1多1,在式(2)后,標簽2、標簽1 具有相同的正整數(shù),這樣會減小標簽2 與閱讀器距離。標簽2 與閱讀器的距離在數(shù)值上差半波長λc/2,因標簽1、標簽2 間坐標滿足式(4),會使定位結果有較大誤差出現(xiàn),而這些誤差對于某些應用場景則會產生一定的影響。比如在登記倉儲入口處的物品時,如果物品已被閱讀器左半面空間進行了登記,那么右半面屬于需登記物品,而右半面空間內包括了標簽1 和標簽2,但是受到距離誤差的影響而做出錯誤的判斷,將其劃歸為左半面,即已登記貨物,這會引發(fā)貨物登記混亂,需修正。在進行標簽位置誤判修正時,標簽1、標簽2 間距離為半波長λc/2,可確保標簽2 與閱讀器距離一直超過標簽1 與閱讀器的距離,能夠精確把標簽2 與閱讀器距離中的半波長數(shù)倍展示出來,即與標簽1 相應距離中的半波長整數(shù)倍進行比較要超出1。所以標簽2 在x1＜0 的條件下距離a2要補上載波波長值的1/2,即a2=a2+(λc/2)。

在定位多閱讀器中,不能預先做出標簽與閱讀器間遠近程度的判定,貨物登記誤差的問題往往會在倉儲入口應用場景中產生,從而導致重大損失。為了妥善解決此問題需要使用多標簽的辦法,在此方式下進行定位可通過單閱讀器天線來完成,降低硬件設施的成本,本算法的流程圖如圖3 所示。

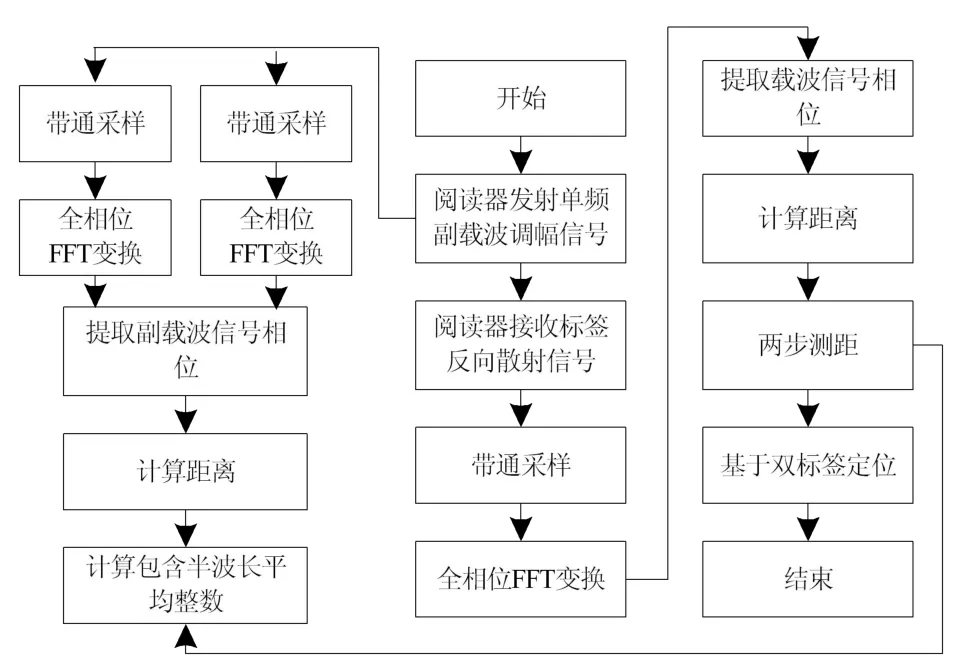
圖3 基于雙標簽的定位方法流程框圖

3 仿真結果分析

仿真實驗在Matlab 工具軟件中進行,仿真場景為一倉儲入口,尺寸為4.5 m×8.5 m; 以坐標原點(0,0)作為閱讀器天線的位置,假設待定目標的數(shù)量是105 個,有2 個標簽附著于每個待定位目標上,而且入口中心線是對稱的。在y軸方向上,閱讀器和待定位目標距離為任意長度; 閱讀器副載波頻率為2.5 MHz,載波頻率為921 MHz,信噪比為10.2 dB,仿真次數(shù)為105 次。待定位標簽i測距估計值與實際值di,j間的平均測距誤差f的計算公式為其中,M為標簽數(shù),N為仿真次數(shù)。

待定位目標i估計值(xi0,yi0)與實際值(x,y)間的定位均方根誤差e的計算公式為

平均定位誤差eave的計算公式為其中,Q為待定位目標數(shù)。

接下來做如下設想: 有2 種多途徑傳播路徑,分別為兩條和三條。其中一條來自墻壁單次反射路徑,和另一條視距傳播路徑組成兩條傳播路徑; 在前面兩條的路徑上再加一條墻壁雙次反射路徑,共同組成了3 條傳播路徑。在直接利用副載波相位估計標簽距離Ds后測距部分隨之形成,該方法稱之為單步測距; 在對估計標簽距離時所采用的是兩步測距法(載波),這是在雙標簽的基礎上形成的方法; 由公式(3)可知,載波相位計算距離Dc,i可以被副載波相位計算距離ll所替換,以此作為兩步測距(副載波),通過比較兩步測距(載波)、兩步測距(副載波)2 種方法的定位誤差后定位部分隨之形成; 如何理解兩步測距(副載波)、統(tǒng)計兩步測距(載波)方法判別率的問題,從其實質來看是對物品是否屬于未登記做出判定,這是在待定位目標估計位置的基礎上完成的,表3 為3 種測距方法的平均測距誤差。

表3 測距誤差

由表3 可知,在兩條路徑條件下,兩步測距(載波)方法平均誤差為0.210 m; 兩步測距(副載波)方法平均誤差為0.200 m; 單步測距方法平均誤差約為0.322 m; 以兩條路徑作為前提條件可以確定用這3 種方法都會有測距誤差產生,而且差異是相類似的,由此可以做出判斷,兩步測距法比單步測距法準確性更高,可以減少測距誤差。圖4 為載波和副載波2 種情況下運用兩步測距法產生的誤差概率對比。

由圖4 可知,在三條路徑、兩條路徑情況下,兩步測距(載波)方法最大誤差分別為0.92、1.00 m,估計平均定位誤差分別為0.55、0.50 m; 在三條路徑、兩條路徑情況下,兩步測距(副載波)方法最大誤差分別約為0.97、1.00 m,估計平均定位誤差分別為0.57、0.54 m; 這表明兩步測距(載波)方法對本研究提出的基于雙標簽的定位方法更加適合。而對于測距誤差,兩步測距(副載波)方法和兩步測距(載波)方法相差雖較小,但在基于雙標簽的定位中,無法確保閱讀器與2 個標簽間距離大小關系。貨物登記狀態(tài)誤判問題在倉儲空間場景中十分重要[12]。在105 次仿真實驗中,對105 個待定位目標進行統(tǒng)計。兩步測距(載波)分別在三條路徑、兩條路徑的條件下誤判率都是0,兩步測距(副載波)方法誤判率分別為17.45%、17.82%。說這表明兩步測距(載波)方法具有較高的準確性,可以降低定位誤差,對物品能夠做出準確的登記,適用于本次仿真場景[13]。圖5 為UHF RFID 陣列天線方位測試場景圖。

圖5 UHF RFID 陣列天線方位測試場景圖

4 結論

伴隨著無線定位技術的應用推廣,此項技術也由室外逐步擴展到室內,這也讓無源UHF RFID 室內定位技術得到廣泛的應用,其優(yōu)勢在于無源標簽體積較小,因此基于標簽室內定位技術引起各界關注而成為研究的重點內容。本文基于單天線相位的UHF RFID,對室內定位算法進行了研究,得出如下結論:

(1)如果待定位目標邊長距離要超過高頻載波信號波長,有2 個間距附著于待定目標上,此無源標簽是載波波長的1/2。處于單閱讀器天線的條件下定位閱讀器與標簽間存在三角幾何關系。使用2 個無源標簽可以對測距誤差進行調整,把定位誤差降下來。

(2)仿真表明,在三條路徑、兩條路徑情況下,兩步測距(載波)方法最大誤差分別為0.92、1.00 m,估計平均定位誤差分別為0.55、0.50 m; 兩步測距(副載波)方法最大誤差分別約為0.97、1.00 m,估計平均定位誤差分別為0.57、0.54 m; 但兩步測距(副載波)方法基于雙標簽定位中,無法確保閱讀器與2 個標簽間距離大小關系。

(3)在三條路徑、兩條路徑情況下,兩步測距(副載波)方法誤判率分別為17.45%、17.82%,兩步測距(載波)方法誤判率均為0。因此,兩步測距(載波)方法可將定位誤差降低,確保物品登記的準確性。