基于熵權的全局記憶LF蟻群聚類算法

熊偉超　蔣瑜

摘 要：針對LF蟻群聚類算法沒有區分數據集屬性重要度、算法效率低和聚類效果不穩定的問題，提出一種基于熵權的全局記憶LF算法（weighted global ant colony optimization，WGACO）。該算法首先通過熵權法計算各屬性熵權，修改歐氏距離計算公式，以提升聚類精度；使用權重最大的屬性值對數據對象進行初始化，增強聚類效果的穩定性；引入全局記憶矩陣減少螞蟻的無效移動，提升算法效率；加入算法的收斂條件，提升算法實用性。選取UCI數據庫中的7個真實數據集和3個人工生成的數據集進行數值實驗，并與GMACO、SMACC、ILFACC三種改進LF的算法進行比較，實驗結果表明，所提算法在精度、算法效率和穩定性上都有比較好的提升，在處理高維數據上也有較好的表現。最后，WGACO在商場會員用戶細分上表現良好，體現了其實用價值。

關鍵詞：LF蟻群聚類；信息熵；屬性權重；全局記憶

中圖分類號：TP18 文獻標志碼：A 文章編號：1001-3695（2023）10-026-3053-06

doi：10.19734/j.issn.1001-3695.2023.02.0046

Global memory LF ant colony clustering algorithm based on entropy weight

Xiong Weichao，Jiang Yu

（College of Software Engineering，Chengdu University of Information Technology，Chengdu 610200，China）

Abstract：Aiming at the problem that LF ant colony clustering algorithm does not distinguish the importance of data set attri-butes，the algorithm efficiency is low and the clustering effect is unstable，this paper proposed a weighted global memory ant colony optimization （WGACO） based on entropy weight.Firstly，it calculated the entropy weight of each attribute by entropy weight method，and modified the Euclidean distance calculation formula to improve the clustering accuracy.It initialized the data object with the value of the largest weight attribute to enhance the stability of the clustering effect，and introduced the glo-bal memory matrix to reduce the invalid movement of ants and improve the efficiency of the algorithm.It added the convergence conditions of the algorithm to improve the practicability of the algorithm.Selecting seven real data sets and three artificially generated data sets in UCI database for numerical experiments，and compared WGACO with GMACO，SMACC and ILFACC three improved LF algorithms.The experimental results show that WGACO has a relatively good improvement in accuracy，algorithm efficiency and stability，and also has a good performance in processing high-dimensional data.Finally，WGACO has performed well in the segmentation of mall member users，reflecting its practical value.

Key words：LF ant colony clustering;information entropy;attribute weight;global memory

0 引言

聚類技術能夠根據數據本身發現其內在規律，經常作為數據挖掘中重要的預處理步驟。為了應對各種各樣的數據，越來越多的聚類算法被提出。蟻群聚類算法通過模擬自然界中工蟻堆積螞蟻尸體的行為實現聚類，相比于傳統聚類LF算法無須指定聚類個數、算法魯棒性更強、更易實現并發分布式計算，并具有抗噪聲數據的特點。但是，蟻群聚類算法也存在算法效率較低和算法參數較多的缺點。Deneubourg等人［1］通過研究自然界螞蟻堆積尸體的行為，提出了解釋蟻群聚類現象的BM（basic model）模型。Lumer等人［2］在BM模型的基礎上提出了LF算法。隨后，眾多學者的改進主要圍繞著提升算法效率和降低算法參數影響。

在提升算法效率上，劉艷等人［3］加入了信息素來控制螞蟻移動的隨機性，并通過減少數據集屬性維度有效地提高了算法聚類效率。牛永潔［4］利用全局記憶矩陣代替之前螞蟻的局部記憶，螞蟻在全局信息下向最優位置移動而不是直接跳轉到該位置，減少了螞蟻的無效移動并避免陷入局部最優。高陽［5］通過Spark平臺實現了算法的并行處理，增加了算法對大量數據的處理能力。王昕宇等人［6］在文獻［4］的基礎上加入了首次找準原則和相異原則，加快了螞蟻找到數據的速度，提升了算法效率。沈興鑫等人［7］設計了相似度矩陣，將螞蟻隨機移動方式優化為按照相似度系數規則實施目的性的關聯，加速了數據聚集。Chen等人［8］賦予螞蟻更快的搬運速度，減少算法迭代時間。

在降低參數影響上，朱峰等人［9］通過螞蟻放下數據對象失敗的次數與迭代次數的比值設計了聚類精細程度參數alpha的數值變化公式，實現了alpha參數的自適應。劉陽陽等人［10］根據先粗分再細分的思想，階段性地遞減螞蟻可視范圍R，實現了R參數的自適應，并且設計了算法結束條件，使算法能夠自主完成收斂，提高了算法的實用性。甘泉等人［11］利用區域數據的信息熵變化代替了螞蟻“拾起”“放下”的判斷條件，減少了算法參數個數。同時，不少學者對蟻群聚類算法的其他方面也進行了改進。徐曉華等人［12］在BM模型基礎上提出AM（ant movement）模型，把數據對象本身當做螞蟻，用睡眠態、激活態代替數據的撿起和放下，有效避免螞蟻的無效移動，提高了聚類的速度和質量。Wei［13］加入數據組合機制，采用抽象的蟻群聚類算法對基準問題進行了聚類，能夠有效地用于多變量聚類。此外，蟻群聚類算法還被應用在了復合物挖掘［14，15］、用戶細分［16］等領域。通過對上述的算法改進和算法本身分析發現，LF的算法效率還可以進一步提升，獨立重復運行時，算法效率和性能波動較大的問題沒有被解決。

因此，本文提出一種基于熵權的全局LF蟻群聚類算法WGACO。該算法首先使用熵權法，通過信息熵計算數據集各屬性權重，并修改歐氏距離的計算公式，使用權重最大的兩個屬性值對數據對象進行坐標初始化；同時，引入一個全局記憶矩陣和算法收斂條件。與其他改進的算法相比，本文算法聚類精度更高、聚類速度更快、算法穩定性更強。

1 LF蟻群聚類算法

LF算法將待處理的數據對象和螞蟻都隨機投影到一個指定大小的二維網格中，并限制一個網格中只能有一個數據對象。螞蟻在網格中碰到一個數據對象Oi后，用式（1）計算Oi在當前區域中的局部密度f（Oi）。

其中：d2表示數據Oi領域的大小；d（i，j）表示Oi與其領域中其他數據對象之間的歐氏距離；α為聚類的精細度，α過大，不同類數據對象之間的區分不明顯，聚類的效果變差，α過小，同類數據對象間差異被放大，聚類后簇的個數會多于實際的簇數，算法運行時間也會變長。

用式（2）將f（Oi）轉換為螞蟻撿起Oi的概率。

其中：Kp是螞蟻撿起Oi的難度系數。如果Ppick大于一個隨機數，螞蟻撿起Oi，在自己的記憶中找到與Oi最匹配的位置后，螞蟻攜帶Oi向該位置隨機移動。攜帶Oi的螞蟻移動到新位置后，如果該位置沒有被占用，首先用式（1）計算f（Oi），之后用式（3）將f（Oi）轉換為螞蟻在該位置放下Oi的概率Pdrop。

其中：Kd是螞蟻放下Oi的難度系數。如果Pdrop大于一個隨機數，螞蟻在該位置放下Oi，并在自己的記憶中記錄該位置，之后重復之前的動作，蟻群經過若干次迭代后就能夠實現對所有數據對象的聚類。

2 基于熵權的全局LF蟻群聚類算法

2.1 熵權法

在數據集中每個屬性對聚類的貢獻程度不同，區分不同屬性的重要度能提高聚類的準確度、加速聚類。在統計學中，某個數據屬性信息熵越小，數值離散程度越大，則認為該數據屬性包含的信息越多，對應的權重越大。熵權法是一種通過各數據屬性本身的信息熵計算對應權重的方法，并會對得到的結果進行一定的修正，使得到的屬性權重較為客觀。對第j個數據屬性，用式（4）計算其信息熵。

2.2 穩定的數據初始化策略

在LF算法中，數據對象的初始位置是隨機的。由于數據集中的數據對象S可以與多個類的數據對象聚集，算法獨立重復運行時，每次隨機得到的初始化結果不同，S周圍數據對象的分布情況都不一樣，導致S有時候先碰到同類對象被正確聚集，有時候先碰到異類對象被錯誤聚集，S對象數量越多，算法聚類效果波動越大，下文給出了數據對象S的定義。每次隨機初始化后，同類對象之間的距離也不同，距離短算法迭代快，距離長算法迭代慢，算法運行時間也有較大波動。圖1是LF在UCI數據集iris、wine、seed上獨立重復運行10次的運行時間和ARI［17］數值，從圖中可以觀察到，LF算法的聚類效率和聚類精度波動較大，驗證了上述分析，隨機初始化的方式的確會影響LF的穩定性。

為了增強算法效率的穩定性，需要一個穩定的初始化結果，同一個對象初始化位置固定，為了解決算法精度不穩定的問題，使S能夠被正確聚集，需要使S周圍有更多的同類對象，增加其在被搬運過程中先碰到同類對象的概率。考慮數據對象本身的屬性值是不變的，并且同類對象在同一屬性上的值相近。因此，使用數據對象自身屬性值對其進行坐標初始化可以得到穩定的初始化結果，并且同類對象在網格上的位置接近，S周圍也會有更多的同類對象。由于同類對象在權重最大的屬性上值最接近，異類對象在該屬性上值最不同。所以，在數據集所有的屬性中，使用權重最大屬性值對數據對象進行初始化可以使同類對象在網格上的位置最接近，并且不同類別的對象所處的區域有明顯的間隔，更容易執行聚類操作。具體定義如下：

定義1 數據對象S。與同類對象和異類對象在歐氏距離度量上區分不明顯，容易被錯誤劃分的對象。

定義2 權重最大屬性。數據集中，在數據對象分類中貢獻度最大的屬性。

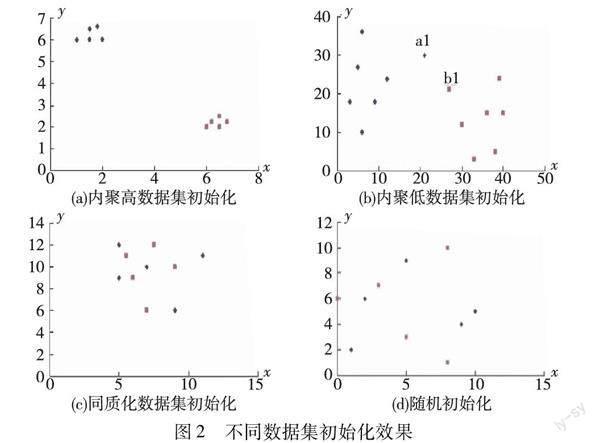
聚類數據集根據自身特點可以劃分為數據內聚度較高數據集、數據內聚度較低數據集和高維數據集。圖2是不同類型數據集的初始化效果，圖（a）～（c）是使用權重最大屬性值初始化的理想效果，圖（d）是隨機初始化效果。接下來結合圖2分析使用權重最大屬性值初始化在不同類型數據集上的普適性：

a）數據內聚度較高的數據集。該類數據集是比較理想的聚類數據集，圖（a）是這類數據集使用權重最大屬性值初始化的效果。因為數據內聚度高，所以，這類數據集一般沒有S對象，初始化后不會提升聚類精度及其穩定性。但是從圖中可以看出，同類對象初始位置非常接近，甚至能夠達到初步聚類的效果，算法效率會得到顯著的提升。

b）數據內聚度較低的數據集。大多數真實數據集屬于該類。圖（b）是這類數據集使用權重最大屬性值初始化的結果，由于數據內聚度低，類之間的邊界不明顯，有可能出現S對象。在LF算法中，為了避免局部最優，螞蟻搬運對象的方向有隨機因素的影響。如果圖中的a1、b1為數據對象S，從a1、b1周圍對象的分布情況來看，其在被搬運的過程中先碰到同類對象的概率與先碰到異類對象的概率幾乎相同。如果圖中的其他對象為數據對象S，其先碰到同類對象的概率遠大于先碰到異類對象的概率。因此，使用權重最大屬性值對該類數據集初始化不僅能夠提升算法效率，還能夠提升算法聚類精度。

c）維度高，不同類別對象在權重最大屬性上差異較大的數據集。其初始化效果類似圖（b）。高維屬性往往會使各對象在歐氏距離上難以區分，所有對象之間都能夠相互聚集，算法的初始化策略不會對算法效率及其穩定性產生影響。在這類數據集中，S對象的個數較多，使用權重最大屬性值初始化對聚類精度的提升比較明顯。

d）維度高，不同類別對象在權重最大屬性上差異較小的數據集。圖（c）是這類數據集初始化的效果，所有對象混雜在一起，不能實現聚類操作，初始化策略的改變無法影響其聚類效率和精度。

式（8）為按照屬性值的具體初始化公式。

其中：X為數據對象在網格上的坐標；N為網格長度；i為數據對象權重最大的屬性值；max為當前數據集中該屬性的最大值；min為當前數據集中該屬性的最小值。

2.3 全局記憶矩陣

LF算法中各螞蟻獨立執行聚類動作，螞蟻之間沒有信息交流。當一只螞蟻將數據對象搬運到目的數據對象附近時，該數據對象可能已經被其他螞蟻搬走，導致螞蟻無效移動。為了實現螞蟻之間的信息共享，引入一個三列的全局記憶矩陣，分別記錄數據對象索引、數據對象在當前位置的Pdrop以及數據對象失效標志，數據對象坐標信息通過索引從對象位置矩陣中獲取。加入全局記憶矩陣后，螞蟻拾起、移動、放下的處理步驟發生變化，具體如下：

a）螞蟻成功拾起數據對象后，如果全局記憶中存在該對象，將該對象設為失效點。

b）螞蟻在全局記憶中找到與當前數據對象最相似的數據對象后，向目標對象隨機移動。

c）螞蟻成功放下數據對象后，在全局記憶中用當前數據對象信息替換失效對象信息，如果沒有失效對象，將當前數據對象的Pdrop與全局記憶中最小的Pdrop進行比較，如果當前數據對象的Pdrop大于該Pdrop，用當前數據對象信息替換對應數據對象信息，否則全局記憶保持不變。

全局記憶矩陣的加入能夠實現蟻群中的信息共享，每只螞蟻都能作出當前最合適的選擇。移動的隨機性是LF算法不易陷入局部最優的關鍵，而移動的有向性能夠加速聚類，全局記憶中螞蟻向目標對象隨機移動兼顧了移動的隨機性和有向性，避免陷入局部最優的同時提升算法效率。矩陣中的失效標志列能夠快速找到替換項，減少更新矩陣時的時間。

2.4 算法自主收斂

LF中算法迭代次數是固定的，次數過低聚類效果不理想，次數過高會影響算法效率。從式（1）（2）可以發現，越是到聚類后期，數據對象周圍同類數據的數量越多，該對象與其領域對象之間的歐氏距離d（i，j）變得越小，區域密度f（Oi）變得越大，該對象被拾起的概率Ppick變得越小，該對象很難被螞蟻拾起，對應螞蟻仍保持為空載狀態。類似的對象越多，網格上處于空載狀態的螞蟻就越多。因此通過算法每次迭代結束后空載螞蟻的數量可以判斷算法的聚類進度，當算法中空載螞蟻的數量連續多次超出預設范圍后，可以認為聚類基本完成。具體的收斂條件為：當算法在連續20次迭代中空載螞蟻的數量超過總數量的90%時，算法結束。真實的數據集中難免會存在異常對象，這類對象不能與其他對象發生聚集行為，導致拾起這些對象的螞蟻一直處于負載狀態，影響算法收斂。為了避免這些數據的影響，為每只螞蟻增加一個計數器，記錄螞蟻連續放下數據對象失敗的次數，當計數器數值達到指定的次數后將當前負載的數據對象強行放下，轉而去處理其他數據對象。組合以上的改進，WGACO偽代碼如下。

算法1 WGACO算法

輸入：數據集D。

輸出：聚類結果C。

a）初始化參數如網格大小GridNum，螞蟻數量AntNum，數據數量N，聚類精細度α，鄰域半徑R，拾起難度K1，放下難度K2，全局記憶容量MemorySize。

b）計算數據集各屬性權重。

c）將得到的權重按照式（7）加入到歐氏距離的計算當中。

d）通過式（8）完成數據對象在網格上的初始化。

e）隨機選擇螞蟻，若螞蟻為空載執行步驟f），為負載執行步驟g）。

f）螞蟻隨機跳轉到一個數據對象上，通過式（1）（2）判斷能否撿起該對象。

g）螞蟻通過式（1）（3）判斷能否在當前位置放下負載的數據對象，若不能，則根據全局記憶矩陣繼續移動。

h）判斷算法是否收斂，收斂執行步驟i），否則繼續執行步驟e）。

i）輸出聚類結果。

3 算法復雜度分析

LF作為迭代的算法，其時間復雜度為O（MNK），M為迭代次數，N為螞蟻個數，K為每次迭代中每只螞蟻的計算量。由于N為事先指定的常數，所以LF算法的時間復雜度屬于O（n2）。使用新的歐氏距離，改變數據初始化策略只是使用了不同的計算公式，在時間復雜度上沒有變化。因此，WGACO的整體時間復雜度為O（MNK+T），依舊屬于O（n2），T為計算屬性權重的時間開銷。使用權重最大屬性值對數據對象進行初始化后，螞蟻搬運數據對象的距離變短，使用全局記憶矩陣后，減少了無效迭代的次數，WGACO中的M值會明顯小于LF中的M值。因此，雖然WGACO的時間復雜度與LF相同，運行效率卻會明顯提升。LF的空間復雜度為O（1），每只螞蟻都擁有常數個記憶空間。WGACO引入了全局記憶矩陣，并為每只螞蟻增加了一個計數器，依然只使用了常數個存儲空間，空間復雜度依然為O（1）。

4 仿真實驗及分析

4.1 實驗環境與實驗數據集

對比實驗在Anaconda4 jupyterlab中完成。實驗所用操作系統為Windows 10，處理器為Intel Core i5-8250U@1.60 GHz四核，內存為8 GB。表1為7個UCI數據集的說明，表2為三個由sklearn內置的make_blobs函數生成的數據集，其中cluster_std參數表示生成的數據集中同一類數據的方差大小。設置與GMACO［6］、SMACC［7］和ILFACC［8］三種改進LF的算法對比。

4.2 實驗參數

參數設置為：Kpick=0.1，Kdrop=0.15，鄰域r=2，二維網格的大小是100×100，螞蟻個數為30，全局記憶的長度為50［4］，螞蟻計數器的閾值為20。

從式（1）發現，適合每個數據集的α值不相同。因此，在實驗前需要先多次運行算法找到適合不同數據集的α值。合適的α值應該滿足以下要求：在該α值下算法能夠完成收斂；同時，為了充分驗證改進后算法的有效性，每個數據集取三個不同的α值進行對比實驗，三個α值依次增大。表3是各個數據集在實驗中的α值，第一列為在多次調試中找到的能使該數據集完成收斂的最小α值。從式（7）發現，修改后的歐氏距離計算公式縮小了屬性之間的差值，導致α的取值范圍發生變化。為了維持對比實驗的公平，其余三種對比算法也使用式（7）計算歐氏距離，將各屬性權重全部設為1/n，n為數據的屬性個數。

聚類結果的評價指標使用調整蘭德系數ARI（adjustable Rand index）［17］和F指標（F1-measure）［18］，ARI為［-1，1］，F1為［0，1］，值越大代表聚類效果越好。同時，記錄四種算法的運行時間來評估算法效率，運行時間包含數據預處理、屬性權重計算、數據集初始化、算法迭代。實驗結果中的數值都為每個算法獨立重復運行20次后的均值。

4.3 實驗結果與分析

圖3為所有數據集使用權重最大屬性值初始化的效果。初始化效果符合圖2中的預期，可以看出，data1、iris、seed屬于內聚度較高的數據集，data2、wine、Wdbc、wave屬于內聚度較低數據集，move、cover屬于在個別屬性值上有明顯區別的高維數據集，data3屬于不能聚類的數據集。圖3的實驗結果證實了使用權重最大屬性值初始化策略的普適性。

表4為四種算法的對比實驗結果。在算法效率上，WGACO在低維數據集iris、wine、seed、Wdbc、wave上表現最好，比GMACO平均快3.43倍，比SMACC平均快2.21倍，比ILFACC快1.76倍，一方面是因為WGACO在初始化后，數據集中同類對象就能基本處于網格上的同一區域，極大地縮短了算法迭代時間。初始化效果越好，WGACO的聚類效率提升效果越明顯，WGACO在初始化效果好的iris、seed、Wdbc上比其余三種算法平均快3.4倍，而在初始化效果一般的wine和wave上平均只快了1倍。因此，在數據量較小的wine數據集中，SMACC和ILFACC算法的聚類效率與WGACO相近，甚至有時能夠更快。另一方面是因為WGACO中引入了全局記憶矩陣，全局記憶相比于ILFACC中的局部記憶更具時效性，屬性熵權的加入使全局記憶信息更準確，避免了算法因過時、錯誤信息而出現的無效迭代，能夠有效地提升聚類效率。在高維數據集move、cover中，WGACO相比于其余三種算法沒有明顯優勢，這是因為較高的維度使不同簇之間的對象在距離度量上出現同質現象，所有對象互相都能產生聚集行為，數據集被聚集的速度受算法的影響變小，表4中可以發現，在最高維度的cover數據集上四種算法的聚類效率幾乎沒有差別。表4中黑體數據為同組中的最優值。

在聚類精度上，WGACO和ILFACC在五個低維數據集上的聚類精度整體高于GMACO和SMACC，因為這兩種算法都在計算歐氏距離中加入了屬性權重的調節。其中，在iris、seed、Wdbc數據集上WGACO和ILFACC的F值和ARI幾乎持平，在wine和wave數據集上，WGACO的F值和ARI高于ILFACC，平均高出9%，這是因為這兩種數據集數據內聚程度較低，數據對象S的個數較多。而在高維數據集move和cover中，WGACO的聚類精度明顯高于其他三種算法，F值和ARI平均比GMACO高18%和25%，比SMACC高17%和24%，比ILFACC高15%和23%，因為隨著數據維度的增加，在距離度量計算中無效屬性對有效屬性的干擾越來越大，單純地加入屬性權重的影響變小，ILFACC在兩個高維數據集上的聚類精度相比于GMACO和SMACC并沒有明顯提升，對象是否被正確聚類更多地取決于其周圍對象的分布情況。WGACO單獨使用權重最大的兩個屬性對數據集進行初始化，能夠避免其他屬性的干擾，相比于ILFACC算法，能夠更有效地發揮屬性權重的作用。同時，全局記憶矩陣能夠使螞蟻向當前全局最優位置隨機移動，避免了陷入了局部最優，而SMACC通過尋找聚類對象領域中的相似對象來決定該對象被搬運的方向，缺乏全局信息的指導，雖然其聚類速度快，但容易陷入局部最優，聚類精度不高。

在表4中觀察到，隨著α值的增大，四種算法都出現了聚類精度下降、運行時間減小的趨勢，從α的最小值到最大值，GMACO的F值和ARI分別下降14%和22%，SMACC分別下降11%和12%，ILFACC分別下降15%和12%，WGACO分別下降4%和6%。α為聚類的精細度系數，α變大代表所有對象在螞蟻眼中開始變得相似，此時，低維數據集中不同類別的對象開始出現不可區分的現象，其被正確聚類的概率也開始受到周圍對象分布情況的影響，與上述高維數據集的情況類似。因此，使用權重最大屬性初始化策略后，WGACO對α有一定的容錯能力，聚類精度的下降程度要比其余三種算法小。

上述分析可以得出結論，WGACO在數據內聚程度較高的低維數據集上主要為提升聚類速度，在數據內聚程度較低的低維數據集和高維數據集上主要為提升聚類精度，符合2.2節中的分析。

圖4為GMACO、SMACC、ILFACC、WGACO在各數據集上獨立運行20次后運行時間和ARI標準差的折線圖表示。從折線圖上可以直觀地觀察到，WGACO在低維數據集上運行時間的穩定性比其余三種算法強，在高維數據集上聚類精度的穩定性比其余三種算法強，符合2.2節中的分析。

4.4 算法統計測試

為了更直觀地對比不同算法之間的性能，對GMACO、SMACC、ILFACC、WGACO的運行時間和ARI使用Friedman和Nemenyi后續檢驗，α設置為0.05。Friedman檢驗是利用秩實現對多個總體分布是否存在顯著差異的非參數檢驗方法。圖5為各算法用Friedman檢驗圖表示的檢測結果，圖中橫軸為算法排序值，縱軸為算法，橫線的中點為算法平均序值，若兩條橫線有交叉，說明對應的算法之間沒有明顯性能差異。從測試結果可以直觀地發現，WGACO的聚類效果和算法效率都明顯優于GMACO，比SMACC、ILFACC表現更好。

4.5 算法應用

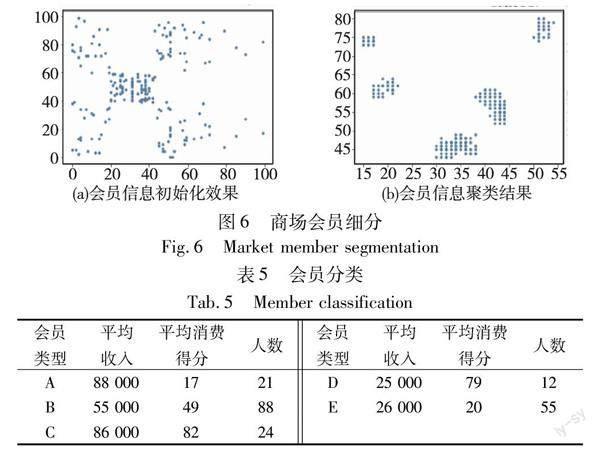
為了驗證WGACO的實用性，將其用于商場用戶細分，用于給營銷團隊的決策提供依據。mall customer segmentation data數據集是Kaggle中的商場會員信息，數據集中有200個會員信息，會員信息分別為顧客ID、性別、年齡、年收入和消費得分。由于真實的數據沒有標簽，所以用輪廓系數作為用戶細分結果的評價指標，輪廓系數為［-1，1］，值越大代表聚類效果越好。輪廓系數通過同一簇內數據的內聚程度和不同簇內數據的離散程度對聚類結果進行評價。

圖6分別是WGACO對該數據集的初始化效果和聚類結果，聚類結果的輪廓系數為0.62。表5中根據每一類會員的均值收入和消費水平將會員分為了五類，如表5所示。其中：A類會員為高收入低消費客戶；B類會員為平均收入和平均消費的客戶；C類會員為高收入高消費客戶；D類會員為低收入高消費客戶；E類會員為低收入低消費客戶。不同類型的會員之間的平均收入和平均消費得分有明顯的區別，聚類結果的輪廓系數較高，都體現了WGACO聚類結果的合理性，證明了WGACO的應用價值。

5 結束語

本文從LF算法運行時間過長、聚類效果不穩定的問題出發，提出了一種基于熵權的全局LF蟻群聚類算法（WGACO）。WGACO通過信息熵計算數據集各屬性權重，并將其加入到歐氏距離的計算當中，隨后使用兩個權重最大的屬性值作為數據對象的初始坐標，同時加入了全局記憶矩陣和算法結束條件。通過在七個UCI數據集和三個人工生成的數據集上的實驗，驗證了WGACO在聚類精度、算法效率、算法穩定性上都有較好的提升，面對高維數據也有較好的表現。通過在Kaggle用戶數據集上的應用，證明了WGACO的應用價值。

但本文算法依賴屬性權重，在實驗中發現，單一的權重計算方式在面對某些數據集時得出的效果不理想，不過改進后算法的效率有較大的提升，在屬性權重確定上多一些時間開銷是值得的。因此，后續工作中可以結合多種權重計算方法來保證權重的正確。同時，蟻群算法由于算法參數過多導致實用性較低，減少算法參數也是下一步的研究內容。

參考文獻：

［1］Deneubourg J L，Goss S，Franks N，et al.The dynamics of collective sorting robot-like ants and ant-like robots［C］//Proc of the 1st International Conference on Simulation of Adaptive Behavior.1991：356-365.

［2］Lumer E D，Faieta B.Diversity and adaptation in populations of clustering ants［C］//Proc of International Conference on Simulation of Adaptive Behavior.1994：501-508.

［3］劉艷，周斌.增量文本軟聚類速度改善算法設計及仿真［J］.計算機仿真，2022，39（8）：524-528.（Liu Yan，Zhou Bin.Design and simulation of incremental text soft clustering speed improvement algorithm［J］.Computer Simulation，2022，39（8）：524-528.）

［4］牛永潔.具有全局指導的啟發式蟻群聚類新算法［J］.計算機技術與發展，2013，23（9）：74-77.（Niu Yongjie.A new heuristic ant colony clustering algorithm with global guidance［J］.Computer Technology and Development，2013，23（9）：74-77.）

［5］高陽.一種改進的不平衡數據集過采樣方法及其并行算法研究［D］.煙臺：煙臺大學，2021.（Gao Yang.Research on an improved oversampling method for unbalanced datasets and its parallel algorithm［D］.Yantai：Yantai University，2021.）

［6］王昕宇，羅可.具有全局記憶的LF蟻群聚類算法［J］.計算機工程與應用，2019，55（20）：52-57，113.（Wang Xinyu，Luo Ke.Ant colony clustering algorithm with global memory［J］.Computer Engineering and Application，2019，55（20）：52-57，113.）

［7］沈興鑫，楊余旺，肖高權，等.基于相似度的蟻群聚類算法［J］.計算機與數字工程，2021，49（6）：1052-1057.（Shen Xingxin，Yang Yuwang，Xiao Gaoquan，et al.Ant colony clustering algorithm based on similarity［J］.Computer and Digital Engineering，2021，49（6）：1052-1057.）

［8］Chen Lianyong，Song Jinyu.Abnormal data detection method based on ant colony clustering［C］//Proc of the 6th International Conference on Electronic Information Technology and Computer Engineering.2022：66-72.

［9］朱峰，陳莉.一種改進的蟻群聚類算法［J］.計算機工程與應用，2010，46（6）：133-135.（Zhu Feng，Chen Li.An improved ant colony clustering algorithm［J］.Computer Engineering and Application，2010，46（6）：133-135.）

［10］劉陽陽，呂偉明，霍萌萌，等.基于LF算法改進的動態蟻群聚類算法［EB/OL］.（2012-04-06）［2023-04-06］.http：//www.paper.edu.cn/releasepaper/content/201204-60.（Liu Yangyang，Lyu Weiming，Huo Mengmeng，et al.Dynamic ant colony clusteralgorithm based on improved LF algorithm［EB/OL］.（2012-04-06）［2023-04-06］.http：//www.paper.edu.cn/releasepaper/content/201204-60.）

［11］甘泉，王慧.一種改進的蟻群聚類分析算法［J］.系統仿真技術，2015，11（3）：219-223，206.（Gan Quan，Wang Hui.An improved ant colony clustering analysis algorithm［J］.System Simulation Technology，2015，11（3）：219-223，206.）

［12］徐曉華，陳崚.一種自適應的螞蟻聚類算法［J］.軟件學報，2006，17（9）：1884-1889.（Xu Xiaohua，Chen Ling.An adaptive ant clustering algorithm［J］.Journal of Software，2006，17（9）：1884-1889.）

［13］Wei Gao.Improved ant colony clustering algorithm and its performance study［M］//Computational Intelligence and Neuroscience.2016：19.

［14］胡健，朱海灣，毛伊敏.基于蟻群聚類的動態加權PPI網絡復合物挖掘［J］.計算機應用研究，2020，37（2）：390-397，420.（Hu Jian，Zhu Haiwan，Mao Yimin.Dynamic weighted PPI network complex mining based on ant colony clustering［J］.Application Research of Computers，2020，37（2）：390-397，420.）

［15］胡嘉偉，吳云志，樂毅，等.基于改進LF算法的PPI網絡聚類方法［J］.湖南工程學院學報：自然科學版，2016，26（3）：56-59.（Hu Jiawei，Wu Yunzhi，Le Yi， et al. PPI network clustering method based on improved LF algorithm［J］.Journal of Hunan University of Engineering：Natural Science Edition，2016，26（3）：56-59.）

［16］Chniter M，Abid A，Kallel I，et al.Computational complexity analysis of ant colony clustering algorithms：application to students grouping problem［C］//Proc of IEEE International Conference on Systems，Man，and Cybernetics.Piscataway，NJ：IEEE Press，2022：736-741.

［17］Vinh N X，Epps J，Bailey J.Information theoretic measures for cluste-rings comparison：variants，properties，normalization and correction for chance［J］.The Journal of Machine Learning Research，2010，11：2837-2854.

［18］Powers D M W.Evaluation：from precision，recall and F-measure toROC，informed ness，marked ness and correlation［J］.Journal of Machine Learning Technologies，2020（2）：37-63.

收稿日期：2023-02-21；修回日期：2023-04-13

作者簡介：熊偉超（2002-），男，四川南充人，碩士研究生，主要研究方向為數據挖掘、智能計算；蔣瑜（1980-），男（通信作者），四川鄰水人，副教授，碩士，主要研究方向為數據挖掘、粗糙集與智能計算（jiangyu@cuit.edu.cn）．