基于人工智能的深潛耐壓球殼應力場映射

姚驥，汪雪良，葉聰，顧學康，孫夢丹，蔣鎮濤

（1.中國船舶科學研究中心，江蘇 無錫 214082；2.深海技術科學太湖實驗室，江蘇 無錫 214082）

深潛耐壓球殼是載人深潛器的核心部件，其結構安全是確保潛器順利完成水下任務的前提，因此對其結構健康狀態的實時監測十分重要。當前，由于安全條件、空間分布等限制，僅能對有限測點的應力信息進行實時監測，無法直接獲取深潛耐壓球殼全局應力場信息。因此，亟需開展利用有限測點信息，間接測量全局應力場信息的研究。

目前，許多學者針對深潛耐壓球殼結構的安全性與承載能力開展了大量研究。其中，挪威船級社（DNV）[1]、法國船級社（BV）[2]、美國船級社（ABS）[3]、俄羅斯船級社（RS）[4]和中國船級社（CCS）[5]均對載人艙球殼的承載能力設計進行了要求，要求極限承載能力至少應為最大工作壓力的1.5 倍以上[6]。張磊等[7]對不同計算公式的計算結果進行了對比，發現各公式預測結果與實驗破壞壓力均存在偏差。楊露等[8]通過實驗和數值計算方法，對大深度載人艙長期壽命評估中的影響因素開展了研究。王芳等[9-13]針對大深度載人潛器疲勞問題開展了研究，并在結構退化規律、疲勞壽命預測等方面取得了相關成果。王丹等[14]針對載人艙球殼本身初始形狀對其臨界載荷的影響開展了研究，并給出了計算表達式。楊華偉等[15]為保障載人艙球殼結構安全，開展了載人艙結構健康監測評估系統設計研究，并給出了結構安全性評估算法函數。在應力場監測與映射方面，李卿漢等[16]針對船海結構疲勞失效的問題，設計了一種基于應力測量和響應技術的船舶結構可靠性監測系統。周天宸等[17]利用BP 神經網絡和粒子群算法提出了一種船舶結構應力監測數據處理與異常診斷算法。姚驥等[18]利用人工智能方法提出了一種張力腿結構全局變形場映射方法。張濤等[19]以海洋平臺某連接器結構為研究對象，提出了一種基于BP 神經網絡的應力場求解方法，該方法求解精度達到93.6%。Kefal 等[20-21]運用逆有限元法對船舶結構典型位置的全局應力和彎矩進行了計算。張宏等[22]基于BP 神經網絡和粒子群算法，提出了一種油氣管道二維應力分布的機理模型。李成等[23]對不同荷載作用下圓孔板孔邊及孔口附近應力場開展了仿真分析，并建立了基于彈性理論及復變函數理論的計算模型。白茉莉等[24]基于復變函數方法，結合計算軟件的符號運算系統對橢圓形孔口周圍應力場進行了推導，并給出了全空間應力場的解析表達式。綜上所述，當前對于深潛耐壓球殼全局應力場映射研究較少。

圍繞深潛耐壓球殼全局應力場實時映射這一核心問題，本文提出一種基于人工智能的深潛耐壓球殼應力場映射模型。首先，基于球殼設計參數、建造過程數據、模型試驗數據，構建深潛耐壓球殼有限元模型，并開展仿真分析。其次，綜合考慮應力分布形式、相互獨立性、安裝條件等因素，提出深潛耐壓球殼監測布點方案。然后利用長短時記憶神經網絡（Long-short Term Memory Network，LSTM），將測點應力信息作為輸入，將全局應力場信息作為輸出，構建了深潛耐壓球殼應力場映射模型，并與其他神經網絡方法進行對比。最后，對不同測點數量下的映射精度進行了驗證。

1 深潛耐壓球殼簡介與仿真分析

1.1 深潛耐壓球殼

深潛耐壓球殼主要由球殼、開口1 及開口2 等部件組成，如圖1 所示。在長期服役過程中，經常在工作深度范圍內上浮和下潛。當深度發生變化時，球殼承受的外部壓力也不斷變化。因此，對其結構狀態的實時監測十分重要。

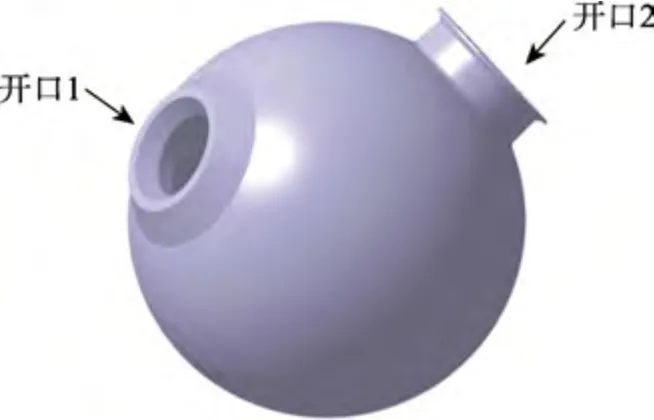
圖1 深潛耐壓球殼示意圖Fig.1 Schematic diagram of deep-sea pressurized spherical shell

深潛耐壓球殼主要由高性能鈦合金組成，該材料具備屈強比高、潛深大、服役年限長、下潛往復次數多等顯著特征。表1 給出了深潛耐壓球殼的相關參數，其中厚度t的計算見式（1）—（3）。

表1 深潛耐壓球殼結構參數Tab.1 Structural parameters of deep-sea pressurized spherical shell

式中：Pj為計算載荷；R為球殼內部半徑，取396 mm。因此，球殼厚度t=33.33 mm。為安全考慮，t取35 mm。

1.2 深潛耐壓球殼仿真分析

深潛耐壓球殼在長期服役過程中，主要承受靜水壓力的作用。因此，利用有限元方法構建深潛耐壓球殼仿真模型，其中開口1 與開口2 處采用等效載荷方式。其次，根據中國船級社《潛水系統和潛水器入級規范》要求，采用3 點約束的方式，約束6 個位移分量，邊界條件對稱設置，即在殼體位于x和z坐標軸的位置上（相隔90°）取3 個節點：在z軸上的節點1 和2，其ux=uy=0；在x軸上的節點3，其uy=uz=0。

深潛耐壓球殼有限元仿真結果如圖2 所示，其中仿真模型選用六面體單元，網格尺寸為2 cm。可以看出，在開口1 與開口2 處均存在高應力區。同時，球殼典型位置處應力分布較為均勻。

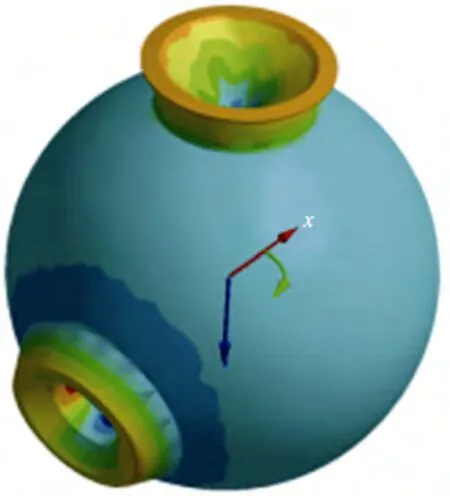
圖2 深潛耐壓球殼有限元仿真云圖Fig.2 Simulation cloud map of deep-sea pressurized spherical shell

將仿真結果與模型試驗結果進行對比，結果見表2。可以看出，最大誤差僅為1.92%。說明有限元分析結果較為準確，可為深潛耐壓球殼應力場映射算法提供數據支撐。

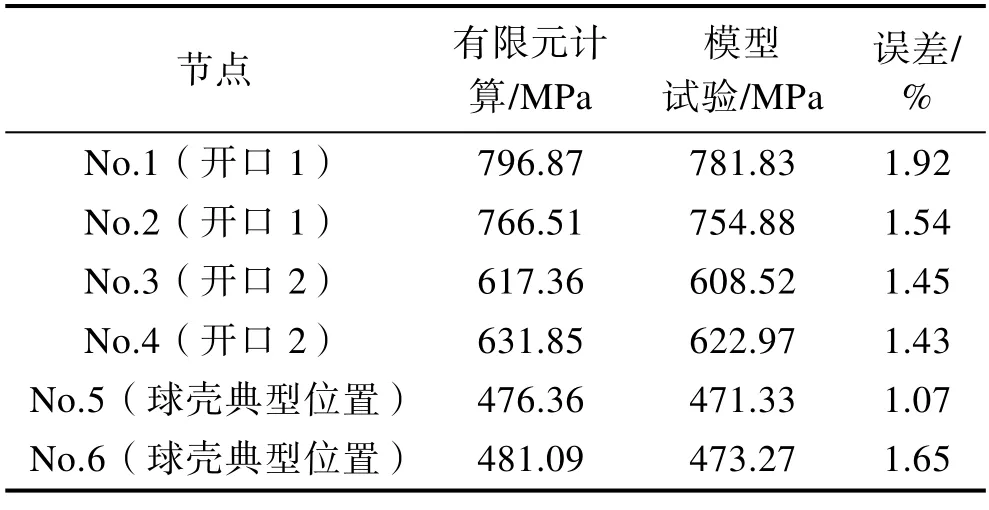
表2 仿真結果與試驗結果對比Tab.2 Comparison between simulation results and experimental results

1.3 監測布點方案決策

深海耐壓球殼應力場成因復雜，影響因素多，現有測量手段往往只能反映局部應力的信息。綜合考慮應力分布形式、相互獨立性、安裝條件等因素，在開口1、開口2 等高應力區位置及赤道焊縫處各選取8 個測點，球殼典型位置處選取6 個測點。利用人工智能方法，構建測點應力與全局應力場的映射關系模型。

2 應力場映射算法研究

2.1 數據集選取

選取載荷步為0.1 MPa，對設計載荷（100 MPa）進行劃分，并開展有限元仿真，共仿真1 000 個工況。將測點應力作為輸入，將全局應力場作為輸出，構建球殼應力場映射模型。此外，訓練集、交叉驗證集與檢驗集的比例分別為70%、15%、15%。應力場影響映射算法數據集選取見表3。

表3 數據集選取Tab.3 Selection of datasets

2.2 長短時記憶神經網絡（Long-short Term Memory Network，LSTM）

與標準神經網絡相比，循環神經網絡是以序列數據為輸入、在序列演進方向進行遞歸，且所有節點按鏈式連接的遞歸神經網絡，可將上一個狀態的信息傳遞到當前狀態。當輸出為時間序列時，可以將其展開為一系列相互連接的標準神經元。LSTM 神經網絡是循環神經網絡的一種，用以解決一般循環神經網絡中存在的長期依賴問題。LSTM 神經網絡結構由Hohreiter 和Schmidhuber 于1997 年提出[25]，是一種特殊的循環神經網絡，由一系列LSTM 元組成，如圖3 所示。

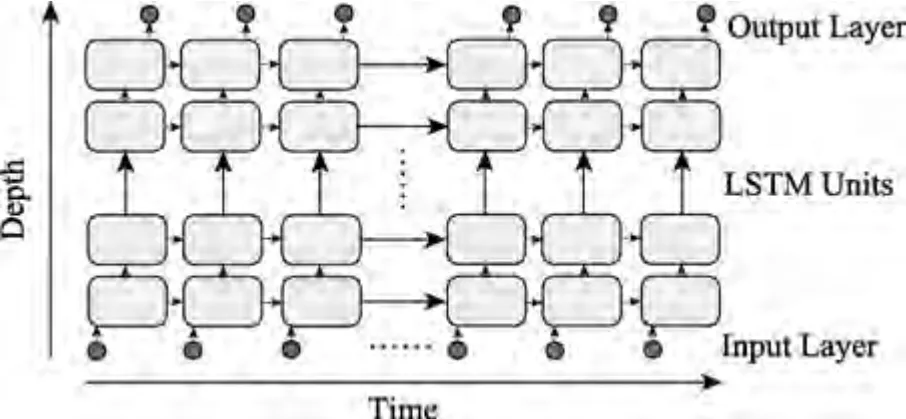
圖3 LSTM 結構Fig.3 LSTM structure

LSTM 元包括新輸入xt、輸出ht、輸入門it、忘記門ft、輸出門ot，如圖4 所示。引入輸入門、忘記門與輸出門的目的是控制每一步輸出的值，使得誤差在該神經元傳遞過程中保持不變。LSTM 是循環神經網絡的一個特例，新輸入和每個門都會將前一次的輸出ht－1作為本次輸入的一部分。因此，新輸入xt、輸入門it、忘記門ft、輸出門ot的輸入都是由[xt,ht－1]二元組構成。

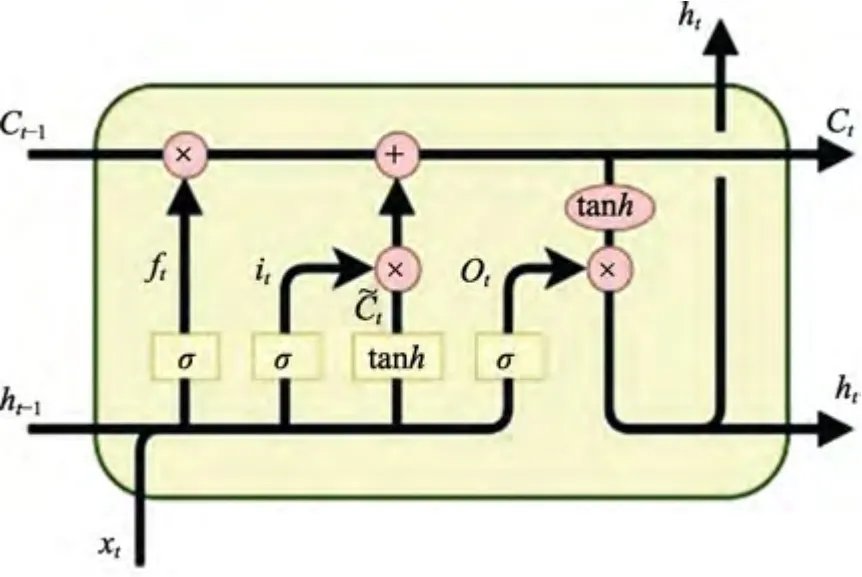
圖4 LSTM 循環體結構Fig.4 LSTM loop structure

新輸入[xt,ht－1]經過激活函數σc作用后，得到記憶元的候選值Ct：

式中：Wc表示連接權；bc表示激活函數的一個激活閥值。

輸入門用于調整候選值Ct的大小，輸入門的輸出為：

式中：Wi表示連接權；bi表示激活函數的一個激活閥值。候選值Ct經過輸入門的調整，其值為Ct·it。

忘記門用于控制LSTM 元的記憶狀態St－1，忘記門的輸出為：

式中：Wf表示連接權；bf表示激活函數的一個閥值。記憶狀態St－1經過忘記門的調整，其值為ft·St－1。

此時，t時刻的狀態St由其所記憶的前一時刻狀態St－1和狀態更新的候選值加權得到:

輸出門ot當作狀態St最終輸出的一個權值，控制狀態St的輸出大小，輸出門的公式為：

最終LSTM 元的輸出為：

式中：σc、σi、σf、σo、σs為激活函數。

2.3 建模過程

LSTM 應力場映射模型如圖5 所示。整個深度學習模型共包括6 層，其中LSTM 層數為2，每層節點數為10，全連接層數為2，節點數為10，最后一層作為輸出層。采用均方根誤差作為代價函數，訓練次數為1 000。

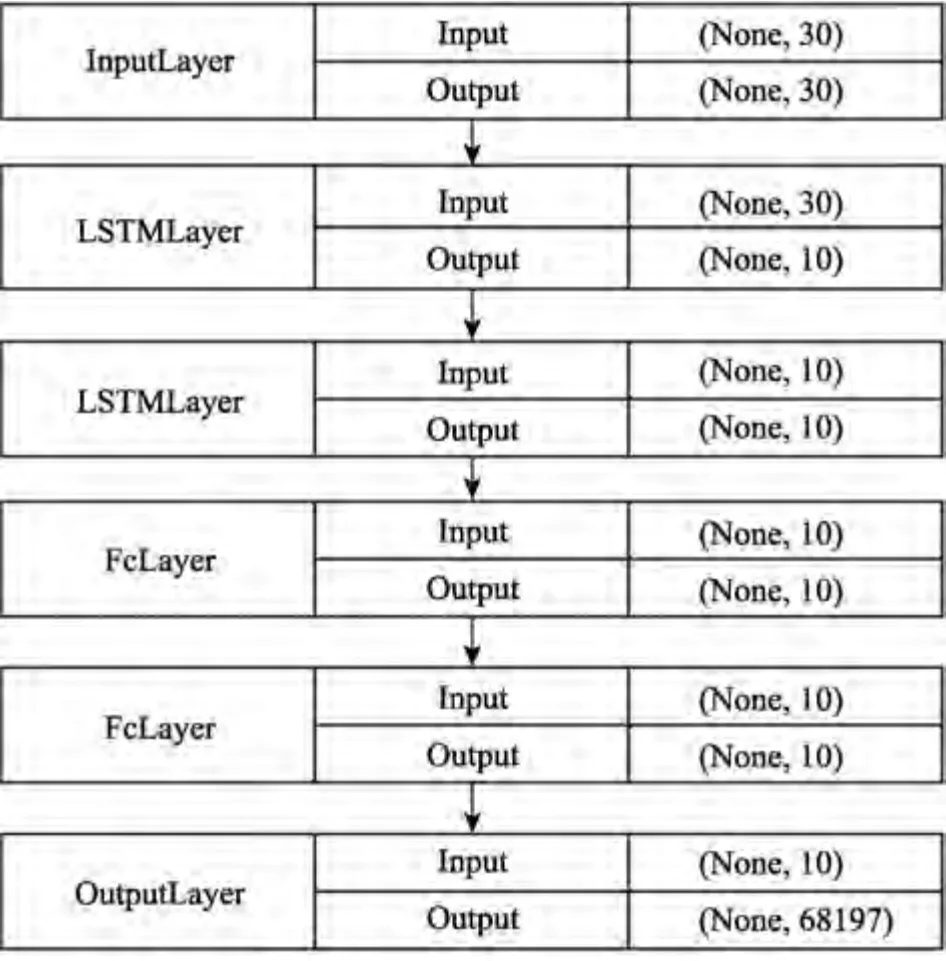
圖5 應力場映射模型Fig.5 Stress field mapping model

3 結果分析與討論

3.1 映射結果分析

深海耐壓球殼應力場映射算法的訓練過程如圖6所示。可以看出，隨著訓練次數的增加，訓練損失值與交叉驗證損失值降低，兩者具備較好的一致性。同時，訓練均方根誤差與交叉驗證均方根誤差隨著訓練次數的增加而降低。在訓練完成時，訓練損失值為2.42，交叉驗證損失值為9.44，訓練均方根誤差為2.20，交叉驗證均方根誤差為4.34。

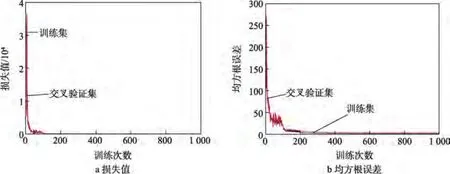
圖6 訓練過程Fig.6 Training process:a) loss;b) RMSE

不同深度下全局應力場的映射結果如圖7 所示，其中下潛深度選取1 000、4 000、7 000、10 000 m。可以看出，在下潛深度較小時，映射結果與期望結果存在一定的偏差，其線性擬合斜率為0.99，接近于1。當下潛深度增大時，映射結果與期望結果具備較好的一致性，其線性擬合斜率均為1。相比應力場變化范圍，其在y軸上的截距較小，進而說明本文所提深潛耐壓球殼應力場映射算法具備較好的映射精度。

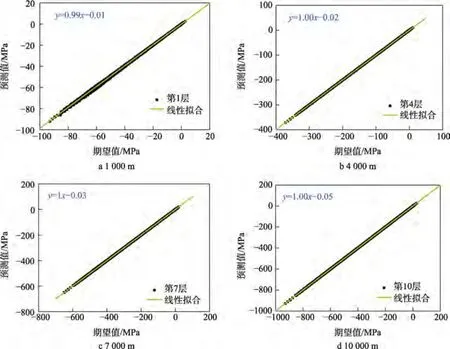
圖7 不同下潛深度的映射結果Fig.7 Mapping results of different diving depths

為了進一步分析LSTM 模型的映射準確率，圖8給出了所提模型的映射殘差Rs：

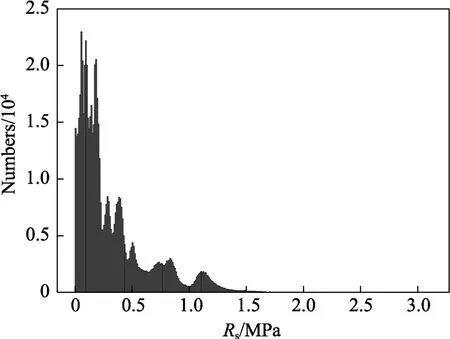
圖8 映射殘差分布Fig.8 Distribution of mapping residual error

可以看出，映射殘差大多分布在0～0.5 MPa。相比于應力場的變化范圍，映射殘差極小。

為了定量分析所提模型的映射誤差，選取平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）ηMAPE作為評價指標：

深潛耐壓球殼應力場映射模型的映射誤差（±表示偏差方向）如圖9 所示。可以看出，在下潛深度較小時，映射結果與期望結果相對誤差為－1.49%。當下潛深度增大時，映射誤差較小，均小于0.5%。在下潛深度為10 000 m 時，映射誤差僅為0.05%。映射結果表明，本文所提深潛耐壓球殼應力場映射算法可對其下潛過程中的全局應力場進行準確映射，并具備較高精度。

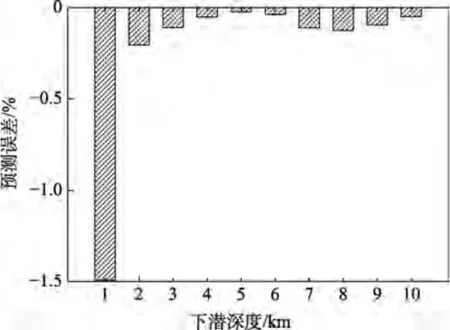
圖9 不同下潛深度的映射誤差Fig.9 Mapping error under different diving depths

此外，利用相同計算資源（i7-10700CPU@2.9 GHz,32RAM,NVIDIA GeForce RTX 2060）開展研究。有限元模型計算1 個工況平均耗時為1.2 s，而本文所提應力場映射模型計算 1 個工況平均耗時0.019 6 s，計算效率提升約60 倍，為深海耐壓球殼在實際服役過程中的應力場實時映射提供支撐。

3.2 不同方法映射結果對比

為了評估本文所提深潛耐壓球殼應力場映射算法的精度，選取深度神經網絡（Deep Neural Network，DNN）與反向傳播算法（Back Propagation，BP）作為對比，構建深潛耐壓球殼應力場映射模型。其中DNN 模型隱藏層數為3，各層節點數為30。BP 模型隱藏層數為1，節點數為50。損失函數選取與LSTM模型一致。

不同模型不同下潛深度下的映射結果如圖10 所示。可以看出，相比LSTM 模型，DNN 模型與BP模型均存在較大的映射誤差。其中，BP 模型在下潛深度較小時，映射結果較差。當下潛深度增加時，映射誤差減小。

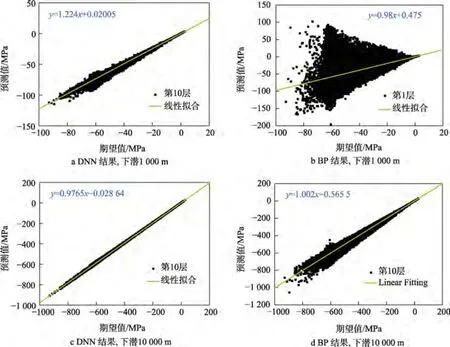
圖10 不同模型的映射結果Fig.10 Mapping results of different models:a) DNN results,1 000 m;b) BP results,1 000 m;c) DNN results,10 000 m;d) BP results,10 000 m

為了定量分析不同模型的映射精度，圖11 給出了不同模型不同下潛深度下的映射誤差。可以看出，BP 模型的映射誤差最大，在下潛深度較小時達到了50%以上；DNN 模型的映射誤差小于BP 模型，大于LSTM 模型，在下潛深度較小時達到20%以上；LSTM 模型映射誤差最小，且遠小于DNN 模型與BP 模型。

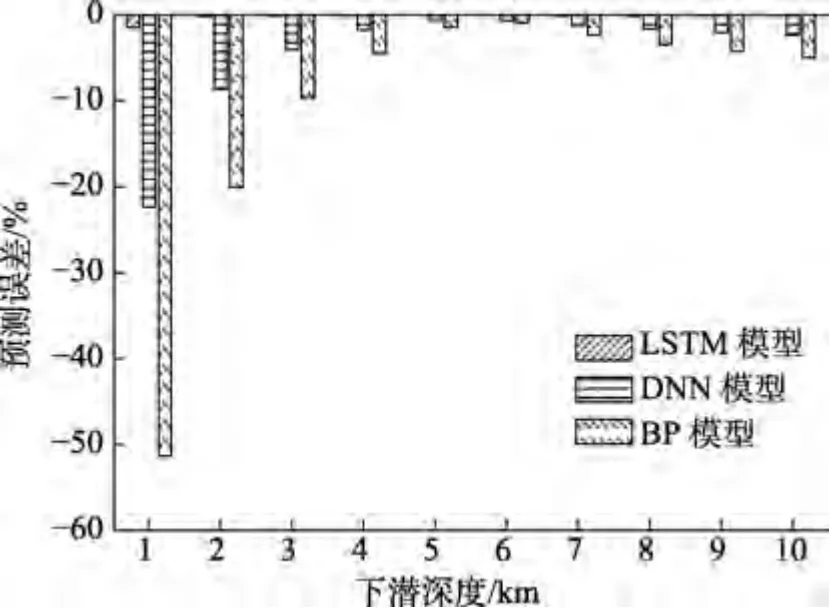
圖11 不同模型不同下潛深度映射誤差Fig.11 Mapping errors of different models under different diving depths

由不同模型的映射誤差可知，LSTM 模型的平均映射誤差為0.23%，相比于DNN 模型與BP 模型的4.53%和 10.30%，映射誤差分別下降 94.92%與97.76%。這進一步說明了本文所提模型可對實際下潛過程中深潛耐壓球殼全局應力場進行實時映射。

3.3 不同監測數量下的映射結果

在深潛耐壓球殼長期服役過程中，傳感器容易發生機械故障，導致設備失效。此外，失效點存在隨機性。因此，采用隨機丟失的方式，選取監測點數量為5、10、15、20、25、30（無丟失），利用所提深潛耐壓球殼應力場映射算法，構建不同監測數量下的耐壓球殼應力場映射模型。

不同監測數量下，相同下潛深度（10 000 m）的映射結果如圖12 所示。可以看出，在所選監測數量（5、10、15、20、25、30）下，各映射模型的映射結果與實測結果均保持較好的一致性，其線性擬合斜率均為1。同時，相比應力場變化范圍，其在y軸上的斜率較小。

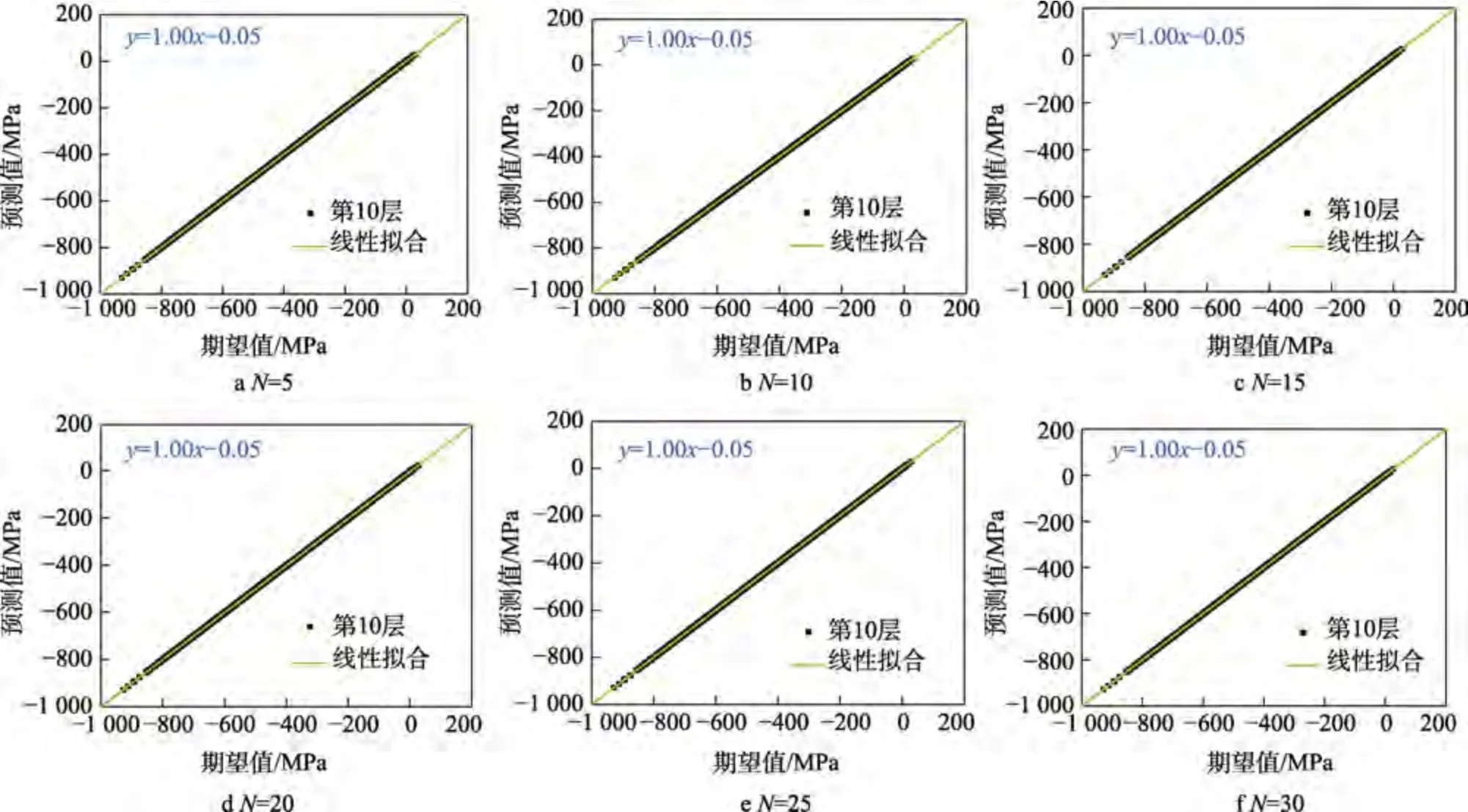
圖12 不同監測數量下的映射結果Fig.12 The mapping results of different monitoring locations

為了定量分析不同模型在不同下潛深度時的映射結果，圖13 給出不同監測數量下各模型在不同下潛深度下的映射誤差。可以看出，在下潛深度較小時，各模型的映射誤差較大，但也均小于1.5%。在下潛深度較大時，各模型映射誤差均小于0.5%。

圖13 不同監測點下不同深度的映射誤差Fig.13 The mapping results of different depths of different monitoring locations

由不同監測數量下的映射誤差可以看出，監測數量為5 時，映射誤差為0.17%，監測數量為30 時，映射誤差為 0.23%，所提模型的映射誤差均小于0.5%。所提深潛耐壓球殼應力場映射算法可在測點存在部分失效的情況下仍取得較高的映射精度，同時驗證了所提監測布點方案具備監測冗余性。

4 結論

本文提出一種基于人工智能的深潛耐壓球殼應力場映射算法，解決了實際下潛過程中全力應力場難以獲取的問題，也為耐壓結構受力狀態全方位監測提供新的思路。主要結論如下：

1）基于深潛耐壓球殼建造過程數據，建立高保真的有限元模型，并與模型試驗數據進行對比，最大誤差僅為1.92%。給出了深海耐壓球殼應力監測方案。

2）基于LSTM 網絡，構建深潛耐壓球殼應力場映射模型。從映射結果可以看出，其全局應力場最大誤差僅為1.49%。與有限元仿真計算相比，所提方法的計算效率提升約60 倍。

3）針對實際服役過程中潛在的傳感器失效風險，采用隨機丟失的方式，對不同監測數量的映射模型進行分析。所提方法平均誤差均小于0.5%。