基于改進灰色馬爾可夫的港口貨物 吞吐量預測研究
丁天明,潘 寧,杜柏松,艾萬政
(浙江海洋大學 船舶與海運學院,浙江 舟山 316022)
0 引 言
港口貨物吞吐量決定著港口資源分配的效率,直接影響著港口發展規劃的合理性、科學性與先進性。對未來港口的長期發展規劃和決策來說,預測是至關重要的一步[1],因此提高港口貨物吞吐量的預測精確度就顯得尤為重要。目前對吞吐量的預測方法有時間序列[2]、概率統計[3]、指數平滑[4]、灰色理論[5]、支持向量機[6]、神經網絡[7]以及組合預測等。其中,組合預測方法應用較多:李長安等[8]將反向傳播神經網絡模型在蟻群算法的改進下進行吞吐量預測,加快了原始模型的收斂速度,提高了預測的精度,但是當數據不充分時,神經網絡處于失效狀態,因此該算法還有待提高;徐勇[9]通過灰色理論構建了原始預測模型,在分析吞吐量時間序列的趨勢之后,實現了其精準預測的目的;TANG Shuang等[10]選取了5種影響因素,使用數據集建立多元線性模型和反向傳播神經網絡模型分別對上海港和連云港進行了預測評估;翁志堅等[11]針對灰色系統在預測有較大波動的數據序列過程中存在的缺陷,在馬爾可夫理論基礎上建立了新維灰色預測模型;王振振等[12]將各季度影響吞吐量的程度用加權灰色關聯分析進行了排序,再結合三次指數平滑法與馬爾科夫模型,大幅度提高了預測精度。
由于港口貨物吞吐量的樣本數據相對較少,信息量較匱乏[13],給預測過程帶來了一定的難度,而灰色模型對樣本數據沒有過高的要求,可以以簡便的方式運用小規模數據對非平穩隨機過程進行預測并反映出序列的長期發展趨勢,因此該模型目前在吞吐量預測方向的應用最為廣泛[14-16]。但灰色模型在處理有波動性的數據時存在一定的缺陷,而馬爾可夫過程能很好地解決這一問題,且其具有無后效性的特點,因此筆者用一階馬爾可夫鏈對模型殘差進行修正,用以彌補灰色預測的誤差精度。然而在目前的馬爾可夫狀態區間劃分過程中均以中間值作為狀態區間的白化系數,并沒有隨著實際區間的改變而調整。因此,筆者在馬爾可夫修正的過程中還提出用粒子群算法對狀態區間劃分的參數因子進行動態優化,使其能自主適應區間數值的變化、及時更新馬爾可夫鏈的每個狀態區間系數并達到最優修正值。筆者將吸收以上3種模型算法的優點,通過粒子群算法迭代尋優,分別找到各區間最合適的白化系數,改進灰色馬爾可夫預測模型,對比分析得到較高精度的吞吐量預測值。
1 基于貨物吞吐量的模型建立
1.1 建立灰色預測模型
令非負原始時間序列為X(0)={x(0)(1),x(0)(2),…,x(0)(n)},經過一次加和生成后取得一階加和總序列X(1)={x(1)(1),x(1)(2),…,x(1)(n)}。
建立灰色GM(1,1)一階預測模型:
(1)
式中:參數a和b分別反應了模型的增長速度和協調變換關系。
此時模型對應的解用最小二乘法求解得到:
(2)
B和Yn表達式如式(3)、式(4):
(3)
(4)
令初始條件為x(1)(1)=x(0)(1),得出微分方程的解為:
(5)
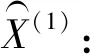
(6)
再將模擬值進行累減計算,得到原始數據的預測值:
(7)
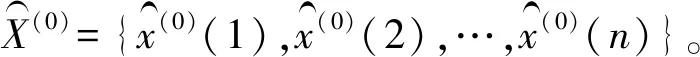
1.2 馬爾可夫修正
馬爾可夫鏈主要研究狀態之間可能存在移動性的概率關系,事物的發展只與當前狀態有關,與其他狀態無關[17]。由于原始序列具有一定的波動性和隨機性,使得GM(1,1)預測模型在實踐過程中存在一定的誤差。筆者用一階馬爾可夫對灰色預測模型進行殘差修正,最大程度上克服了原始模型在數據波動上的局限性。馬爾可夫鏈的特點是客觀事物下一步的狀態只與當前狀態有關聯,與除當前之外的所有狀態均無關,即:
p′(Xt+1=j|Xt=i)=p′(Xt+1=j|Xt=it,Xt-1=it-1,…,X0=i0)
(8)
式中:Xn∈Ej,對任意的t∈E,i∈E,其中,E為等分區間集合,Ej為第j個等分區間。
由灰色系統理論得到的預測值可計算出與原始序列值的相對殘差:
(9)
根據相對殘差的大小來劃分修正狀態區間,每個區間的間隔相同,將其平均劃分等分區間Ei=[Li,Ui],最后建立一階狀態轉移矩陣Pij。該矩陣反映了各個殘差狀態區間移動過渡的可能性,即當前狀態移動到下一個狀態的概率:
(10)

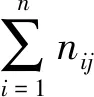
Pij(m)=[Pij(1)]m
(9)
得出灰色馬爾可夫預測模型如式(12):
(12)
其中,預測狀態“高估”時取正,“低估”時取負。
1.3 粒子群優化白化系數
對于傳統的灰色馬爾可夫組合模型,狀態區間取中值0.5未必為最優狀態。筆者引進粒子群算法(particle swarm optimization, PSO)代替模型中直接取中值的方式,對馬爾可夫模型各個狀態i的參數因子進行優化。將白化系數λi帶入灰區間求解:
Ii=λiLi+(1-λi)Ui
(13)
式中:λi∈[0,1];Li、Ui分別為狀態區間的上、下邊界值。
PSO算法是一種復雜適應優化算法,具有參變量少、全局搜索能力強、收斂速度快等優點[18]。其為一群隨機的粒子在搜索空間上通過合適的速度不斷地尋優迭代,找到最適合所有粒子的最佳位置,此時為最優解。而這些粒子均具有確定其好壞的功能,即適應度函數,在滿足這個函數之后才能繼續向前搜索。取m個粒子組合成一個群集,其中任一粒子q在d維空間中均有D維向量,每個向量均代表一個白化因子λq,每個粒子q均在空間里以速度vqd進行搜索,其搜索的位置xqd和速度vqd不斷更新迭代,表達式為:
(14)
(15)
式中:學習因子c1和c2能夠提高模型的收斂速度且避免陷于局部最優;r1和r2為[0,1]之間的隨機數;w為慣性因子,可以使局部和全局搜索能力達到均衡;pbest,qd、gbest,qd分別為個體極值點、全局極值點的位置。
筆者用誤差的均方差值eMS來衡量每個粒子優劣程度的適應度函數,此時均方差值越小越好。粒子適應度函數的表達式為:
(16)
基于PSO算法改進的灰色馬爾可夫復合預測模型流程如圖1。
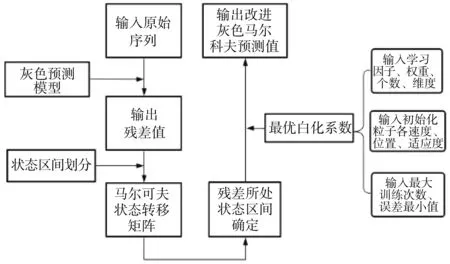
圖1 基于粒子群優化的灰色馬爾可夫貨物吞吐量預測模型流程
算法步驟如下:
1)輸入原始預測序列到灰色GM(1,1)模型中,得到殘差值。
2)將殘差值進行區間等概率劃分并建立一階狀態轉移矩陣。
3)根據狀態轉移概率矩陣確定各年份所處的狀態區間。
4)輸入粒子群算法的各項參數值并開始迭代運算,獲取各區間的白化系數。
5)輸出粒子群改進后的最終預測值。
1.4 精度分析
筆者通過對比分析各模型的方差比值和小殘差概率值來判斷各模型的預測精度。首先將預測數值與實際數值相減并取絕對值,得到絕對殘差序列:
(17)
設原始序列X(0)的均方差為S1,殘差序列Δ(0)的均方差為S2,方差比為二者比值:
(18)
小殘差概率:
(19)
方差比值C越小表示當原始序列均方差S1相等的情況下,該模型的殘差序列均方差S2越小,此時該預測模型殘差飽和度小,精度高。小殘差概率pr越大表示殘差與殘差平均值之差中小于原始定值0.674 5倍的數值越多,精度也越高,其精度判別見表1。
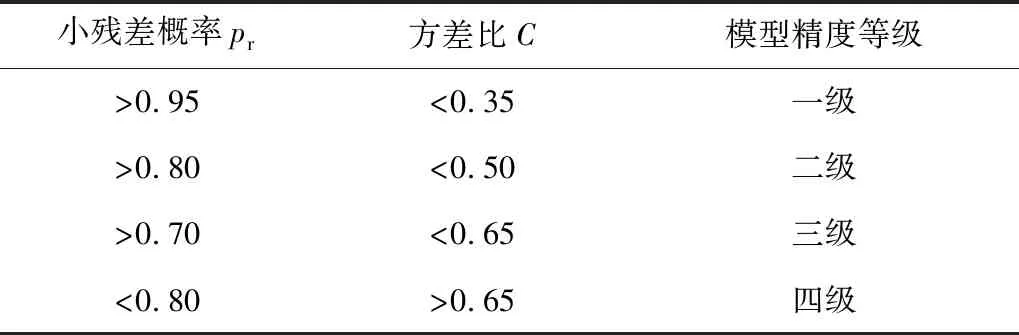
表1 后驗差檢驗判別參照
2 實例應用
選用《中國統計年鑒》中2007—2021年寧波舟山港的港口貨物吞吐量(表2)作為研究對象進行分析。分別將傳統的灰色預測、灰色馬爾可夫復合預測和粒子群優化的灰色馬爾可夫這3種預測模型進行比較,找出最優精度的模型并預測未來3 a吞吐量情況,為后續港口生產建設提供理論依據。

表2 寧波舟山港2007—2021年貨物吞吐量
2.1 GM(1,1)預測
由表2可以看出,寧波舟山港港口貨物吞吐量總體呈平穩增長趨勢。
將表2中數據進行累加得到一階累加序列X(1)={47.336,100.284,157.968,221.268,290.661,365.062,446.040,533.386,622.315,714.524,815.457,923.896,1 035.905,1 153.145,1 275.55}。將此數據帶入式(1),得到a=-0.060 4,b=53.062 2。進而一階微分方程的解為:
(20)
從式(20)得出灰色預測的一階累加序列模擬值,對其進行累減,即可得到原始序列對應的模擬預測序列和相對殘差值,見表3。
2.2 灰色馬爾可夫預測
根據表3中的殘差序列,采用等概率方法對其進行狀態劃分,具體區間分為以下4個狀態:極度高估E1、高估E2和E3、較為準確E4,其中每個狀態區間誤差間隔為3.5%,區間劃分見表4。

表4 狀態區間劃分
根據各年殘差值落入的狀態區間劃分各年份的狀態。E1:2008,2009;E2:2010,2021;E3:2007,2011,2012,2015,2016,2019,2020;E4:2013,2014,2017,2018。
此時由式(11)建立一階狀態轉移矩陣:
根據狀態轉移矩陣和各年份所處狀態區間,將各年份的灰色預測值由式(12)進行修正,得出灰色馬爾可夫復合模型的預測值,見表5。
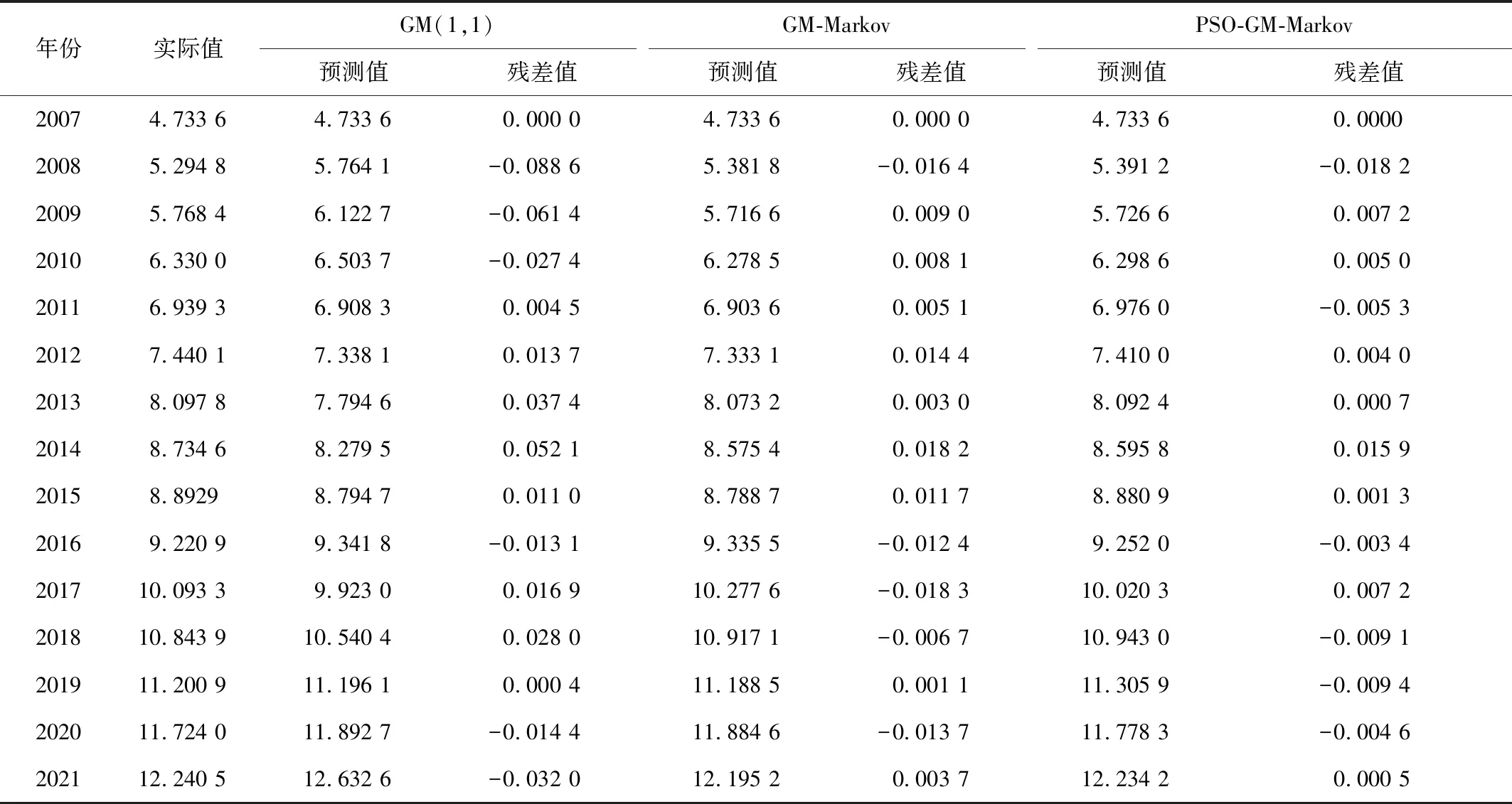
表5 寧波舟山港貨物吞吐量3種模型預測對比
2.3 優化灰色馬爾可夫預測
將2.2節中經過劃分的4個殘差狀態區間視為灰區間,將這些灰區間的白化系數代入粒子群算法〔式(14)〕得到:
I1=λ1×(-0.088 6)+(1-λ1)×(-0.053 5)
(15)
I2=λ2×(-0.053 5)+(1-λ2)×(-0.018 3)
(16)
I3=λ3×(-0.018 3)+(1-λ3)×0.016 9
(17)
I4=λ4×0.016 9+(1-λ4)×0.052 1
(18)
而傳統的灰色馬爾可夫組合模型實際上是將其取中間值,即λi=0.5,i=1,2,3,4。事實上此4個區間狀態并非均取中值。筆者利用粒子群算法迭代搜尋各狀態區間實際參數,優化式(15)~式(18)的組合模型,確定當下合適的白化因子。
經過多次調試,取參數粒子長度為4,最大種群數為1 000,學習因子c1=0.6,c2=0.8,權重w=0.8,粒子最大更新位置為1,最小為0,更新速度最大、最小值分別為0.01、 -0.01。利用1.3節中粒子群算法的具體步驟,在MATLAB軟件上運行程序得到優化后的動態白化系數λ={0.069 1,0.032 6,0.009 7,0.036 8}。由此可見,每個狀態區間的系數取中間值0.5并不能達到最優預測效果。將優化后的λ值分別代入灰色馬爾可夫組合預測模型,各狀態區間進一步得到改進后的預測值見表5。
2.4 精度分析
對3種預測模型進行誤差和后驗差檢驗,如表6。由表6可知:3種模型的精度等級均為一級;相較于灰色GM(1,1)預測模型,灰色馬爾可夫組合模型精度進一步提高,平均誤差均值降低了62%;經粒子群改進灰色馬爾可夫后的C值最小,精度也最優,平均誤差均值下降了76%,相較于灰色馬爾可夫組合模型下降了37%,這說明了經過二次修正后模型的擬合度更高。從圖2中也可直觀地看出,粒子群優化灰色馬爾可夫模型的預測值與實際值更為貼合。因此,在馬爾可夫修正模型中,參數直接取中間值的方法存在一定誤差,而粒子群算法很好地克服了此模型的不足。
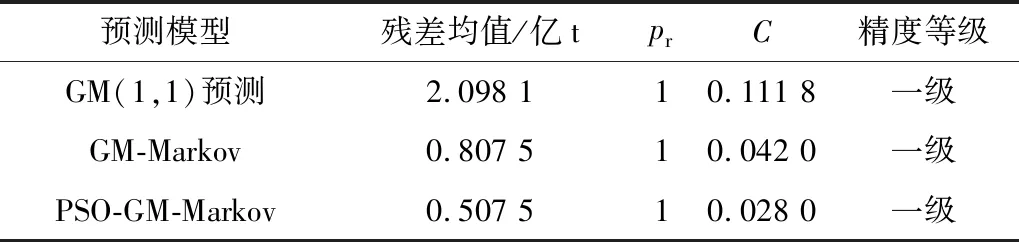
表6 模型精度對比
2.5 寧波舟山港未來三年貨物吞吐量預測
首先對寧波舟山港的2022年貨物吞吐量值進行預測,由式(11)可得到灰色馬爾可夫組合模型的n步轉移矩陣。同時選用與預測年份相隔最近4 a的轉移步數和所在狀態,建立狀態轉移矩陣,計算得到2022年的累積狀態轉移概率,如表7。從而確定2022年所處狀態區間,最后根據狀態區間劃分(表4)和動態白化系數預測寧波舟山港未來貨物吞吐量。

表7 2022年貨物吞吐量狀態預測
從表7可以看出,2022年累積狀態轉移概率最大為2.40,處于狀態區間E3中,因此對應的區間參數為λ3。結合式(12)、式(13)可以得到2022年的吞吐量預測值,同理可得寧波舟山港2023年和2024年的貨物吞吐量預測值,見表8。

表8 2022—2024年寧波舟山港貨物吞吐量預測值
3 結 語
1)筆者選用易于實施的粒子群算法,對灰色馬爾可夫模型在狀態區間參數選擇上的不足進行了改進。該算法影響參數較少,收斂速度快且具有良好的搜索能力,提高了模型的實用性。基于PSO算法改進后的灰色馬爾可夫模型在殘差均值上有一定幅度的下降,預測序列與原始序列基本擬合,很大程度上提高了復合模型的精確度,實現了對吞吐量的精準預測,為相關部門在港口規劃和布局上提供了一定的參考價值。
2)筆者在用一階馬爾可夫鏈修正灰色殘差值時,對狀態的劃分采用區間等分法,這直接影響到狀態轉移概率矩陣的確定,從而波及整個預測模型的精度。因此,可以對狀態區間的劃分做進一步改進,以期能夠提高預測精度。

