基于LSTM-EMD 模型的船舶航跡預測方法?

王均剛 胡柏青 高端陽 朱九鵬

（1.海軍工程大學電氣工程學院 武漢 430033）（2.大連艦艇學院航海系 大連 116018）

1 引言

隨著我國海洋事業的發展，海上航行的船舶數量日益增大，但與此同時也產生一系列新的問題，如狹窄水域堵塞情況頻發、船舶碰撞風險提高等，且航行中的船舶易受天氣影響而偏離航線，同樣會對船舶造成重大安全威脅，因而需要對船舶運動軌跡進行一定的預測，方便交通管理、船舶避碰以及保持正確航線，因此，提高船舶軌跡預測的精準度十分必要。

船舶軌跡預測是根據船舶的歷史軌跡數據及其他航行信息建立模型，對船舶下一時刻或接下來一段時間的軌跡進行預測，因此設計合適的預測模型對于軌跡預測至關重要。針對航跡預測模型的設計問題，GUO 等首先利用k階多元馬爾可夫鏈及相關參數建立一個狀態轉移矩陣，然后根據上一時刻概率最大的狀態對漁船下一時刻可能的軌跡進行預測，方法很有創新性，但忽略了對船舶歷史軌跡每一個狀態的考慮［1］；Hexeberg 基于歷史數據，提出了一種用來預測船舶未來時刻位置的單點鄰域搜索算法，有效利用了歷史數據的規律性，在船舶避碰中取得了較好的效果，但不能處理航行船只較少的航線［2］；TONG 等提出一種基于馬爾可夫鏈和灰度模型的改進預測模型，對船舶彎曲航道的軌跡也有較好的效果［3］；Perera 等［4～5］利用建立了對船舶的檢測和跟蹤的人工神經網絡模型，創新地將擴展卡爾曼濾波與神經網絡相結合，實現了對船舶狀態和航行軌跡的預測；王艷鋒［6］利用支持向量機（Support Vector Machine，SVM）對目標水域的船舶航跡進行預測，但研究范圍僅限于橋區水域；茅晨昊等［7］提出一種高斯回歸的船舶軌跡預測模型，可以預測接下來一段時間的船舶軌跡路線；Nguyen［8］將自動識別系統數據轉換為時間序列組，利用循環神經網絡模型對時間序列的良好學習能力，預測未來時刻的船舶軌跡、航行目的地和到達時間并取得了較好的預測效果。Suo 等［9］利用聚類算法在大量軌跡中提取主要軌跡，消除了冗余數據的影響，建立深度學習和門循環模型預測船舶軌跡。上述文獻提供了多種船舶運動軌跡的預測模型，具有良好的借鑒意義。

船舶自動識別系統是集合了全球定位系統、岸基、船載傳感器為一體的助航系統，能夠實現鄰近船舶間的信息交互，記錄歷史數據。該系統可獲取經度、緯度、航速、航向角、時間、船舶呼號、吃水量等多維信息［10～12］，在海事搜救、船舶避碰、追蹤船只等領域有著不可替代的作用。利用AIS 的歷史數據建模，對船舶未來時刻的軌跡進行預測能有效提高航海安全。但大量研究表明，利用AIS 數據進行軌跡預測存在如下問題：1）存在大量不可用的冗余數據，影響模型建立。2）容易產生噪聲。3）時間間隔不同［13～14］。為了提高軌跡預測的精度，需要對AIS 數據進行一定的預處理，降低上述缺陷的影響。本文的軌跡預測方法，包含數據預處理、LSTM模型預測、EMD 分解、殘差預測及補償四個部分。數據預處理部分通過插值的方法降低噪聲和時間間隔的影響，然后建立LSTM-EMD 組合預測模型，通過分解補償的手段實現了船舶軌跡的精準預測。利用AIS 數據進行實驗，證明了所提方法的有效性。

2 經驗模態分解

經驗模態分解是由黃鍔等提出的一種自適應信號處理方法，被認為是頻譜分析的一個重大突破。該方法無需預先設定基函數，僅需根據數據自身的時間尺度特征進行信號分解，因此其在理論上可以應用于任何類型信號的分解，正是由于這樣的特點，EMD 在處理非平穩非線性數據上具有非常明顯的優勢［15］。

EMD 分解算法的基礎是把信號內的震蕩看作是局部的。對給定的一組原始時序數據x(t)，首先找出信號x(t)的所有極大值點和極小值點，對極大值進行插值擬合和得到x(t)的上包絡emax(t)，對極小值進行插值擬合和得到x(t)的下包絡emin(t)，計算上下包絡的均值得到均值序列m(t)：

此時可將m1(t)看作原始數據的低頻成分，用x(t) 減去低頻成分m1(t) 得到序列的高頻成分d1(t)：

一般來說，得到的d1(t)并不滿足本征模函數的條件，需要將d1(t)作為原始序列重復上述過程k次，直至達到篩分門限TS，如式（3）。TS用于篩分由極大值確定的上包絡和由極小值確定的下包絡均值是否趨近于零，一般取值為0.2～0.3［16］。

式中，d1k(t)表示重復上述過程k次后得到的高頻成分，即IMF。記c1(t)=d1k(t) ，即第一個IMF。在x(t)中減去c1(t)得到去除第一個本征模函數的序列r1(t)。重復上述過程n次，直到cn(t)小于預設誤差或rn(t)為單調函數。分解后得到n 個IMF 分量和一個殘差rn(t)，將原始數據x(t)表示為IMF和殘差序列之和的形式：

3 LSTM-EMD組合模型

傳統前饋神經網絡在處理時間序列的預測方面效果并不好，且無法有效抑制梯度爆炸問題［17～18］，循環神經網絡應運而生。為解決循環神經網絡中的梯度問題，Hochreiter 等在循環神經網絡基礎上提出了長短時記憶網絡的特殊神經網絡［19］。LSTM是一種經過改進的循環神經網絡，可以學習長期的記憶信息，工作結構如圖1 所示。AIS 數據包含時間信息，因此AIS 數據中的軌跡可以視為一組帶有時間信息的序列，可以通過循環神經網絡學習軌跡的特性來預測下一時刻的軌跡位置［20］。EMD 算法是一種應用十分廣泛的信號分解方法，本文綜合LSTM 與EMD 算法的優勢，利用EMD 算法將LSTM預測信號分解補償，結合二者優勢進行船舶軌跡預測，提出一種LSTM-EMD 船舶軌跡預測模型，軌跡預測流程如圖2所示。

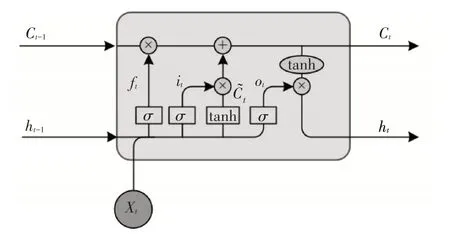
圖1 LSTM結構圖

圖2 LSTM-EMD組合模型預測流程圖

基于LSTM-EMD的船舶運動軌跡預測步驟如下：

1）LSTM 神經網絡訓練及預測。將船舶運動數據劃分為訓練集和測試集，根據經驗設置LSTM的隱含層節點數、迭代次數、學習率等參數，利用訓練集對神經網絡進行訓練。LSTM的輸入為當前時刻時間間隔、經緯度、航速、航向角等船舶信息，輸出為預測出的下一時刻船舶位置。訓練完成后，分別用訓練集和測試集進行預測，得到訓練集預測值和測試集預測值。

2）計算訓練集預測值與真實值的殘差序列res=Ytrue-，Ytrue為軌跡的真實值。

3）殘差序列分解。利用EMD 算法對殘差序列res進行分解，得到n個本征模態分量［IMF1,IMF2,...,IMFn］及殘差項rn。

4）本征模態分量的預測。對訓練集的res分解后得到n個IMF 及1 個殘差項rn。針對不同頻率的本征模態分量［IMF1,IMF2,...,IMFn］和殘差項rn分別建立LSTM 神經網絡進行訓練并預測，預測結果作為測試集預測值與真實值殘差的本征模態分量和殘差項，將預測結果求和，得到測試集殘差的預測值Yres。

5）預測結果。組合模型的預測結果為測試集預測值和測試集殘差預測值Yres之和，如式（5）。

4 模型驗證及分析

4.1 實驗方案及評價指標

本文采用應用廣泛的AIS 數據作為實驗數據，選取一組原始AIS 數據后，按照四個步驟進行實驗，而后進行實驗結果分析。為了充分證明實驗結果的有效性，本文選取傳統的BP 神經網絡模型和單一LSTM神經網絡模型的預測結果進行對比。

選用平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）、均方根誤差（Root Mean Square Error，RMSE）和誤差的標準偏差（Standard Deviation，SD）作為實驗的評價指標，MAPE、RMSE和SD越小表示預測效果越好。如式（6）～（8）所示。

式中，n為預測結果的數據個數，，yi分別為第i時刻軌跡的預測值和真實值。-yi為誤差，μ為平均誤差。

4.2 數據預處理

原始數據存在諸如數量級別相差較大、部分數據缺失等問題，若將其直接應用于神經網絡模型訓練，會因此類問題導致預測誤差增大，因此需要進行一定程度的數據預處理。數據預處理步驟如下：

1）增量處理。將原始數據處理為增量形式，可提高預測精度，將t 時刻的數據減去t-1 時刻的數據，即得到增量。

2）插值處理。AIS 數據的上傳與記錄是依托于GPS 信號，當遇到GPS 信號中斷或被屏蔽時，會使AIS 數據無法被連續采集而出現缺失值，而缺失值會對神經網絡模型的訓練產生一定負面影響，因此需要對缺失值進行插補，本文利用經典的拉格朗日插值法進行插補。

3）數據標準化。原始數據的最大值和最小值之間會出現較大的波動，波動導致神經網絡訓練和預測效果下降，因此采用標準差標準化的方法對數據進行標準化處理，標準化后的數據符合正態分布，表達式為

式中，x*為標準化后的數據，x為原始數據，xσ為數據標準差，xμ為數據平均值。處理后的數據之間邏輯關系不變，預測完成后的結果仍然是標準化數據，需要進行反歸一化處理才得到實際大小的數據。本文分別選取MMSI 為338158000、367628210在墨西哥灣航行的兩條軌跡作為原始數據，記為軌跡1、軌跡2，分別進行實驗。

4.3 LSTM訓練與預測

LSTM神經網絡的超參數是影響模型精度的重要因素，但目前并沒有嚴謹的、科學的公式確定超參數的大小，只有學者通過大量實驗總結出的經驗公式。本文采用控制變量法，逐步找到LSTM 神經網絡的最優參數，設置隱含層節點數為17，學習率為0.001，批處理數量為64，樣本訓練次數為300，輸入層為5，輸出層為2。以時間間隔Δtime、經度增量Δlon、緯度增量Δlat、航速增量ΔSOG和航向角增量ΔCOG五個特征量的數據作為輸入，以下一時刻的經度增量Δlont+1、緯度增量Δlatt+1作為輸出進行訓練與預測，并計算訓練集的預測值與實際值殘差。

4.4 EMD分解

將上一步中LSTM 模型預測得到的殘差進行EMD 分解，分解后得到多個不同頻率的本征模態分量以及一個剩余分量。以經度預測為例，將經度預測后的殘差進行EMD分解，得到6個本征模態分量IMF1-IMF6 以及一個剩余分量res，如圖3 所示，IMF1 為高頻部分，IMF7 為低頻部分，res 代表非線性趨勢。圖3中第一張圖片為EMD分解前的數據，下面6 張圖片分別為分解后的本征模態分量IMF1-IMF5，最后一張圖片為分解后的殘差res。

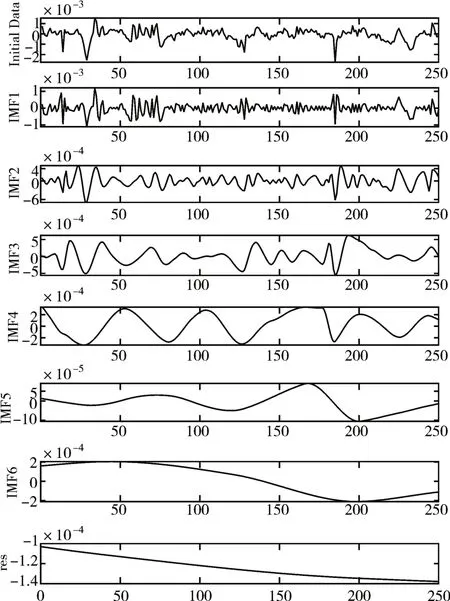
圖3 本征模分量圖

4.5 殘差預測及補償

分別建立LSTM神經網絡模型對各個IMF分量進行訓練并預測，得到測試集IMF 分量的預測值，將所有IMF 分量預測值求和后得到測試集的殘差預測值，根據式（4），相應的預測結果與殘差預測值相加，就完成了殘差的補償。兩組實驗數據的殘差預測結果分別如圖4～圖5 所示。由于殘差的隨機性和復雜度較大，因此很難完全準確地預測殘差，只能在整體趨勢上進行預測和補償，圖4～圖5已經表現出一定的預測效果。

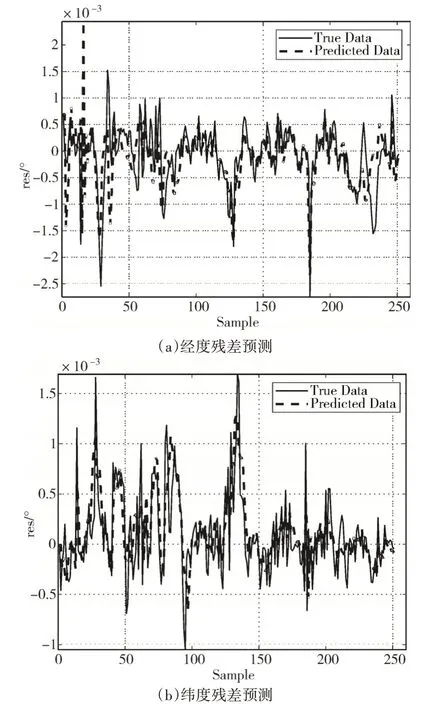
圖4 軌跡1殘差預測

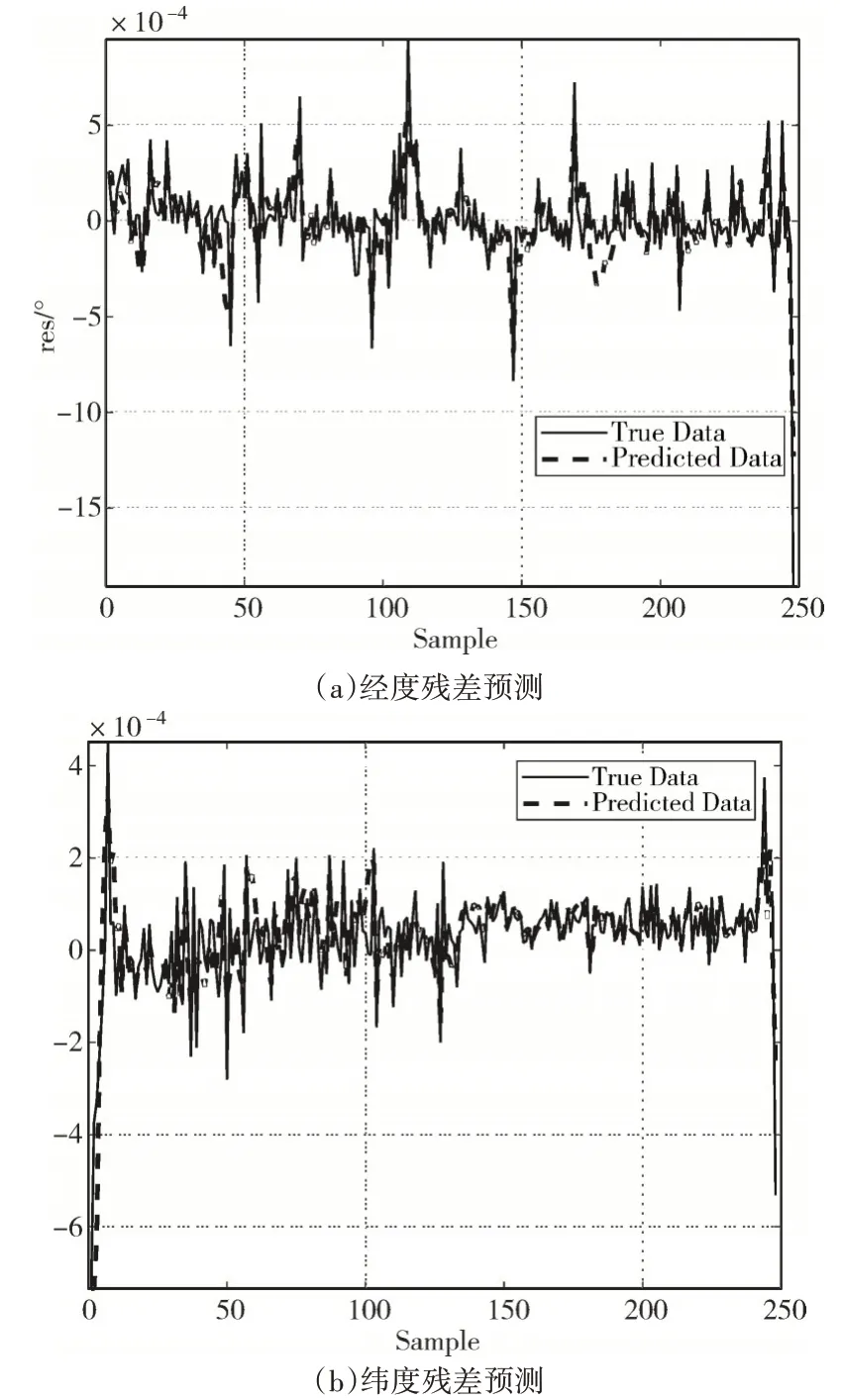
圖5 軌跡2殘差預測

4.6 實驗結果及分析

為了更好地說明LSTM-EMD 模型在船舶運動軌跡預測中的優越性，同時給出基于傳統的BP 神經網絡模型和單一LSTM 模型的軌跡預測結果及誤差。兩組數據的預測結果分別如圖6～圖7所示。

圖6 軌跡1預測結果

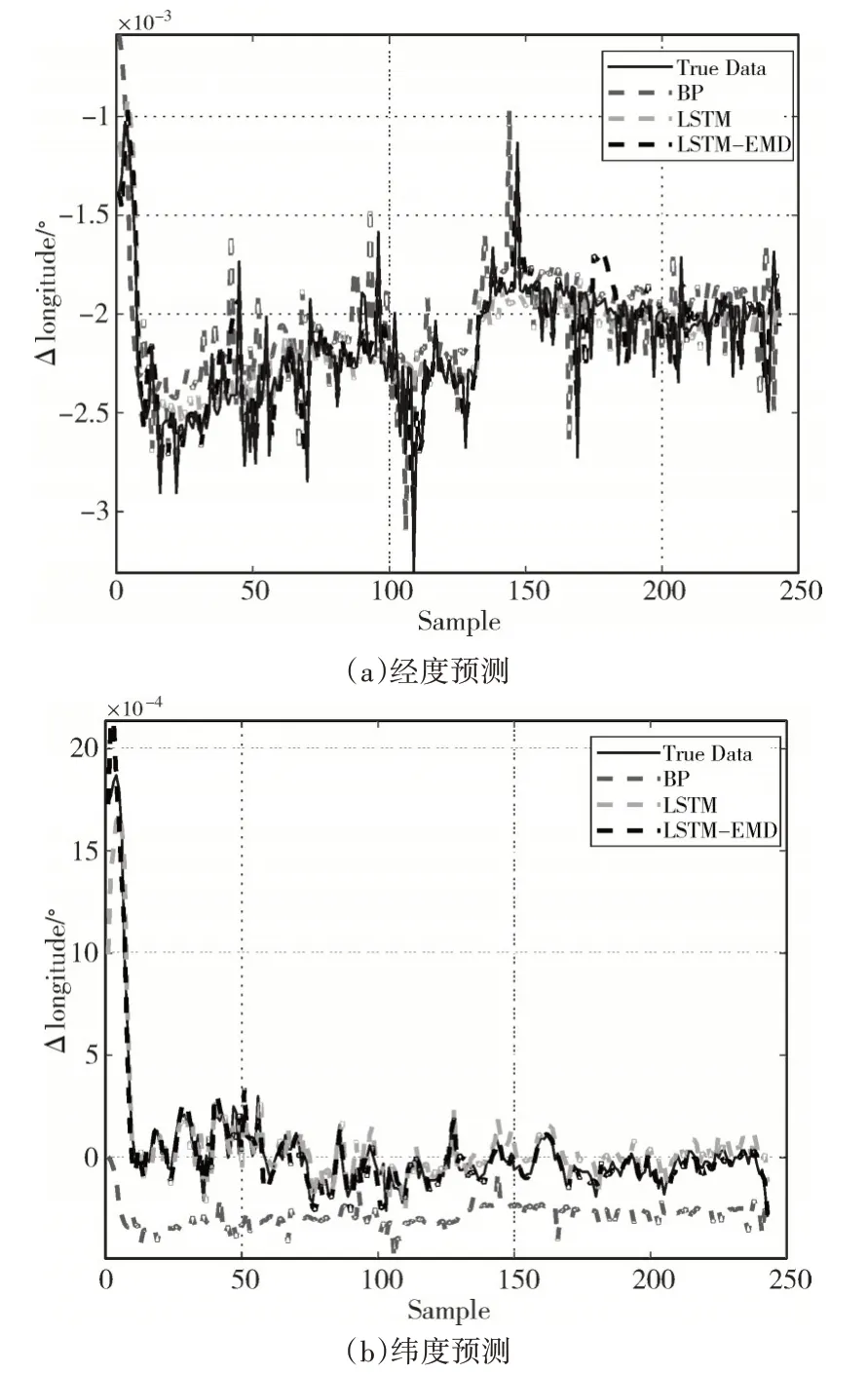
圖7 軌跡2預測結果

通過圖6～圖7可以看到，三種模型在整體上都能較地好預測船舶運動軌跡。但BP神經網絡模型表現較差，預測效果不及LSTM 模型和LSTM-EMD模型；LSTM 模型比BP 模型穩定，在經度預測和緯度預測都有不錯的效果；LSTM-EMD 模型表現最好，能夠較為準確地預測經度和緯度。下面給出更加直觀的模型誤差曲線，如圖8～圖9所示。并利用評價指標對預測結果進行統計分析，如表1、表2所示。

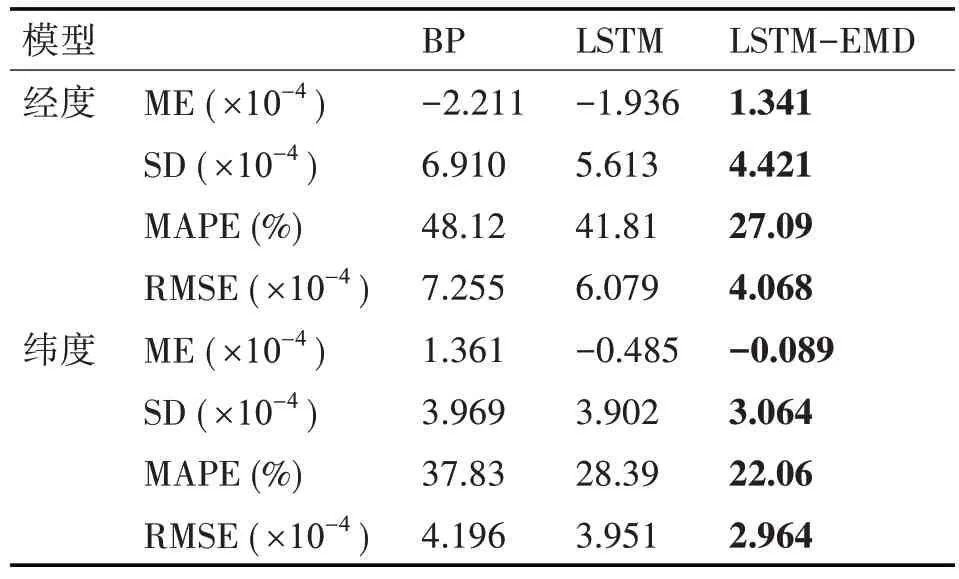
表1 軌跡1的Mean Error、SD、MAPE和RMSE

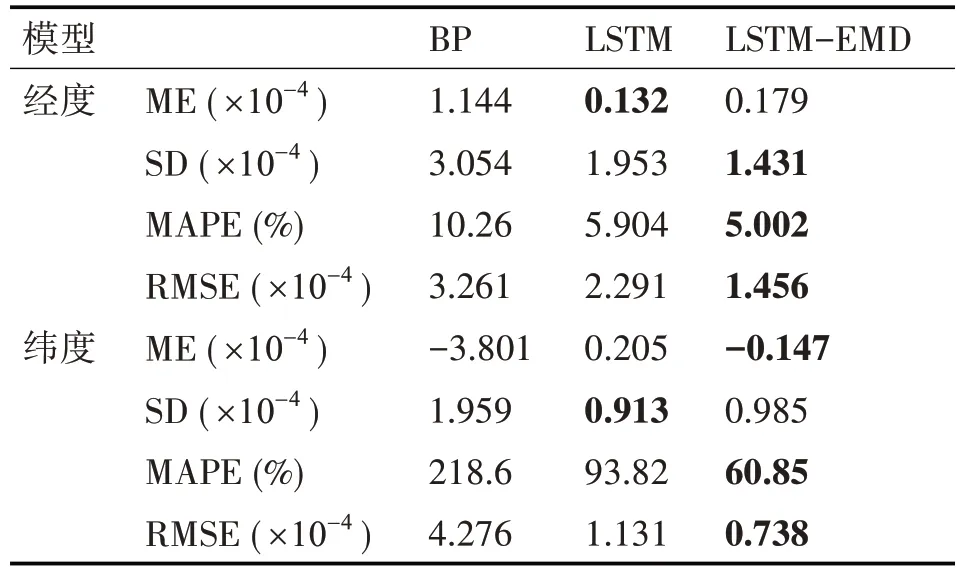
表2 軌跡2的Mean Error、SD、MAPE和RMSE

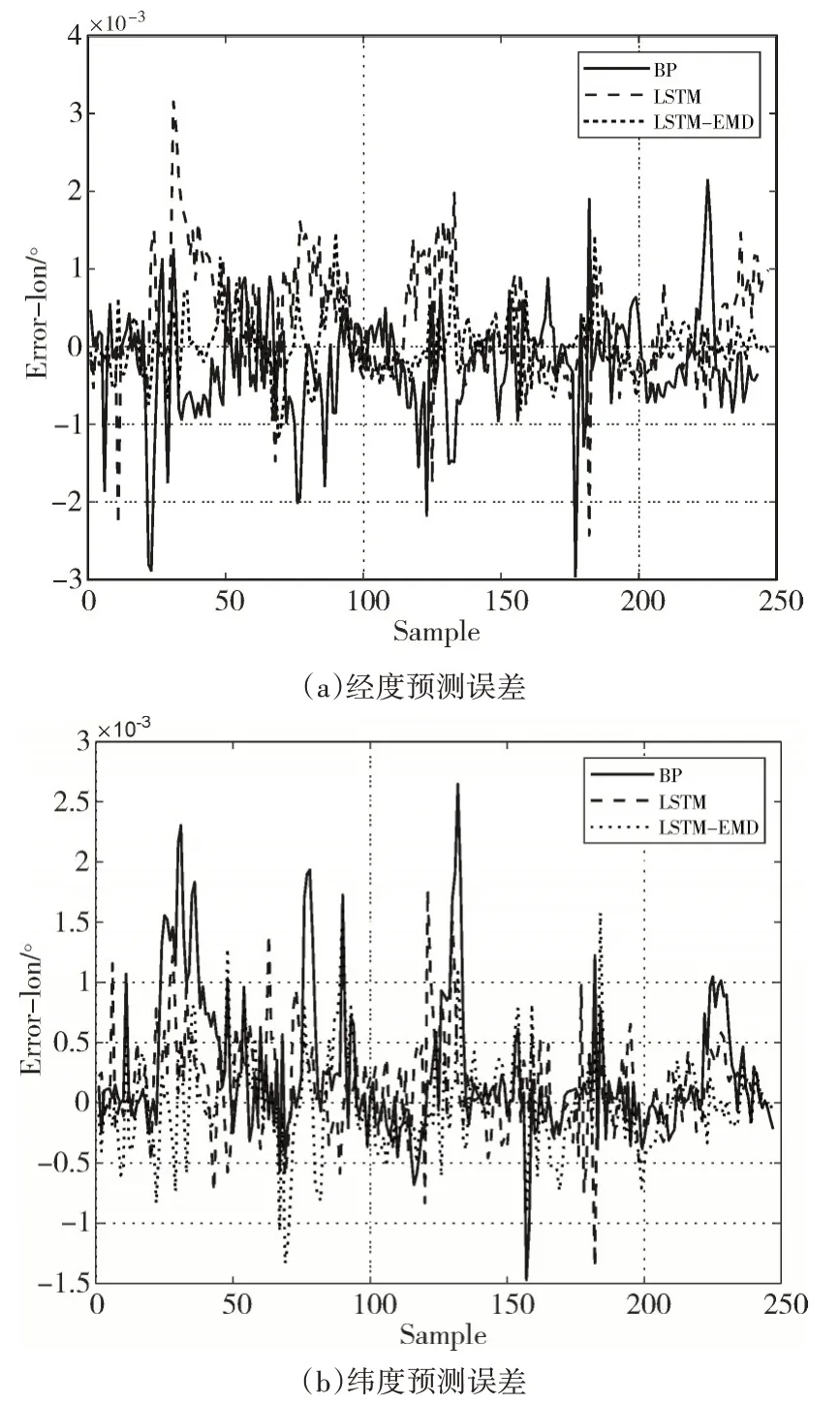
圖8 軌跡1預測誤差

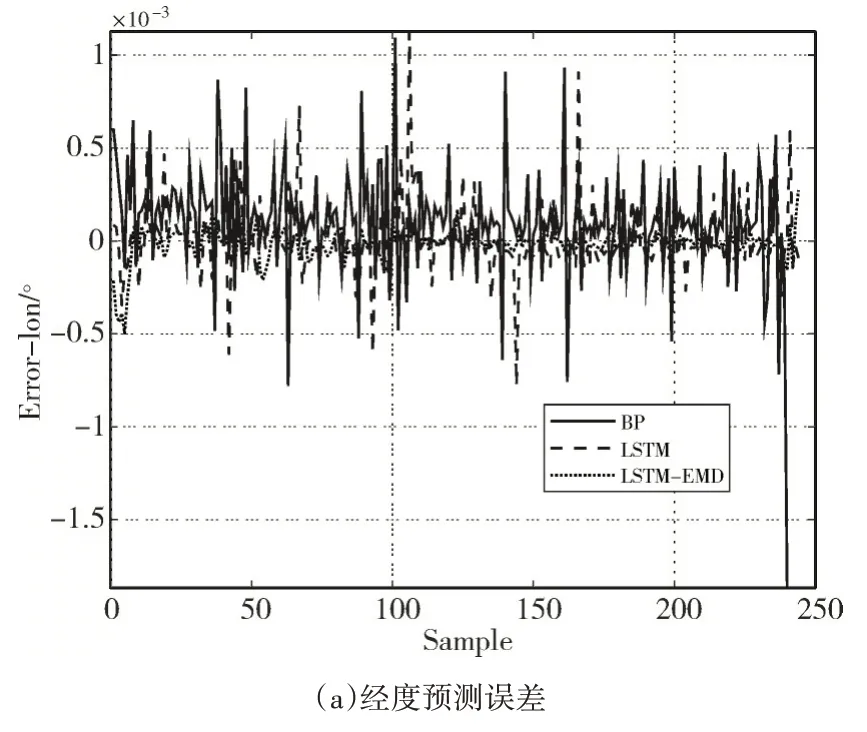
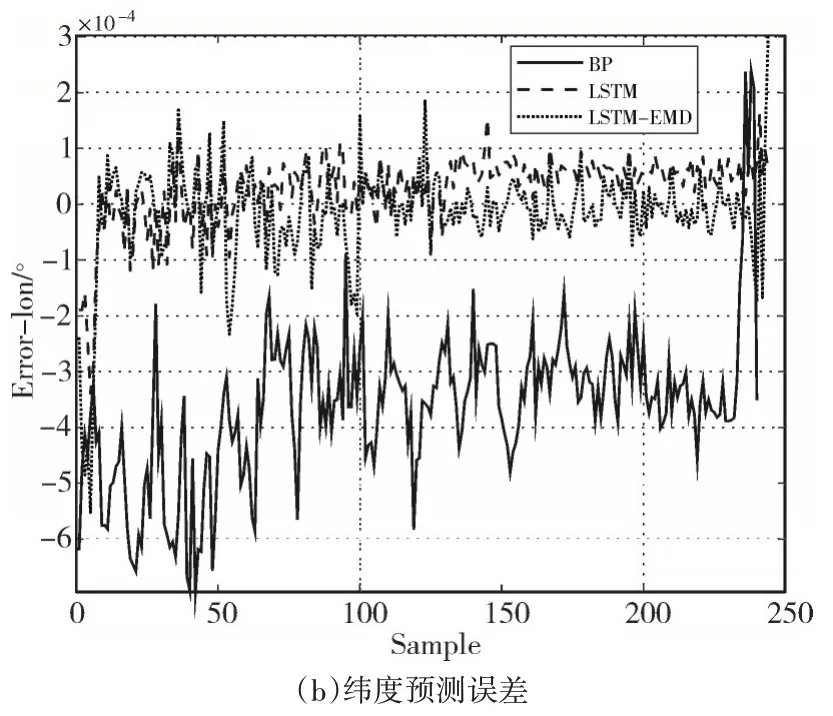
圖9 軌跡2預測誤差

通過分析圖6～圖9 以及表1、表2 可得，三種模型對船舶運動軌跡的預測都有良好的效果，其中LSTM-EMD 模型的表現最好。選取表1 的數據進行具體分析，根據表1 的數據，在經度預測中，LSTM-EMD 模型相對于BP 模型和LSTM 模型，預測結果的平均絕對百分比誤差分別降低了21.03%和14.72%，效果分別提升了43.93%和33.08%；在緯度預測中，預測結果的平均絕對百分比誤差分別降低了15.77%和6.33%，效果分別提升了29.36%和24.98%。且經度預測和緯度預測的結果都體現出，LSTM-EMD 模型的標準偏差SD 比BP 模型和LSTM 模型更接近平均誤差，表明LSTM-EMD 模型的船舶軌跡預測不僅有較高的預測精度，還能保證大多數預測位置與實際位置偏離程度更小。表2的數據同樣支持上述結論。

5 結語

AIS 對于保障航海安全具有重要作用，也為船舶軌跡預測提供了研究基礎，本文基于AIS 數據，針對船舶軌跡的單步預測提出一種LSTM 神經網絡和EMD 分解算法相結合的預測模型，該模型首先利用LSTM 模型對原始數據建模并進行初始預測，預測結果利用EMD 算法進行分解，再對各IMF分量進行預測，最后將殘差預測值進行補償得到最終的預測結果。實驗部分包括數據預處理、LSTM模型預測、EMD 分解、殘差預測及補償四個步驟，并利用三條時間長、數量多的AIS 軌跡數據進行實驗驗證，將LSTM-EMD 模型的實驗結果與BP、LSTM 模型的預測結果作對比，其結果表明：LSTM-EMD 模型對于船舶運動軌跡的預測有著更好的效果，對于提高航海安全性有一定的積極作用。