對空觀察哨雙站測向交叉定位誤差分析與驗證?

孟圣波 李鵬飛 黃建廷

（陸軍炮兵防空兵學院 鄭州 450000）

1 引言

現代防空戰場，由于對空偵察雷達受目標散射特征、地物雜波、氣象條件、地球曲率以及地形地物遮蔽等因素的影響，對高度100m 以下的超低空目標很難進行有效探測和穩定跟蹤。通過對近些年從陸空對抗演習中獲取的數據分析來看，演習中一旦藍軍戰機進入攻擊陣位并采取超低空突防戰術時，對空偵察雷達的平均有效預警時間比不足20%［1］。低空預警的能力不足很容易造成火力單元的準備時間不足，給防空戰斗帶來很大被動，甚至導致整個防空戰斗的失敗。當前，對空偵察雷達網對超低空突防飛機發現難的問題已成為制約防空兵作戰效能發揮的瓶頸。因此，拓展新手段進行超低空目標探測是當前防空兵發展的迫切需要。

回顧我軍防空作戰的歷史，對空觀察哨憑借自身機動靈活、抗干擾性強、可前伸布置等優勢，在對超低空目標的偵察中始終發揮著積極作用。若觀察哨攜帶具有高精度測角功能的光學偵察器材組成雙觀測站，通過交叉定位的方法可實現對超低空目標的定位跟蹤。但由于偵察器材存在測角誤差，導致雙站交叉定位結果也會存在誤差，而且該誤差范圍受雙站基線長度、目標與觀察哨相對位置關系等諸多因素的影響而變化。若不能正確把握定位誤差的變化規律，雙站布設不合理時就很難獲取符合軍事需要的空情信息。目前，對雙站測向交叉定位基本原理研究的成果較多，但對其誤差變化規律的分析較少，不足以支撐對空觀察哨在實戰中的運用。因此，本文基于雙站測向交叉定位的原理研究不同布站方式下定位誤差的變化規律，總結出更為合理的布站方案，為提升對空觀察哨在實戰中的應用質效提供支撐。

2 對空觀察哨雙站交叉定位的模型

2.1 理想的雙站交叉定位模型

雙站交叉定位即利用兩個高精度測向裝備在不同的位置對目標進行測向，而后將所得測向數據和兩站間的基線距離通過三角運算處理，確定目標的空間位置。將此問題放在坐標系中研究，其相對位置關系可用圖1所示。

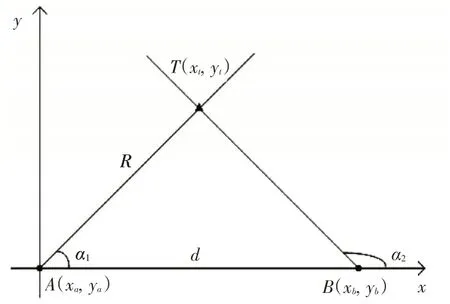
圖1 雙站交叉定位相對位置關系

為方便進一步分析，假定主站A 位置為原點，主站A 至輔站B 的方向為x 軸的正方向，則A 站坐標（0，0），B 站坐標（xb,yb），目標T 坐標(xt,yt)。兩觀察哨間距離為d，所測目標仰角分別為α1、α2則可計算目標距離主站A的距離為

根據圖1可得以下聯立方程組：

求解可得

從以上過程可以看出，只要知道兩觀察哨的位置及所測目標仰角α1、α2，就可以計算出目標T 的坐標位置(xt,yt)及其與主站間的距離R。

2.2 實際應用中的雙站交叉定位模型

在實際應用中，由于光學偵察器材自身存在測角誤差，兩站所測目標的仰角α1、α2也必定會存在一定的差值。當使用相同的設備進行雙站交叉定位時，其測角誤差均為θ，便會形成如圖2中EFGH所示的定位模糊區。若定位誤差過大則難以將觀察哨空情和雷達空情進行關聯，也就無法滿足空情融合的需要。因此只有定位誤差符合一定精度要求時觀測到的空情信息才有效，所對應的布站方案才可行。于是本文以最大誤差距離Dismax≤50m為符合定位要求的限定條件展開研究。

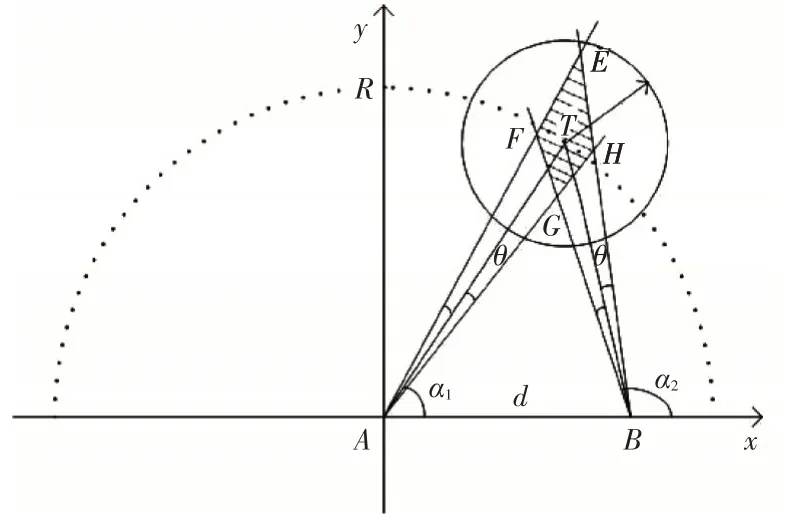
圖2 有誤差情況下雙站交叉定位模型

根據上述模型，可以求得T、E、F、G、H 各點坐標：

由此可計算出最大誤差距離Dismax：

3 實驗及結果分析

3.1 仿真實驗

3.1.1 仿真流程

式（9）為最大誤差距離的計算方法，為了研究其在不同布站方式下的變化規律，本文利用Matlab軟件進行仿真分析。假設觀察哨最大探測距離為R，令主站A 固定于坐標原點，輔站B 可沿x 軸方向移動，主輔站之間的基線距離為d。本仿真實驗主要研究當目標在距離主站為R 的圓上做如圖2 中虛線所示得圓周運動時，兩站對目標實施交叉定位的精度受基線距離d 和主站仰角α1兩個變量的影響情況。通過對比分析得出在主站探測距離不變時，不同基線距離下，交叉定位最大誤差距離的變化情況。

設R=8km，A、B 兩站所測目標仰角α1、α2的取值范圍均為（0，180°），光學偵察設備的測角誤差θ為1 密位（0.06°）。為了對定位誤差進行充分對比，取基線距離與探測距離滿足(dR)三種關系的多組數據進行仿真，本文重點分析了基線距離d 依次取4km、6km、8km、10km、11.3km、15km 的6 種布站方式下的定位誤差情況。根據以往的研究結果，當目標與兩觀察點距離相等且為等腰直角三角形時交叉定位的模糊面積最小，由此認為，時可能具有較高的定位精度，故添加了基線距離這一數據進行對比，確定的仿真流程如圖3所示。

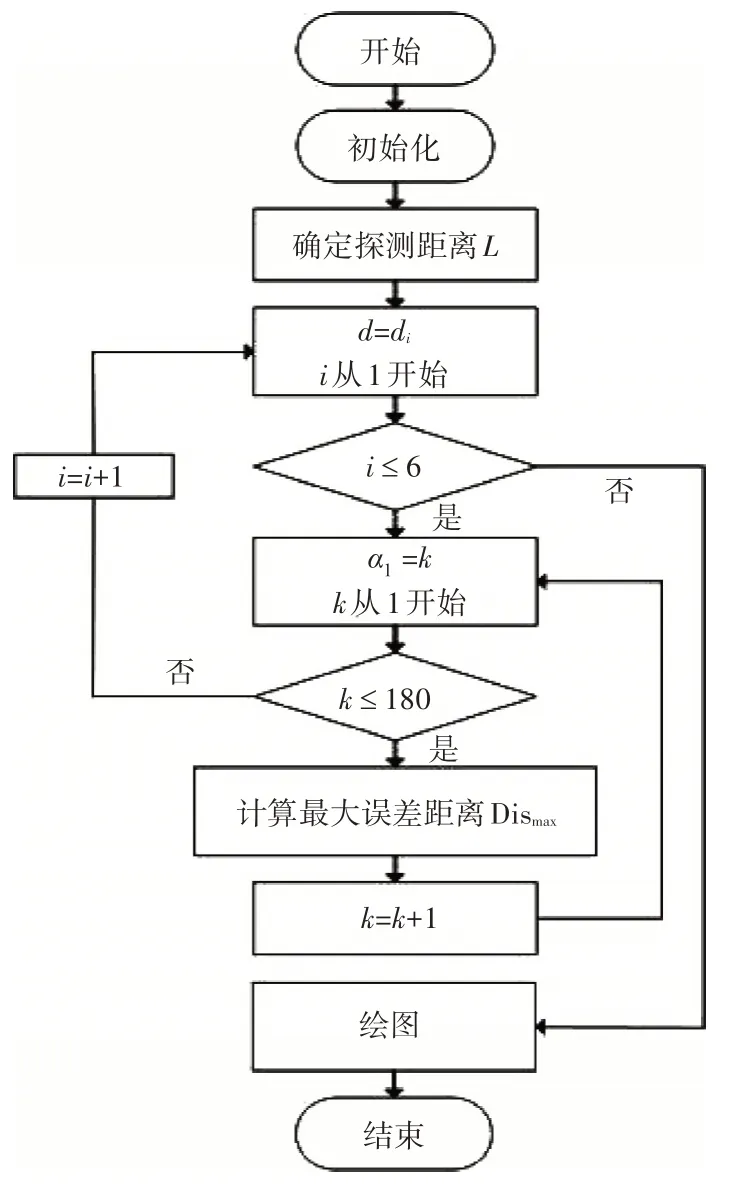
圖3 仿真流程圖

3.1.2 仿真結果分析

本文將符合定位要求的主站所測目標仰角α1的取值稱為主站有效觀測區間，若有效觀測越廣，說明對應的布站方案越合理。對7 種不同布站方式下的數據進行梳理匯總后，得出圖4 所示的定位最大誤差距離與主站測量仰角對應關系圖，表1 則是不同布站方式下主站有效觀測區間匯總表。

表1 主站有效觀測區間統計表

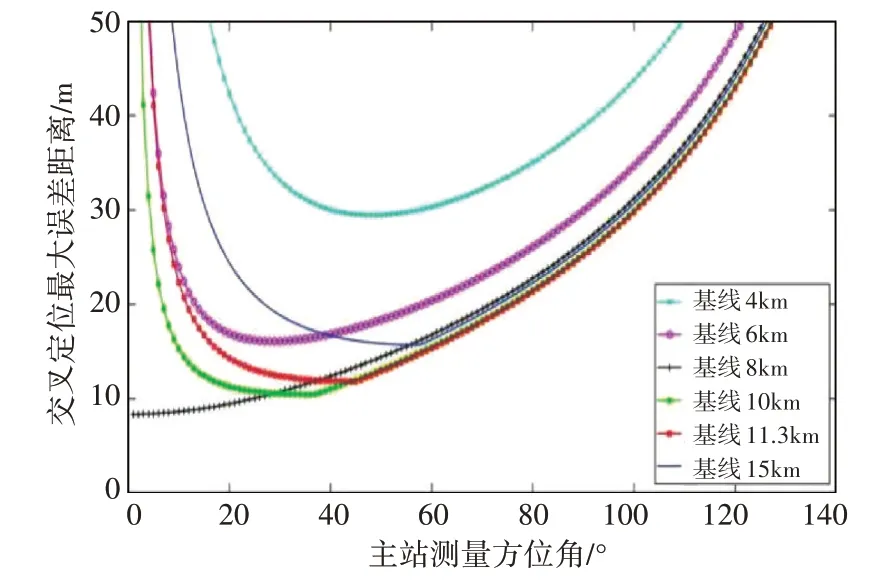
圖4 探測距離為8km時的仿真結果

分析圖4 和表1 可知，在0°<α1≤28°情況下，d=R=8km 時定位誤差最小；29°≤α1≤44° 情況下，d=10km 時定位誤差最小；45°≤α1≤127°情況下，d=R≈11.3km 定位誤差最小。匯總以上數據發現，符合定位誤差最小條件的基線距離與探測距離一直滿足R≤d≤R，且在此條件下主站有效觀測區間都比較廣。因此，基線距離與探測距離滿足R≤d≤R關系時的布站方案最合理。

為了驗證以上結論的準確性，利用此方法繼續對探測距離為5km、3km 兩種情況進行仿真和分析，得出圖5、表2所示結果。

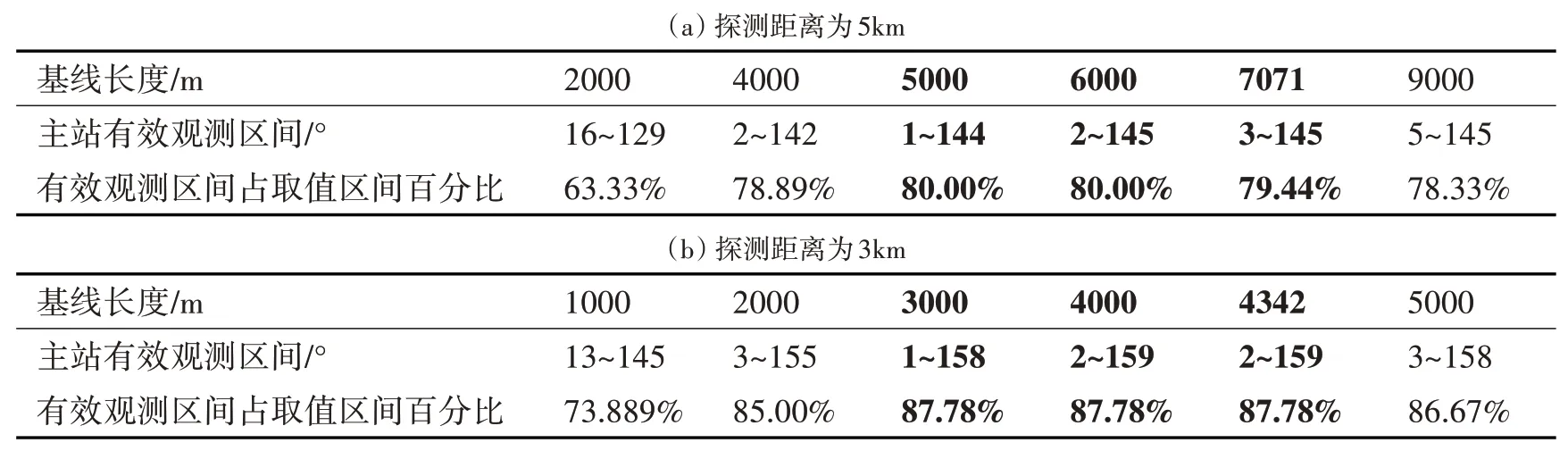
表2 主站有效觀測區間統計表

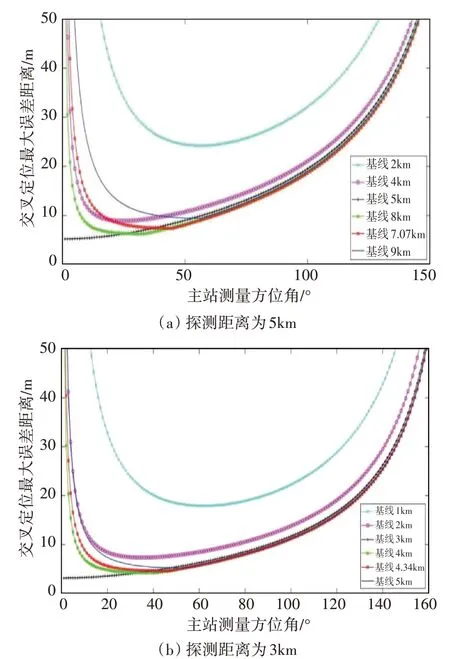
圖5 仿真結果圖

綜合圖5、表2得出以下結論：對空觀察哨使用高精度光學偵察器材進行雙站交叉定位可以獲得有效空情，且在合理布站的情況下能較大程度降低定位誤差。布站基線距離與探測距離滿足R≤d≤R關系時所對應的布站方式定位精度高、主站有效觀測區間廣，此范圍為最優布站基線距離范圍。

3.2 實測實驗

為了進一步驗證研究結論的準確性，本文開展了利用觀察哨組網超低空偵察監視系統對無人機進行雙站交叉定位的實裝驗證，分別在3 種不同基線距離對無人機航跡上的5 個不同測量點進行定位，實驗過程如圖6所示。

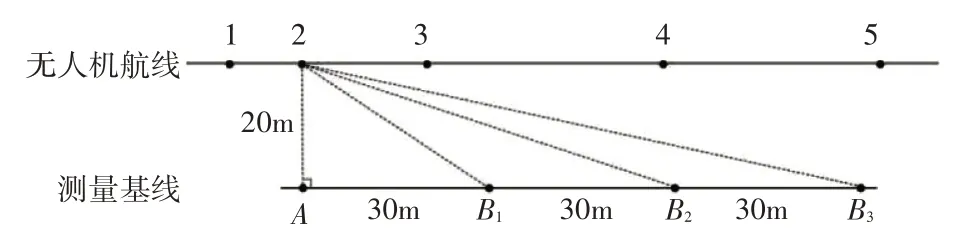
圖6 實驗示意圖

3.2.1 實驗步驟

實驗中，將觀察哨1站固定部署在A點，觀察哨2 在距離A 點正東方向30m、60m、90m 處的三個觀測點B1、B2、B3部署，雙站對無人機航線上的5 個測量點進行交叉定位。無人機在與測量基線平行且相距20m的航路上由東向西飛，經過每一個測量點時在空中懸停，此時1 站位于A 處，2 站分別在B1、B2、B3處與A 站同時對無人機觀測，待三個觀測點全部完成定位和記錄工作后，無人機再飛行至下一測量點，1、2 站再按照上述步驟實施測量，記錄數據如表3所示。

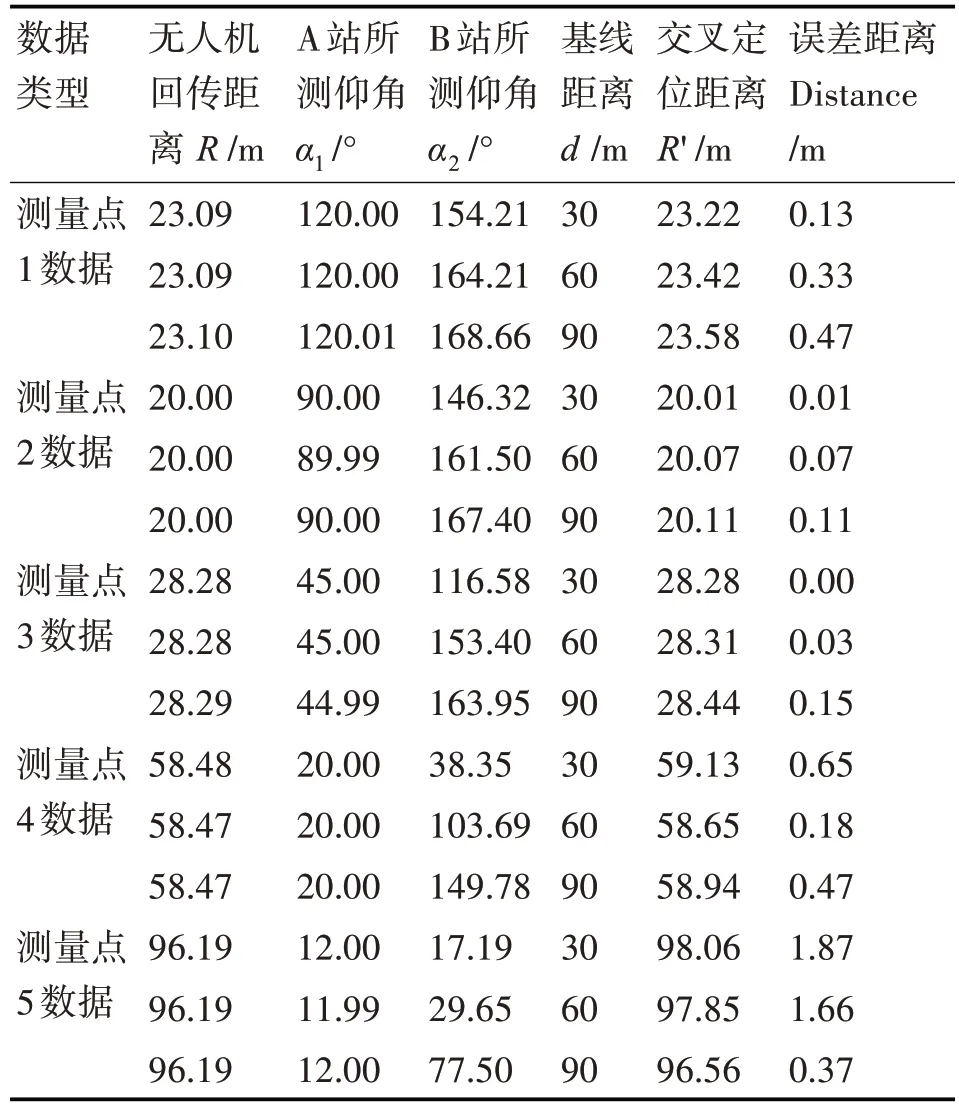
表3 實驗測量及計算結果

3.2.2 實驗結果及分析

分析以上實驗結果，在測量點2 的三組數據中，基線距離與探測距離均滿足d> 2R的關系，此時d 越接近 2R時誤差距離越小；測量點5 的三組數據中，基線距離與探測距離均滿足d

4 結語

本文通過理論分析與實驗相結合的方式對雙站測向交叉定位誤差的變化規律進行了深入分析，著重研究了不同布站方案對定位精度的影響，并得出了優化布站基線長度范圍，為光學觀察哨優化部署提供了數據支撐，有效提升對空觀察哨上報空情質量，為其在實戰中的應用提供幫助。但雙站交叉定位在觀測角度上仍有一定的局限性，若運用更多的觀察哨組網構成一種分布式多傳感器的廣域監測系統，可以在更大區域內實現對目標更精準的定位，其優化布站理論有待進一步研究。