插電式混合動力汽車加速度預測及能量管理

王超，薛斌強

（青島大學自動化學院，山東青島 266071）

為緩解能源和環境壓力，新能源汽車成為汽車產業的重點方向[1]。PHEV 具有排放量低、行駛里程長等優點，是新能源汽車的研究熱點[2]。其中，PHEV的能量管理策略是決定混合動力汽車燃油經濟性的關鍵技術[3-4]，其主要有基于規則的能量管理策略[5]和基于優化的能量管理策略[6-7]兩類。基于規則的控制策略簡單實用、控制成本低，在實際車輛中應用廣泛，但是此策略的控制規則通常通過工程經驗制定，優化效果和適應性較差[8]。基于優化的能量管理策略包括瞬時優化和全局優化。以等效油耗最小策略為代表的瞬時優化能量管理策略執行效率高，但是無法保障全局最優，且等效因子的最優取值問題難以確定[9]；基于全局優化的能量管理策略可以實現理論上的最優控制，但全局優化算法程序復雜、運算量大，難以實現實時控制[10]。除此之外，電池精確建模也是混合動力汽車能量管理中的關鍵部分，為了將電池的電流和電壓與動力系統其余部件的功率相關聯，通常使用電池等效電路模型[11]。基于充放電試驗數據建立Rint 等效電路模型[12]簡單直觀，計算量小，但精度較低。文獻[13-14]采用一階等效電路建立電池模型，相比于Rint 等效電路模型考慮了電壓的動態特性，精度更高且模型參數容易辨識。

針對上述問題，設計一種基于隨機模型預測控制的PHEV 能量管理策略。選擇加速度為預測量，采用馬爾可夫鏈模型進行預測，根據車輛縱向動力學模型和預測的加速度信息求解預測時域內的需求轉矩。根據全局優化結果制定理論電池荷電狀態（State Of Charge，SOC）參考曲線，添加關于SOC 的代價函數，防止SOC 快速下降。選擇DP 求解預測時域內的最優轉矩分配，確定SOC 可達區域并在此區域內離散SOC，減少計算量。

1 動力系統模型

1.1 整車縱向動力學模型

針對具有并聯結構的PHEV 展開研究，分析其動力學模型。PHEV 有發動機和電機兩個動力源，也有連接外部電網的接口。發動機和電機通過齒輪等結構將轉矩耦合后輸入到主減速器再傳遞到車輪，提供車輛行駛過程中的總需求轉矩。其系統結構圖如圖1 所示。

圖1 插電式并聯混合動力汽車結構簡圖

通過對整車能量分析，PHEV 的縱向動力學模型為：

其 中Tr為需求轉矩；ηT為傳動效率；i0為主減速器速比；rw為車輪半徑；Cd為空氣阻力系數；Af為迎風面積；v為車速；m為整車質量；g為重力加速度；f為滾動阻力系數；θ為坡度角；δ為旋轉質量換算系數。

1.2 動力電池模型

電池作為電化學能量儲存系統是混合動力汽車的關鍵部件，因此電池建模是影響混合動力汽車能量管理的重要因素。混合動力汽車中動力電池為多個單體電池串聯或多個模組并聯組成的電池組。電池組的一階RC 等效電路[15]如圖2 所示。串聯電阻R0為歐姆內阻，表示由于電線和電極間的實際電阻以及降低終端可用凈功率的耗散現象產生的歐姆損耗；電阻Rp和電容Cp分別為極化內阻和極化電容，兩者組成的RC 回路用于模擬電池的動態響應。

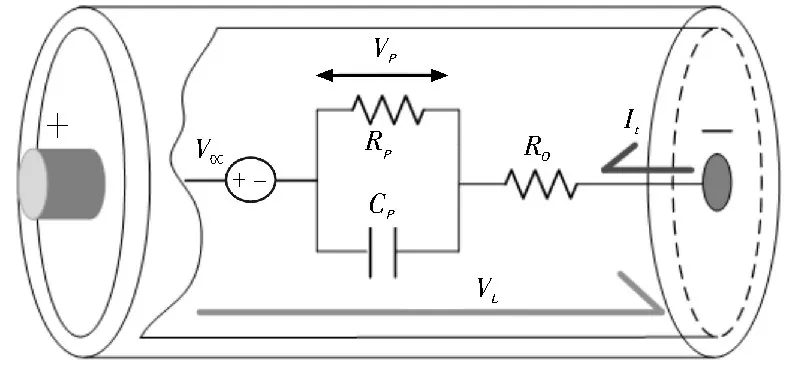
圖2 一階RC等效電路模型

通過基爾霍夫定律和歐姆定律，可得：

式中，VP為RC回路上的電壓；VL為負載電壓；Voc為開路電壓；Δt為采樣時間；I為電池輸出電流。為了提高論文可讀性，在后續的公式中用A表示exp(-Δt/CpRp)。

根據公式（2），電流的顯式表達式為：

式中，Tm為電機轉矩；ωm為電機轉速；ηm為電機效率。

假設所有電池單體的特性相同，整個組件的參數可由電池單體的參數進行計算：

Ns是模組中串聯的單體電池數；Np是并聯的模組數；Voc,cell、R0,cell、Rp,cell和Cp,cell分別為組成電池組的單體電池的開路電壓、歐姆內阻和RC回路上的電阻和電容。

通過恒流放電測試和混合脈沖功率特性（HPPC）測試，分析電池的電壓響應并記錄數據。通過最小二乘法對記錄的數據進行擬合，獲得Voc,cell，R0,cell，Rp,cell和Cp,cell與SOC 之間的非線性關系：

式（5）-（6）中，bi、ci、di、ei和f1為多項式擬合系數。

結合式（3）-（6），電池組的荷電狀態SOC 表示為：

式中，SOC0為電池組的SOC 初始值；Qb為電池組容量。

2 隨機模型預測控制

基于模型預測控制的能量管理策略是基于預測的未來工況將全局最優問題轉化為預測時域內的局部最優問題，通過滾動優化不斷更新預測時域內的優化問題，使優化結果接近全局最優。

2.1 馬爾可夫加速度預測模型

為了實現PHEV 的最優轉矩分配，需要準確地預測出車輛未來的行駛狀態。由于車輛未來狀態僅取決于當前狀態，具有較強的隨機性和無后效性[16]，因此，采用馬爾科夫鏈模型對加速度進行預測，其中馬爾科夫鏈建立步驟如下：

采用近鄰法將加速度a離散為p個狀態，Pi,j表示k時刻加速度為ai條件下，k+1 時刻加速度為aj的轉移概率，Pi,j為概率轉移矩陣的第i行第j列元素，可通過最大似然估計法計算，Mi,j為加速度從ai轉移到aj的次數，Mi為加速度從ai轉移的次數。

2.2 隨機模型預測控制的建立及求解

通過上述的馬爾可夫模型以及當前的車輛行駛狀態能夠預測出車輛在預測時域內的加速度信息，并結合車輛縱向動力學模型計算得到預測時域內的需求轉矩。這樣預測時域內的能量管理問題可以描述為以動力電池荷電狀態SOC 為狀態變量，驅動電機轉矩Tm為控制變量，燃油消耗量最小為優化目標的模型預測控制優化問題。

優化過程中，系統當前時刻的狀態量由前一時刻的狀態量和控制量確定，在每一次決策之后都會引起狀態轉移，狀態轉移方程為：

把預測時域內PHEV 的油耗作為優化目標，則在k時刻給出混合動力汽車能量管理系統的預測控制性能指標：

式中，Jk為預測時域k～k+p內總的燃油消耗量；L為預測時域內每個時刻的瞬時油耗；Te為發動機轉矩；ne為發動機轉速；be為發動機燃油消耗率；h為關于SOC 的二次代價函數；SOCr為預測時域內每一時刻的SOC 參考值；α為正的權重系數。

由于客觀因素限制，電池SOC、電機轉矩、電機轉速、發動機轉矩、發動機轉速所受約束為：

由上述預測模型（9）、目標函數（10）和約束條件（11）組成的模型預測控制優化問題可采用動態規劃進行求解。為了降低采用DP 求解的計算量，根據當前時刻的電池SOC 和控制量可能的取值確定SOC的可達范圍，在此范圍內對控制變量和狀態變量進行離散化，利用Bellman 最優化原理在預測時域內逆向逐步求解最優控制律:

3 仿真驗證及結果分析

仿真驗證時選用的PHEV 主要參數為:整車質量為1 570 kg，滾動阻力系數為0.014，車輪半徑為0.29 m，空氣阻力系數為0.35，迎風面積為2.2 m2,主減速器速比為4.88，傳動系數為0.92，發動機峰值轉矩為130 N·m，電機峰值轉矩為120 N·m，電池容量為30 A·h，額定電壓為346 V。選取城市道路循環（Urban Dynamometer Driving Schedule,UDDS）工況作為樣本工況并提取車速和加速度數據，采樣步長取1 s，速度離散間隔取10 km/h，加速度離散間隔取0.3 m/s2，由式（8）可得不同車速對應的加速度轉移概率矩陣。為驗證基于模型預測控制的能量管理策略的有效性，在Matlab/Simulink 中進行仿真驗證。

循環工況及PHEV 在5 倍工況下的電機、發動機轉矩如圖3 所示。PHEV 能夠通過外部充電補充電池的電量消耗，且在電池SOC 約束范圍內SOC 值對車輛動力性能無影響，為了充分利用電池電能采取電量消耗模式，使電池SOC 在循環工況結束時達到允許的最小值。選取預測時域為15 s，采樣時間間隔為1 s，SOC 初始值為0.7，終值為0.5。圖4 為基于MPC 的能量管理策略車輛工作模式柱狀圖和發動機工作點分布圖。從圖中可以看出電機的放電狀態多于充電狀態，且充電狀態大多處于制動能量回收模式，電池電量得到了充分利用。發動機主要在轉矩需求較大的加速階段被啟動，且發動機總體運行在高經濟性區域。

圖3 UDDS循環工況及電機、發動機轉矩

圖4 工作模式時間占比及工作點分布

RC-MPC 策略與DP 能量管理策略、基于規則的能量管理策略和傳統MPC 能量管理策略的電池SOC變化對比圖和燃油消耗對比圖如圖5 所示。SOC 初始值為0.7，到達行程終點時各控制策略對應的SOC值分別為0.506 0、0.507 3、0.508 7、0.5220。忽略SOC變化量差異，在電池SOC 消耗模式，5 倍UDDS 路況的情況下，在RC-MPC 策略下車輛油耗為595.27 g，基于DP 的能量管理策略車輛油耗為575.77 g，基于規則的能量管理策略車輛油耗為768.39 g，傳統的MPC 能量管理策略車輛油耗為666.40 g。該文提出的能量管理策略燃油經濟性與基于DP 的策略效果接近，但是基于DP 的策略得到的是理想的優化結果，實際上無法實現，與基于規則的能量管理策略相比油耗降低22.53%，與傳統的MPC 能量管理策略相比油耗降低13.64%。

圖5 各策略SOC曲線圖及油耗曲線圖

4 結論

通過基于DP 的模型預測控制策略，實現了對PHEV 轉矩分配的有效控制。首先建立了PHEV 的能量消耗計算數學模型和電池組的一階等效電路模型。其次將加速度的動態過程描述為隨機馬爾可夫過程，并根據UDDS 路況樣本數據建立了加速度預測模型來預測加速度。然后基于理論參考軌跡，設計基于預測控制的PHEV 能量管理策略，并采用DP方法進行優化求解。最后仿真驗證表明，車輛能夠充分利用電能，使得發動機主要工作在高經濟性區域內，與基于規則的控制策略相比具有更高的燃油經濟性。該方法能夠在PHEV 的能量管理中起到良好的效果。