基于RFE 特征選擇的PSO-SVM 用電量預測算法

羅紅郊，馬曉琴，孫 妍，張華銘

（1.國網青海省電力公司信息通信公司，青海西寧 810000；2.北京清軟創新科技股份有限公司，北京 100085）

近年來，隨著新型電力系統建設進程的加快，電力行業也開始逐步推進企業數字化轉型。其中，計算機技術是賦能企業數字化轉型的重要途徑。在電力市場化改革背景下，新能源將逐漸占據主體地位。相較于傳統的火力發電，在新能源接入后電力供給側的波動性與隨機性將顯著提升，這便要求更準確地對負荷大小進行預測，從而把控用電量趨勢[1-3]。

隨著機器學習技術的發展，神經網絡(Artificial Neural Network,ANN)、支持向量機(Support Vector Machine,SVM)、多元回歸(Multiple Regression Analysis,MRA)等多個數學模型已逐步應用于電力系統的用電量預測中。但此類算法自身的訓練及求解過程仍存在迭代效率低、容易陷入局部最優等問題，會直接影響到模型的預測精度[4-5]。此外，由于影響用電量的因素較多，在進行模型算法的特征選擇時無法全面顧及，這導致模型在訓練時易產生維度缺陷，從而影響算法的性能發揮[6-7]。基于上述分析，該文一方面從影響用電量的因素出發，使用遞歸特征消除法(Recursive Feature Elimination,RFE)篩選用電量特征指標，以提高機器學習算法的迭代效率；另一方面則對傳統支持向量機算法的訓練方式加以優化，引入改進后的粒子群(Particle Swarm Optimization,PSO)算法來提升模型的預測精度。

1 理論分析

1.1 算法框架

支持向量機(SVM)是一種常見的基于統計學理論的機器學習算法，其在小樣本、高維度的非線性擬合問題上具有廣泛的應用[8-13]。但傳統的SVM 算法在確定回歸參數時，通常基于計算機遍歷、人工選取等方法，從而影響了算法的使用效率及預測性能，因此需對其進行優化與改進[14]。設規模為l的樣本集為{(xi,yi),i=1,2,…,l}，xi、yi分別是輸入值與其對應的輸出值。設f(x)為以x為自變量的回歸估計函數：

式中，ε是不敏感損失函數。當樣本落入以f(x)為中心且距離為2ε的區域時，記回歸損失為0；而當樣本未落入該區域時，則模型對樣本進行懲罰。SVM 算法通過構造合適的f(x)，在ε盡可能較小的情況下，實現最少的樣本懲罰L。以線性的f(x)為例，可表示為：

此時，上述的優化問題可轉化為：

通常在求解時，為提升模型的泛化性能，會引入松弛變量ξi、與懲罰系數C，此時式（3）可改寫為：

在求解式（4）時，引入拉格朗日乘子(Lagrange Multiplier)，此時根據：

1.2 基于PSO的算法優化

根據上文所描述的基于傳統優化方式SVM 算法中，C、ε等參數均會影響模型回歸的精度。因此，文中使用粒子群(PSO)算法來確定SVM 算法的參數[15-16]。該文粒子群算法中引入了自適應調整機制和慣性權重機制，具體流程如圖1 所示。

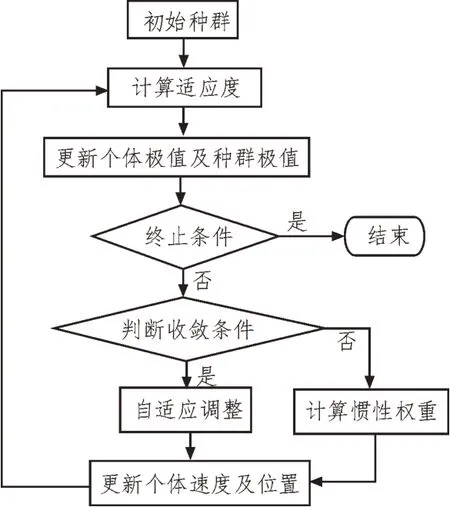
圖1 基于PSO優化的SVM算法流程

首先對于規模為m的種群，按照20%、30%、50%的比率劃分為A、B、C 三個子種群：

1）在A 種群內部，變異策略為：

慣性權重的計算策略為：

2）在B 種群內部，變異策略為：

慣性權重的計算策略為：

3）在C 種群內部，變異策略為：

慣性權重的計算策略為：

2 方法實現

2.1 基于RFE的特征選擇策略

該文算法所設計的應用場景主要用于居民用電量預測。經過前期的數據清洗，已獲取某地區2017—2021年間342個小區每日的用電量數據，且數據采集的頻率為15 min/次。此外，還搜集并清洗了小區用戶規模、小區地理位置、臺區容量以及居民負荷等標號為1-30 的不同類別數據，作為模型的輸入特征。

根據SVM 算法的特性，該模型對于低維數據的回歸具有更優的泛化性能。因此，需從30 組特征中隨機選取一個作為PSO-SVM 模型的輸入。

該文在進行特征選擇時，基于SVM 的遞歸特征消除特性(RFE)基本思路描述如下：對于目標函數Lp，計算在1-30 個特征中的第i個特征Δwi被剔除時Lp的變化情況，即：

此時，能夠得到樣本集中每個特征的排序系數：

將采集的所有數據進行標準化處理，消除數據量綱對模型預測的影響。

根據圖2 的計算結果可知，使用11 個指標作為模型的特征輸入時，即可對模型精度產生97.99%的貢獻度，且PSO-SVM 能夠取得綜合最優的性能。這11 個指標及各自的貢獻度，如表1 所示。

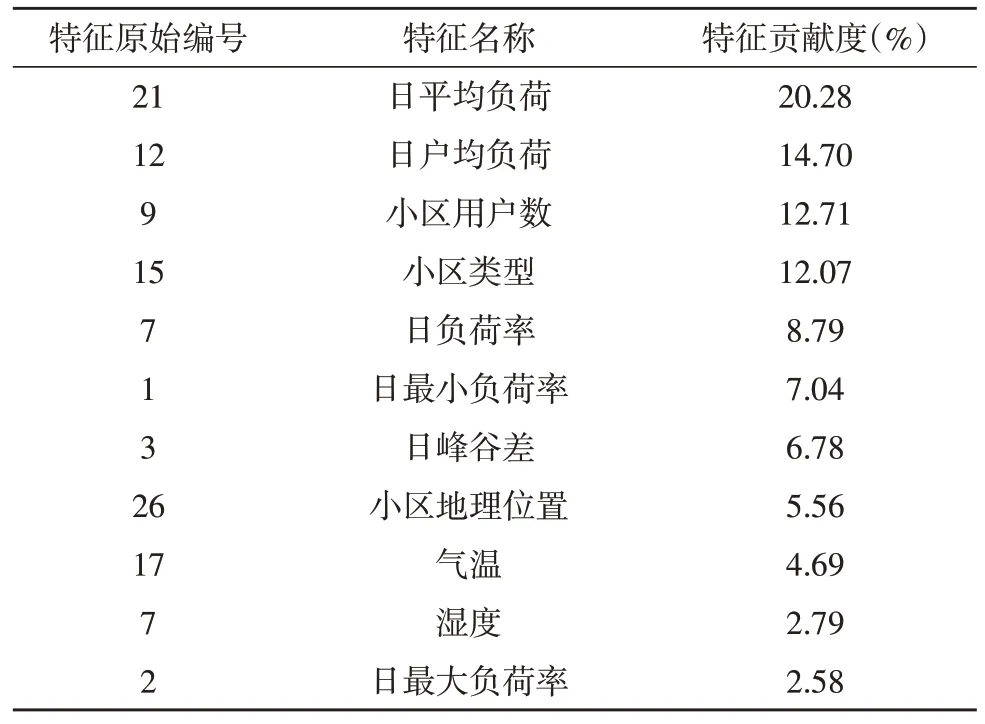
表1 文中采用的指標及貢獻度

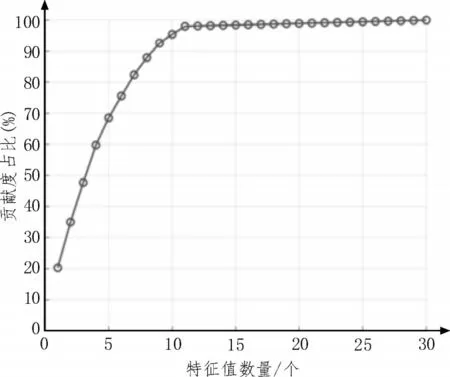
圖2 RFE特征選擇計算結果

2.2 仿真結果

該文在計算機軟件環境下對改進后的SVM、PSO算法性能進行評估。具體環境參數如表2所示。

表2 算法仿真的軟硬件環境

首先評估文中對PSO 算法的改進效果，使用標準測試函數進行驗證。所選擇的測試函數為Schaffer’s F6 及Rosenbrock，其表達式分別如下：

其中，式（17）為二維函數，最優目標值為0；式（18）則是n維函數，取n=30，最優目標值為100。

在驗證時，采用標準的PSO 算法作為對比，PSO算法中的參數與文中改進后特有參數的取值如表3所示。

表3 算法參數設置

對兩個函數分別進行100 次迭代優化，其結果如表4、5 所示。

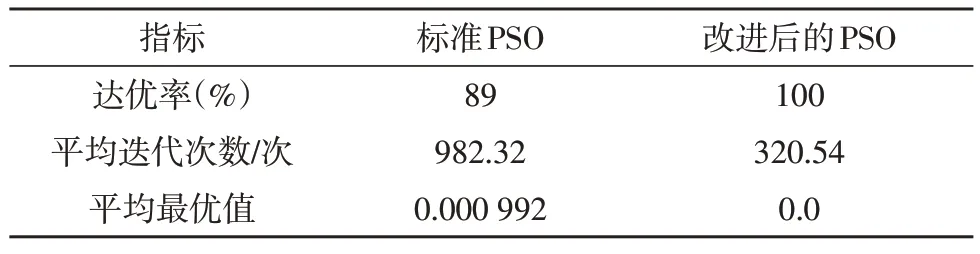
表4 Schaffer’s F6的優化結果

Schaffer’s F6和Rosenbrock分別為多峰函數和單峰函數。從表4 的結果可以看出，改進后的PSO 算法將Schaffer’s F6 的達優率提升了11%，平均迭代次數減少了661.78次，即降低67.36%；由表5可知，改進后的PSO算法將Rosenbrock的達優率提升了15.92%，平均迭代次數則降低了62.04%。綜合來看，改進后的PSO 算法對單峰函數的優化精度提升效果更為顯著，而對多峰函數的迭代效率優化效果則更好。

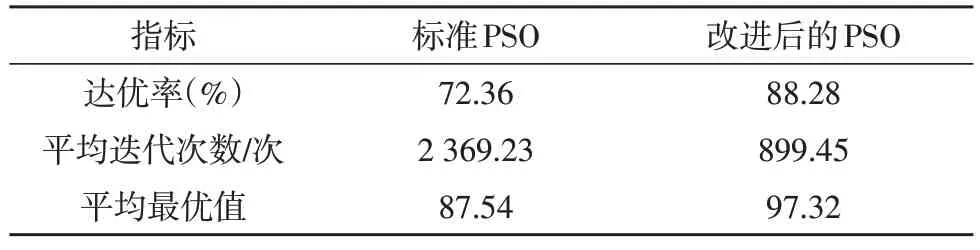
表5 Rosenbrock的優化結果

表6 給出了該文算法在用電量預測時的效果統計，其預測精度采用平均絕對誤差(Mean Absolute Error,MAE)和均方根誤差(Root Mean Square Error,RMSE)兩個指標進行評估。

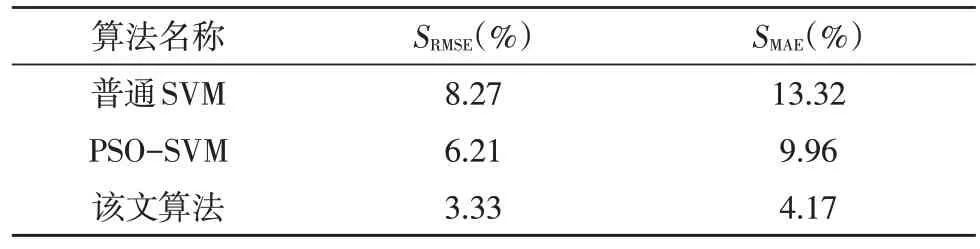
表6 不同算法的預測指標結果

從表中可以看出，采用PSO 進行參數優化的普通PSO-SVM 算法與使用傳統方式優化的SVM 算法相比，MAE 與RMSE 分別提升了3.36%和2.06%，證明了粒子群算法在參數優化時的作用。此外，該文算法相較于普通的PSO-SVM 算法，MAE 及RMSE 分別提升了5.79%和2.88%，說明該文算法在迭代效率與求解精度上均有顯著提升，這與上文的測試結果具有一致性。

3 結束語

該文使用SVM 算法的遞歸特征消除特性對用戶用電量預測的指標進行了篩選，提升了算法的訓練效率。文中還對PSO 算法進行了一定的改進，且改進后的PSO 算法收斂速度更快，預測精度更高。隨著新型電力系統建設進程的加快，該文研究算法將在電力行業取得更為廣泛的應用。