基于擴散體的聲屏障頂部結構的降噪性能

王亞晨, 王巧燕, 邱賢鋒

(中海環境科技(上海)股份有限公司, 上海 200135)

0 引 言

隨著我國城市交通運輸業的不斷發展,車流量增大帶來的交通噪聲污染問題越來越嚴重,給人們的正常生活帶來的不利影響及由此產生的一系列社會問題不容忽視。安裝聲屏障是控制道路交通噪聲的重要手段。目前應用最廣泛的聲屏障是直立式聲屏障。該類型聲屏障結構相對單一,降噪效果和防護范圍取決于其有效高度,增加屏體高度能提升聲屏障的降噪效果和防護范圍。設計特殊的聲屏障頂部結構是提升聲屏障降噪效果的一個重要方式,目前已研制出T型、圓柱型和Y型等多種形式的聲屏障頂部結構[1-2]。

聲擴散體是根據偽隨機擴散理論設計的一種聲學結構,具有良好的散射特性和一定的吸聲性能,常見的有二次余數序列擴散體(Quadratic Residue Diffuser, QRD)和原根序列擴散體(Primitive Root Diffuser, PRD),在室內聲學設計中具有廣泛應用,在聲屏障領域的研究和應用還處于起步階段[3-5]。現有的研究通常采用有限元/邊界元數值仿真計算方法,結合試驗測試進行,研究的內容主要集中在擴散體結構的散射性能或吸聲性能上,試驗條件多為平面波正向或側向入射,結構體尚處于理論設計階段[6-9]。將擴散體結構應用于聲屏障中,并檢驗其降噪性能,是一個重要研究方向。

1 聲屏障擴散體頂部結構設計

聲學擴散體的基本結構由一系列一維的槽或二維的管道組成,各槽口或管道口共同組成一個聲學平面,各槽或管道的深度按一定的偽隨機序列排列。根據亥姆霍茲共振原理,該聲學平面具有一定的擴散作用和吸聲性能。當聲波入射到擴散體結構表面時,會均勻地分散在可能的方向上,取得良好的散射特性。二次余數序列是擴散體結構設計中常用的偽隨機序列,其計算公式為

Sn=n2mod(N)

(1)

式(1)中:n為整數;N為奇素數;Sn為二次余數序列,表示為n2對N取模之后的最小非負數。二次余數序列關于n=0和n=(N-1)/2對稱,并以N為周期。N取不同的奇素數(5～13階)時對應的Sn見表1。

表1 N取不同的奇素數時對應的Sn

擴散體結構的槽深度序列dn的計算公式為

(2)

式(2)中:fr為設計頻率;c為聲波在介質中的傳播深度。由表1可知,N的階數越高,Sn序列中的最大值越大,對應的最大槽深也越大。槽深增大有助于向高頻擴展擴散體結構的散射性能,同時能使整體結構增大。頂部結構過大不僅會增大其在工程應用中實施的難度,而且會帶來安全隱患。綜合考慮,認為7階二次余數序列是合適的選擇。

擴散體擴散作用的最大有效波長λmax和最小有效波長λmin的計算公式分別為

(3)

λmin=2w

(4)

式(3)和式(4)中:dmax為擴散體中的最大槽深值;nmax為最大序列數值;w為擴散體槽寬。

由上述計算公式可知,設計頻率fr決定了擴散體結構的最大槽深,是擴散作用的最低有效頻率。據統計,道路交通噪聲的等效頻率一般在400～500 Hz[10-11],此次QRD擴散體結構的設計頻率取400 Hz。同時,為提升吸聲性能并兼顧防護效果和美觀,在擴散體結構外側設計弧形微穿孔護面板。設計的2種聲屏障擴散體頂部結構橫截面示意圖見圖1,其中:QRD-1為對稱設計,忽略了槽深序列值“0”;QRD-2為非對稱設計,具有完整的槽深序列。

圖1 設計的2種聲屏障擴散體頂部結構橫截面示意圖

根據該設計加工完成的聲屏障QRD頂部結構足尺模型的工程參數見表2。

表2 聲屏障QRD頂部結構足尺模型的工程參數

2 降噪性能仿真計算

采用基于菲涅爾理論的經驗公式無法準確計算出聲屏障頂部結構對聲場的影響,而數值計算法基于聲波的波動方程理論,能在復雜結構中取得準確的計算結果。為求解聲波入射到聲屏障頂部擴散體結構上之后的散射情況和聲場分布,采用有限元耦合邊界元法(Finite Element Method-Boundary Element Method, FEM-BEM),在頂部結構區域建立有限元模型,保證求解精度滿足要求。在計算區域外耦合邊界元模型,在計算區域內的計算完成之后,只需通過邊界元模型對邊界進行離散,即可求解出大尺度范圍內的點值[12]。

根據足尺模型的工程參數建立2種QRD結構的FEM-BEM聲學模型。為加快計算速度,按以下原則對足尺模型進行簡化:

1) 假定足尺模型為無限長的聲屏障和線聲源,建立二維聲學模型;

2) 忽略結構薄板的厚度,用聲學邊界條件替代;

3) 仿真計算的重點是聲屏障的頂部結構,估忽略頂部以下的直立屏體結構,用聲學邊界條件替代。

聲學模型邊界條件和計算域參數設置見表3。

分別對2種QRD結構的聲學模型(QRD-1和QRD-2)進行建模計算,同時對僅有微穿孔護面板而無內部QRD結構的聲屏障(以下簡稱普通聲屏障或Normal)和不設置聲屏障的空場地(noBarrier)2種工況進行建模計算,將其作為對比對象,其中普通聲屏障的總高度與QRD聲屏障的高度一致。聲學模型示意圖見圖2。

圖2 聲學模型示意圖

3 半消聲實驗室測試

在半消聲實驗室內安裝2種QRD結構聲屏障和普通聲屏障的足尺模型。聲屏障的高度和聲源位置與聲學模型一致。受實驗室內部空間大小的限制,取聲屏障的長度為6 m,從實驗室一側壁面的吸聲尖劈延伸至另一側壁面,盡量減少聲屏障兩側的繞射,使測試條件接近無限長聲屏障的工況。在聲屏障一側的中軸線上放置揚聲器,與聲屏障之間的水平距離為2 m。揚聲器為全頻段無指向性聲源,可發出100～20 000 Hz頻段內的白噪聲。

在聲屏障另一側的中軸線上設置不同距離的測點,測試3種聲屏障安裝前后的噪聲值變化。測試重點是驗證頂部結構對聲波的擴散和降噪效果,測點設置于頂部結構上方1 m處。聲源與聲屏障頂部結構外側邊緣之間可用一條直線連接,直線上方無聲屏障遮擋(聲照區),下方存在遮擋(聲影區)。測試設備布置示意圖見圖3;試驗現場照片見圖4。

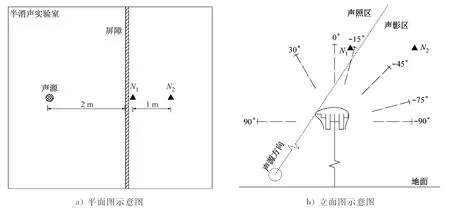
圖3 測試設備布置示意圖

4 仿真計算和結果與分析

4.1 仿真計算結果與分析

以擴散體頂部結構橫截面的幾何中心為圓心,以1 m為半徑設置一條圓截線,計算圓截線上的極坐標聲壓級值,如圖3b所示,其中:0°指向聲屏障的正上方;0°～90°為噪聲源一側;-90°～0°為接受點一側。該聲壓級反映了聲波在聲屏障頂部繞射時,散射聲場在不同方向的分布情況。計算頻率選擇擴散體結構的設計頻率(400 Hz)和2個倍頻程中心頻率(250 Hz和500 Hz)。

僅考慮頂部結構上半圓周的散射聲場分布情況,不同工況下聲屏障頂部結構上方的散射聲場分布見圖5。

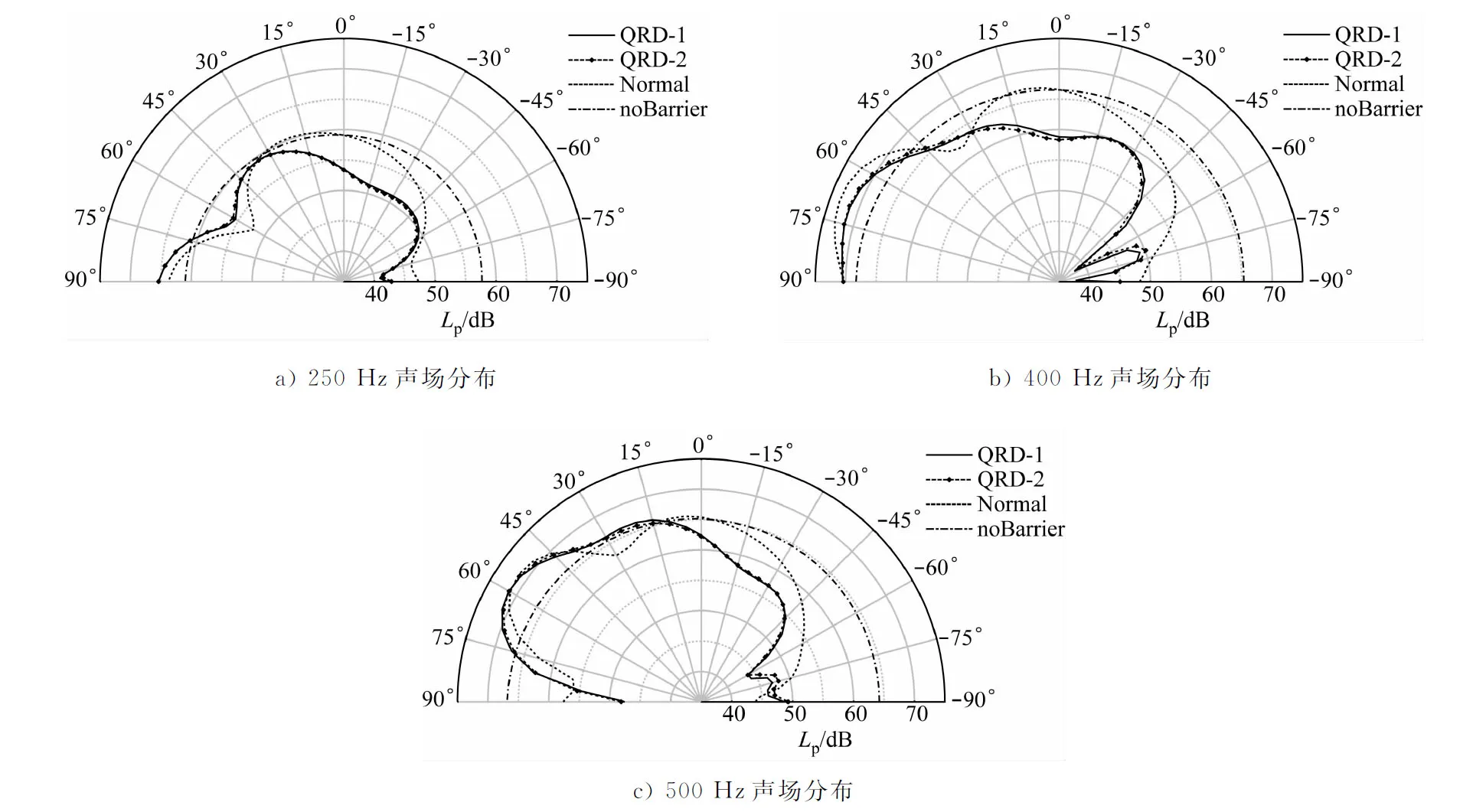
圖5 不同工況下聲屏障頂部結構上方的散射聲場分布

由圖5可知:當無聲屏障時,聲場從90°至-90°方向呈自然衰減的趨勢;設置聲屏障之后,由于聲波在屏體結構表面的反射作用和在屏障頂端的繞射作用,聲場分布發生了很大變化。

在30°～90°范圍內,2種QRD結構聲屏障和普通聲屏障的聲場大于無聲屏障的聲場,這是由于屏體結構反射造成聲能增強。QRD結構聲屏障因具有擴散特性,在聲源方向的反射聲能大于普通聲屏障。在聲波傳播越過0°角之后,普通聲屏障開始出現聲場衰減現象,衰減程度從0°至-90°方向逐漸增大。

2種QRD頂部結構在不同頻率下的聲場分布較為接近,與普通聲屏障的聲場分布存在很大差異。QRD結構聲屏障在15°角時即開始出現顯著的聲場衰減,在-75°～15°范圍內其聲場分布顯著低于普通聲屏障。QRD結構聲屏障因具有散射性能,改善了頂部區域的聲場分布,使更多的聲能向噪聲源方向反射,從而減小了繞射聲能的大小,提升了聲屏障的降噪性能。

用設置聲屏障前后相同位置處聲場聲壓級的差值表征插入損失,計算得到2種QRD結構聲屏障和普通聲屏障在聲屏障后方的插入損失(即-90°～0°范圍),結果見圖6。

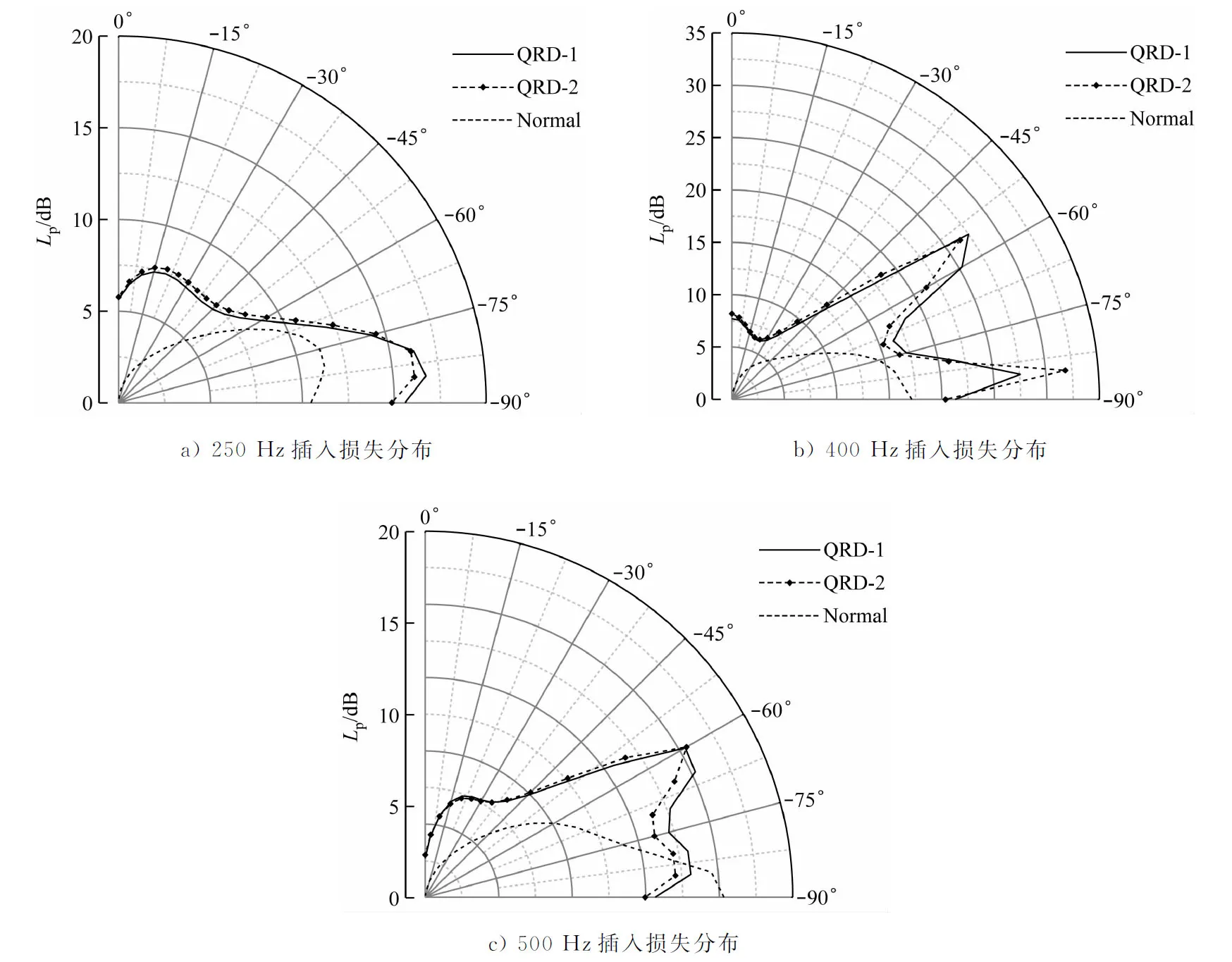
c) 500 Hz插入損失分布

由圖6可知:2種QRD結構聲屏障的插入損失接近,QRD-2型聲屏障略優于QRD-1型聲屏障,均明顯優于普通聲屏障。QRD結構聲屏障在250 Hz頻率下沿-15°和-80°方向有2個顯著的插入損失峰值,在擴散體結構設計頻率(400 Hz)下的插入損失明顯高于在其他頻率下的插入損失(在-15°、-60°和-80°方向存在顯著的損失峰值),在500 Hz頻率下的插入損失峰值出現在-15°和-60°方向。

4.2 半消聲實驗室測試結果與分析

利用測試結果對仿真計算得到的規律進行驗證,測點與聲學計算模型的對應位置如圖3b所示,測點聲壓級測試結果見表4。

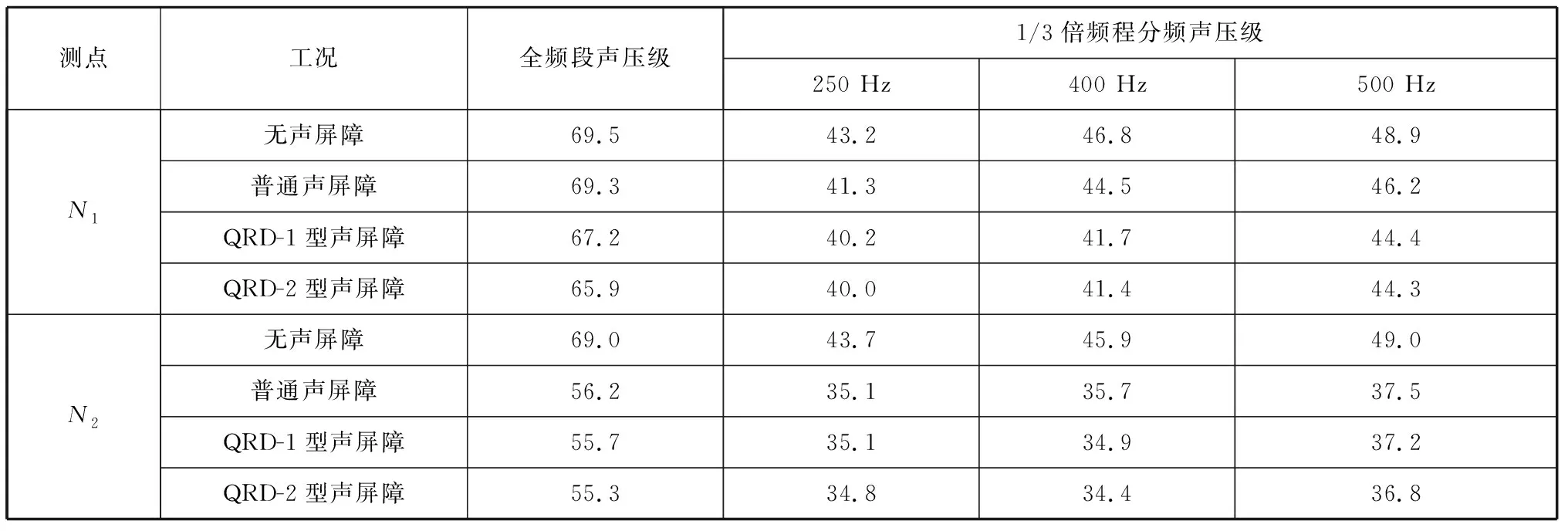
表4 測點聲壓級測試結果 單位:dB(A)

由表4可知,N1位于聲屏障聲照區,設置普通聲屏障之后,全頻段聲壓級僅降低0.2 dB,無明顯的降噪效果。從分頻聲壓級來看,在500 Hz以下的低頻區域,普通聲屏障有2 dB左右的降噪效果,但因噪聲高頻成分的掩蔽,對全頻段噪聲的降噪效果極為有限。

2種具有擴散體頂部結構的聲屏障在測點N1的聲壓級顯著低于普通聲屏障。QRD-1型聲屏障的全頻段聲壓級降低約2 dB,QRD-2型聲屏障的全頻段聲壓級降低約3 dB。從分頻聲壓級來看,QRD-2型聲屏障略優于QRD-1型聲屏障。與普通聲屏障相比,QRD結構聲屏障的降噪效果在250 Hz頻率下提高了約1 dB,在400 Hz頻率下提高了約3 dB,在500 Hz頻率下提高了約2 dB。聲屏障在擴散體設計頻率(400 Hz)下的降噪效果最優。

測點N2位于聲屏障的聲影區。3種聲屏障在全頻段聲壓級和分頻聲壓級下都有10 dB以上的降噪效果,依然呈現QRD-2>QRD-1>普通聲屏障的規律。聲影區的測點除了頂部繞射衰減,主要降噪貢獻量為屏體隔聲衰減,故在噪聲源較近的情況下3種聲屏障的降噪效果差異較小。

試驗測試結果與聲學仿真計算結果在絕對數值上存在一定的差異,但變化規律具有良好的一致性。QRD頂部結構對入射聲能存在擴散作用,能減弱繞射聲能,其突出特點是在普通聲屏障的聲照區產生了2～3 dB的降噪效果,擴大了聲影區的范圍,提升了聲屏障的整體降噪效果。

5 結 語

本文根據聲擴散體理論,針對交通噪聲的頻譜特點設計了2種具有QRD結構的聲屏障頂部結構。采用FEM-BEM建立了2種QRD頂部結構聲屏障的聲學模型,并對其進行了仿真計算,對比了其擴散性能和降噪效果。在半消聲實驗室內進行了足尺模型現場試驗測試。仿真計算結果與試驗結果具有良好的一致性。

擴散體頂部結構能有效改善聲屏障頂部的散射聲場分布,減弱其繞射聲能,從而提升聲屏障的降噪效果。具有擴散體頂部結構的聲屏障在頂端后上方約75°的扇形空間內有顯著的增強降噪效果的作用,在設計頻率(400 Hz)下的降噪效果最優。與無擴散體結構的聲屏障相比,具有擴散體頂部結構的聲屏障在非遮蔽區得到了2～3 dB的插入損失提高,在聲屏障總高不變的情況下擴大了聲影區的范圍,在實際工程中具有良好的應用前景。