創設“輻向電場”情境 命制“進動現象”試題
——以三道物理高考試題為例
程紅光 姜付錦
(1.孝感高中,湖北 孝感 432100;2.黃陂一中試題研究中心,湖北 武漢 430300)
2020年1月7日出版《中國高考評價體系》,“情境“一詞出現了40次,第一次在總綱中,“高考評價體系還規定了高考的考查載體——情境,以此承載考查內容,實現考查要求”; 在“四層”之“學科素養”中出現21次;在“關鍵能力”中出現9次;在“四翼”中出現9次,主要以“問題情境”“探究情境”等詞組呈現.2021年3月13日,教育部新版發《教育部關于做好普通高校招生工作通知》指出:“在深化考試內容改革方面,2021年高考命題要堅持立德樹人,加強對學生德智體美勞全面發展的考查和引導.要優化情境設計,增強試題開放性、靈活性,充分發揮高考命題的育人功能和積極導向作用,引導減少死記硬背和‘機械刷題’現象.”
1 2022年浙江省高考題
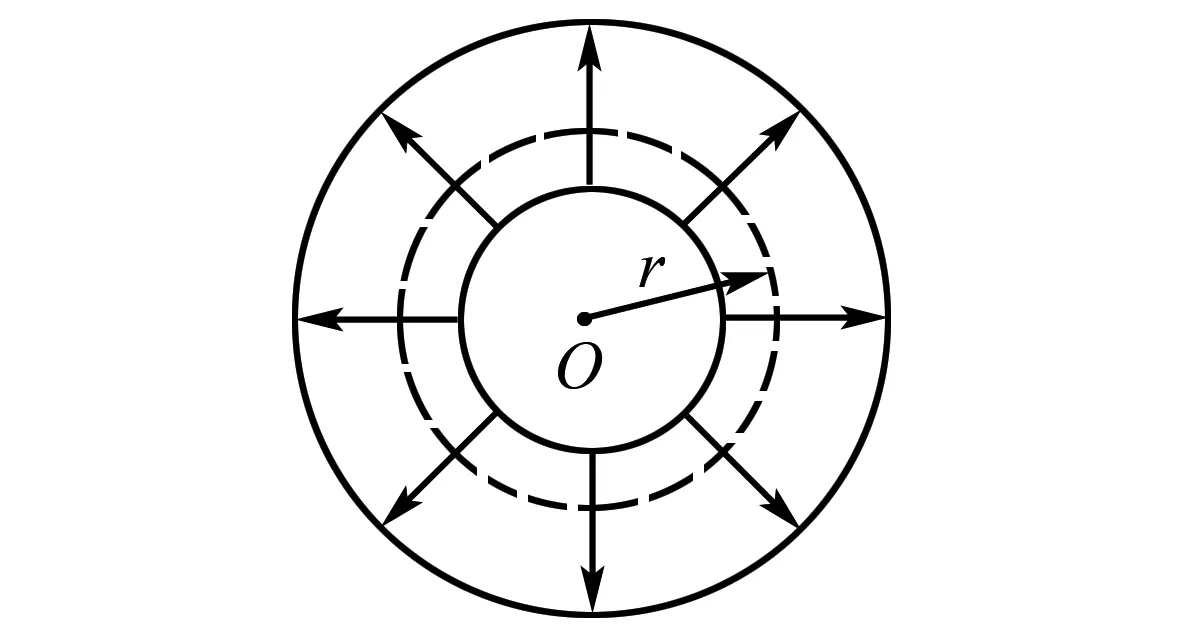
圖1 徑向電場示意圖
A.軌道半徑r小的粒子角速度一定小
B.電荷量大的粒子的動能一定大
C.粒子的速度大小與軌道半徑r一定無關
D.當加垂直紙面磁場時,粒子一定做離心運動
1.1 原題解析
這個問題定性分析很方便,設粒子質量為m、電量為q、速度為v,粒子做勻速圓周運動則
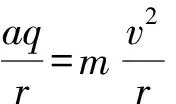
(1)
1.2 粒子與圓心最近和最遠距離
建立如圖2所示極坐標系,設帶電粒子質量、電量分別為m、-q,開始粒子速度為v0,到原點距離為ρ0,由帶電粒子運動過程總能量守恒得
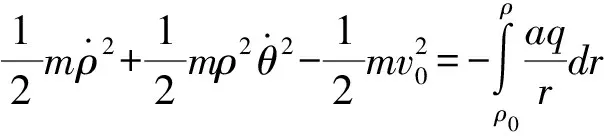
(2)
由(2)式得
(3)
若磁場垂直紙面向上,由角動量定理得
(4)
將(4)式兩邊同乘dt,并結合粒子初始狀態值定積分得
(5)
設相關物理量數值均為1,由(3)(5)兩式得
(6)
若磁場垂直紙面向下,由角動量定理得
(7)
將(4)式兩邊同乘dt,并結合粒子初始狀態值定積分得
(8)
設相關物理量數值均為1,由(7)(8)兩式得
(9)
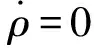
1.3 粒子進動周期
由(5)式得,當磁場垂直紙面向上時,粒子進動周期
(10)
由(8)式得,當磁場垂直紙面向下時,粒子進動周期
(11)
1.4 粒子一個周期內進動的角度
由(5)(6)兩式得,當磁場向上時一個周期內進動角
(12)
由(8)(9)兩式得,當磁場向下時一個周期內進動角
(13)
(10)(11)(12)(13)四式沒有解析解,有數值模擬解.
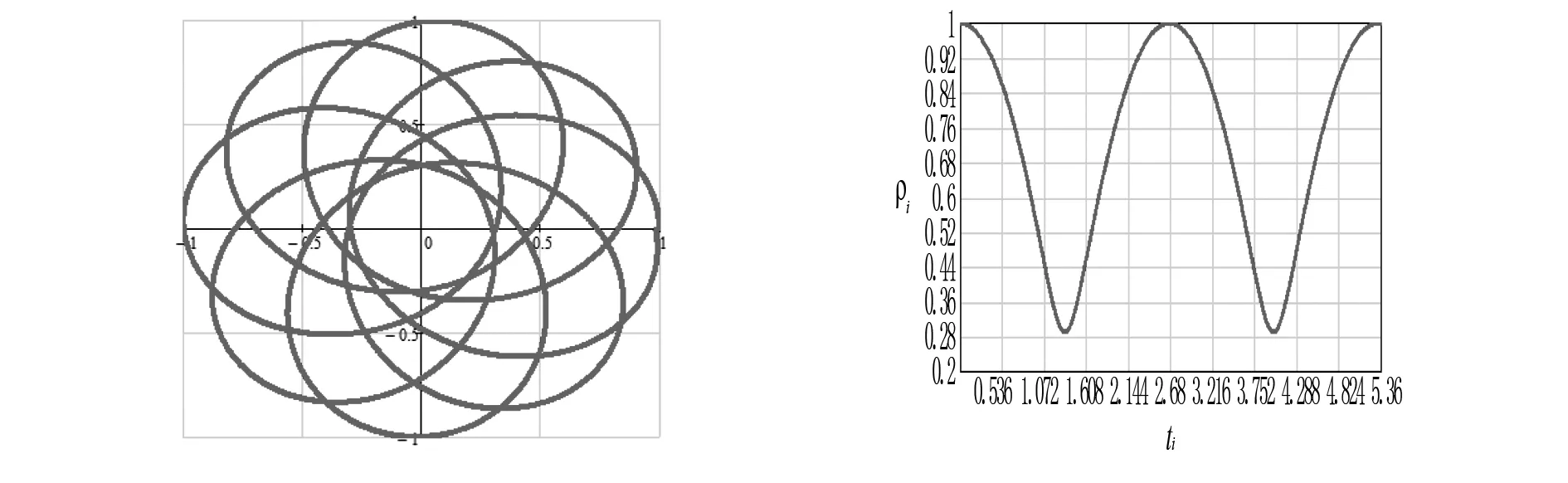
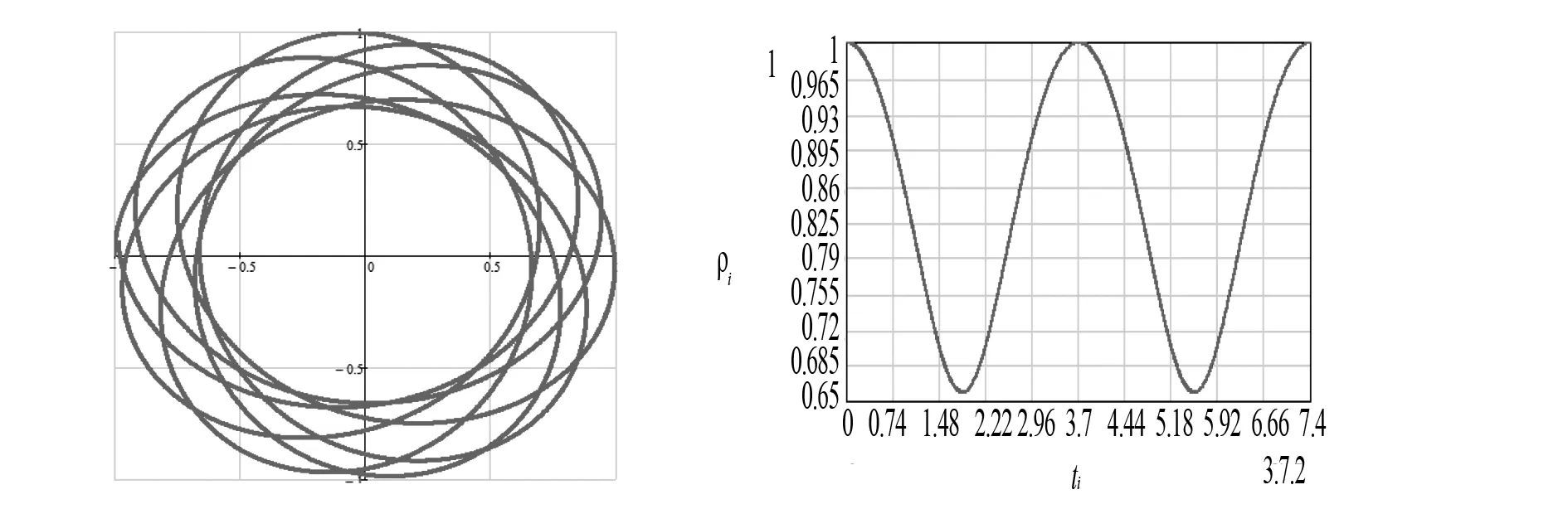
圖3 磁場垂直紙面向上時 圖4 磁場垂直紙面向上時粒帶電粒子運動軌跡圖 子到原點距離隨時間變化圖
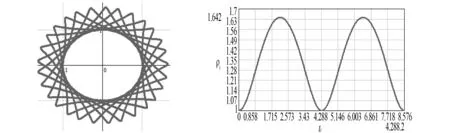
圖5 磁場垂直紙面向下時 圖6 磁場垂直紙面向下時粒帶電粒子運動軌跡圖 子到原點距離隨時間變化圖
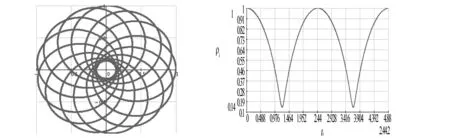
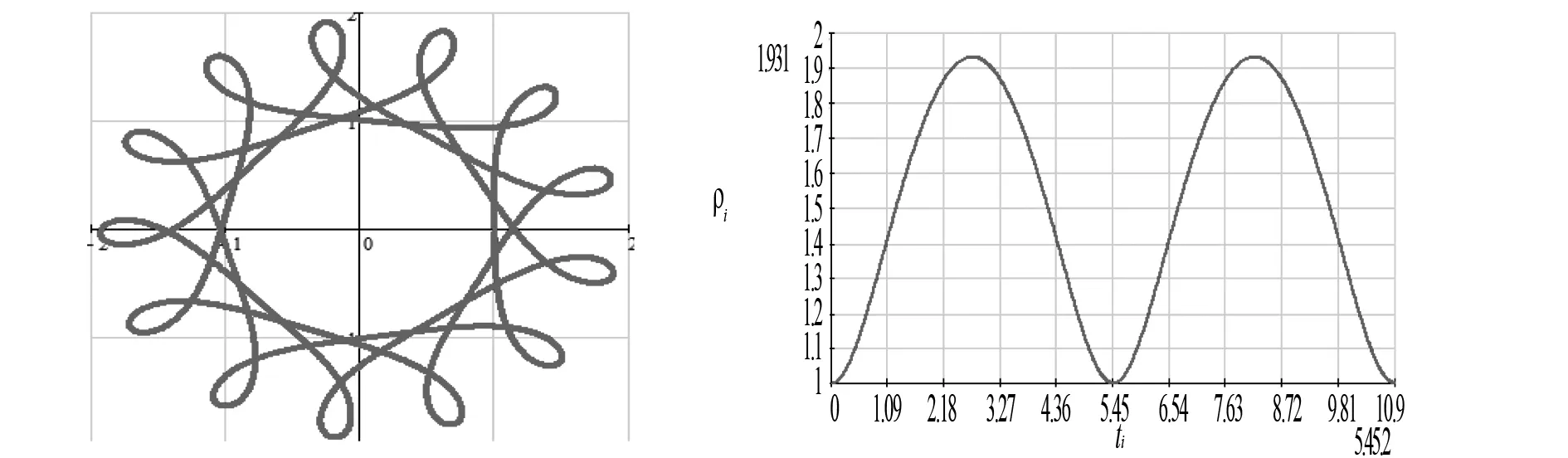
圖3和圖4是磁場垂直紙面向上時帶電粒子運動軌跡圖和粒子到原點距離隨時間變化圖;
圖5和圖6是磁場垂直紙面向下時帶電粒子運動軌跡圖和粒子到原點距離隨時間變化圖,可以發現它們的運動軌跡有進動現象特征[3].
2 2022年全國乙卷
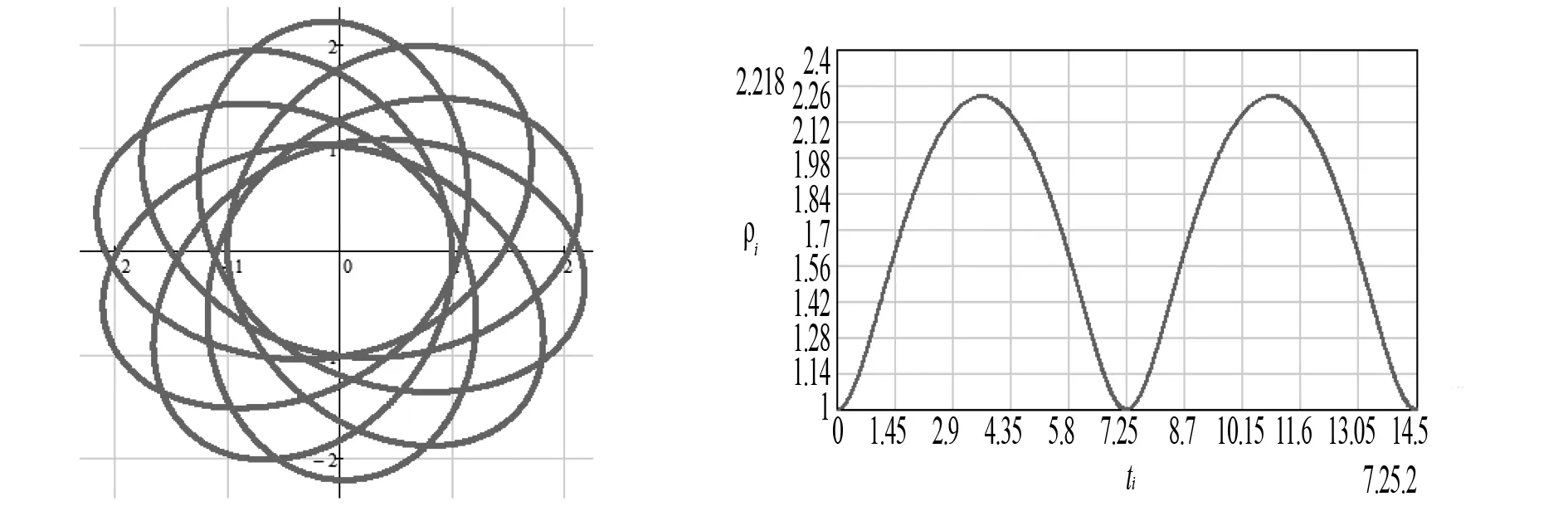
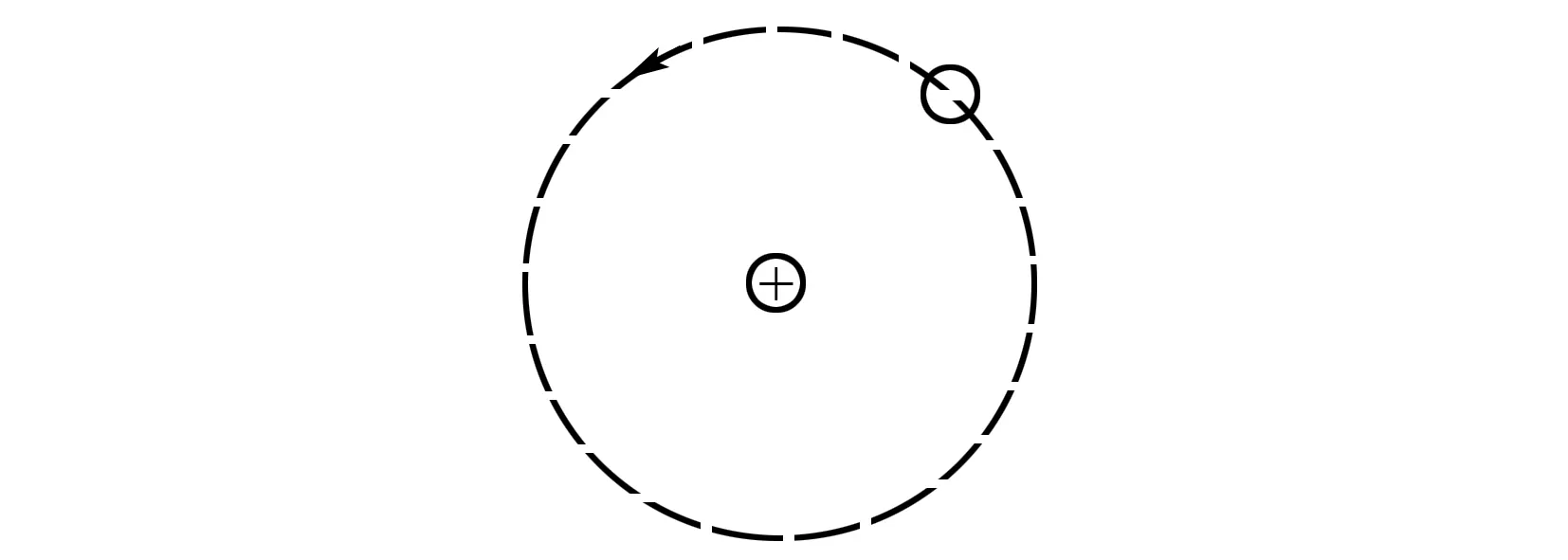
一種可用于衛星上的帶電粒子探測裝置,由兩個同軸的半圓柱形帶電導體極板(半徑分別為R和R+d)和探測器組成,其橫截面如圖7(a)所示,點O為圓心.在截面內,極板間各點的電場強度大小與其到O點的距離成反比,方向指向O點.4個帶正電的同種粒子從極板間通過,到達探測器.不計重力.粒子1、2做圓周運動,圓的圓心為O、半徑分別為r1,r2(R 圖7 A.粒子3入射時的動能比它出射時的大 B.粒子4入射時的動能比它出射時的大 C.粒子1入射時的動能小于粒子2入射時的動能 D.粒子1入射時的動能大于粒子3入射時的動能 這個問題定性分析比較容易,通過(1)式可以發現粒子做勻速圓周運動的速度相同[4];若帶電粒子受到電場力大于所需向心力時,帶電粒子做近心運動,則粒子速度變大;若帶電粒子受到電場力小于所需向心力時,帶電粒子做離心運動[5],則粒子速度變小,故答案為BD. 建立如圖2所示極坐標系,設帶電粒子質量、電量分別為m,q,開始粒子速度為v0,到原點距離為ρ0,由帶電粒子總能量守恒得 (14) 由(14)式得 (15) 由角動量守恒得 (16) 由(15)(16)兩式得 (17) 由(16)式得粒子進動周期為 (18) 由(15)(16)兩式得粒子一個周期內進動角為 (19) (18)(19)兩式均沒有解析解,有數值模擬解. 圖8 離心運動粒子運動 圖9 離心運動粒子到原點軌跡圖 距離隨時間變化圖 圖10 近心運動粒子 圖11 近心運動粒子到原點 運動軌跡圖 距離隨時間變化圖 圖8和圖9是粒子初速度大于勻速圓周運動速度時,粒子運動軌跡圖和到原點距離隨時間變化圖;圖10與11是粒子初速度小于勻速圓周運動速度時,粒子運動軌跡圖和到原點距離隨時間變化圖,它們運動軌跡具有進動現象特征. 如圖12所示,一帶負電的質點在固定正點電荷的作用下繞核做勻速圓周運動,運動周期為T0.軌道平面位于紙面內,質點的速度方向如圖12所示,現加一垂直軌道平面的勻強磁場,已知軌道半徑并不由此改變,則( ). 圖12 負點電荷繞固定正點電荷做勻速圓周運動 A.若磁場方向指向紙里,質點運動的周期將大于T0 B.若磁場方向指向紙里,質點運動的周期將小于T0 C.若磁場方向指向紙外,質點運動的周期將大于T0 D.若磁場方向指向紙外,質點運動的周期將小于T0 這個問題定性分析比較容易,若磁場指向紙里,則粒子受到的洛倫茲力背離圓心,粒子運動速度會變小,運動周期變長;若磁場指向紙外,則粒子受到的洛倫茲力指向圓心粒子運動速度會變小,運動周期變長,故答案為AD;若加上磁場后粒子的速度大小不變,則粒子運動規律如何? 建立如圖2所示極坐標系,設帶粒子質量、電量分別為m,q,正電荷電量為Q,開始粒子速度為v0,到原點距離為ρ0,由帶電粒子總能量守恒得 (20) 由(20)式得 (21) 若磁場垂直紙面向上,由角動量定理得 (22) 將(22)式兩邊同乘dt,并結合粒子初始狀態值定積分得 (23) 設相關物理量數值均為1,由(21)(23)兩式得 (24) 若磁場垂直紙面向下,由角動量定理得 (25) 將(25)式兩邊同乘dt,并結合粒子初始狀態值定積分得 (26) 設相關物理量數值均為1,由(21)(26)兩式得 (27) 由(24)式得,當磁場垂直紙面向上時粒子進動周期 (28) 由(27)式得,當磁場垂直紙面向下時粒子進動周期 (29) 由(21)(24)兩式得,當磁場向上時,一個周期內進動角 (30) 由(26)(27)兩式得,當磁場向下時,一個周期內進動角 (31) (28)(29)(30)(31)四式沒有解析解,有數值模擬解. 圖13 洛倫茲力指向原點 圖14 洛倫茲力指向原點時粒子時粒子運動軌跡圖 到原點距離隨時間變化圖 圖15 洛倫茲力背離原 圖16 洛倫茲力背離原點時粒子點時粒子運動軌跡圖 到原點距離隨時間變化圖 圖13和圖14是開始時粒子受到洛倫茲力指向原點時,粒子運動軌跡圖和粒子到原點距離隨時間變化圖[6];圖15和圖16是開始時粒子受到洛倫茲力背離原點時,粒子運動軌跡圖和粒子到原點距離隨時間變化圖[7];故若帶負電粒子在加了磁場后的速率不變,則其運動軌道不再是一個圓周,會不斷的近心、離心…(或離心、近心…),具有進動現象特征. 浙江卷試題只要學生能正確分析電場力與向心力關系不難做出,至于加了磁場后的情況定性分析即可;全國乙卷也只是定性分析這種輻向電場的特點,考察點基本上和浙江卷類似,但是乙卷中粒子3和粒子4的運動軌跡應該具有進動現象特征,但題中圖7(b)中并沒有體現出粒子運動軌跡進動現象特征,容易讓人誤以為是圓錐曲線;2007年全國卷試題在加磁場后粒子勻速圓周運動半徑沒有變化,故粒子速度會發生變化,運動周期也會發生變化,學生要做對也不難;若加磁場后粒子速率不變,則粒子運動軌跡具有進動現象特征;2022年浙江卷比全國乙卷更具開放性和靈活性,需要學生建立運動模型后才能進行全面分析.三道題通過提供輻向電場(或點電荷電場)問題情境,讓帶電粒子開始做勻速圓周運動,分析在加上磁場后粒子運動規律,體現“試題提供問題情境,綜合考查物理建模和物理分析能力”情境化命題特點.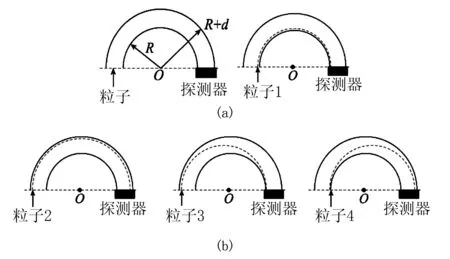
2.1 原題解析
2.2 粒子與原心的最近和最遠距離
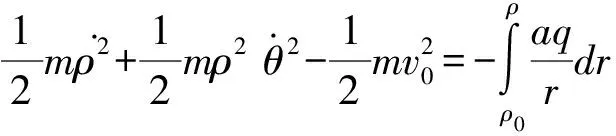
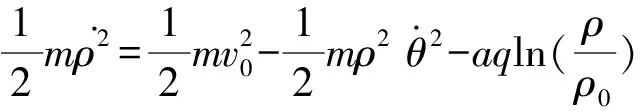
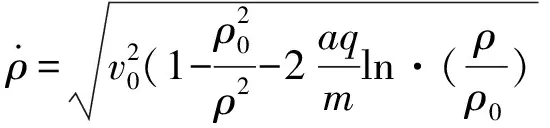
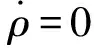
2.3 粒子進動周期
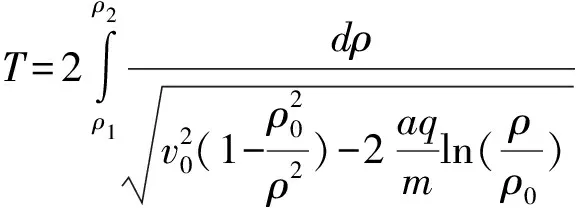
2.4 粒子一個周期內進動的角度
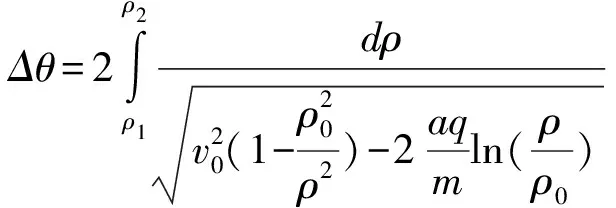
3 2007年全國卷
3.1 原題解析
3.2 粒子與原心的最近和最遠距離
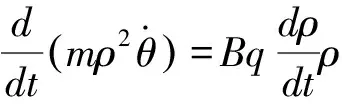
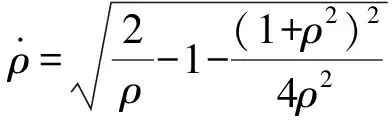
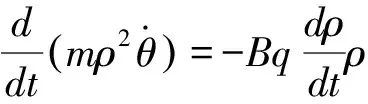
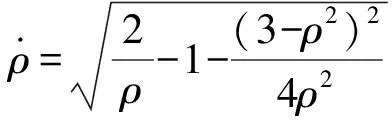
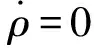
3.3 粒子進動周期
3.4 粒子一個周期內進動的角度