不規則混凝土殼體收縮徐變效應的有限元分析

熊高亮

(江西省交通設計研究院有限責任公司,江西 南昌 330052)

0 引言

收縮徐變是混凝土本身的固有特性,會導致混凝土結構應力和變形隨時間而改變,對結構的受力性能及長期變形影響很大[1],有時甚至成為導致結構物開裂破壞的關鍵因素,特別是對于大體積、大面積混凝土結構,收縮徐變效應更為顯著。

混凝土結構收縮徐變的研究較為復雜,國內外對此展開了很多研究,張運濤等在高性能混凝土收縮徐變模型試驗研究的基礎上,開展了自然環境下高性能混凝土雙懸臂構件的長期性能試驗研究[2],李達等對簡支組合梁在長期變形下混凝土的收縮模式進行了相關研究[3],熊學玉等[4]對某預應力梁在混凝土收縮徐變效應作用下的真實反應進行測試并分析實測數據,鄭怡等通過實驗研究了機制砂混凝土梁收縮徐變[5],Warner,Robert F[6]和Asamoto,Shingo等[7]對混凝土梁的徐變效應進行了相關分析。

國內外對混凝土收縮徐變的研究對象多為橋梁和規則的梁、板結構,對不規則混凝土殼體的收縮徐變效應的研究相對較少。本文以一實際工程為背景(見圖1),結合收縮和徐變等相關知識,運用有限元軟件,研究該不規則混凝土殼體在自重作用下的收縮徐變效應,將其應力及應變情況與不考慮收縮徐變時的結果進行對比分析,總結收縮徐變效應對該殼體的影響,為類似結構的設計提供一定的參考。

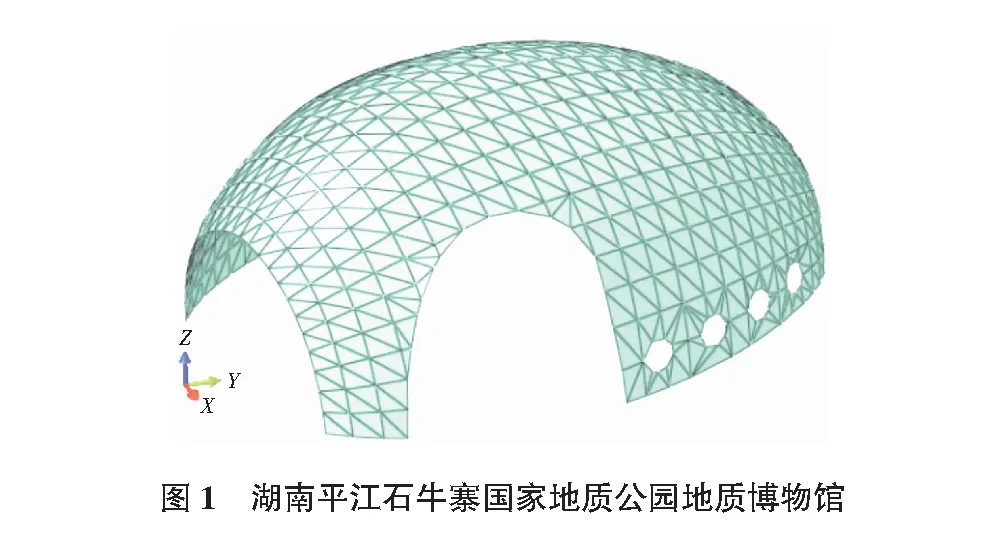
1 混凝土收縮徐變的理論計算

1.1 收縮應變的計算

混凝土的收縮是指混凝土在凝結硬化及使用過程中,由于混凝土內部水分變化、化學反應及溫度變化等所引起的體積減小的現象。混凝土第一年的收縮應變約為(0.2-0.4)×10-3,其80%～90%可在前6個月內完成,一年以后收縮仍有發展,但不明顯[8],因此本文研究殼體竣工一年后的收縮效應,混凝土的收縮應變可按式(1)—式(5)計算[9]:

εcs(t,ts)=εcs0·βs(t-ts)

(1)

εcs0=εs(fcm)·βRH

(2)

εs(fcm)=[160+10βsc(9-fcm/fcm0)]×10-6

(3)

βRH=1.55×[1-(RH/RH0)3]

(4)

(5)

其中,t為計算考慮時刻的混凝土齡期,d;ts為收縮開始時的混凝土齡期,d,可假定為3 d～7 d;εcs(t,ts)為收縮時間發展的系數;fcm為強度等級C20—C50混凝土在28 d齡期時的平均立方體抗壓強度,MPa,fcm=0.8fcu,k+8 MPa;fcu,k為齡期28 d,具有95%保證率的混凝土立方體抗壓強度標準值,MPa,本文為35 MPa;βRH為與年平均相對濕度相關的系數,式(1)—式(4)適用于40%≤RH<90%;RH為環境年平均相對濕度,%;βsc為依水泥種類而定的系數,對一般的硅酸鹽類水泥或快硬水泥,βsc=5.0;h為構件理論厚度;h=2A/u,A為構件截面面積,u為構件與大氣接觸的周邊長度,本文計算得h=125 mm。

其他相關參數取值如下RH0=100%,h0=100 mm,t1=1 d,fcm0=10 MPa;本文中t=365 d,ts=3 d,RH取55%,通過以上公式計算可得,εcs(t,ts)=0.351×10-3,此結果與前文提到的混凝土第一年的收縮應變約為(0.2～0.4)×10-3相符,表明結果的合理性。

本文在研究殼體的收縮效應時,結合溫度變化等效混凝土收縮[10]的思想,由計算得到的收縮量,通過ε=αΔT(其中,α為膨脹系數,取1×10-5/℃;T為溫度,℃,轉換為溫度的變化來等效收縮作用。

1.2 徐變系數的確定

混凝土在長期持續荷載作用下,應力不變,變形也會隨時間而增長,這種現象稱為混凝土的徐變。徐變在早期發展較快,一般在最初六個月內可完成最終徐變的大部分(約70%～80%),一年可完成約90%,最終總徐變應變值為瞬時應變的2倍～4倍。

通常混凝土的徐變采用徐變系數φ(t,t0)來描述[11]。由規范查得混凝土的徐變系數可按式(6)—式(12)計算:

φ(t,t0)=φ0·βc(t-t0)

(6)

φ0=φRH·β(fcm)·β(t0)

(7)

(8)

(9)

(10)

(11)

(12)

其中,t0為加載時的混凝土齡期,d;t為計算考慮時刻的混凝土齡期,d;φ(t,t0)為加載齡期為t0,計算考慮齡期為t時的混凝土徐變系數;φ0為名義徐變系數;βc為加載后徐變隨時間發展的系數。

由于徐變是一種長期效應,而對于本文所研究的殼體來說,自重作用在殼體上的時間最為長久,所以本文僅研究殼體在自重作用下的徐變效應。在本文當中,RH0=100%,h0=100 mm,t1=1 d,fcm0=10 MPa;t=365 d,t0=3 d,h=125 mm,RH取55%,fcm=36 MPa,由以上公式計算得φ(t,t0)=3.120。

本文基于有效模量法[12]的思想,在其基礎上進行一定的改進,在有限元分析時結合Abaqus中的混凝土塑性損傷模型,將按照有效模量法計算出的彈性模量代替該模型中初始彈性模量,進而對不規則混凝土殼體的徐變效應進行研究。

2 殼體在收縮作用下的有限元分析

2.1 收縮作用下殼體內表面的應力分析

在收縮作用下,不規則混凝土殼體內表面的最大主應力云圖如圖2,圖3所示。

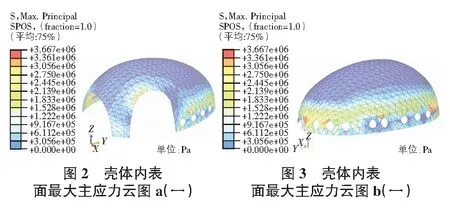
從圖2,圖3中可以看出,在收縮作用下,不規則混凝土殼體頂部的最大主應力較小,一般都低于0.306 MPa,而殼體最底部受約束的部位,在殼體收縮的過程中受到較大的約束作用,混凝土處于明顯的受拉狀態,最大主應力較大,大部分都超過了0.611 MPa;在門窗洞口附近部分區域由于局部幾何形狀的原因存在應力集中現象,最大主應力較大,其中有一些部位的最大主應力值超過了3.056 MPa。整個殼體內表面應力的最大值3.667 MPa,位于圖3殼體的最左端,此處不僅離底端約束近,且在窗洞口附近,同時此處的曲率相對較大,所以當混凝土殼體發生整體收縮時,此處的最大主應力值最大。

2.2 收縮作用下殼體外表面的應力分析

在收縮作用下,不規則殼體外表面的最大主應力云圖如圖4,圖5所示。

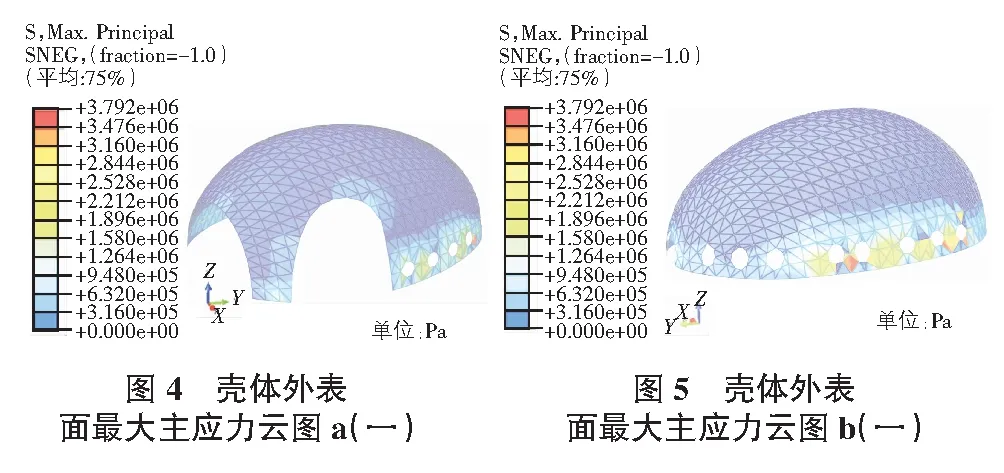
從圖4,圖5中可以看出,在收縮作用下,殼體的外表面最大主應力較大的部位主要分布在殼體下端的窗洞口附近,應力值一般都大于1.580 MPa,這些區域由于洞口的存在,收縮量相對更大,因而在殼體發生收縮時,產生較大的拉應力;除此以外的大部分區域,最大主應力值都相對較小,均低于0.632 MPa;整個外表面的最大主應力值為3.792 MPa,位于圖4中殼體最右邊的窗洞口的右下端。通過以上分析,可以發現,該殼體受收縮作用的影響較為明顯,在收縮作用下,殼體表面的最大主應力值較大,在工程設計中不容忽視。

3 殼體在徐變作用下的應力應變分析

3.1 殼體考慮徐變作用時的有限元分析

通過有限元計算,在自重作用下,考慮混凝土徐變效應后,該不規則混凝土殼體內外表面的最大主應力云圖如圖6—圖9所示。

在圖6中,兩個大洞口的底端和頂端的小部分區域,在自重荷載的作用下發生較大的變形,殼體內表面的最大主應力相對較大,其值在1.188 MPa以上;其余部分的最大主應力分布情況較為均勻,且應力值較小,大部分不超過0.198 MPa。整個殼體在自重作用下內表面最大主應力的最大值為2.377 MPa,對應部位見圖6中殼體左邊大洞口的右下端。在圖7中,只有最右下端靠近洞口的小部分區域的最大主應力值較大,最大主應力值為0.990 MPa;其他區域的最大應力值均較小,一般低于0.396 MPa。

圖8中,殼體側面的最大主應力值相對較大,該區域的最大主應力值都在0.267 MPa以上,而殼體頂端區域和最下端區域的最大主應力值較小,其最大主應力均小于0.177 MPa。在兩個大洞口的左右兩側區域的最大主應力值相對較大,該區域的最大主應力值均在0.445 MPa以上;特別是兩個大洞口之間的區域,該處的最大主應力值比殼體其他區域的最大主應力值都要大,一般都超過了0.533 MPa,在自重作用下,整個殼體外表面最大主應力值最大的部位即位于該區域,其值為1.067 MPa。在圖9中,圖中最右端靠近大洞口附近區域的最大主應力值較大,其中最大值為0.889 MPa;沿殼體側面自右向左逐漸減小,一直減小到圖中最左端部位的0.267 MPa;而殼體頂部和底部的最大主應力值相對較小,一般小于0.178 MPa。

3.2 徐變對殼體應力應變的影響

運用有限元軟件計算該不規則混凝土殼體在不考慮徐變效應時,內外表面的最大主應力情況,并將其與前文考慮徐變作用時殼體內外表面的最大主應力云圖進行對比分析。定義圖8中殼體左邊大洞口邊界線自左向右為路徑a(如圖8紅線所示),分析殼體內外表面最大主應力在考慮徐變前后沿路徑a的變化。

從圖10,圖11中可以看出,考慮徐變作用前后,殼體內外表面最大主應力沿路徑a的分布曲線走勢大致相同,只是考慮徐變后的應力值普遍比未考慮徐變時的應力值要大,由此也可以看出徐變效應對建筑物的不利影響。現將殼體在自重作用下考慮和未考慮徐變作用時,內外表面的最大主應力值進行對比,見表1。

表1 徐變對內外表面最大主應力的影響 MPa

通過對比發現,考慮徐變效應后,殼體內外表面的最大主應力值的峰值都有所增大,內表面增大了0.405 MPa,外表面增大了0.164 MPa。

調取考慮徐變前后殼體在最大主應力方向上的應變值進行對比,得到的具體情況見表2。

表2 徐變對內外表面最大應變值的影響

對比發現,考慮殼體的徐變作用以后,最大應變值明顯增大,殼體內表面的最大應變值是沒有考慮徐變時最大應變值的3.165倍,外表面的最大應變值是沒有考慮徐變時最大應變值的2.865倍。由此可以看出,徐變對于該混凝土殼體的作用很明顯,使得該殼體的應力應變明顯增大,在實際工程設計中應當給予重視。

4 結論

本文通過運用與收縮相關的理論知識,計算出一個不規則混凝土殼體建成一年后的收縮應變,運用降溫等效的思路對殼體進行收縮作用下的有限元分析;通過規范提供的方法計算出該殼體建成一年后混凝土的徐變系數,基于有效模量法的思想計算該殼體的徐變效應,得出以下結論:

1)不規則混凝土殼體在建成一年后,收縮應變為0.351×10-3。在收縮作用下,不規則混凝土殼體頂部的最大主應力較小,而下部四周門窗洞口附近及殼體最底部受約束處的最大主應力較大,整個殼體的最大主應力值為3.792 MPa,位于殼體外表面大窗洞口的右下端。

2)不規則混凝土殼體建成一年后對應的徐變系數為3.120,在自重作用下,考慮徐變效應后,殼體內表面的最大主應力在兩個大洞口的底端和頂端的小部分區域較大,最大值2.377 MPa;殼體外表面兩個大洞口之間的區域的最大主應力值較大,外表面最大主應力值為1.067 MPa。

3)考慮徐變效應前后,殼體表面的最大主應力分布情況大致相同,但考慮徐變效應后,殼體內外表面的最大主應力值的峰值普遍有所增大,內表面最大主應力的峰值增大了0.405 MPa,外表面的峰值增大了0.164 MPa。在考慮徐變效應以后,殼體內表面的最大應變值是沒有考慮徐變時最大應變值的3.165倍,外表面的最大應變值是沒有考慮徐變時最大應變值的2.865倍。