挖掘“隱圓”巧解向量最值問題

陳存勤

(江蘇省啟東中學,江蘇 啟東 226200)

高考試題或者模擬試題中,經常出現考查向量最值的問題,這類題目難度較大,常常找不到解題的切入點,或者運算量過大.那么,如何解決這一類問題呢?這類試題往往隱藏著圓的背景,如果我們能夠通過分析已知條件,或者將其進行轉化,把題目中隱藏的圓揭示出來,然后,在此基礎上,利用圓中的特殊線或者特殊位置,就可以幫助我們解決這類試題[1].

1 建立坐標系找出“隱圓”

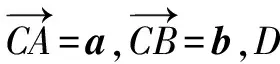
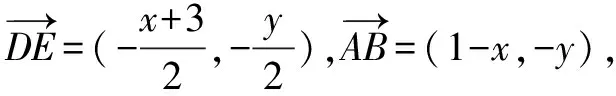
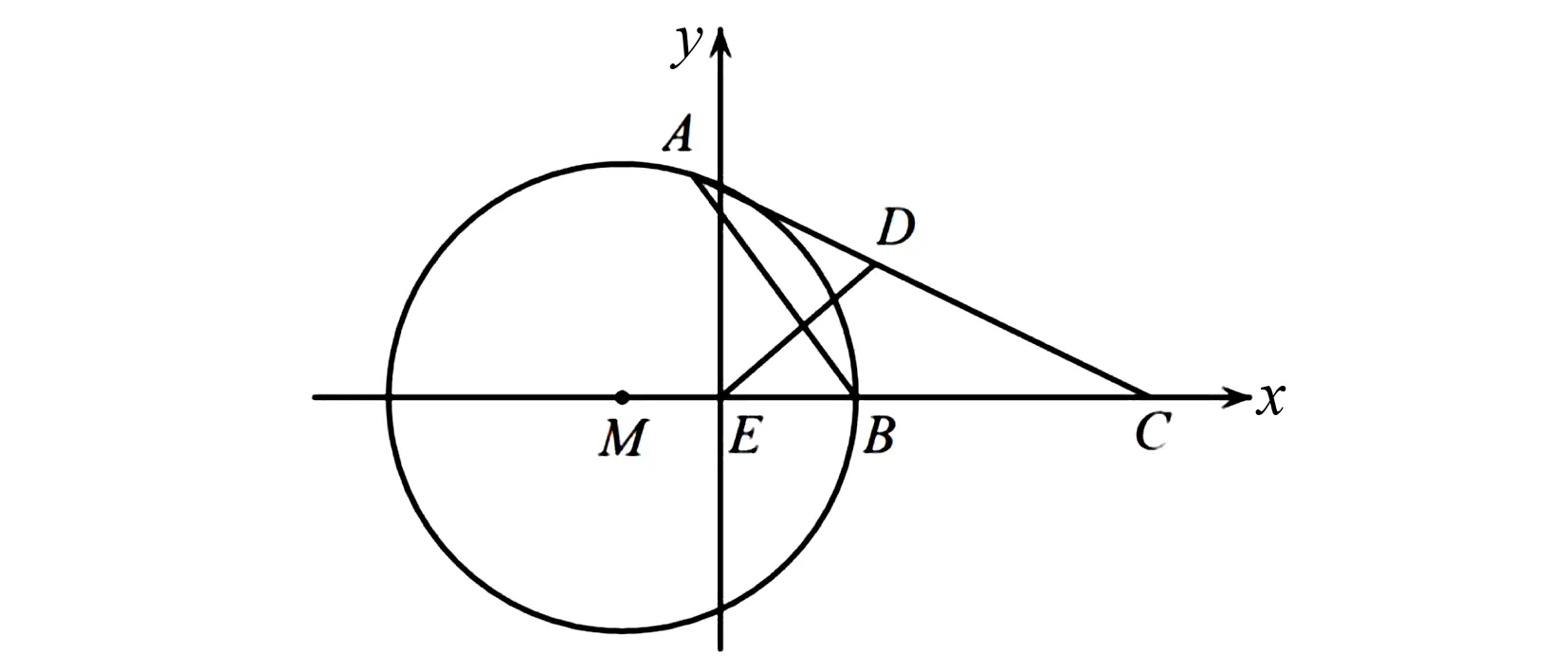
圖1 A的軌跡為圓

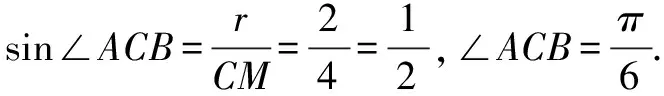
例2已知平面向量a,b,c滿足a⊥b,且|a|=|b|=2,|c-a-b|=1,則|c-a|+2|c-b|的最小值為( ).

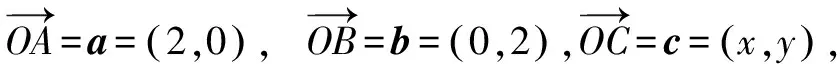
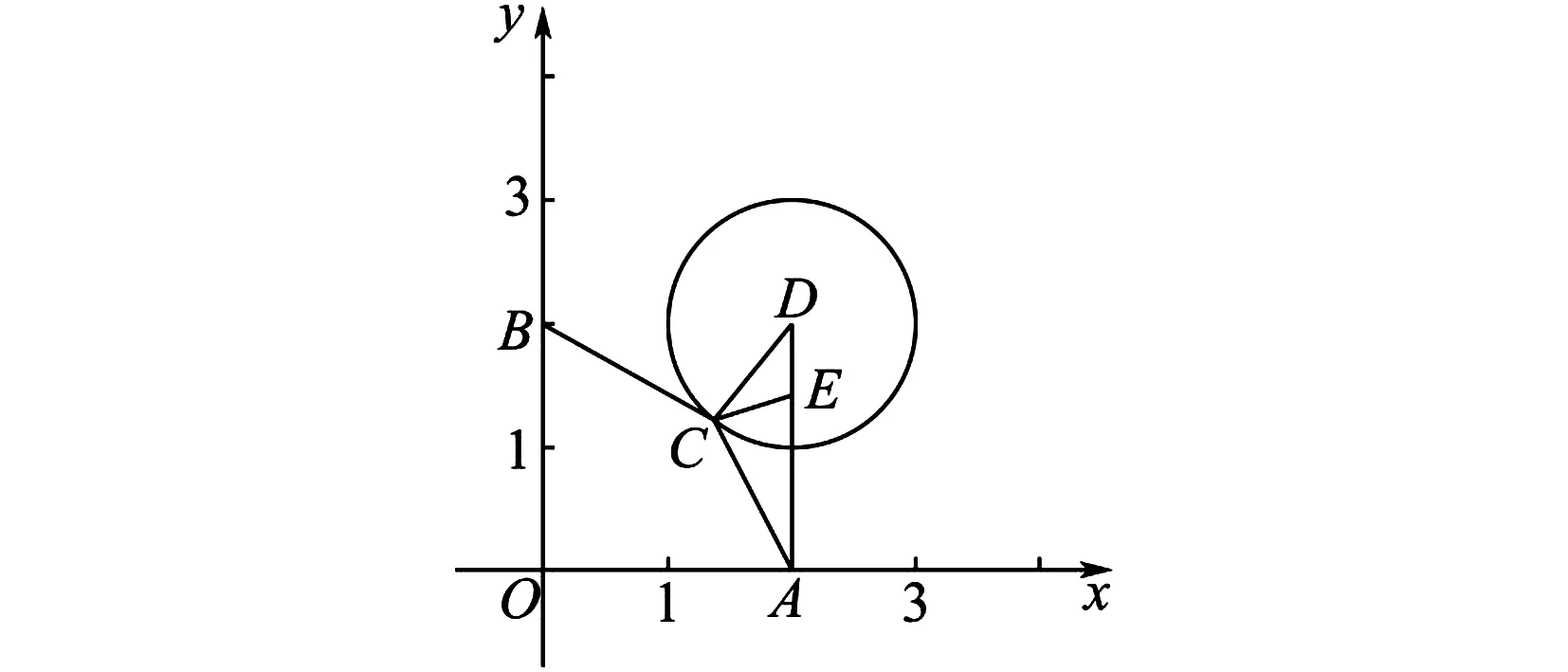
圖2 動點C在圓上

由|c-a-b|=1得(x-2)2+(y-2)2=1,

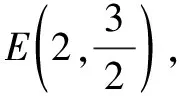
又∠CDE=∠ADC,

∴△ECD∽△CDA,

在對工程項目進行測量的過程中，需要對測量設備進行前期檢查，確保測量全過程的穩定。因此，建議采取以下幾方面的措施進行控制：(1)精準求解測量的轉換參數，配備高等級的數據轉換控制點，保障各控制點均勻分布，爭取測區全覆蓋；(2)采用先進的GPS 信號接收器，如雙星或三星GPS接收器，縮短測量時間，提高定位精度，加快測量進度；(3)增加測量區域控制點的設置，保證轉換控制點覆蓋整個測區，使測量結果更具客觀性和準確性，保障測量數據的真實性和可信性；(4)必要時增加測量次數，多次測量可有效消除系統性測量誤差，進行提高測量精度，提升測量數據可靠性。

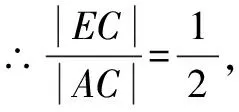
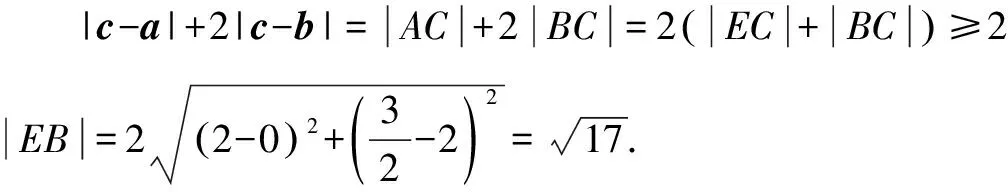
點評建立坐標系后,發現點C的軌跡方程是圓,利用三角形的相似及兩點之間直線段最短,即可獲解.

2 根據向量模長找出“隱圓”

例3(2016年陜西省數學競賽)已知a,b,c是同一平面內的三個單位向量,且a⊥b,則(c-a)·(c-b)的最大值是( ).

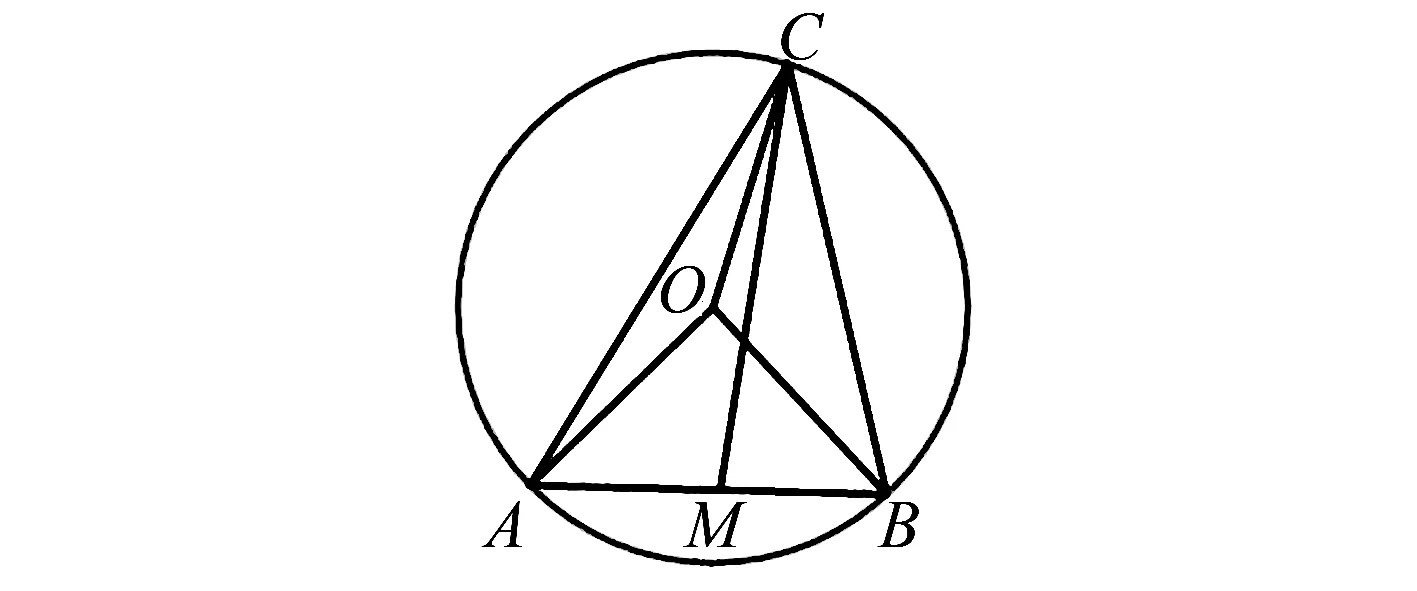
圖3 單位圓

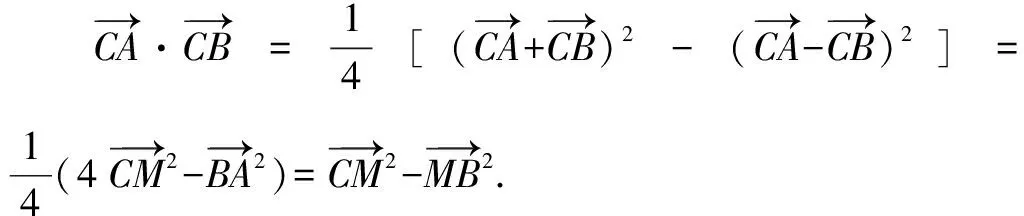
例4已知平面向量a,b,c滿足|a-b|=4,(a-c)·(b-c)=-3,則c·(a+b)的最小值為( ).

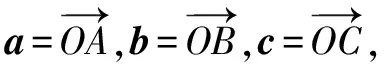
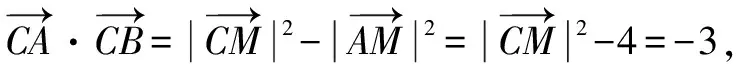
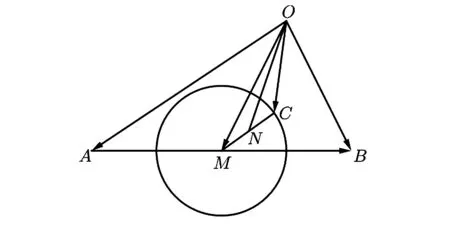
圖4 C的軌跡為圓

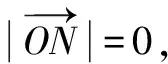
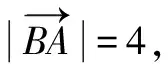
3 根據幾何特征找出“隱圓”

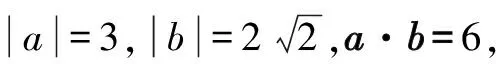
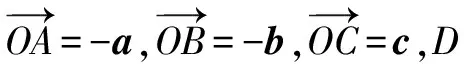
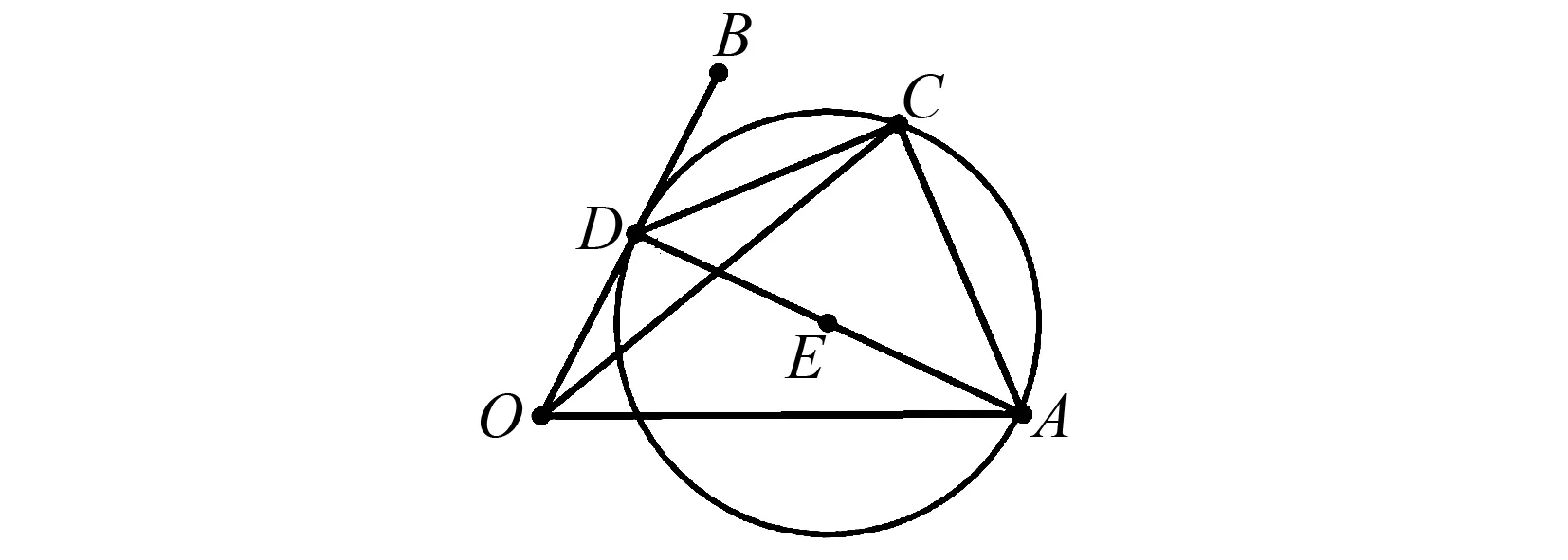
圖5 以AD為直徑的圓

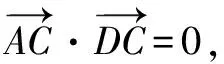
解析由b2-4e·b+3=0得b2-4e·b+3e2=0?(b-e)·(b-3e)=0即(b-e)⊥(b-3e).由此可找出“隱圓”,如圖6所示.

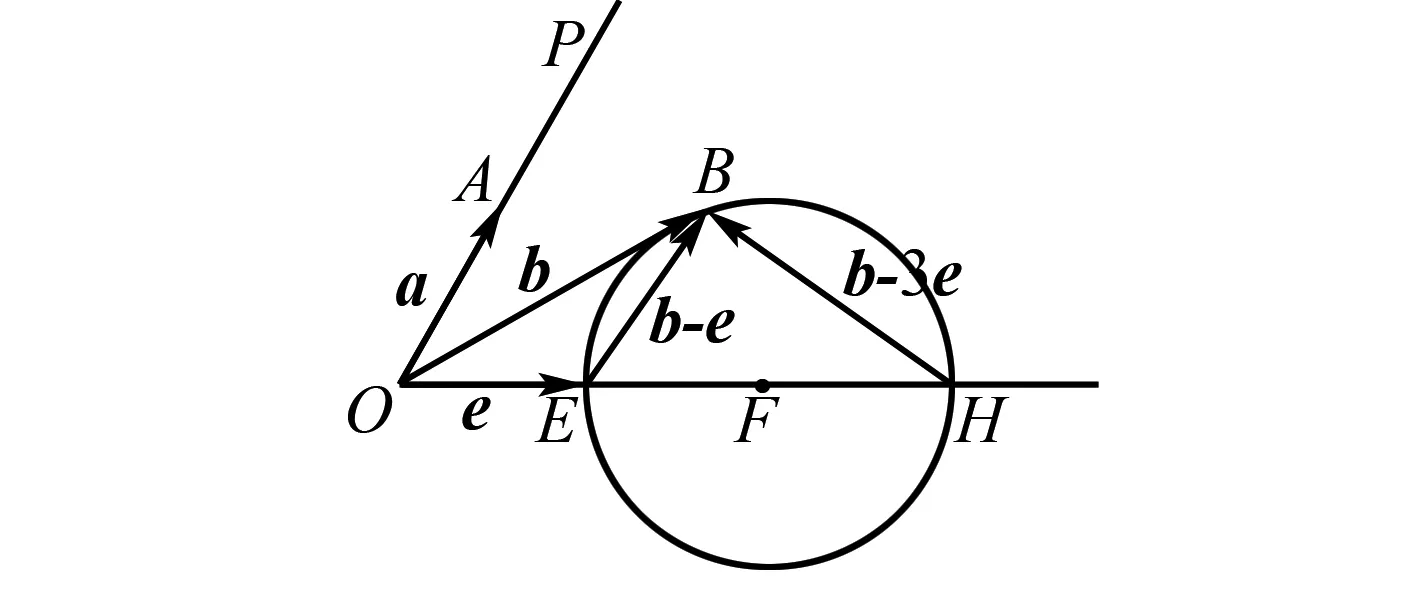
圖6 B的軌跡為圓

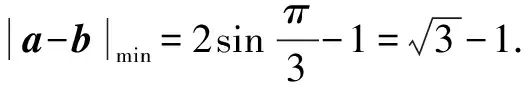
點評本題關鍵是根據e是單位向量,把b2-4e·b+3=0得轉化為b2-4e·b+3e2=0,從而得到(b-e)⊥(b-3e),即可找出“隱圓”.

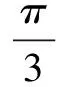
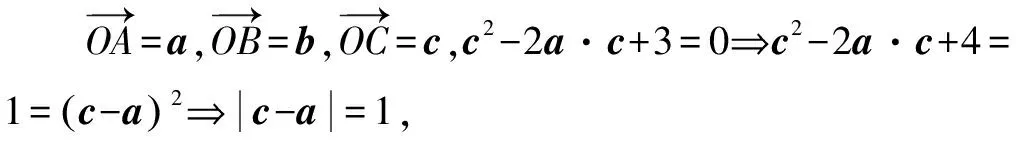
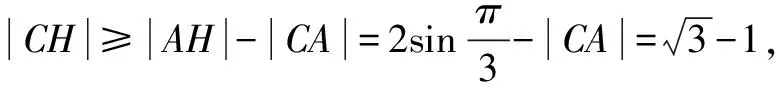
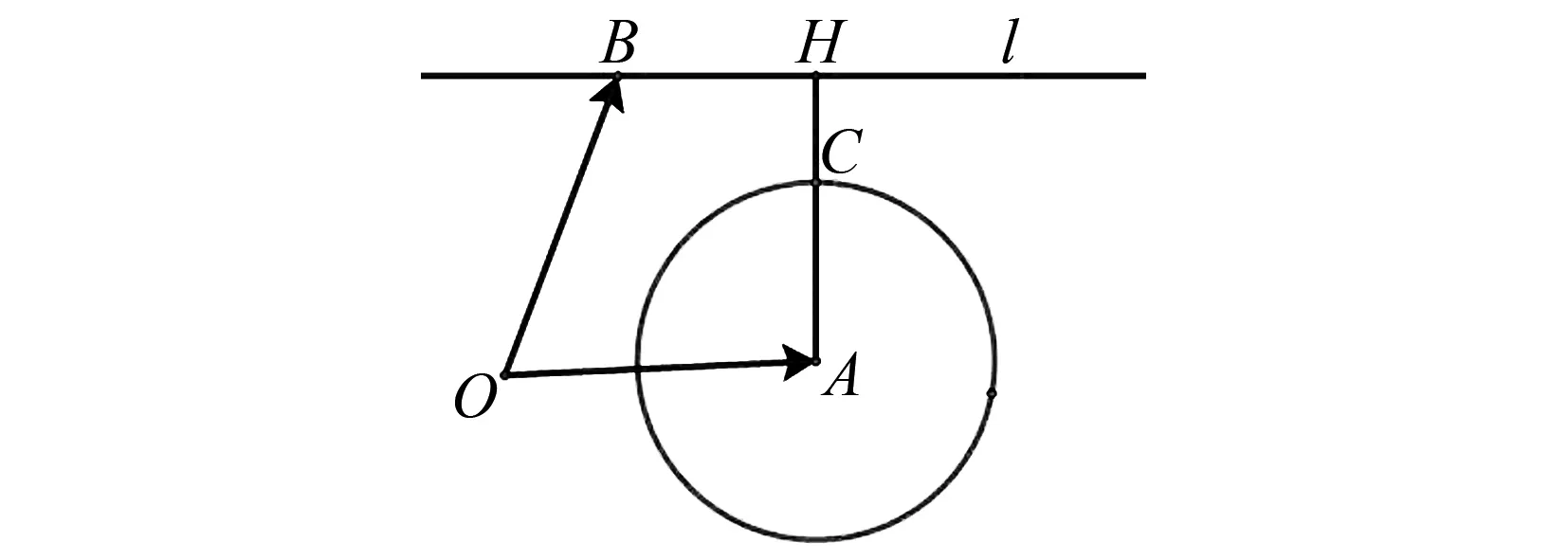
圖7 C軌跡為圓

點評根據|a|=2,把c2-2a·c+3=0轉為為c2-2a·c+a2=1,即(c-a)2=1,|c-a|=1,故點C位于以A為圓心,半徑為1的圓上,從而找出“隱圓”.

解決這類向量最值問題的策略就是利用坐標法或者幾何法得到動點的軌跡方程(即圓),再根據圓的幾何性質求出向量數量積的最值.