借助類比思維 破解數學解題困境

葉長春

(福建省永泰縣第一中學,福建 福州 350700)

類比思維是指對比兩個具有相似特征的事物,從某個已知事物中提取特征,并將該特征應用到另一事物推測中的思維活動.其本質是事物規律的遷移與應用.在數學解題中應用類比思維的優勢在于能降低學生思維難度,幫助學生迅速掌握某種規律與方法,突破各種題型的解題困境.

1 破解數列解題困境

數列習題的類型多變,解題方式靈活,只有找準解題方法才能迅速解題.但從實際來看,大部分學生并不具備這種能力.尤其是無法通過數列題型,聯想到倒序相加、消元等比較靈活的數列求解方式.所以,教師要啟發學生,引導學生探索掌握并遷移規律.

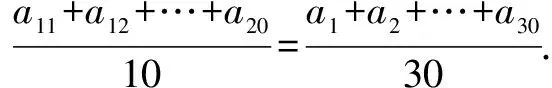
例1 已知數列{an}中,滿足a1=2,an+1=an+cn(c為常數,n=1,2,3…),且a1,a2,a3是公比不為1的等比數列.

(1)求c的值;

(2)求數列{an}的通項公式.

解析因為an+1=an+cn,所以得出an+1-an=cn,可以類比等差數列通項公式的推導方式.對于公差為d的等差數列,通項公式可以利用迭加法求解,即:當n≥2時,an-an-1=d,an-1-an-2=d,…,a3-a2=d,a2-a1=d,通過逐個相加可以得到:an=a1+(n-1)d.

(1)因為a1=2,所以a2=2+c,a3=2+3c,因為a1,a2,a3是等比數列,所以(2+c)2=2(2+3c),求解得出c=0或c=2.當c=0時,a1,a2,a3相等,不符合題意,舍去.當c=2時,a1=2,a2=4,a3=8,符合題意,所以c=2.

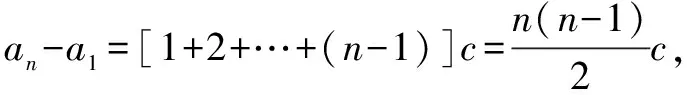
2 破解圓錐曲線解題困境

圓錐曲線包括橢圓、雙曲線、拋物線.雖然三種曲線形式表現不同,但是三者存在一定的共同點.比如具有類似的解析方程式、參數與性質等.從學生解題現狀來看,大部分學生經常混淆相似的基礎知識,且不懂得如何遷移與應用知識背后的數學規律,只能做到“依葫蘆畫瓢”,遇到新題目時仍然無從下手.所以,教師應當在解題教學中滲透類比思維,引導學生抓住知識本質,進行數學規律的遷移,提升學生的類比思維能力.

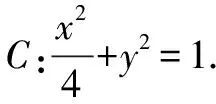
(1)過橢圓C右焦點作一條垂直于x軸的垂軸弦MN,求MN的長度.

(2)如圖1所示,若點P是橢圓C上不與頂點重合的任意一點,MN是橢圓C的短軸.直線MP、NP分別交x軸于點E(xE,0)和點F(xF,0),求xE·xF的值.

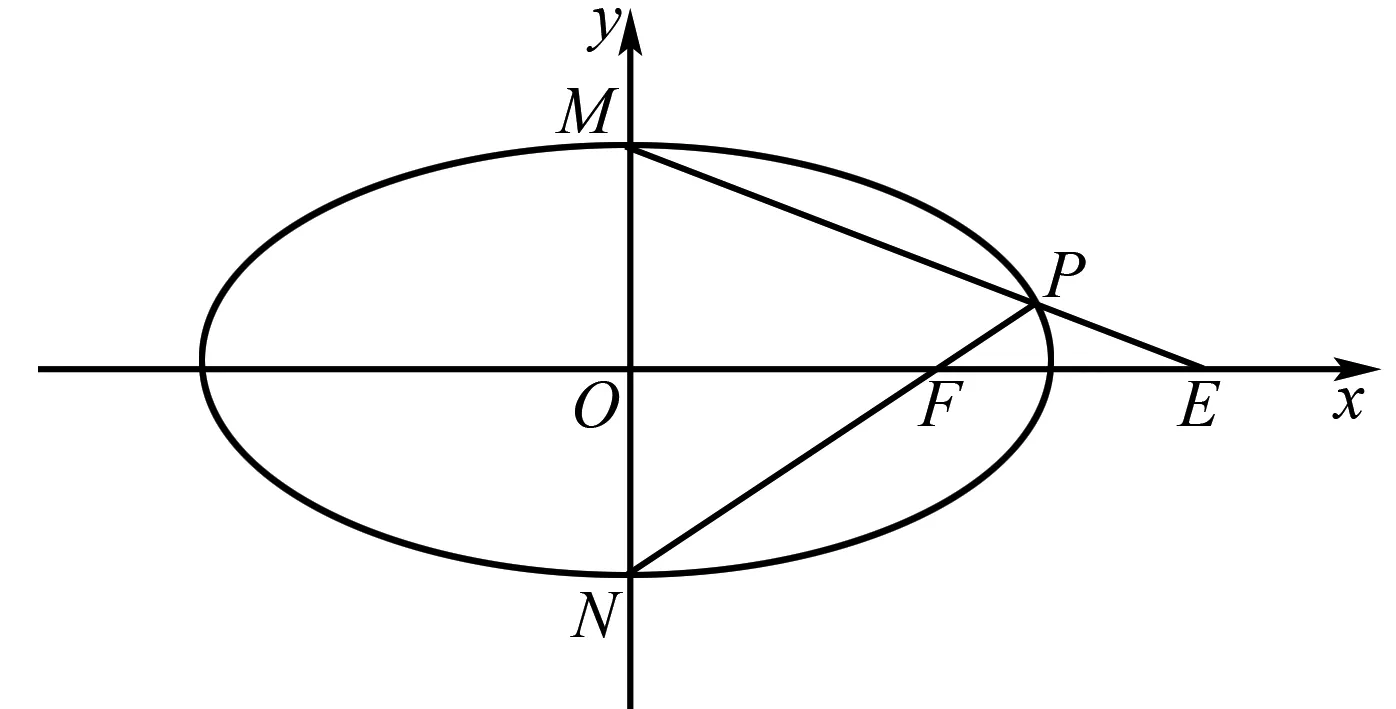
圖1 橢圓C示意圖

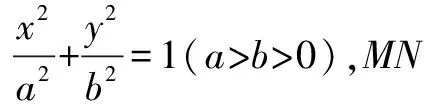
解析(1)|MN|=1(過程略).

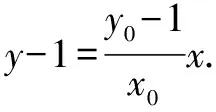
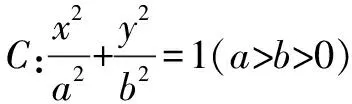
3 破解立體幾何解題困境

立體幾何是高考常見的知識點之一,其題型復雜、難度較高.部分學生會放棄立體幾何綜合題,導致成績不理想;還有部分學生只能完成綜合題中比較簡單的問題,而放棄難度較大的問題.針對這種情況,教師應積極改進解題方法,盡可能地發散學生思維,避免學生困于某個錯誤解題思路、某條錯誤輔助線的應用中,導致解題無法完成.

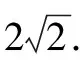
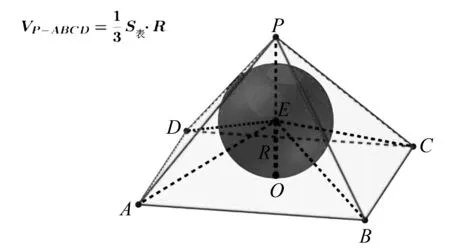
圖2 棱錐內切球體積示意圖

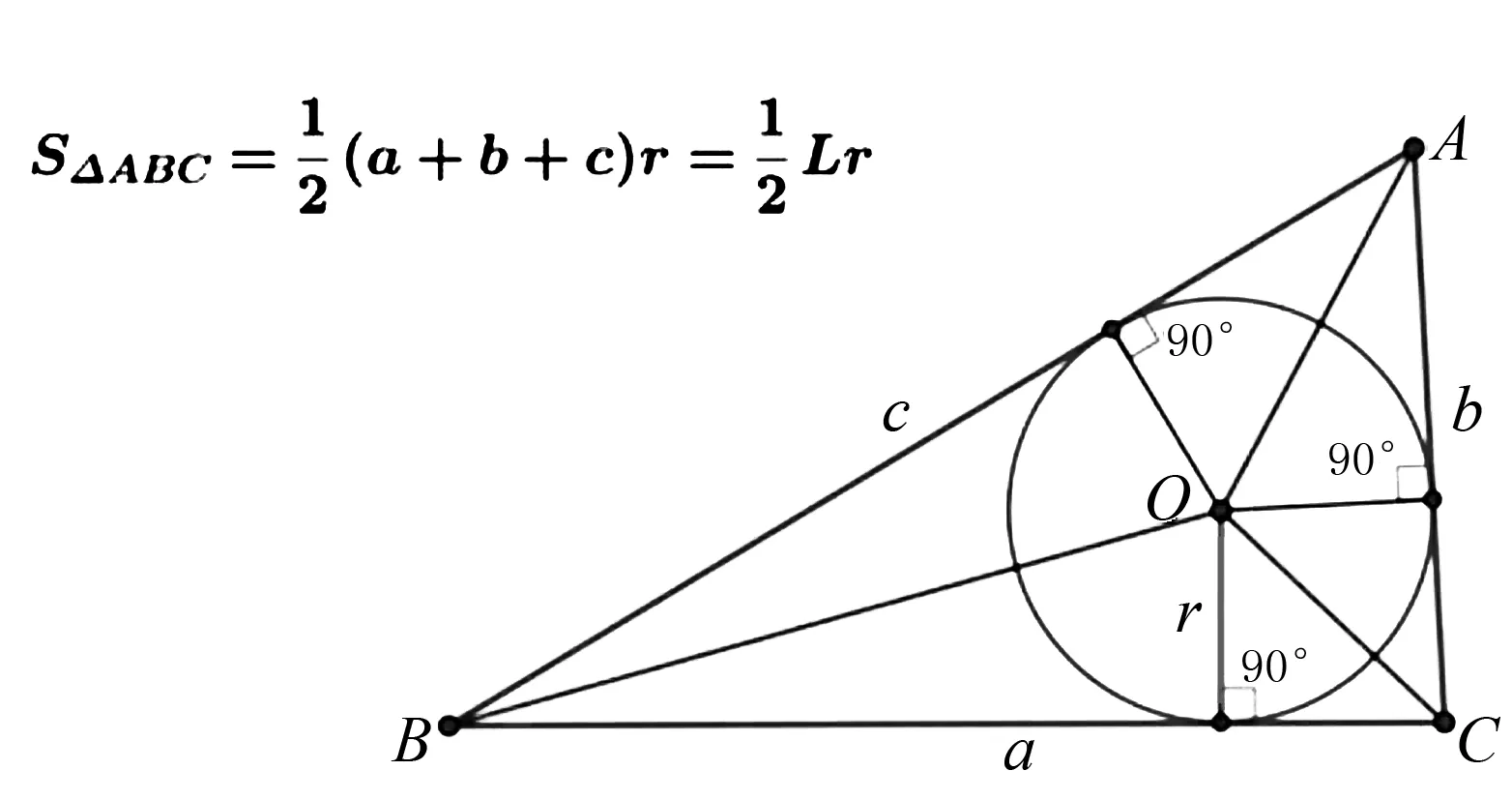
圖3 三角形內切圓面積示意圖

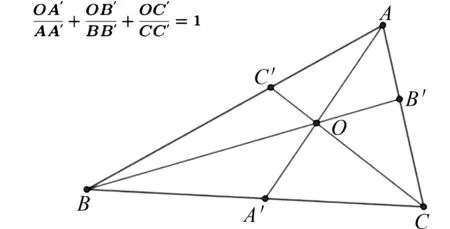
圖4 三角形示意圖

結合解題過程,類比三角形內切圓面積、棱錐內切球體積的解題思想不難發現,兩者擁有共同的解題思想即切割思想.將不易求解面積或體積切割成易求解的多個面積或體積.而且求解棱錐內切球體積所用的體積公式、面積公式均為學生熟悉的公式.可見,三角形內切圓面積求解思路為棱錐內切球體積求解指明了方向.

通過上述幾道例題的持續類比、推導,學生很快形成類比思維,而且也能鞏固記憶.通過上述類比推理推導出來的各種公式,再求解相似的立體幾何題目時會迅速確定解題思路,找到解題方法,從而突破以往思維困境,保證解題的順利進行[2].

總之,類比思想是一種不可忽視的數學思想,其在數學解題中應用非常廣泛.為了引導學生形成類比思維,突破各種解題困境,教師應當結合學生具體學情,將類比思想融入到解題教學中,并結合具體例題呈現類比思想應用方式.只有這樣才能持續強化學生的類比思維,使其不斷積累類比思維解題經驗,最終形成相應的解題能力.