高中數學解題中的數學思維能力的重要性

王曉豐

(江蘇省如東高級中學,江蘇 如東 226400)

數學思維能力作為學生認知數學內涵、提升數學學習效率的基礎能力,亦是其知識內化、思維躍遷的重要品質.對此,在實際教學中,高中數學應注重對學生數學思維能力的培養,加強各教學環節的聯動,充分發揮教材例題、生活案例等教育資源的優勢,保證學生課堂參與度的同時,提高他們的學習質量.基于此,本文將從以下幾個層面展開論述,以期為廣大學者后續研究提供價值借鑒.

1 數學思維能力內涵解讀

數學思維能力是指學生在學習活動中對知識解讀、知識運用、問題思考模式的綜合化體現,其涵蓋了學生邏輯思維、歸納概括、空間想象等能力[1].其中,邏輯思維能力能夠幫助學生快速梳理已有信息,并提煉知識、問題的核心思想;歸納概括能力則是學生問題分析、問題解決的重要前提,通過系統性、全面性的思考、分析,了解數學知識發展的一般規律,針對考查問題,制定具體的解決策略;空間想象則是學生數學建模意識培養的基礎能力,能夠幫助學生擺脫教材的束縛,通過聯想與總結,探尋在某一數學知識點在日常生活中的具體映射,進而準確掌握數學知識點或快速有效地解決問題.

2 數學思維能力于學生發展的現實意義

2.1 促進思維和能力的相互滲透

現階段高中學生正處于“形象思維”向“邏輯思維”過渡的關鍵時期,數學思維能力的介入,能夠幫助學生更好地理解抽象的數學知識,并結合自身認知建立相對完整的知識架構,形成獨有的思考模式[2].這種模式不僅能讓學生以高漲的學習熱情完成教師的既定任務,而且還能與其他學科建立有機聯系,促進學生多維度發展.

2.2 促進學生數學核心素養的個性化發展

隨著教育體系的不斷發展,核心素養成為當今教師教學工作的重要課題,加之社會經濟的不斷發展,社會對于人才能力、素養的需求愈來愈高,而這也使傳統的教學模式難以契合當今學生發展實際.新教育背景下,聚焦數學思維能力開展數學教學,能夠培養學生良好的自我總結、自我反思能力,同時以學生獨立思考、自主學習為主的教學工作能夠進一步深化學生認知思維,使其從多個角度綜合思考數學知識,并借助多種渠道進行思維內化,從而促進自身數學核心素養的個性化發展.

3 當下高中數學課堂教學工作現狀及成因

3.1 教學模式單一,學習熱情不高

受傳統應試教育思維的束縛,當前數學教學工作仍存在效率低、學生熱情不高等問題,究其原因在于教師教學方法過于局限,常根據教材知識點分布以及課程標準制定教學方案.在方式的選擇上,也以“知識講解+知識練習”的教學模式為主,并通過階段考試來分析學生知識掌握情況[3].這種教學模式雖然能夠保證教學進度與課堂教學質量,但方式的單一常常會影響學生學習熱情,加之課堂氛圍的枯燥,一些學生甚至出現消極、抵觸等心理,未深入理解高等數學的相關知識,也不能應用這些知識解決生活中的實際問題,限制了自身能力、思維的個性化發展.

3.2 教師缺乏深度教學思維,學生思維“固化”

目前來看,一部分教師未有意識地挖掘學生的數學思維,而將重心放到了課程的安排方面,著力于完成既定的教學任務,使學生有完美的成績.同時,還有一部分教師在評價時僅從其成績與課堂表現入手,根據其失分點,為其制定專項“題海”練習方案.這種指導方式雖然能夠讓學生記住知識點,但也極易讓他們陷入思維困境,即將知識套入固定的解題模板中,缺乏總結與反思.這種情況下,學生數學思維能力也難以得到有效提升.

4 高中數學解題中的數學思維能力培養具體策略

4.1 引入信息技術,提高空間想象能力

信息技術作為當今教師教學工作開展的重要輔助工具,其展現了良好的育人價值,一方面,教師可根據教學內容、課程標準為學生開發多元化的教學資源,縮短學生融入課堂的時間,保證教學工作的順利開展;另一方面,教師可借助信息技術將抽象的數學知識具體化,幫助學生理解的同時,提高其學習自信心與積極性[4].

立體幾何作為高中數學學習的難點之一,需要學生具備良好的空間想象能力與邏輯推理能力.因此,在實際教學中,教師可以借助信息技術搭建圖形與數字語言間的橋梁,以此來促進學生思維能力的提升,同時根據當下高中學生課堂參與度,設計相應的數學實踐活動,引導學生對數學知識進行觀察與思考,激起他們的學習興趣,促進其思維能力的養成.

例如,教師可設計如下例題:

在△ABC中,AB=3,AC=2,∠BAC=60°,M是BC的中點,N在直線AM上,且BN⊥AM、則向量在向量上的投影為多少?

首先,教師可讓學生梳理題目中現有信息,同時思考問題解決的具體方向.隨后教師可為學生準備相關的道具,鼓勵他們根據已有信息進行圖形制作,教師也可借助信息技術繪制圖形(如圖1),并與學生制作的圖形進行對比,以此幫助他們明確題目各信息的含義.

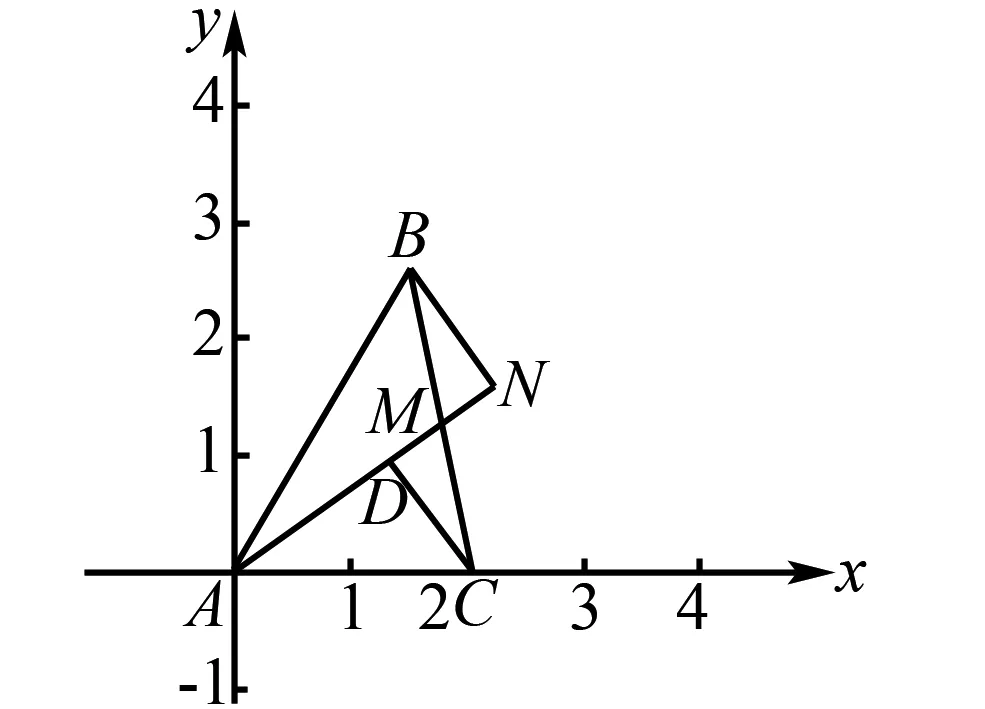
圖1 例題示意圖

在解決這類問題時,要逐步標注、分析各信息的含義,然后聯系已學知識尋找突破點.

根據題目現有信息,現以A為原點,AC為x軸,AC的垂線為y軸,建立平面直角坐標系,然后做輔助線CD垂直于AN.

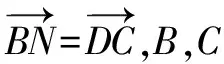
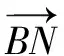
4.2 小組任務驅動,強化思維能力

小組合作是學生攻破學習難點的重要方式之一.對此,在實際教學中,教師同樣要利用小組合作模式開展教學工作,以“異質成組”為基本原則將班級內學生進行分組,使其呈現“以優帶弱,以思促質”的學習氛圍[5].同時,為了更好地培養學生數學思維能力,教師還可引入任務驅動教學法,根據教學內容設置多個子任務,引導學生進行階段思考,總結知識間的內在聯系,以此來推動其數學思維的綜合提升,對此,教師可設置如下例題:

在一塊長為4,寬為2的矩形紙板四角各截去一個邊長為a的正方形,然后將其折成一個沒有蓋的長方體.當a為何值時,長方體的容積最大,嘗試求Vmax.

該題函數式的構造過程比較簡單,但是包含著多個確定最值的思路.對此,教師可讓學生從不同方向思考最值確定的方法,以此來促使學生的思維能力得到充分有效的提升.

4.3 聯想思維培養,強化解題能力

聯想思維作為學生在數學學習中經常運用的思維,指的是兩知識點之間存有一定的聯系,并以此來互相展開聯想的一種數學思維方式.高中數學知識系統性較強,比如函數法則與幾何知識點之間就存在著很多共通之處,二者之間存在著緊密聯系關系,學生在面對其中某一知識點時就可以建立起聯想思維.教師應當積極指引學生去觀察各知識點之間的聯系,精準把握其中的內在聯系,進而鍛煉學生多方面思考與處理數學問題的能力,推動其數學思維能力得到有力地提升[6].

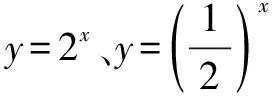
綜上所述,聚焦高效課堂建設,提高學生數學思維能力已成為教師教學工作開展的首要目標.在實際教學過程中,教師應深入解讀數學學科與學生能力、素養發展間的內在聯系,改變傳統“知識主導”的教學架構,加強教學資源與教學服務的開發與運用,創設趣味性、實效性兼備的課堂環境,提升課堂溫度,點燃學生學習熱情,從而加快落實核心素養培育工作的根本任務.