多因素約束下公路橋涵裝配式構件生產車間工期優化模型及應用*

李佳希 于競宇 陳川輝 王波

(合肥工業大學土木與水利工程學院，安徽 合肥 230009)

0 引言

2020年，住房和城鄉建設部、國家發展和改革委員會等部委聯合印發《關于推動智能建造與建筑工業化協同發展的指導意見》(建市〔2020〕60號)，提出推動建筑工業化、數字化和智能化升級，助推建筑業高質量發展。2021年，中共中央、國務院印發《國家綜合立體交通網規劃綱要》，提出到2035年，國家綜合立體交通網實體線網總規模合計70萬km左右(不含國際陸路通道境外段、空中及海上航路、郵路里程)。在加快建設交通強國、構建現代化高質量綜合立體交通網的背景下，公路橋涵建設面臨新的要求。

在國家相關政策推動下，裝配式建筑得到快速發展。與傳統公路橋涵構件生產模式相比，公路橋涵裝配式構件所有生產工序均在室內車間進行，可確保預制構件各道工序全天候、不間斷生產，不受大風、降雨、冰凍等不利自然氣候條件影響，有效提高了公路橋涵裝配式構件產能。同時，公路橋涵裝配式構件預制生產質量更加可控[1]。公路橋梁大型裝配式構件生產屬于典型的混合流水車間調度問題(Hybrid Flow Shop Scheduling Problem，HFSP)，可以描述為：在生產流水線上對N個獨立的構件進行生產，該生產系統中的每一個構件都有I道工序，每一道工序都有J臺設備，且每一個需要生產的構件中至少有一道工序需要多臺并行機，設備使用情況符合占用約束和順序約束。

公路橋涵裝配式構件體積大、生產車間內部空間受限，同時需要滿足公路項目建設施工需求，因此生產工期較緊。目前，公路橋涵裝配式構件的生產過程中人工投入大、生產效率低，且車間內存在生產缺乏規劃、布局不合理等問題。為了進一步優化生產工期，提高車間內的生產效率，本文提出一種多因素約束下公路橋涵裝配式構件生產車間工期優化模型。

1 文獻綜述

近年來，隨著裝配式構件的快速發展，裝配式構件的生產調度問題得到業界學者關注。龍春曉[2]從預制構件生產流程入手，對生產工序進行劃分，并根據實際數據求出每項工序的學習曲線方程，結合生產過程的其他限制條件，建立適用于預制構件生產過程的人力配置方案；謝思聰等[3]在對比分析預制構件生產與一般制造業區別的基礎上，提出預制構件廠生產參數的量化途徑，采用基于多層編碼遺傳算法解決預制構件的生產調度優化問題；李瑩瑩[4]指出，目前我國裝配式建筑發展仍處于探索階段，規模化、標準化、工業化、通用化、產業化水平不高，初期投資成本較大，諸多原因導致裝配式工業化建筑成本偏高；Mahdavi等[5]通過工人資源的分配優化，實現了對工人資源的多目標優化調度研究；Ko等[6]以最短完工時間和延誤或提前交貨懲罰成本為目標，構建多目標預制構件生產調度模型；Yang等[7]以完工時間、合同罰款、工作站空閑時間最短等為目標，構建多條預制生產線的生產調度模型；Wang等[8]考慮了模具制造、運輸過程等對預制構件生產的影響，以最小化拖延和提前處罰的總成本為目標，構建了改進的預制構件生產調度模型；Ma等[9]提出了預 制 生 產 線 流 水 作 業 調 度 模 型(MP-FSM)和基于遺傳算法的流水作業調度優化方法，實現了多生產線流水作業調度的優化；趙芮等[10]以最小化最大完工時間和最小化最大拖期為目標，提出了一種多目標離散正弦優化算法方法。

由此可見，對于車間調度優化問題的求解，智能優化算法是最主要的手段，也是當前生產調度領域的研究熱點。目前，車間生產線調度使用較多的求解算法有遺傳算法、蟻群搜索算法、模擬退火算法、粒子群算法等。遺傳算法應用領域廣泛，具有群體搜索的特點，適用于復雜大型的非線性問題，但容易出現過早收斂的問題，且效率不高；蟻群搜索算法全局搜索能力強但局部搜索能力較弱，往往只能得到次優解；模擬退火算法全局尋優能力強但效率不高；粒子群算法搜索速度快，但極易陷入局部最優；正余弦優化算法具有高度的靈活性，原理簡單，易于實現。

在裝配式構件生產和調度問題相關研究中，研究對象大多是體積/質量小、生產工序復雜的小型裝配式構件，對于大型裝配式構件的研究集中于構件結構設計、建造技術、質量管理等方面。王彬等[11]提出了裝配式構件的新工法；史宏剛等[12]結合實際問題，為提升構件生產質量提供技術保障。基于此，本文考慮多種約束因素，如受季節因素影響的生產時長和受工作時間約束的工人影響，利用正余弦算法建立一種適用于公路橋涵大型裝配式構件的生產車間工期優化模型，并在實例中進行驗證，通過借助收斂速度較快且具有高探索性和局部最優避免性的正余弦算法求解，達到工期最優化的目的。

2 公路橋涵裝配式構件生產車間工期優化模型構建

2.1 模型描述

作為典型的HFSP問題，公路橋涵裝配式構件生產車間優化可描述為：數量為N的構件需要在I段工序J條生產線上完成生產，每段工序上有J個生產工位，每個構件的生產順序相同。調度目標為：N個構件生產的最短工期。

與傳統問題不同的是，公路橋涵裝配式構件體積大、影響因素多，具有一定的特殊性，因此，生產時需要考慮多種因素。本文考慮受工作時間約束的工人和受季節因素影響生產時長的工段，以此為每個構件的每段工序確定最佳生產工位，進而提高確定N個構件生產最短工期的準確性。模型符號和變量定義見表1。

表1 模型符號和變量定義表

同時，根據生產要求做出以下假設：

(1)在所有工序開始前，工人和機器準備就緒，不考慮準備工作時間。

(2)不考慮構件加工過程中工序之間的運輸轉移時間。

(3)不考慮機械故障。

(4)不考慮生產過程中出現質量問題導致的重新加工。

(5)車間內構件的生產工序一開始已確定。

2.2 模型構建

分析受工作時間約束的工人和受季節因素影響生產時長的工段，建立以生產工期為優化目標的車間調度優化模型，即

Obj.MIN(TN)=MIN(max(tfijn)1≤j≤J，1≤i≤I-
min(tsij11)1≤j≤J，1≤i≤I)

(1)

s.t.

max(Y，Z)≥6l，min(Y，Z)≥4+2bJ

(2)

ts(i+1)n>tfin

(3)

tijk=w×tij

(4)

Ht≤Hmax，Hmax=(max(Y，Z)-6l)×J/l

(5)

式(1)表示目標函數生產工期最小化；MIN表示最小值函數；min表示最早時間值；max表示最晚時間值；max(tfijn)1≤j≤J，1≤i≤I表示最后一個進行第I個工序的公路橋涵裝配式構件完成第I個工序加工的自然時間；min(tsij11)1≤j≤J，1≤i≤I表示最早一個進行第一個工序的公路橋涵裝配式構件開始第一個工序加工的自然時間。

式(2)表示車間場地面積約束，根據車間場地面積和待生產裝配式構件的長度寬度確定生產線J的總條數；式(3)表示工序時間約束，其中，ts(i+1)n表示第n個待生產裝配式構件在任一生產線上開始加工第i+1個工序的自然時間，tfin表示第n個待生產裝配式構件在任一生產線上完成加工第i個工序的自然時間；式(4)表示受季節因素影響的生產時長，其中，tij表示第j條生產線第i段工序的基準時間，基準時間為工序在設定的生產環境下加工時間，tijk表示當前生產環境下第j條生產線第i段工序上加工第k個T梁的預測時間，w表示生產環境對基準時間的影響系數，w為經驗值，一般春秋季取值為1，夏季取值為0.7～0.9，冬季取值為1.1～1.3；式(5)表示堆積約束，即生產過程中可在裝配式構件生產車間內短暫堆積未加工完成的構件約束，其中，Ht表示t時刻裝配式構件生產車間內短暫堆積未加工完成的構件數量，Hmax表示T梁車間內允許最大堆積的未加工完成構件數量。

3 正余弦算法

3.1 算法簡介

正余弦優化算法(Sine Cosine Algorithm，SCA)是一種新型智能優化算法。在算法中會生成多個初始隨機候選解，并使它們基于正弦和余弦的數學模型向外波動或向最優解的方向波動，利用多個隨機變量和自適應變量來計算當前解所在位置，從而可以搜索空間中的不同區域，有效地避免局部最優，收斂于全局最優。

正余弦優化算法具有高度的靈活性，原理簡單，易于實現，適用于不同領域的優化問題。正余弦優化算法的尋優過程可分為兩個階段：在探索階段，優化算法通過結合某隨機解在所有隨機解中快速尋找搜索空間中的可行區域；在開發階段，隨機解會逐漸發生變化，且隨機解的變化速度會低于探索階段的速度。在正弦余弦算法中，候選解會被隨機初始化，再根據正弦或者余弦函數并結合隨機因子來更新當前解在每一維度上的值。

3.2 編碼方案與初始化

3.3 參數設置

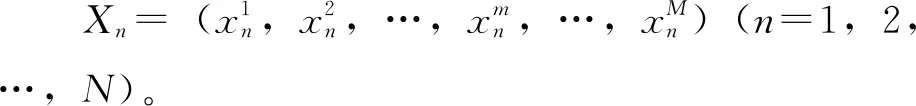
第t+1次迭代時個體第m維位置分量的更新為

r1=a×(1-t/tmax)

(7)

在式(7)中，tmax為最大迭代次數；a為常數，一般取值為2。

3.4 算法求解流程

使用正余弦算法求解多因素約束下公路橋涵裝配式構件生產車間最短工期，算法流程圖如圖1所示。

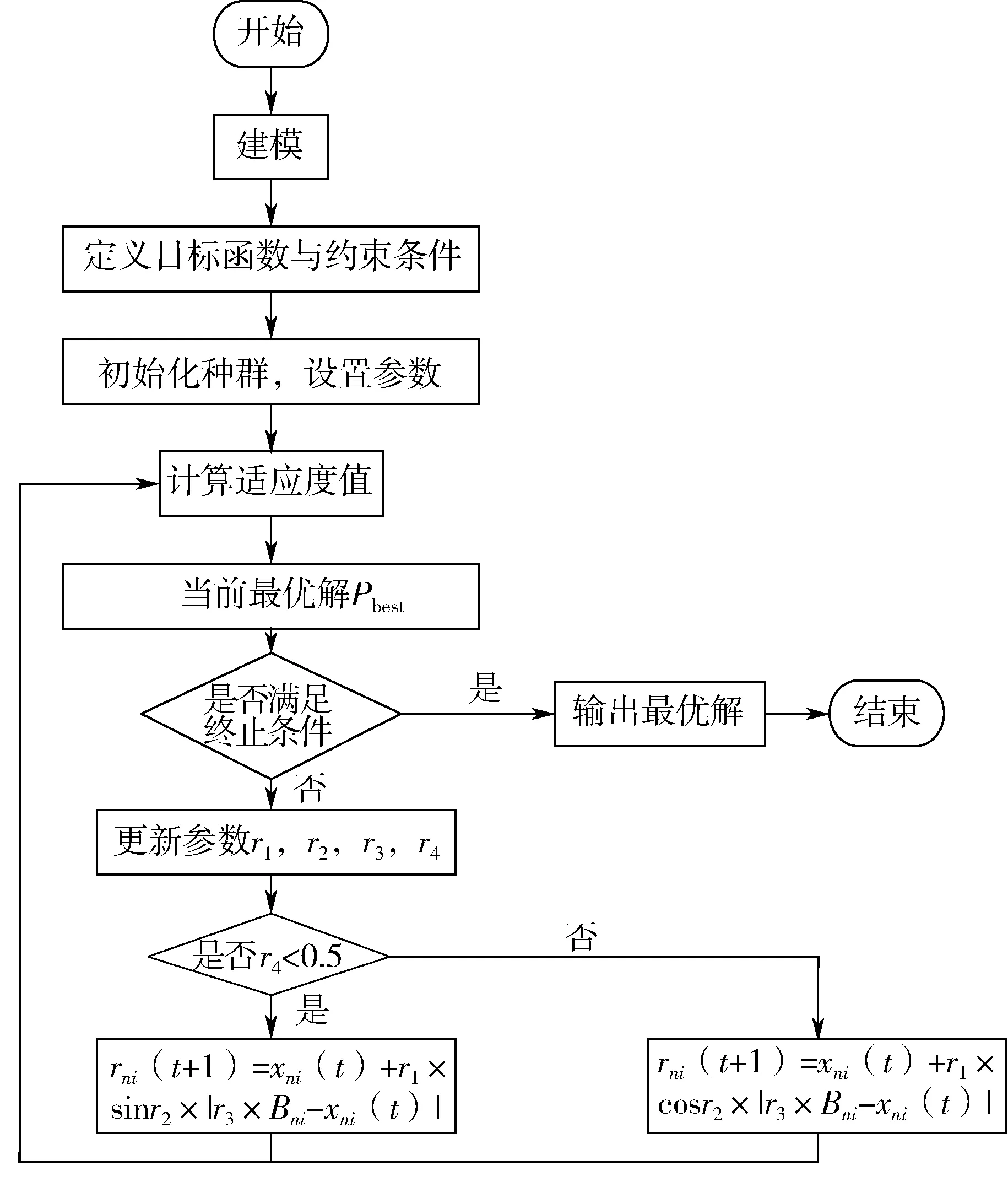
圖1 正余弦算法求解最短工期流程圖

具體步驟如下：

(1)建立構件生產車間受多因素約束的數學優化模型，將最短工期定義為優化模型的目標函數，確定決策變量和約束條件。

(2)定義求解構件生產車間最短工期中采用基于工件排序的自然數編碼。

(3)種群初始化。初始種群隨機產生，隨機的初始種群更有可能在迭代之初遍布可行域的搜索空間，提高算法的多樣性。

(4)設置r1、r2、r3、r44個參數，r1由式(7)決定，r2是[0，2π]之間的隨機數，r3是[0，1]之間的隨機數，r4也是[0，1]之間的隨機數。

(5)根據式(6)計算當前適應度值和當前最優解Pbest。若不滿足終止條件，則執行步驟4，進入迭代循環。反之，輸出最優解，結束迭代。

4 案例分析

4.1 案例簡介

本文以D梁廠為例進行分析。D梁廠施工區域分為輕型T梁預制區、箱涵拱涵預制區、圓管涵蓋梁預制區、鋼筋加工場，預制總砼方量為14.25萬m3。T梁車間面積為124m×54m；車間內工人工作時間為8：00～12：00，14：00～18：00，單休。該車間主要生產的公路橋梁大型裝配式構件為25m輕型T梁，臺座尺寸為100cm×1504cm×2490cm。原計劃采用固定模臺生產線布局形式，生產線采用移動臺座+固定液壓模板的形式，模板采用底模移動，側模固定方式，每條生產線配備1套液壓模板，4個移動臺座，生產線分為鋼筋綁扎工位、混凝土澆筑工位、蒸養工位、張拉壓漿工位。工序如下：

(1)鋼筋綁扎。可間斷，必須在工作時間段開始，也必須在工作時間段完成。一片T梁在該工序生產時間t1=24/人數(h)。

(2)混凝土澆筑。不可間斷，必須在工作時間段開始并在同一工作時間段完成。一片T梁在該工序生產時間t2=1.5h。

(3)脫模。混凝土澆筑結束立即開始計算脫模時間，可在任意時間段完成。現取一片T梁在該工序生產時間t3=10w3。w3為季節系數，春秋w=1；夏季w=0.8；冬季w=1.2。

(4)蒸養。必須在工作時間段開始，可在任意時間段完成。現取一片T梁在該工序生產時間t4=24w4。w4為季節系數，春秋w=1；夏季w=0.9；冬季w=1.1。

(5)張拉壓漿。不可間斷，必須在工作時間段開始并在同一工作時間段完成。一片T梁在該工序生產時間t5=1h。

4.2 仿真分析

正余弦算法的參數設置如下：種群規模為1920，最大迭代次數為100。正余弦算法收斂曲線如圖2所示，調度甘特圖如圖3所示。

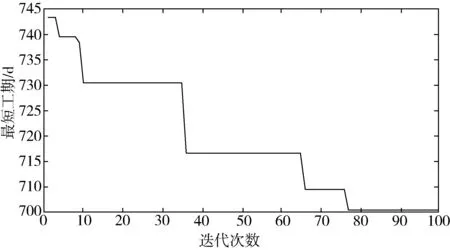
圖2 正余弦算法收斂曲線

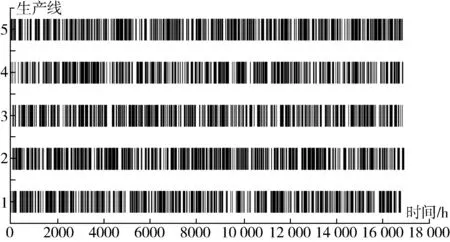
圖3 調度甘特圖

4.3 結果分析

通過優化前后的對比結果(表2)可知，工期縮短38d，人工量減少760工日。本次優化嚴格按照工人工作日歷安排生產工作，考慮工序受各生產因素影響，盡可能地優化了最短工期，有效減少了人工成本。通過對此次優化進行詳細分析可知，工期優化主要集中在鋼筋綁扎和混凝土澆筑兩個工序。通過合理安排工人數量對各工序做出最優調度安排。

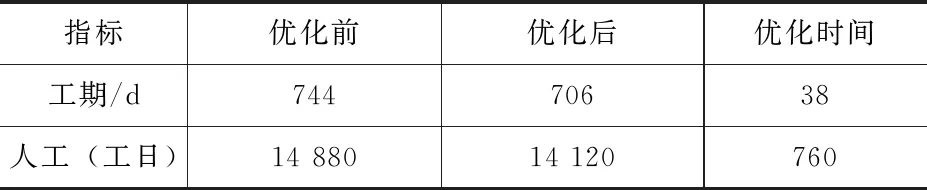
表2 優化前后對比結果

5 結語

本文在考慮公路橋涵裝配式構件生產時間受工人的工作日歷影響和生產工序時長受季節因素影響的基礎上，構建針對公路橋涵裝配式構件生產車間工期優化模型，并使用實際算例進行驗證。通過該模型使用正余弦算法求出算例中車間內生產任務的最短工期，并對車間內各待生產構件的工序做出最優調度安排。實驗結果表明，該方法優化了最短工期，有效減少了人力和生產成本。同時，正余弦算法收斂速度快，適用于裝配式構件生產研究，可為其他類似預制構件生產的調度安排提供參考。