問渠哪得清如許,為有源頭活水來
——談抽象函數中的單調性應用技巧
■樂和順
抽象函數通常是指沒有給出具體的函數解析式,只給出了其他一些條件(如函數的定義域、經過的特殊點、解析遞推式、部分圖像性質等)的函數。抽象函數是高中數學的難點,也是高中與大學的一個知識銜接點。因為抽象函數沒有具體的解析式,所以判斷或應用其單調性時就比較困難。下面就幾類常見的抽象函數的單調性的應用技巧,進行實例剖析。
一、單調性定義的巧妙應用
根據函數單調性的定義,函數單調性判斷的“三部曲”:任給定義域內的兩個值x1,x2,并規定它們的大小;比較兩處函數值的大小(常規方法是作差);根據定義產生結論。
例1 已知定義在R 上的函數f(x),對任意實數x、y,恒有f(x)+f(y)=f(x+y),且當x>0 時,f(x)<0。求證:函數f(x)在R 上是減函數。
分析:利用函數單調性的定義,按照三個步驟進行分析與證明。
證明:設x1,x2∈R,且x1>x2,則x1-x2>0。
由已知條件知,當x>0時,f(x)<0,所以f(x1-x2)<0。
因為f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)+f(x2)-f(x2)=f(x1-x2)<0,所以f(x1) 抽象函數的單調性問題,可通過抽象函數的分析,結合函數單調性的定義求解。解決抽象函數的單調性問題的關鍵是把x1寫成,或把x1寫成(x1-x2)+x2的形式進行變形分析與處理。 變形練習1:已知f(x)是定義在(0,+∞)上的函數,且當x>1時,f(x)>0。對于一切實數x,y都有f(xy)=f(x)+f(y),求證:函數f(x)在(0,+∞)上是增函數。 函數的單調性與奇偶性是函數的兩個重要性質,它們之間相輔相成,又有區別與聯系,利用函數的單調性與奇偶性,可以巧妙地處理一些相關的抽象函數問題。 分析:根據函數的單調性的定義,結合奇函數的性質加以判斷。注意利用單調性的定義時,x1,x2的取值要結合對應的區間加以選取。 任取x1,x2∈(-∞,0),且x1 因為y=f(x)在(0,+∞)上是增函數,且f(x)<0,所以f(-x2) 因為y=f(x)是奇函數,所以f(-x2)=-f(x2),f(-x1)=-f(x1),所以f(x2) 本題容易出現的錯誤是:在區間(0,+∞)上任取x1,x2且x1 變形練習2:已知函數f(x)是R 上的奇函數,且在(0,+∞)上是增函數,證明函數f(x)在(-∞,0)上也是增函數。 提示:任取x1,x2∈(-∞,0),且x1 因為f(x)是R 上的奇函數,所以 f(-x1)=-f(x1),f(-x2)=-f(x2)。① 由f(x)在(0,+∞)上是增函數,可得 f(-x1)>f(-x2)。 ② 把①代入②得f(x1) 函數的單調性是函數的重要性質之一,函數的單調性在比較大小、求函數的值與最值,以及求參數問題都有廣泛的應用。 分析:抽象函數在特定區間上的最值問題,要根據其相應區間的單調性加以分析與求解。本題中只給出x>0時的情況,這時要結合已知條件,先判斷函數的奇偶性,再求出最值。 令x=y=0,則f(0)=0。令y=-x,則f(x)+f(-x)=f(0)=0,即f(x)=-f(-x),所以函數f(x)為奇函數。 對任意x1,x2∈R,且x1 因為f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)<0,所以f(x1) 因為f(3)=f(2+1)=f(2)+f(1)=3f(1)=-2,所以f(-3)=-f(3)=2,所以函數f(x)在區間[-3,3]上的取值范圍為[-2,2],所以函數f(x)在區間[-3,3]上的最大值為2,最小值為-2。 抽象函數在單調區間上的最值問題,可利用函數單調性的定義,結合函數的奇偶性加以解決。 變形練習3:已知函數y=f(x)在區間(-1,1)上是減函數,且f(1-a)-f(2-3a)>0成立,求實數a的取值范圍。 提示:由f(1-a)-f(2-3a)>0,可得f(1-a)>f(2-3a)。

二、結合奇偶性的應用
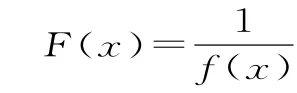

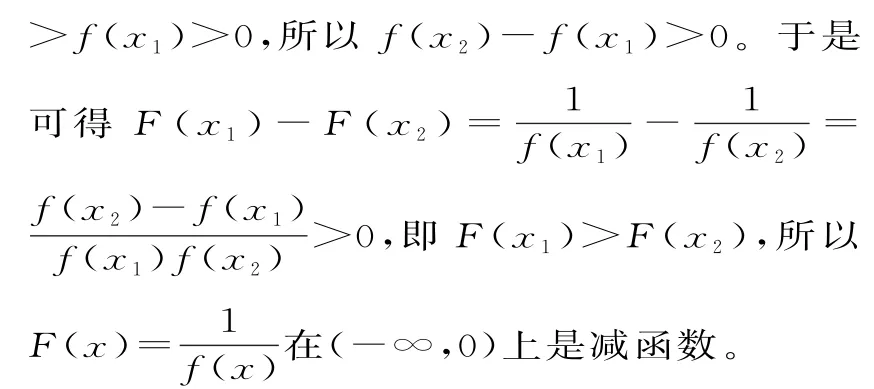
三、實際問題的創新應用







