學透函數的奇偶性
2023-10-28 09:02:04韓雨彤
中學生數理化·高一版 2023年10期
■韓雨彤
函數的奇偶性是函數的主要性質之一,它常和函數的單調性、對稱性、周期性交匯命題,且是每年高考的常考點。
一、函數的奇偶性
例1 已知定義域為[1-2a,a+1]的奇函數f(x)=x3+(b-1)x2+x,則a+b=____。
解:由題意得1-2a+a+1=0,所以a=2。因為函數f(x)是奇函數,所以f(-x)=-f(x),即-x3+(b-1)x2-x=-x3-(b-1)x2-x,所以(b-1)x2=0恒成立,所以b-1=0,即b=1。故a+b=3。

函數具有奇偶性的必要條件是定義域關于原點對稱,在此條件下,若f(-x)=-f(x),則函數f(x)為奇函數;若f(-x)=f(x),則函數f(x)為偶函數。反之亦然。
二、函數的奇偶性與對稱性
例2 已知函數f(x)=ax5+bx3+3且f(2023)=16,則f(-2023)的值為_____。
解:令g(x)=ax5+bx3。因為f(x)=ax5+bx3+3,所以f(x)=g(x)+3。
因為g(x)是奇函數,所以函數g(x)的圖像關于原點(0,0)對稱,所以g(-x)+g(x)=0。
因為f(-x)+f(x)=g(-x)+g(x)+6=6,所以f(-2023)+f(2023)=6。
又f(2023)=16,所以f(-2023)=6-16=-10。

奇偶性只是對稱性的一種特殊情況。奇函數的圖像關于原點對稱,偶函數的圖像關于y軸對稱。
三、函數的奇偶性與周期性

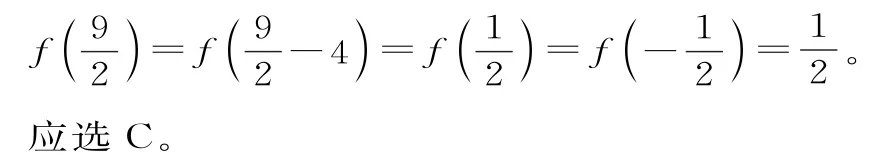

先利用函數的奇偶性,求出函數的周期,再適當賦值,即可求出函數的值。
四、函數的奇偶性與單調性

先由已知條件得到g(x)在R 上為單調遞減函數,由g(x)為奇函數得到g(m)>g(2-m),再結合函數的單調性即可求得m的取值范圍。

