如何解答函數單調性的熱點問題
■孫海燕
函數的單調性是函數的重要性質,解答函數問題,離不開函數的單調性的應用。下面就函數單調性的熱點問題進行舉例分析,供大家學習與參考。
一、求函數的單調區間
求函數單調區間的兩種方法:一是利用基本初等函數的單調性;二是利用函數的圖像,觀察增減區間。求單調區間時,不連續的單調區間必須分開寫,不能用“∪”符號連接;求函數的單調區間不能忽略函數的定義域,單調區間應是定義域的子集。
例1 求下列函數的單調區間,并指出該函數在其單調區間上是增函數還是減函數。
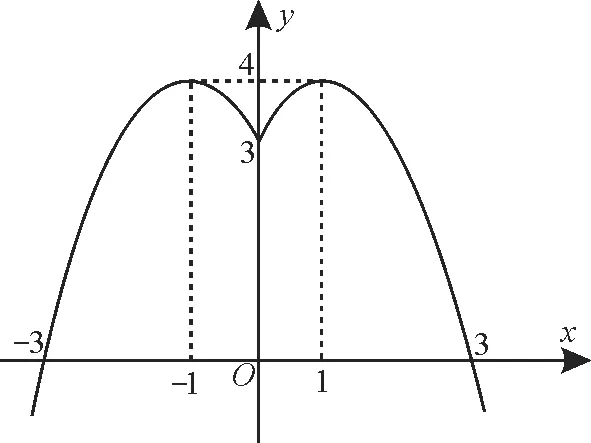
圖1

由圖可知,此函數在(-∞,-1],[0,1]上單調遞增,在[-1,0],[1,+∞)上單調遞減。
評析:一次函數的單調性看一次項系數的正負就可以判斷;含有絕對值的函數,可先根據絕對值的意義,將其轉化為分段函數,再結合圖像即可確定單調區間及單調性。
二、利用函數的單調性求參數的取值范圍
函數單調性應用的關注點:函數單調性的定義具有“雙向性”,利用函數單調性的定義可以判斷或證明函數的單調性,反過來,若已知函數的單調性,可以確定參數的取值范圍。利用函數的單調性可以比較函數值或自變量的大小。若一個函數在區間[a,b]上是單調的,則此函數在區間[a,b]內的任意子集上也是單調的。上單調遞增,畫出此函數的大致圖像,如圖2所示。由圖可知,需滿足g(1)≤h(1),即a-3≤3,所以a≤6。
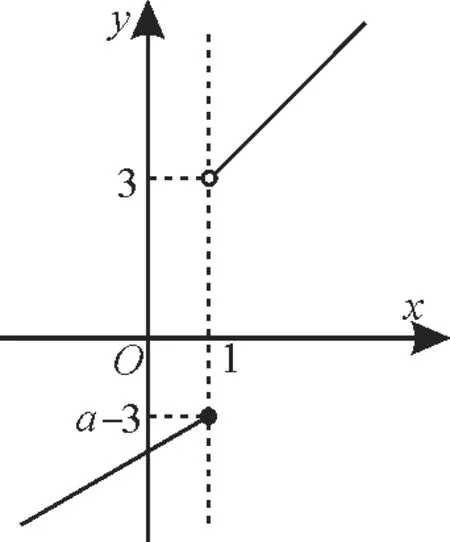
圖2

綜上可得,實數a的取值范圍是2 評析:利用函數的單調性,求含參數的分段函數應抓住兩點:一是嚴格遵循函數單調性的定義;二是結合函數圖像求出參數的限制條件,也就是關于參數的不等式。 利用函數的單調性解不等式,一定要注意函數的定義域,也就是要先考慮函數的定義域,否則容易出現錯解。 例3 已知函數f(x)是增函數,定義域為(0,+∞),且f(4)=2,f(xy)=f(x)+f(y),求滿足f(x)+f(x-3)≤2的x取值范圍。 因為f(x)+f(x-3)≤2,又f(xy)=f(x)+f(y),所以f[x(x-3)]=f(x)+f(x-3)≤2=f(4)。 又因為f(x)在(0,+∞)上是增函數,所以x(x-3)≤4。 評析:函數的單調性是相對于函數定義域內某個子區間而言的“局部”性質,它反映了函數在某個區間上函數值的變化趨勢。在利用函數的單調性解決問題(本題是利用函數的單調性解不等式)時,如果不考慮函數的定義域盲目解題,就會造成錯解。 同學們可以看看該題以下的解題過程,想必會從中有所領會: 錯解:因為f(x)+f(x-3)≤2,且f(xy)=f(x)+f(y),所以f[x(x-3)]=f(x)+f(x-3)≤2=f(4)。又因為f(x)在(0,+∞)上是增函數,所以x(x-3)≤4,解得-1≤x≤4,即所求x的取值范圍是-1≤x≤4。 錯解忽視了函數的定義域為(0,+∞)這一隱含條件,若f(x)+f(x-3)=f[x(x-3)],則x>0,x-3>0,且x(x-3)>0,在此條件下再去解不等式,才是正確的思路。三、利用函數的單調性解不等式


四、利用函數的單調性求函數的最值


