既要重視“形”,也要關注“數”
——談冪函數中的應用問題
■任 遠
冪函數是重要的基本初等函數之一。熟練掌握冪函數的概念、圖像與性質是解決冪函數問題的關鍵。下面結合實例對冪函數的常見題型加以展示,希望對同學們的學習有所幫助。
一、冪函數的概念問題
判斷一個函數是否為冪函數,要掌握冪函數的概念,確定其系數為1,不含常數項,指數是常數,底數只能為自變量x,而不能是x的函數。
例1 若函數f(x)=(m2-4m-4)xm是冪函數,則m=_____。
分析:抓住冪函數的概念,借助系數為1建立含有相應參數的方程,通過解方程來確定相應的參數值。
解:因為函數f(x)是冪函數,所以m2-4m-4=1,即m2-4m-5=0,解得m=5或m=-1。答案為5或-1。

一個函數為冪函數的依據是該函數為y=xα(α為常數)的形式,同時滿足三個條件:指數為常數,底數為自變量,xα系數為1。如函數y=(3x)α,y=2xα,y=xα+5都不是冪函數。
二、冪函數的圖像及應用問題
要熟練掌握冪指數在α>1、α=1、0<α<1、α=0,以及α<0 情況下冪函數y=xα的圖像特征,由此可以判斷對應的函數圖像和簡單的應用問題。
例2 圖1是冪函數y=xm與y=xn在第一象限內的圖像,則( )。

圖1
A.-1 B.n<-1,0 C.-1 D.n<-1,m>1 分析:先利用冪函數y=xα(α為常數)在第一象限內的圖像變化規律,結合區間(0,1)內的取值進行比較,再判斷對應冪指數的參數的取值情況。 解:(方法1)由圖知,y=xm在[0,+∞)上是增函數,y=xn在(0,+∞)上是減函數,所以m>0,n<0。又當x>1 時,y=xm的圖像在y=x的下方,y=xn的圖像在y=x-1的下方,所以m<1,n<-1。綜上可知,0 (方法2)在區間(0,1)內作直線x=x0,與兩個圖像都有交點(作法略)。根據“點低指數大”的圖像特征,可得0 依據圖像高低判斷冪指數大小的相關結論:在區間(0,1)內,冪指數越大,冪函數的圖像越靠近x軸(簡記為“指大圖低”);在區間(1,+∞)內,冪指數越大,冪函數的圖像越遠離x軸(簡記為“指大圖高”)。由圖像確定冪指數α與0,1的大小關系,可根據冪函數在第一象限內的圖像(類似于y=x-1,y=或y=x3等)來判斷。 借助冪指數的相關取值情況及所對應的冪函數的單調性,可判斷相關代數式的大小關系。 例3 比較下列各組數中兩個數的大小關系。 比較冪值大小的兩種常用的基本方法:直接法,當冪指數相同時,利用冪函數的單調性進行比較;轉化法,當冪指數不相同時,先轉化為相同的冪指數,再利用單調性進行比較。 對于冪函數的綜合應用問題,可利用相應的數學知識與相關的數學思維,結合冪函數的性質進行分析與處理。 例4 已知冪函數f(x)=x-k2+k+2(k∈Z)在區間(0,+∞)上為增函數。 (1)求整數k的值。 分析:利用冪函數在區間(0,+∞)上為增函數,確定冪指數α>0,結合二次不等式的求解和參數k∈Z,確定整數k的值;由冪函數f(x)的解析式,得到函數g(x)的解析式,通過配方法處理,再結合分類討論確定正數p的存在情況。 解:(1)由冪函數f(x)在區間(0,+∞)上為增函數,可得-k2+k+2>0,即k2-k-2<0,解得-1 冪函數y=xα(α為常數)中,只有一個常數α,冪函數的所有性質都與冪指數α的取值有關,故由冪指數α可以確定冪函數的定義域、值域、單調性、奇偶性等。 編者的話:正確理解與掌握冪函數y=xα(α為常數)的概念、圖像特征與性質,以及與其他相應函數的概念、圖像與性質之間的關系,是解決涉及冪函數問題的根本所在。在實際求解冪函數及其應用問題時,既要重視“形”的作用,也要關注“數”的魅力。
三、冪函數的比較大小問題
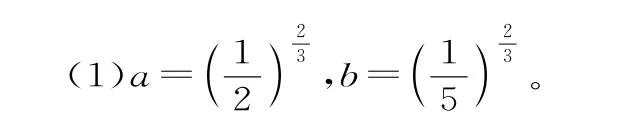


四、冪函數的綜合應用問題




