某型號轉向機上管柱仿真研究
郝佳偉,劉杰,趙鴻博,孫通,刑祚祥
(1.201800 上海市 博世華域轉向系統有限公司;2.200093 上海市 上海理工大學 機械工程學院)
0 引言
轉向系統是汽車最重要的部件之一,對安全性和駕駛舒適性有直接的影響。轉向系統一直受到汽車設計人員和生產制造商的廣泛關注,相關研究在過去幾十年中取得了重要進展。汽車上管柱結構作為汽車轉向系統的核心部件,連接了方向盤和車身橫梁,對汽車的行駛安全具有至關重要的作用。
近年來,學者們對轉向機系統的研究主要集中在結構設計、仿真優化以及控制等方面。Bu 等[1]為六輪電動汽車設計了一種具有較高靈活性的獨立轉向系統;李谷楠等[2]詳細闡述了管柱式助力轉向系統的結構;徐暢[3]通過ANSYS 軟件對轉向機的核心結構進行了實際工況的仿真分析和優化;李文中等[4]針對轉向支架進行了強度分析,并驗證了疲勞分析結果與實際壽命;Gao 等[5]通過數值方法研究了轉向系統剛度和阻尼對不同類型操作頻率下車輛瞬態特性的影響;米峻男[6]設計一種雙余度線控系統,提高了轉向系統的安全可靠性;此外,周全[7]針對齒輪齒條式動力轉向機進行了故障預測,為轉向機的壽命管理提供了重要的參考;Fu 等[8]提出一種基于風險優先級數的驅動系統容錯定量評價方法,并通過多體仿真研究了典型的失效模式的影響;Guo 等[9]針對液壓轉向系統高耗能等問題,提出了一種基于閉環泵控的電動輪式轉載機電液流量匹配轉向系統,通過實驗驗證該轉向系統能耗降低22.8%。以上研究更多關注轉向控制,針對上管柱的結構頻率分析很少涉及。
本文以簡化的轉向系統上管柱結構模型為例,采用ABAQUS 有限元仿真軟件,對其結構頻率及進行了仿真分析和試驗驗證,并研究了軸承支承剛度值對系統固有頻率的影響。
1 轉向機系統模型
1.1 三維模型
采用CERO 三維軟件建立了如圖1 所示的轉向系統模型,其由上管柱結構、中間軸、下管柱3部分組成。其中上管柱結構主要由上管柱和驅動單元組成,其三維模型如圖2 所示。

圖2 上管柱結構三維模型Fig.2 3D model of upper tube column structure
1.2 有限元模型
(1)動力學模型。由于上管柱結構太過復雜,工程實際中常進行簡化之后搭建有限元模型,建模后的動力學方程為
式中:M——質量矩陣;K——剛度矩陣;C——阻尼矩陣;x——系統的位移響應量;F——激振力。
(2)有限元模型建立。對上管柱結構進行分析時,由于上管柱結構以及連接關系復雜,在充分考慮實際工況的情況下,將有限元模型進行簡化。模型中的輸入軸、輸出軸、扭桿等都采用beam 單元進行等效代替,軸承采用Wire 進行連接,方向盤和電機采用集中質量單元mass 進行等效代替,簡化后的有限元模型如圖3 所示。其中鈑金件的材料為結構鋼,鑄造件的材料為鑄鋁,具體屬性如表1 所示。
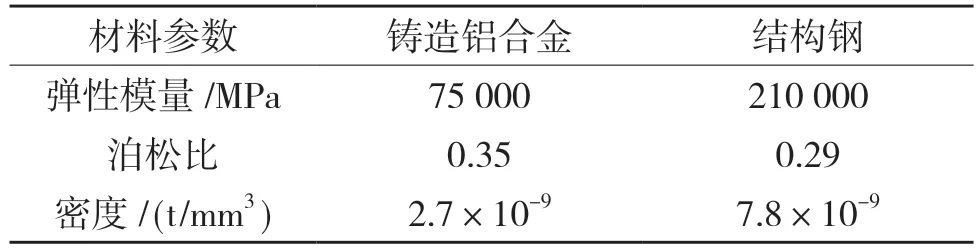
表1 結構的材料屬性Tab.1 Material properties of the structure
圖3 上管柱有限元模型Fig.3 Finite element model of upper tube column
2 結果分析
2.1 模態分析
假設系統在分析時不受到阻尼的影響,求解對系統的固有頻率。當系統沒有阻尼力時,此時系統的運動方程為
求得位移響應為
將式(3)代入式(2),得到
由于系統在振動過程中的振幅不全為0,所以
通過將方向盤總成2.56 kg 的質量施加在方向盤質心點處,采用ABAQUS 仿真軟件中Block Lanczos 得到上管柱系統的前6 階模態振型圖,如圖4 所示。可見,隨著模態階數增大,上管柱系統振動幅度越大。1 階模態時系統基本沒有發生變化;2 階模態時系統在水平方向上振動;3 階模態時系統在垂直方向上振動;4 階模態時系統在垂直方向上振動;5 階模態時系統在水平方向上振動;6 階模態時系統在水平方向上振動。
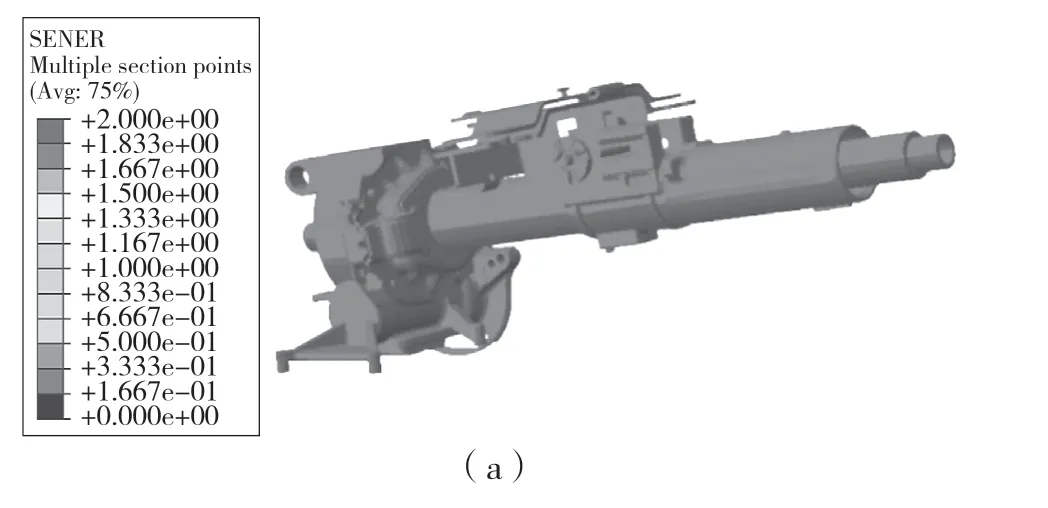
圖4 系統前6 階振型圖Fig.4 The first six orders of system vibration diagram
上管柱結構前6 階固有頻率如表2 所示,由表2 可知,在第4 階模態時系統固有頻率迅速變大,因此在實際工況中為防止汽車發生共振,需要避開系統的固有頻率。
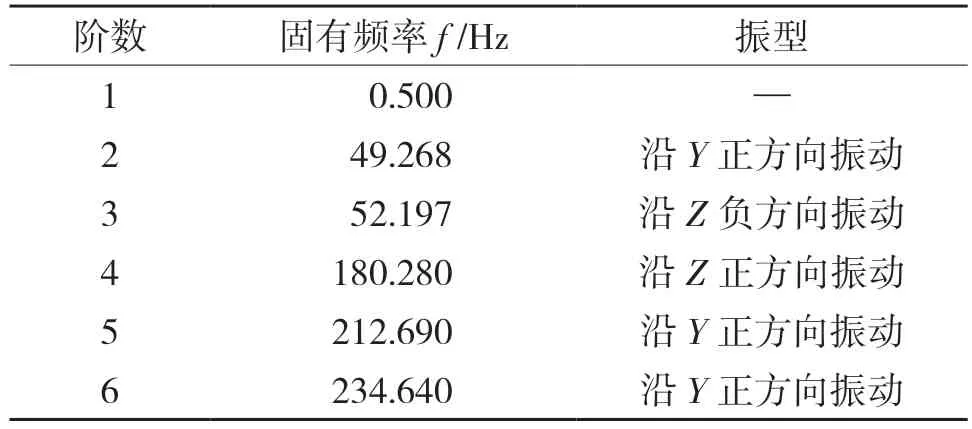
表2 上管柱結構前6 階固有頻率值Tab.2 The first six orders of inherent frequency values of upper tube column structure
2.2 試驗結果驗證
將轉向管柱固定于頻率試驗臺,管柱處于角度調節最下、長度調節最長位置,各附件固定夾緊,裝上實車用方向盤或等質量配重塊,配重塊重心位置同方向盤,測定固有頻率。圖5、圖6 分別為垂直和水平方向上的頻譜圖,垂直方向和水平方向的試驗頻率均為51 Hz。對比仿真結果可得,水平和垂直方向的誤差分別為3%和2%,滿足試驗要求。
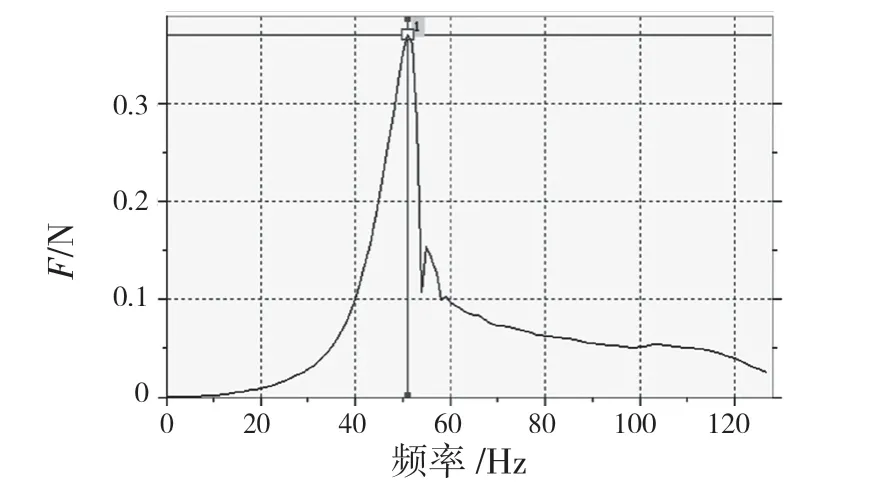
圖5 垂直方向上試驗頻譜圖Fig.5 Experimental spectrum in vertical direction
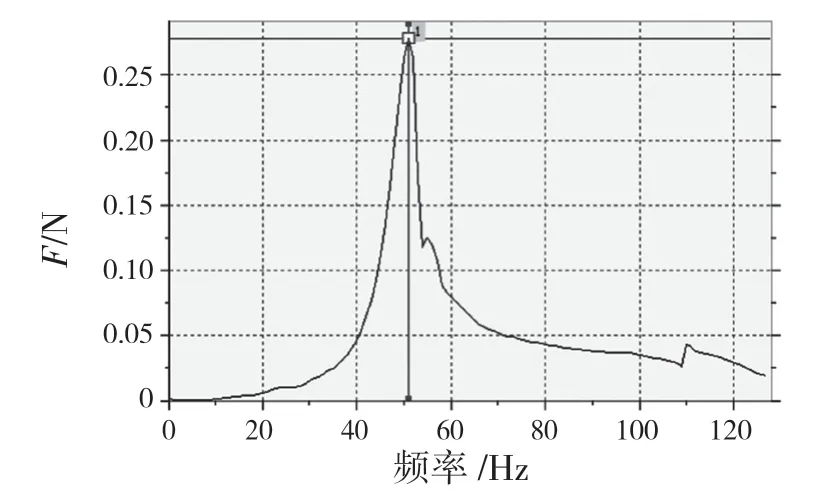
圖6 水平方向上試驗頻譜圖Fig.6 Experimental spectrogram in horizontal direction
3 軸承剛度對系統固有頻率的影響
實車管柱連接了方向盤和車身橫梁,串聯系統具有更大的柔性及更大的集中質量,故系統固有頻率更低,在路面或發動機激勵下,最低階模態容易被觸發,產生共振,從而導致轉向系統發生嚴重失效,甚至會導致車毀人亡。
由于上管柱各軸系通過支撐軸承進行連接,導致支撐軸承的剛度必然會對系統的固有頻率產生較大影響。改變上軸承的支承剛度研究系統固有頻率的變化,其中系統的固有頻率隨支承剛度值的變化如圖7 所示。由圖7 可見,隨著支承剛度增大,第1 階固有頻率基本不發生變化;第2 階到第6 階固有頻率在支承剛度為200~3 000 N/mm 的范圍內快速增大;當支承剛度超過3 000 N/mm 時,系統的固有頻率基本不發生變化,保持一個恒定值。因此在選取支承剛度值時需避開對固有頻率影響較大的區間。
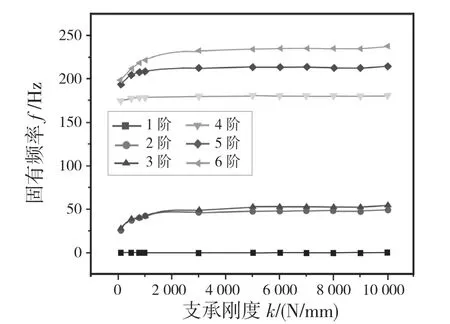
圖7 系統固有頻率隨支承剛度變化圖Fig.7 Variation of system inherent frequency with support stiffness
4 結論
本文以轉向系統上管柱結構為例,采用CREO建立了上管柱結構的三維模型,并根據實際工況建立了簡化的有限元模型,進行了模態分析和強度驗證,得到如下結論:
(1)通過模態分析得到了上管柱結構的前6階固有頻率和振型,并與頻率試驗結構進行對比驗證,證明了本次分析結果的準確性;
(2)改變支承剛度值,研究支承剛度對系統固有頻率的影響,分析得到隨著支承剛度的增大,系統固有頻率逐漸增大,然后趨于穩定。因此,需合理選取系統軸承支承剛度,避開可能引發共振的區間。

