基于狀態變換卡爾曼濾波的DVL/SINS組合導航算法
靳凱迪, 柴洪洲,*, 宿楚涵, 向民志, 李 明
(1. 戰略支援部隊信息工程大學地理空間信息學院, 河南 鄭州 450001;2. 鄭州航天宏圖北斗應用技術研究院有限公司, 河南 鄭州 450001)
0 引 言
水下無人自主航行器(unmanned underwater vehicle, UUV)在海洋測繪、水下資源探索和水下目標探測等任務中發揮著越來越重要的作用。獲取高精度的姿態、速度和位置等導航參數是UUV高效和安全完成任務的重要前提[1-3]。捷聯慣性導航系統(strapdown inertial navigation system, SINS)具有自主性、隱蔽性和主動性等優勢,可為UUV提供豐富的導航參數[4-5]。然而,受慣性測量元件(inertial measurement unit, IMU)誤差的影響,SINS定位誤差會隨時間迅速累積,因此必須使用輔助傳感器修正SINS累積誤差。
多普勒計程儀(Doppler velocity logger,DVL)/SINS組合導航系統是應用最為廣泛的UUV水下定位系統[6-7]。根據傳感器耦合方式的不同,DVL/SINS組合導航可分為松組合和緊組合[8],二者分別使用DVL三維速度和波束頻移作為Kalman濾波的量測信息[9-12]。然而,由于當前大部分DVL僅能提供三維速度,在實際情況中應用最為廣泛的仍為松組合方式。近年來,許多學者針對DVL/SINS組合導航Kalman濾波中的DVL誤差模型、非完整性約束和自適應濾波等問題展開了廣泛研究,有效提升了DVL/SINS組合導航系統的定位性能[13-16]。
DVL/SINS組合導航卡爾曼濾波中的狀態方程由SINS誤差方程構成。根據姿態誤差表達方式的不同,SINS誤差方程可分為歐拉角誤差模型和四元數誤差模型[17-18]。針對傳統SINS誤差模型不嚴密的問題,文獻[19]提出了一種基于矢量運算坐標系一致的誤差構建思想。在其基礎上,文獻[20]指出,傳統SINS速度誤差的定義只考慮了實際速度與理論速度大小的差異,而忽略了矢量坐標系不一致的影響。進一步,文獻[21]通過定義新的速度誤差提出了狀態變換卡爾曼濾波,并將其成功應用于全球衛星導航(global navigation satellite system, GNSS)系統/SINS組合導航、視覺/SINS組合導航和SINS初始對準等陸地場景[22-23]。文獻[24]和文獻[25]將速度誤差定義在計算導航系中,分別推導了GNSS阻尼SINS非線性誤差模型的歐拉角形式和四元數形式,并將其應用于GNSS/SINS大失準角對準中。
本文延續統一矢量運算中坐標系的思想,將狀態變換卡爾曼濾波引入DVL/SINS組合導航。首先,指出傳統SINS誤差方程中姿態誤差方程存在的坐標系不一致問題,進而構建了更為嚴密的SINS誤差方程;進一步,基于新定義的速度誤差推導了改進的DVL/SINS組合導航卡爾曼濾波狀態方程和量測方程;最后,利用仿真數據和船載實測數據驗證了本文所提算法的有效性。
1 坐標系定義
本文坐標系定義如下:
(1) 導航坐標系(n系):定義“東-北-天(E-N-U)”當地水平坐標系為導航坐標系;
(2) 計算導航坐標系(n′系):SINS實際計算時使用的導航坐標系,n′系與n系間的歐拉角稱為失準角φ;
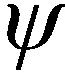
(4) DVL坐標系(d系):原點為DVL的幾何中心,x-y-z軸分別指向DVL框架的“右-前-上”方向,d系與b系間的歐拉角稱為DVL的安裝偏差角η,b系原點至d系原點的位移稱為DVL的桿臂誤差δl;
(5) 地球坐標系(e系):原點位于地球質心,x軸指向赤道與本初子午線的交點,z軸指向北極點,y軸與x軸和z軸構成右手坐標系;
(6) 地心慣性坐標系(i系):原點位于地球質心,x軸指向春分點,z軸指向北極點,y軸與x軸和z軸構成右手坐標系,i系不隨地球自轉而轉動。
2 狀態變換SINS誤差模型
2.1 傳統SINS誤差模型
SINS姿態可表示為歐拉角或四元數。在小失準角假設下,SINS的歐拉角誤差模型和四元數誤差模型均為線性,但四元數各分量的物理意義不明確,而且增加了誤差模型的維度,因此本文選擇歐拉角(失準角φ)描述SINS的姿態誤差。
傳統SINS姿態誤差模型為
(1)
速度誤差模型為
(2)

位置誤差模型為
(3)
式中:δp=[δL,δλ,δh]T為SINS的位置誤差;L、λ和h分別為SINS的緯度、經度和高程;Mpv和Mpp的具體形式為
(4)
(5)
式中:RMh=RM+h;RMh=RN+h;RM和RN分別為SINS所在位置的子午圈曲率半徑與卯酉圈曲率半徑。
2.2 改進的SINS誤差模型
(6)

(7)
其中,
(8)
(9)
根據式(6)定義的速度誤差,可將傳統速度誤差表示為
(10)
將式(10)代入式(7)可得
(11)
(12)
將式(11)代入式(1),可得
(13)
式中:
(14)
將式(14)代入式(13),得到新的姿態誤差方程:
(15)
式中:Map=M1+M2。
對式(6)兩側微分,可得
(16)
結合式(2)、式(13)和速度微分方程,式(16)可改寫為
(17)
將式(10)和式(11)代入式(17),有

(18)
由于
(19)
將式(14)和式(19)代入式(18)中并化簡,得到新的速度誤差方程:
(20)
將式(10)代入式(3),得到新的位置誤差方程:
(21)

3 DVL/SINS組合導航卡爾曼濾波
3.1 卡爾曼濾波狀態方程
DVL測速精度受水體溫度、鹽度和波束寬度等因素影響,在實際應用中一般將DVL觀測值建模為
(22)
式中:δk是建模為常值的刻度因子;wd為高斯白噪聲。
考慮DVL和SINS的誤差參數以及d系與b系間的安裝偏差角和桿臂誤差,在DVL/SINS組合導航卡爾曼濾波中選擇22維狀態向量:
(23)

因此,Kalman濾波狀態方程為
(24)
式中:Ft是由SINS誤差方程構成的狀態轉移矩陣;Gt為系統噪聲驅動矩陣;Wb為由陀螺和加速度計的白噪聲構成的狀態噪聲。
根據式(15)、式(20)和式(21),狀態轉移矩陣和系統噪聲驅動矩陣的具體形式為
--------------------
(25)
--------------------
3.2 卡爾曼濾波量測方程
DVL/SINS松組合中以三維速度作為卡爾曼濾波的量測信息。考慮DVL的安裝偏差角與桿臂誤差,由式(22)可得

(26)
由式(24),得到DVL/SINS組合導航量測方程為
(27)
綜上,DVL/SINS組合導航卡爾曼濾波數據融合過程如圖1所示。

圖1 DVL/SINS組合導航數據融合過程
4 實驗結果與分析
4.1 仿真實驗
為驗證DVL/SINS狀態變換Kalman濾波算法的有效性,首先設計如圖2所示的仿真軌跡進行實驗驗證。仿真軌跡總時長為800 s,包含如表1所示的加速、減速、勻速、橫滾和轉向等典型UUV運動狀態。軌跡初始位置為北緯30°、東經120°、高程0 m,初始速度為0 m/s,初始姿態角為[0°,0°,0°]。軌跡的初始水平失準角設為5′,初始天向失準角為30′,E-N-U3個方向的初始速度誤差均為1 m/s。

表1 仿真軌跡運動狀態

圖2 UUV仿真軌跡

為說明本文算法的有效性,使用常規DVL/SINS組合導航Kalman濾波(以“常規算法”表示)作為對比[28-29]。在相同條件下執行兩種算法,分別進行50次蒙特卡羅仿真實驗。
在姿態誤差上,由于兩種算法的水平姿態角估計精度均較高,在此僅對比天向失準角的估計效果。圖3給出了50次蒙特卡羅實驗中兩種算法的天向失準角平均值曲線。從圖3可見,本文算法的收斂速度更快。在0.5°初始天向失準角下,本文算法的平均天向失準角在280 s左右收斂到0.1°以下,而常規方式在560 s左右收斂到0.1°以下。導航結束時,常規算法的天向失準角為0.045°,本文算法的天向失準角為0.024°。因此,本文算法在一定程度上提高了DVL/SINS組合導航的姿態精度。

圖3 天向失準角平均值
DVL/SINS松組合直接以三維速度作為量測值,組合導航系統中速度誤差具有較強的可觀測性。圖4給出了兩種方案的E-N-U 3個方向速度誤差的平均誤差曲線。從圖4可見,兩種算法的速度誤差在DVL的約束下迅速收斂,且本文算法的水平速度估計效果優于常規算法,在測速精度和穩定性上均有一定程度的提升。經過初始收斂階段,在E-N方向上,常規算法的最大速度誤差分別為0.214 m/s和-0.069 m/s,而本文算法分別為0.142 m/s和-0.031 m/s,本文算法在導航前期有較高的速度精度。隨著導航進行,二者差異逐漸減小,在對準結束時,兩種算法在E-N方向上的速度誤差均為0.003 m/s和0.009 m/s。對比式(2)和式(20)可見,由于在新的速度誤差方程中由更穩定的重力矢量代替了式(2)中的比力信息,因此Kalman濾波狀態轉移矩陣更加穩定。

圖4 速度平均誤差
圖5給出了兩種方案E-N-U 3個方向的平均位置誤差曲線。由于DVL/SINS系統中位置誤差不可觀,因此解算的位置誤差是速度誤差累積的結果。從圖5可見,常規算法的E-N-U 3個方向的最大位置誤差分別為13.1 m、-8.9 m和-2.4 m,本文算法3個方向的最大位置誤差分別為8.1 m,-5.3 m和-2.6 m。在導航初始階段,本文算法的位置誤差發散得到了一定程度的改善。在導航結束時,兩種算法的定位誤差的差異在毫米級。

圖5 位置平均誤差
圖6~圖8給出了兩種方案的DVL的刻度系數、安裝偏差角和桿臂誤差的50次實驗平均值曲線。從圖中可見,對于可觀性較強的狀態參數,如x軸-z軸安裝偏差角、刻度系數和桿臂誤差,兩種算法的估計效果較為接近,均可估計出添加的誤差參數。對于可觀性較差的狀態參數,兩種算法有一定差異,且均無法準確估計。

圖6 DVL刻度系數平均值

圖7 DVL安裝偏差角平均值

圖8 DVL桿臂誤差平均值
4.2 船載實驗


圖9 船載平臺及設備
實驗使用高精度后處理軟件Novatel Inertial Explorer(IE)的GNSS-RTK/SINS前后向平滑緊組合的輸出作為參考基準。由IE結果獲得軌跡的初始位置為北緯30.577°,東經114.472°,高程19 m。船載軌跡如圖10所示。

圖10 武漢湖試軌跡
為了避免DVL桿臂誤差、安裝誤差角和刻度系數對導航參數的影響,使用文獻[30]算法對實測數據中的DVL誤差參數進行了預標定。實驗中,在IE參考值的基礎上,設置軌跡的初始水平失準角為0.5°,初始天向失準角為1°,E-N-U 3個方向速度誤差均為1 m/s。
使用常規算法與本文算法分別對該軌跡進行處理。圖11給出了兩種算法估計的天向失準角對比。從圖11可見,在導航前期二者的差異較為顯著,本文算法的最大天向失準角誤差為-2.390°,常規算法為-4.199°。隨著導航進行,二者差異逐漸減小,在導航結束時常規算法和本文算法的天向失準角分別為-0.040°和0.017°。因此,在補償了坐標系不一致誤差后,組合導航系統估計的姿態精度更高。

圖11 湖試中的天向失準角
圖12給出了兩種算法的速度誤差估計曲線。從圖12可見,兩種算法的天向速度有基本一致的估計精度。在E-N方向上,常規算法的最大速度誤差分別為-0.214 m/s和0.172 m/s,而本文算法的最大速度誤差分別為-0.105 m/s和0.098 m/s。因此,本文算法在導航前期的測速精度較高,隨著導航進行,兩種算法速度誤差的差異逐漸減小。

圖12 湖試中的速度誤差
圖13給出了兩種算法的位置誤差估計曲線。從圖13可見,常規算法和本文算法的水平最大位置誤差分別為18.700 m和14.239 m。當導航結束時,常規算法和本文算法的水平位置誤差分別為4.937 m和3.109 m。這是由于本文算法的速度誤差較小,而位置誤差受速度誤差累積的影響。統計兩種算法估計的姿態、速度和位置均方根差(root mean squared error, RMSE)如表2所示。從表2可見,本文算法的姿態、速度和位置的精度較常規算法均有一定程度的提升。其中,天向失準角RMSE降低了43%,東向速度RMSE降低了34%,北向速度RMSE降低了31%。本文算法的東向位置誤差和北向位置誤差的RMSE分別降低了28%和10%。

表2 湖試中導航參數RMSE統計結果

圖13 湖試中的位置誤差
5 結 論
為了提高DVL/SINS組合導航系統的定位精度,考慮SINS速度誤差中坐標系不一致的問題,提出了一種基于狀態變換Kalman濾波的DVL/SINS組合導航算法。在分析傳統SINS誤差方程中存在坐標系不一致誤差的基礎上,詳細推導了改進的狀態變換SINS誤差方程;進一步地,構建了DVL/SINS組合導航Kalman濾波方程。實驗結果表明,該算法可以有效處理傳統速度誤差中坐標系不一致的影響,在一定程度上提高了DVL/SINS組合導航系統的精度。

