萬有引力與宇宙航行常見問題及解題策略
王華明
(湖北省仙桃市田家炳實驗高級中學)
萬有引力與宇宙航行作為高考的熱點題目,幾乎在每年的高考中都會以選擇題的形式出現.在問題設置上,通常會考查研究對象的運動參數、軌道變化、能量等諸多問題,因為涉及較多公式,學生解答比較困難.本文結合實際情況,對相關問題進行分類總結,以此促進學生的掌握.
1 中心天體的質量和密度
例1恒星S2 不同時間所處位置如圖1 所示,其運動軌跡是半長軸為1000 AU(太陽距地球為1AU)的橢圓,銀河系中心可能存在超大質量黑洞,若認為S2所受力主要來自該黑洞的引力,設太陽的質量為M,則黑洞的質量約為( ).
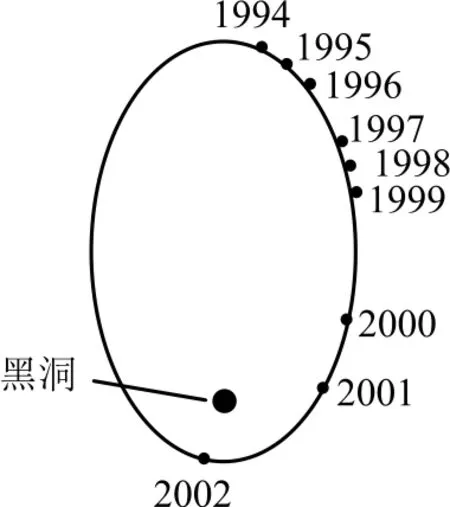
圖1
A.4×104MB.4×106M
C.4×108MD.4×1010M
2 天體運行參量分析
由上述各公式可以看出,天體運行軌道越高,其運行的線速度、角速度、加速度等都會減小,運行周期越長.
例2金星、地球與火星繞太陽做勻速圓周運動,向心加速度分別為a金、a地、a火,運行速率分別為v金、v地、v火,已知R金<R地<R火,則可得( ).
3 變軌問題
如圖2所示是常見的變軌問題模型,速度、加速度、周期存在以下特點:

圖2
1)速度:設衛星在軌道Ⅰ、Ⅲ上速度分別為v1、v3,在軌道ⅡA、B點速度分別為vA、vB,在A點加速,則vA>v1,在B點加速,則v3>vB,因為v1>v3,所以有vA>v1>v3>vB.
2)加速度:在同一圓軌道上,所有時刻加速度大小均相等.
4 雙星問題
雙星模型是考試中常見的一類問題,此類模型中,兩個距離較近的行星在彼此引力的作用下繞某一點做圓周運動,如圖3所示.
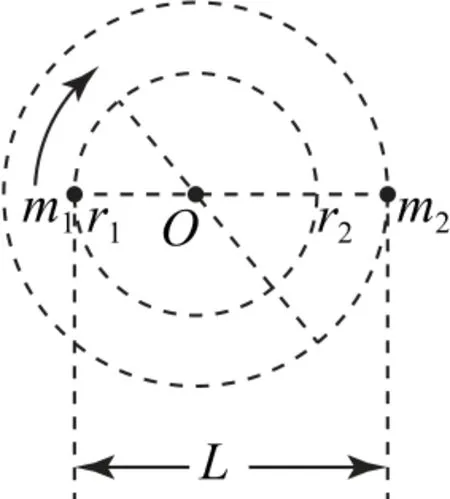
圖3
雙星模型的運行軌道為同心圓;二者的F向、T、ω相等,r1+r2=L,半徑與質量成反比.在解答這類問題時,需要借助公式
例3兩中子星相距約400km,繞某點每秒轉動12圈,將中子星視為分布均勻的球體,根據所學知識可估算出某一時刻兩顆中子星( ).
A.質量之積 B.質量之和
C.速率之和 D.自轉角速度
5 近地衛星、同步衛星及赤道上物體的運行問題
對近地衛星、同步衛星有F萬=F向,兩者都圍繞地球做勻速圓周運動,則有r近<r同,所以a近>a同,v近>v同,ω近>ω同,T近<T同.
同步衛星與赤道上的物體角速度相同,則有ω同=ω物,T同=T物,因為r同>r物=R,由v=ωr,a=ω2r可知,v同>v物,a同>a物.
綜上,近地衛星、同步衛星與赤道上物體相比,有r同>r近>r物,v近>v同>v物,ω近>ω同=ω物,T近<T同=T物,a近>a同>a物.
例4如圖4所示,a、b、c、d四顆地球衛星,其中a在赤道上未發射,b為近地軌道衛星,c為同步衛星,d為高空探測衛星,則( ).

圖4
A.c、d向心加速度相同
B.相同時間內,b轉過的弧長最長
C.4小時c轉動的角度為
D.b的周期小于d
綜上所述,本文總結了萬有引力與宇宙航行中常見的5大類題型,并且給出了解答問題常用的相關公式.學生應當熟練掌握各類題型及解題策略,在面對相關問題時才能快速解答.
(完)

