基于能量最小原則的高鐵填料壓實過程振動參數優化

陳曉斌，謝康，堯俊凱，惠瀟涵，王業順，鄧志興

(1.中南大學 土木工程學院，湖南 長沙，410083；2.中南大學 教育部重載鐵路工程結構重點實驗室，湖南 長沙，410083；3.中國鐵道科學研究院集團有限公司 鐵道建筑研究所，北京，100081；4.中國鐵路廣州局集團公司，廣東 廣州，510440)

為了保證高鐵路基的安全性并提高列車運行的舒適性，對路基填料的級配、最大粒徑、形狀均有著嚴格的標準[1-3]。相比于堆石壩、公路的填料選取，高鐵填料填筑時需要沿線設立填料廠，從而保證高鐵填料質量[3]。傳統的高鐵路基振動壓實質量檢測一般采用試坑取樣法，分別對采用靜壓、弱振、強振等振動參數下的壓實結果進行抽樣檢測[4]。然而，該方法忽略了填料離散性問題，導致壓實效率低、壓實不均勻等問題。

壓實過程控制是近期研究的熱點，學者們提出了許多理論和技術，并將其應用于壓實過程控制[5-8]，主要包括連續壓實控制(continuous compaction control，CCC)和智能壓實(intelligent compaction，IC)。CCC 是指在振動壓實過程中，基于機土耦合相互作用原理處理振動輪豎向振動信號，建立壓實質量控制體系[9]。雖然CCC 已在鐵路建設中得到廣泛應用，但是仍然存在缺陷，主要表現在缺少對壓實過程中振動參數的改進研究[10]。填料壓實狀態會隨著壓實過程不斷發生變化，根據填料壓實狀態不斷調整振動參數，而不是采用固定的壓實參數。國外將CCC 與壓路機振動工藝參數調節功能結合起來，又被稱作“智能壓實(IC)”[9-10]。在振動過程中，如何調整振動參數一般由駕駛員操作來實現，其本質上屬于人工控制的范疇。智能壓實則是在沒有人員參與的情況下，利用壓路機的自動調節控制裝置，基于填料的壓實狀態自動調整振動參數。目前，智能壓實很難到達自動調參的功能，仍需要進一步完善。

現階段針對振動參數(振幅A0、振動頻率f、振動時間t)研究仍為不同振動參數下動力響應問題。文獻[11-13]分別采用有限元法和離散元法對振動壓實過程進行模擬，量化出振幅、頻率等振動參數對壓實質量的影響，難以在模型中精確模擬機理。文獻[14-15]基于試驗方法，研究振動參數對壓實質量的影響，但是以上研究主要是揭示單一振動參數對壓實效果的影響，缺少壓實過程中的振動參數的改進成果。伴隨著無級調幅調頻壓路機出現，可以在壓實過程中對壓路機進行連續調頻、調幅。德國BOMAG公司、瑞典Dynapac公司以及日本SAKAL公司等能根據填料的壓實狀態自動選擇振動參數以達到較高的壓實效率[16]。然而，上述的研究均通過調整振動參數，使得下一次壓實度取得最大值，屬于局部改進。而在壓實過程中振動參數需要實時改進，使得填料更好、更快地達到最佳密實狀態。同時，激振能量過大，容易導致振動壓實設備出現“跳振”現象，這會減少振動壓實設備的使用壽命，也會造成顆粒破碎增多，形成路基不均勻沉降病害[17-18]。因此，有必要在壓實過程中實時改進振動壓實參數，即基于填料的壓實狀態來實時調整壓實參數，優化壓實方法。

綜上所述，目前缺乏壓實過程中振動參數的動態優化方法，這限制了智能壓實的發展，同時，振動參數過大容易引起壓實設備損耗、顆粒破碎問題。為此，本文提出了一種基于能量最小原則的振動參數動態改進方法。首先，開展不同振動參數的振動壓實試驗，揭示振動參數與干密度的關系；其次，采用改進BP神經網絡建立了干密度增量預測模型，根據能量最小原則采用遺傳算法構建了壓實過程振動參數優化方法；最后，基于Modbus 通訊，設計可振動參數可調的智能振動壓實儀，并通過振動壓實試驗對改進結果進行驗證和應用。

1 試驗材料與方法

1.1 試驗材料

試驗材料取自于廣湛高鐵新興段路基粗粒土填料，為花崗巖隧道礦渣，具有質地緊密、棱角較多等特點。填料的級配如圖1所示。該填料級配最大粒徑為45 mm，曲率系數為1.0，不均勻系數為80，最優含水率為6%。

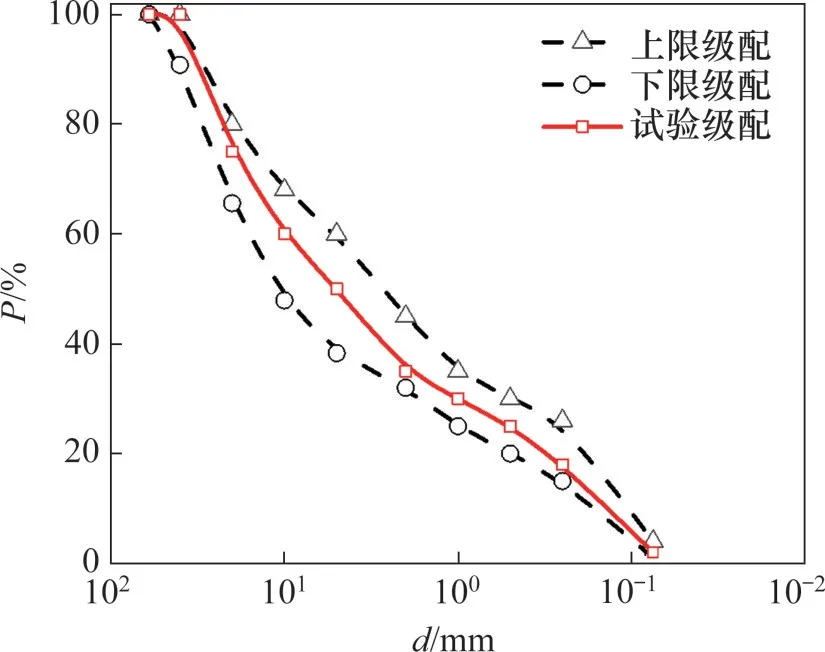
圖1 試驗材料的級配曲線Fig.1 Grain-size distribution curves of tested materials

1.2 試驗儀器

試驗采用自主研發的多參數可調式智能振動壓實儀，如圖2所示。設備振動單元空載單元質量為500 kg，配重塊的質量M調節范圍為0～480 kg，偏心距e0的調節范圍為0～8 cm，偏心塊m0質量范圍為4.8～14.4 kg，振動頻率f為0～40 Hz。在壓實過程中，內置位移傳感器可實時采集填料沉降，基于表面沉降理論[19]，可自動輸出干密度-時間曲線。

圖2 智能壓實設備示意圖Fig.2 Diagram of intelligent compaction equipment

1.3 試驗方法

振動壓實試驗主要包括以下3個步驟。

1)制樣。將篩分得到的填料曬干，取質量分數為6%的水均勻噴灑于填料上，充分拌勻；將壓實桶(內徑為152 mm)內部涂潤滑油，裝入5 kg 填料拌勻；將壓實桶置于振動壓實儀下端固定位置處，使壓縮板能恰好進入壓實桶內。

2)振動壓實。接通電源后，在圖2所示的智能振動壓實儀中預設f和t這2 個參數，并點擊開始按鈕。

3)數據采集。振動壓實過程中采集試樣干密度。壓實桶與填料顆粒最大粒徑比為3.8，滿足規范[3]中對壓實桶尺寸的要求。試驗過程中模擬了多種工況，其中設t為4 min，振幅A0為0.15、0.30和0.60 mm，振動頻率f為10、15、20、25和30 Hz。

2 粗粒土填料壓實特性

2.1 振動參數

試樣干密度隨振動時間變化規律如圖3(a)所示。從圖3(a)可見：試樣的干密度均隨振動時間增加而呈現對數增長趨勢。在不同振動頻率下，試樣獲得最大干密度的振動時間是不同的。經對比發現，設置振動時間為4 min是合理的，即獲得各組工況下的試樣干密度穩定值。如無特殊說明，以下的干密度均代表振動4 min之后的干密度。

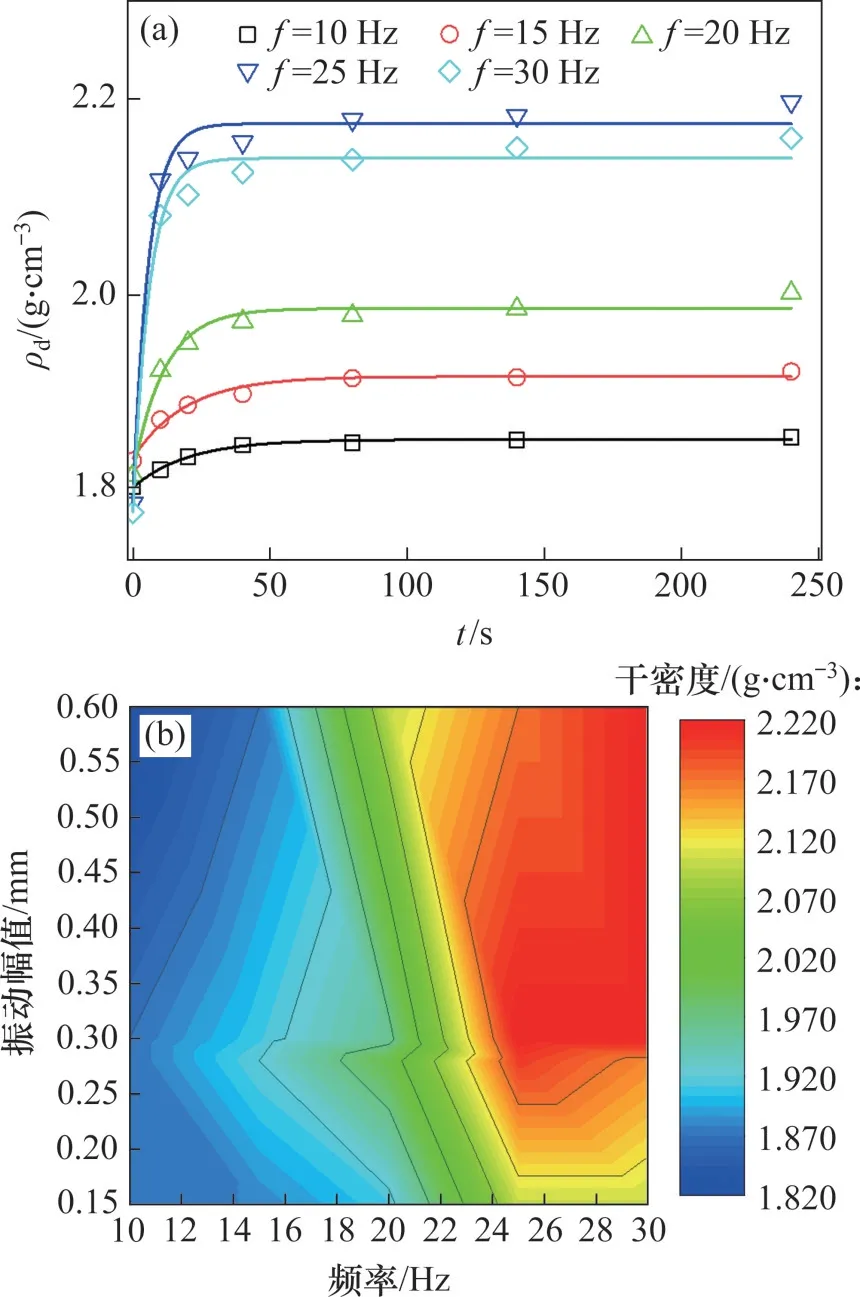
圖3 不同工況試樣干密度演化Fig.3 Evolution of dry density of specimens with different working conditions

從圖3(a)可以發現：在不同振動頻率下，填料的干密度不一樣，這表明振動頻率和振動幅值也會對填料干密度有重要的影響。圖3(b)所示為振動頻率和幅值與填料干密度的關系云圖。無論振動參數為小頻率、大振幅，還是大頻率、小振幅，都很難獲得較大的干密度，這主要是因為外界提供給填料壓實條件使得填料顆粒只能在原位置附近進行小范圍振動或者顆粒之間沒有相對運動，無法有效填充填料顆粒結構中的大孔隙。只有在f≥25 Hz，A0≥0.3 mm時，試樣能到達到最大干密度為2.22 g/cm3。當外界振動頻率處于填料固有頻率(25～30 Hz)時，填料顆粒處于共振狀態，顆粒之間相對運動加劇，同時，振動幅值主要與填料高度相關，當外界振動幅值為0.3 mm 時，容器底部填料運動加劇，進而獲得較大的干密度。

2.2 振動荷載和振動強度

在振動壓實中，填料受到周期性的激振力作用，而使內部產生剪切應力，壓實填料，激振力F計算式如下：

式中：Mp為振動系統質量；Ao為振幅；f為振動頻率。

壓實桶的直徑×高度為15.2 cm×11.2 cm，填料上振動荷載Ps計算方法如下：

式中：S為激振頭與壓實桶的接觸面積。

進一步，完整的振動壓實工藝主要由設備靜載、振動頻率以及激振力所組成，三者的影響可以歸納為振動強度E的作用，計算方法如下：

式中：W為壓實儀靜載。振動荷載、強度與干密度的關系如圖4所示。

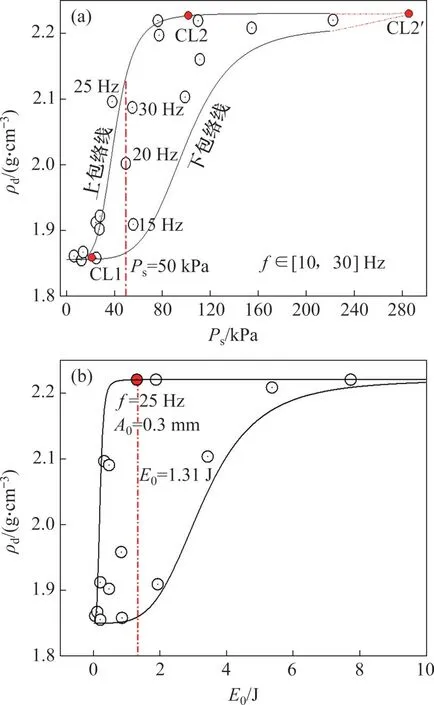
圖4 干密度與振動荷載、強度的關系Fig.4 Relationship between dry density and vibration load and strength

由圖4(a)可知：干密度隨著振動荷載增加而呈現出“緩慢增長—快速提高—平穩”3個階段。

1)當振動荷載≤20 kPa時，試樣干密度處于緩慢增長階段，此時，試樣所受動應力較小，顆粒之間相對運動較弱。

2)當振動荷載為20～110 kPa 時，試樣干密度處于迅速提高階段，顆粒之間振動響應增強，細顆粒可以迅速填充到粗顆粒孔隙中。

3)當振動荷載＞110 kPa 時，干密度增長趨于穩定。而較大的振動荷載會加劇試樣的破碎，造成試樣級配變異，進而影響壓實質量。振動荷載與試樣干密度之間有一個包絡區域，處于上包絡線區域的振動荷載對應的共振頻率為25～30 Hz，相反，下包絡線區域的振動荷載對應的振動頻率較低。即對于上包絡線而言，較小的振動荷載可達到較大干密度。

同樣地，振動強度與干密度之間也呈現出“緩慢增長—快速提高—平穩”3 個階段。同時，振動強度存在閾值使得干密度達到最大值，后期的干密度趨于穩定。進一步增大振動強度會導致設備產生“跳振”現象，顆粒破碎加劇，嚴重影響設備壽命。

3 基于能量最小原則粗粒土壓實質量動態優化方法

3.1 粗粒土壓實質量動態優化算法

試樣干密度并不是隨著外部振動能量增加而增加。激振能量過大會導致振動壓實設備出現“跳振”現象，也會造成試樣顆粒破碎增多。隨著試樣壓實度增加，試樣的壓實性能不斷發生改變。理論上，每個壓實狀態均對應一個最優振動參數。因此，可以將試樣的振動參數改進過程看作一個多階段決策問題，每次振動參數的調整均對應一次決策。試樣從松散狀態到密實狀態是一個完整的振動壓實過程，對于每個階段的振動參數選取需要考慮該階段的決策對整個振動壓實階段的影響。

以填料壓實度達到規范中要求的壓實標準為基礎，壓實度計算如式(4)所示。為了保證整個振動壓實過程中的能量輸出最小，進而提高壓實效率，將整個振動壓實過程中的輸出能量相加，輸出總能量計算如式(5)所示。

式中：ρdi為第i狀態下試樣干密度；Δρdi為振動壓實過程中試樣的第i次相比于i-1 次的干密度增量；ρdi-1為第i-1 狀態下試樣干密度；A0i為第i狀態下所選擇的振動幅值；fi為第i狀態下所選擇的振動頻率；K為壓實度，高鐵基床壓實度取95%。

參數n通過干密度增量函數確定，每振動一次所增加的干密度與試樣當前壓實狀態、振動頻率和振動幅值有關，即滿足式(6)。i=0，代表靜壓狀態。當i＞0時，第i狀態下的試樣干密度等于第i-1狀態下試樣干密度與第i狀態下試樣干密度增量之和，第i狀態下試樣干密度增量則通過第i-1狀態下試樣干密度與第i狀態下試樣所選擇的A0i和fi來確定，計算公式如式(7)所示。

為了實現上述動態優化過程，首先，采用改進BP 神經網絡建立了干密度增量預測數學模型；然后，基于GA 求解振動參數優化方法，其中GA的適應度函數是根據能量最小原則建立；最后，通過室內試驗驗證優化結果。優化算法流程圖如圖5所示。

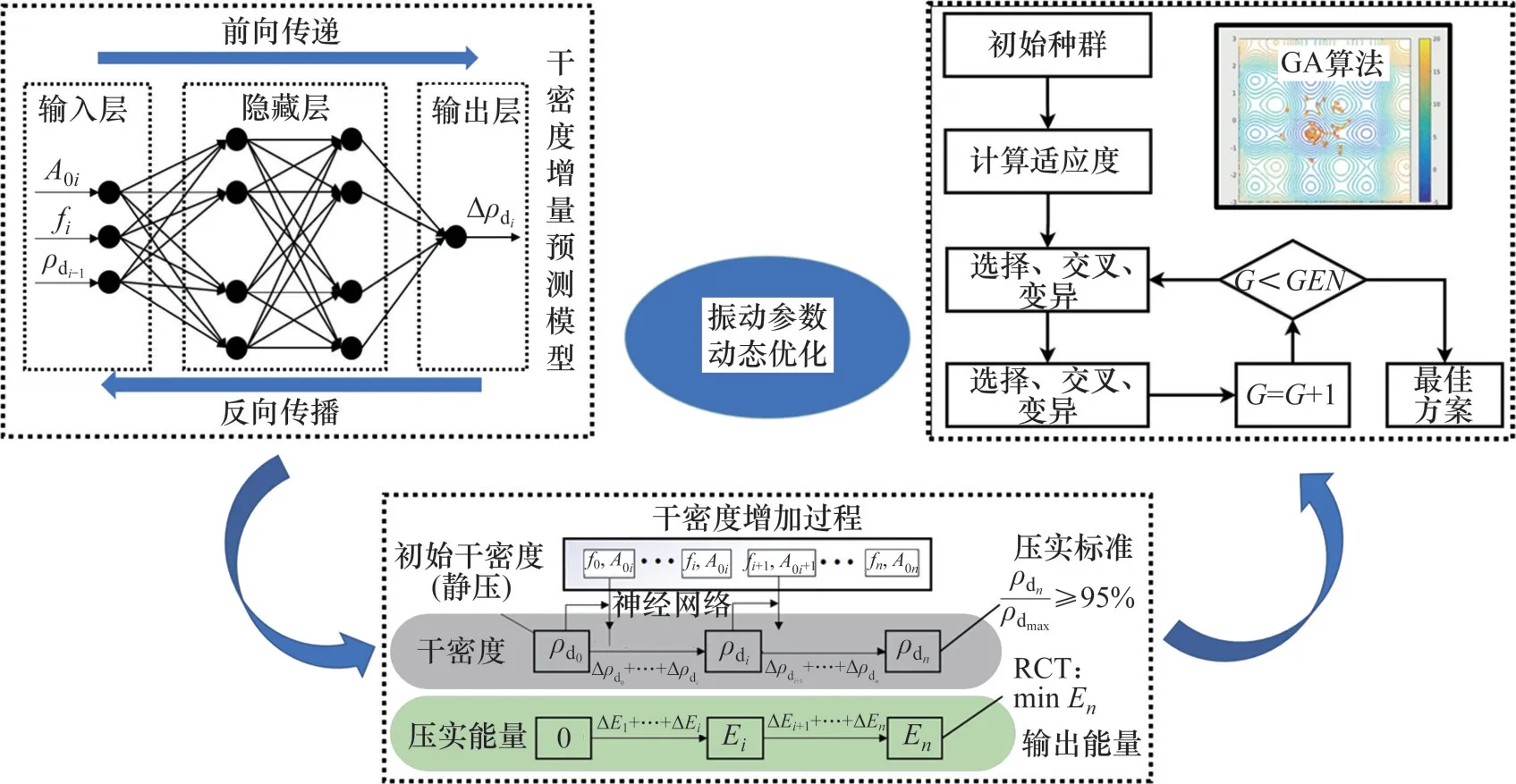
圖5 基于能量最小的動態優化算法流程圖Fig.5 Flow chart of dynamic optimization algorithm based on energy minimization

試樣的干密度根據改進的BP 神經網絡預測得到的干密度增量值累加得到，干密度增量預測模型構建主要包括3個部分即構建數據集、模型訓練和模型測試，如圖6所示。

圖6 改進BP干密度增量預測模型流程圖Fig.6 Flow chart of improved BP dry density incremental prediction model

1)構建數據集。基于干密度-時間試驗結果，建立試樣振動壓實過程振動次數與干密度間預測模型。基于試驗發現，各個工況下干密度與振動次數關系符合雙曲線模型。

式中：a和b分別為變量參數。

為消除不同變量的維度關系，需要對干密度進行歸一化處理。

式中：y*為標準化后值；y、ymin和ymax分別為變量實際值、標準化區間的最大值和最小值。

將式(8)代入式(9)，即得到干密度與振動次數預測模型：

式中：ρd為當前狀態密度；ρmax為當前工況下壓實穩定狀態干密度，即最大干密度；ρ0為初始狀態干密度；n為振動次數。

根據式(10)計算得到各工況下的模型參數，如表1所示，從表1可見：采用雙曲線模型對壓實過程干密度變化進行預測具有較高精度。

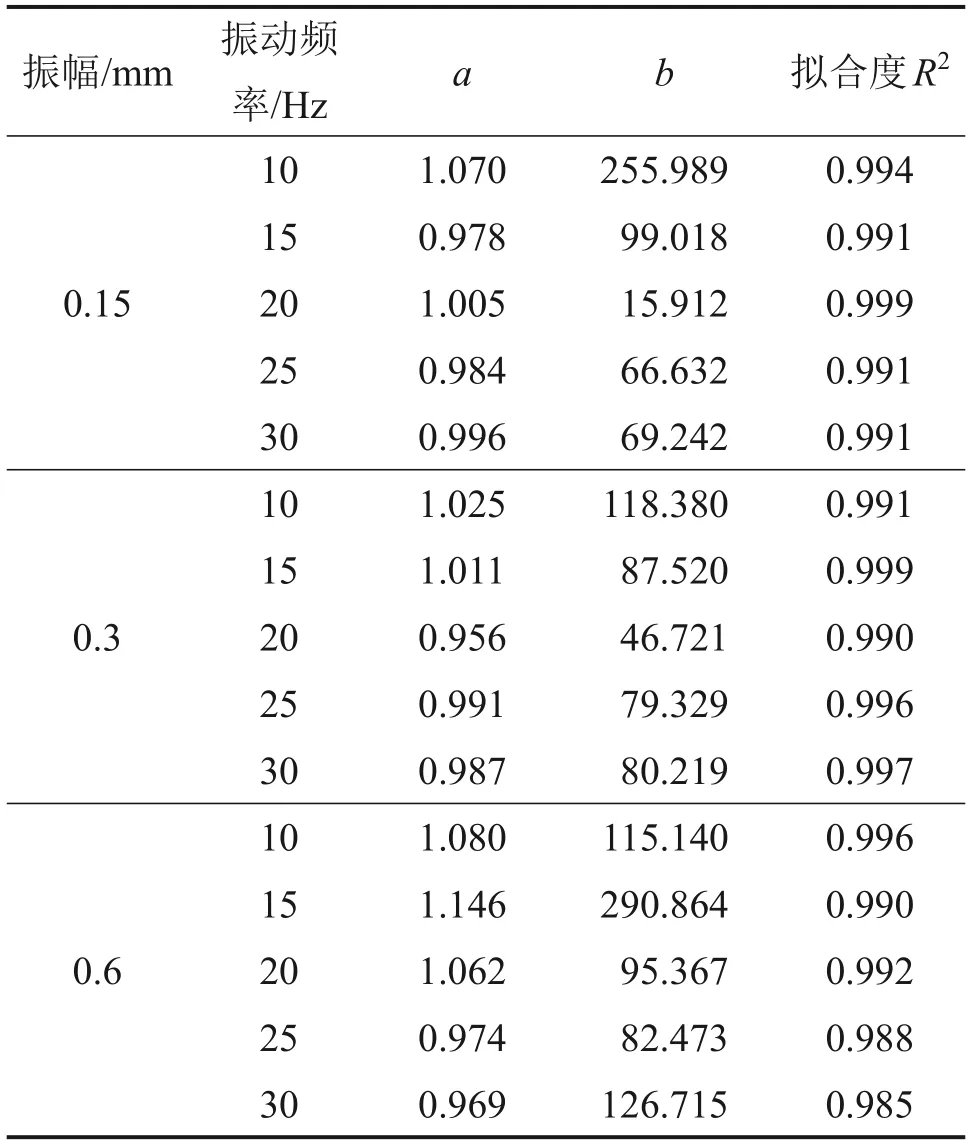
表1 模型參數及相關系數Table 1 Model parameters and correlation coefficients

以連續振動20 次為1 次完整振動，然后進行調頻調幅操作，獲得7 500組訓練數據集。將數據集隨機劃分為訓練集、驗證集和測試集3 個部分，數據量占比分別為70%、15%和15%。

2)模型訓練。在實際應用中，BP 神經網絡算法也有幾個不足之外，包括容易陷入局部最優、樣本依賴性和學習率不可調等，從而使得干密度增量預測模型收斂速度慢甚至不收斂，最終影響干密度增量預測的精度。為了解決以上的問題，在傳統BP神經網絡的基礎上引入改進學習率改進器AdamOptimizer算法，該方法根據損失函數的變化合理調整學習率，加速模型收斂速度[20-22]。

3)模型測試。干密度增量預測模型訓練完成后被保存，測試時調用該模型，并將測試集輸入。測試完成后，判斷測試結果的誤差是否小于設定誤差，若滿足則可應用該模型，反之重新執行步驟2)。

3.2 GA算法超參數優化

遺傳算法的主要參數包括種群數量(PS)、選擇概率(SP)、交叉概率(CP)和變異概率(Mu)[23-24]，參數的取值影響著模型的精度和計算效率。取改進后的能量和遺傳代數分別作為精度和計算效率判斷的標準。為了保證計算速度和改進效果，在實際改進之前設置不同的初始參數并進行對比，最終確定遺傳算法的合理參數。

在保持遺傳代數為200 代，選擇概率為0.90，交叉概率為0.70，變異概率為0.005不變的前提下，分別設置種群數量為50、100、150、200、250 和300個開展試驗。不同種群數量適應度隨遺傳代數的變化曲線如圖7(a)所示，由圖7(a)可見，遺傳到125 代時，這6 種適應度均逐漸收斂，收斂速度隨種群數量增加而減小。為提高計算效率，最終確定種群數量為150個，遺傳代數為200代。

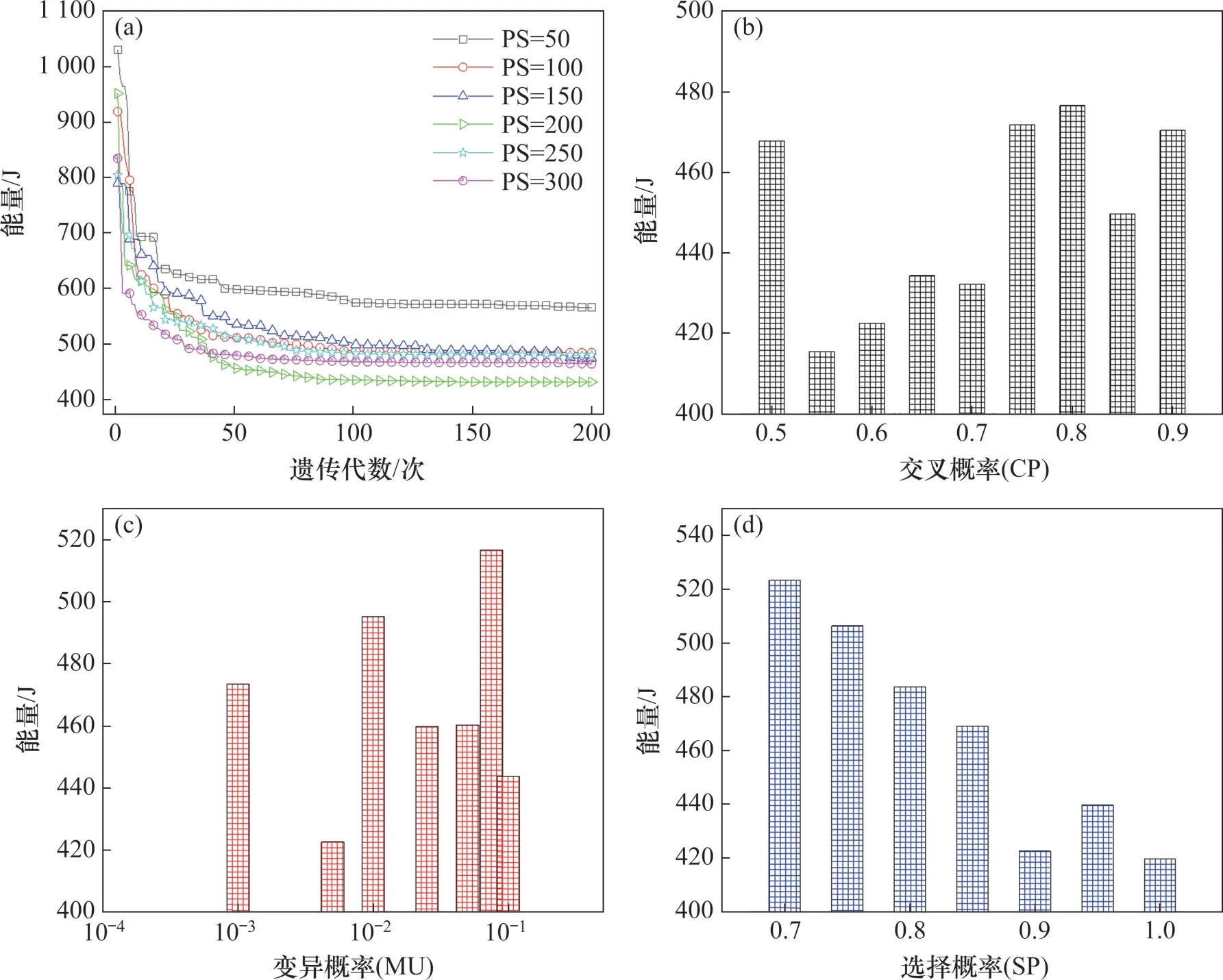
圖7 GA算法參數選取Fig.7 GA algorithm parameter selection

遺傳算法中建議的交叉概率為[0.50，1.00]之間。因此，設置交叉概率為0.50，0.55，0.60，0.65，0.70，0.75，0.80，0.85，0.90，在保證種群數量為150 個、選擇概率為0.90、變異概率為0.005 不變的前提下，得到適應度變化如圖7(b)所示，當交叉概率在[0.55，0.70]之間時，改進結果較為穩定，最終確定交叉概率為0.60。

遺傳算法中建議的變異概率為[0.001，0.100]之間。設置變異概率為0.001、0.005、0.010、0.025、0.050、0.075、0.100，將種群數目設置為150，將選擇概率設置為0.9，將變異概率設置為0.60，得到適應度與變異概率關系如圖7(c)所示，變異概率過大容易使得適應度高的個體發生變異，導致改進結果收斂速度過慢，當變異概率位于[0.010，0.050]之間時，改進收斂速度快且改進結果較穩定，最終確定變異概率為0.025。

設置選擇概率為0.70，0.75，0.80，0.85，0.90，0.95，1.00，種群數量為150，交叉概率和變異概率分別設置為0.60 和0.005，根據其計算的適應度來評估此組參數下改進結果的精度，適應度變化如圖7(d)所示。從圖7(d)可見：選擇概率越大，改進后能量越小，為防止求解過程陷入局部最優解，最終確定選擇概率為0.90。

通過分析遺傳算法參數，最終設置種群數量(PS)為150，選擇概率(SP)為0.9，交叉概率(CP)為0.6，變異概率(Mu)為0.05。

4 粗粒土壓實質量動態優化算法應用

4.1 干密度增量模型預測結果

在訓練集和測試集上，分別對傳統的BP 神經網絡和改進的BP神經網絡進行模擬訓練，得到模型在訓練過程中的訓練集損失值(簡稱loss)與驗證集損失值(簡稱val_loss)變化規律如圖8所示。

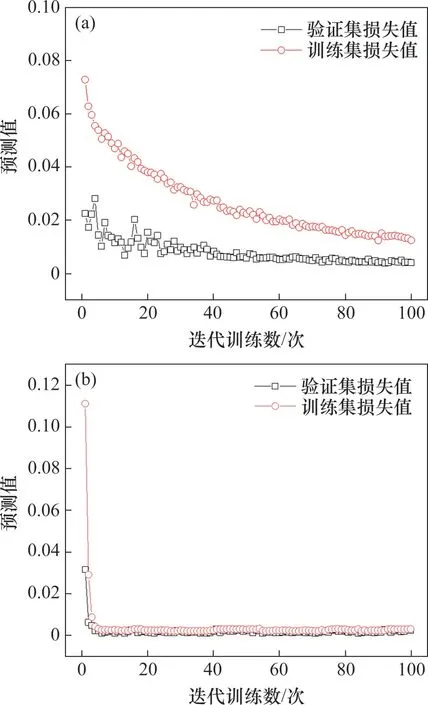
圖8 兩類模型的訓練集和驗證集損失函數曲線Fig.8 Loss function curves for training and validation sets of two types of models

從圖8(a)可見：傳統的BP 神經網絡模型在訓練過程中訓練集損失值和驗證集損失值下降速度慢且持續震蕩，在100輪結束時，訓練集損失值曲線仍未收斂，這主要是由于傳統的BP神經網絡使用SGD 算法，并沒有引入動量法，并不能使梯度向量向相關方向加速變化，導致震蕩現象。從圖8(b)可見：改進的BP 神經網絡模型在訓練過程中訓練損失和驗證損失下降速度非常快；在第5輪迭代后，訓練集損失值和驗證集損失值便開始收斂，且未出現震蕩現象，這是由于改進的BP神經網絡引入了動量法，從而達到加速收斂的目的。同時，在整個迭代運算過程中，驗證集損失值均小于訓練集損失值，在迭代結束時，訓練集損失值和驗證集損失值都已經收斂完成，兩者均接近于0，說明改進的BP神經網絡模型訓練效果較好，且在驗證集上具有較強的泛化能力。

綜上所述，改進的BP 神經網絡模型具備可調節、收斂快的特點，解決了傳統的BP神經網絡模型收斂慢、容易陷入局部最優點的問題。

為了進一步測試模型的準確性，選擇未參與訓練的1 125組振動試驗數據，同時采用已經訓練好的傳統BP 和改進BP 模型分別進行預測，并采用均方誤差MSE和平均絕對誤差MAE來評估預測結果。計算方法如式(11)和(12)所示，預測結果與實際值進行對比如圖9所示。

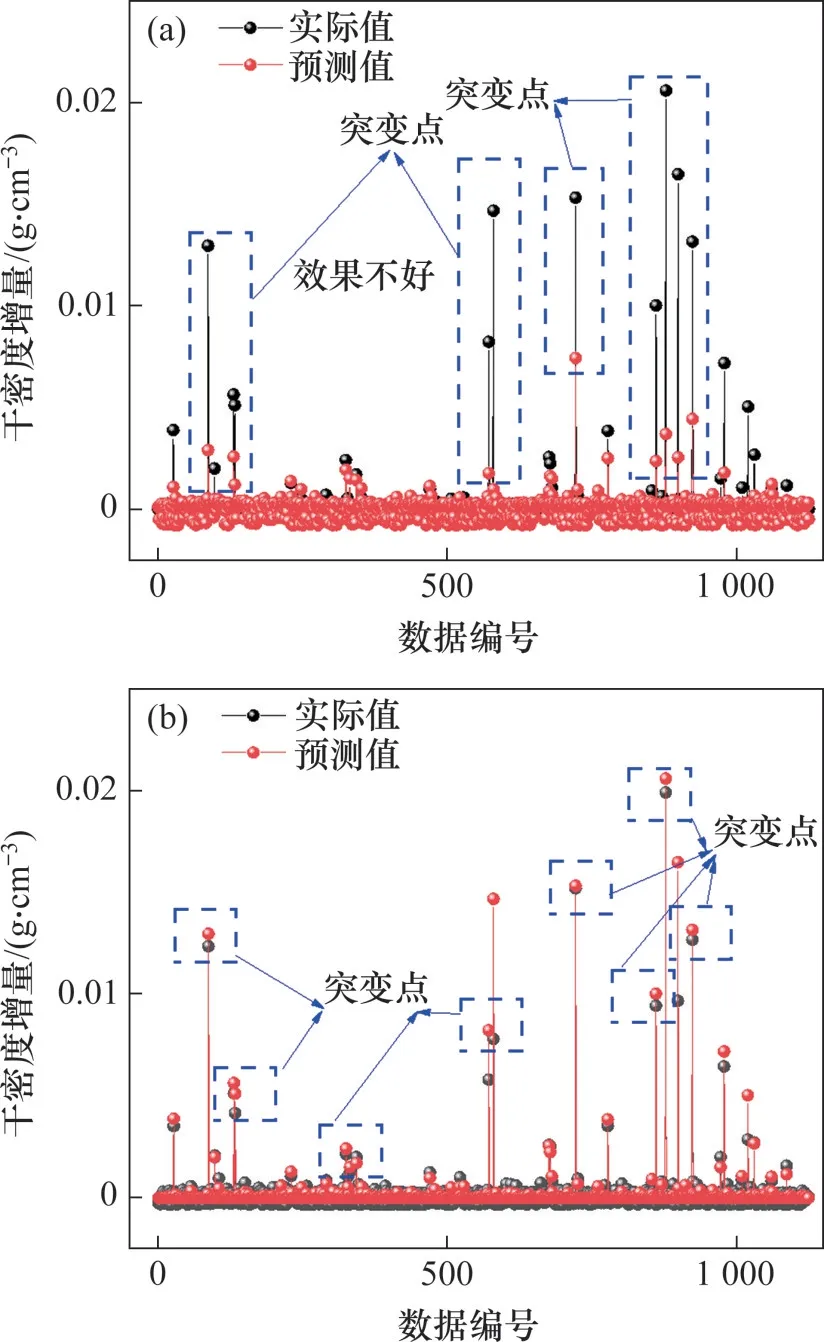
圖9 兩類模型干密度增量的實際值和預測值Fig.9 Actual values and predicted values of dry density increments for two types of models

式中：N為預測樣本數量；yt和y′t分別為參數的實際值和預測值。

由圖9 可知：傳統BP 神經網絡模型可以較好預測到絕大部分數據，但是對于某些干密度增量突出點預測效果不好；而改進的BP神經網絡模型具有較強的預測能力，對干密度增量的起伏趨勢都能很好地進行預測。改進的BP神經網絡模型計算的MSE和MAE分別為4.5×10-6和1.4×10-3，而傳統的BP 神經網絡模型計算的MSE和MAE分別為6.35×10-4和5.1×10-3。因此，改進的BP神經網絡模型不僅在訓練集和測試集上表現優異，而且在測試集上的預測精度高，泛化能力強，能夠很好地適用于干密度增量的預測。在后面的動態優化過程中，采用改進的BP神經網絡進行干密度增量預測。

4.2 壓實質量動態優化結果

振動壓實過程的優化結果如圖10所示。從圖10(a)可見：優化后，振動頻率隨著振動壓實過程由最初的10 Hz 逐漸增大到27 Hz，這一優化結果符合現有“最優頻率會隨著土體剛度增加而增加”的認識[25]，證明了頻率優化方案的可行性。同時，優化后，振動振幅隨著振動壓實過程先從0.15 mm開始逐漸增大，到連續振動120次時，振幅變化逐漸穩定，最終為0.34 mm。這是因為振動振幅為控制激振荷載及激振強度的重要因素，隨著土體壓密，需要更大的激振荷載來克服顆粒間的動摩擦力，使得顆粒發生相對位移[26-27]，因此，選擇逐步增大的振幅調整方案進行壓實是可行的。從圖10(b)可見：改進后的能量輸出在整個壓實過程中皆小于改進前的能量輸出，并且最終有效減小了能量127.58 J，占改進前能量輸出的25.61%。

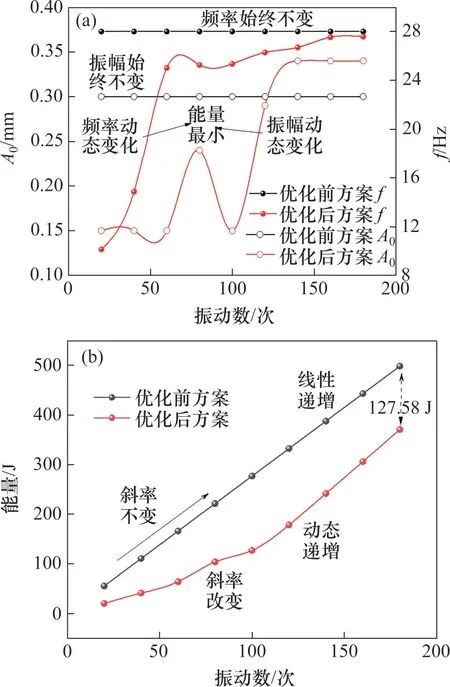
圖10 優化前后試驗方案下的振幅和能量演化Fig.10 Evolution of amplitude and energy under preoptimized and post-optimized tests schemes

綜上可得，基于GA算法的動態優化方法能根據當前土體密實狀態選擇合適的振動參數，且在保證95%壓實度的前提下能夠有效減小振動過程中的能量，有效提升壓實效率，減小對儀器的磨耗。

4.3 壓實質量動態優化對比驗證

為進一步確定優化后振動參數調整結果的準確性，采用改進后的方案進行室內振動壓實試驗。由于振動壓實儀無法連續調幅，需要對振幅的輸出方案進行調整，調整后的振動參數輸出方案如表2所示。采用變頻器對電機轉速進行調節，采用Modbus 通訊協議開發振動壓實儀配套智能控制軟件，實時調節振動參數，實時監控儀器工作狀態，結果如圖11所示。

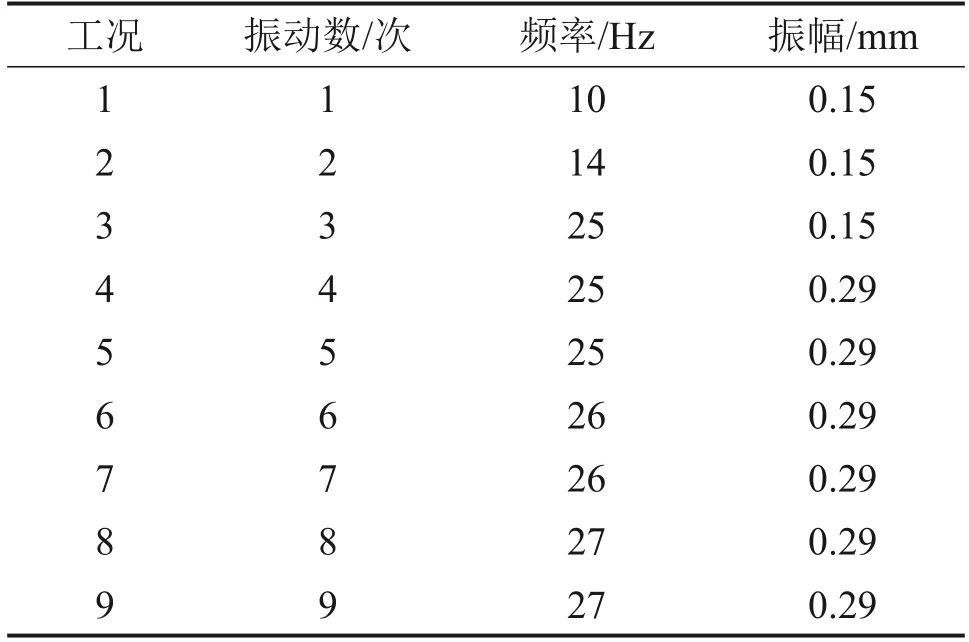
表2 優化后振動壓實試驗參數Table 2 Optimized parameters for vibratory compaction tests

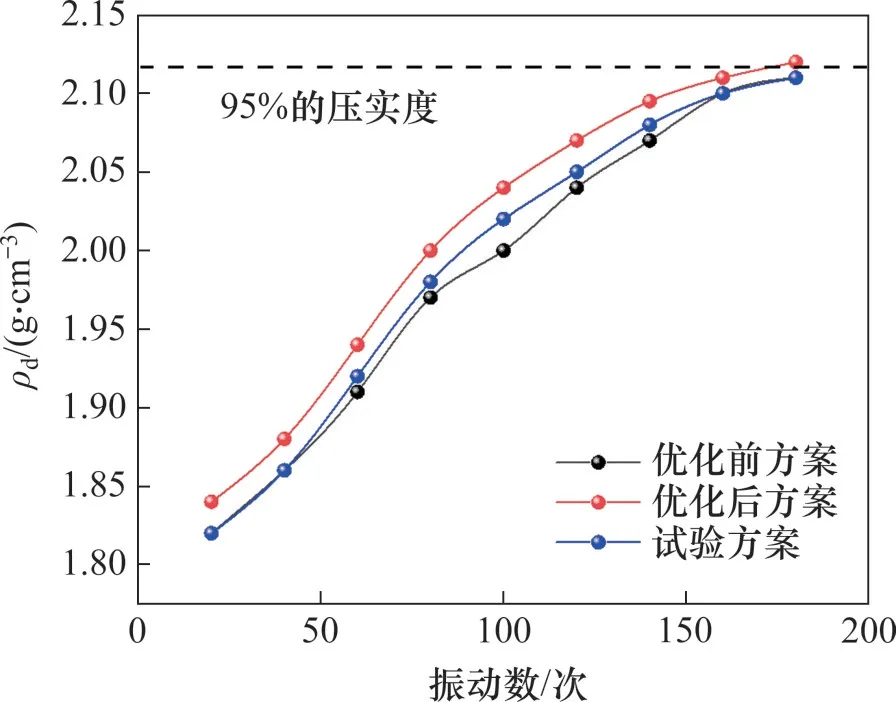
圖11 優化前后試驗方案下的干密度演化Fig.11 Evolution of dry density under pre--optimized and post-optimized test schemes

圖11 展示了優化前后試驗方案下，干密度與振動次數之間的關系。其中，優化后方案的干密度是根據建立的改進BP神經網絡預測得到。從圖11 可以看出：經過180 次連續振動(9 次完整振動)后，這3 種方案均能夠達到壓實度為95%的要求，且3種輸出方案所需要的時間基本一致，整個過程需要12.5 s。統計壓實前后土樣級配，并計算相應的顆粒破碎率，發現采用改進調整后的試驗方案進行壓實的顆粒破碎率為3.2%，小于采用改進前的方案進行壓實的顆粒破碎率(4.1%)。

因此，本文提出的基于改進BP 神經網絡算法和GA的振動參數動態優化方法能夠根據當前土體密實狀態選擇合適的振動參數，使得整個壓實過程中壓實器械輸出的能量最小。

5 結論

1)振動強度存在閾值，使得干密度達到最大值，而進一步增大振動強度，會使得振動壓實儀“跳振”。較大振動荷載會使得填料的破碎加劇，增加設備損耗，嚴重影響設備使用壽命。

2)引入AdamOptimizer 算法改進傳統的BP 神經網絡，建立干密度增量預測模型，有效提高了預測的收斂速度和精度，對于干密度增量突出點預測的適用性好。

3)提出適用于動態優化的GA 算法的模型參數。當種群數量為150，選擇概率為0.9，交叉概率為0.6，變異概率為0.05 時，可有效保證動態優化方法的準確性。

4)經動態優化方法調整后，振動壓實試驗方案能減小振動能量127.58 J，較改進前的方案減少了25.16%，填料破碎率減小了0.9%，證明了方法的合理性。基于動態優化過程中振動頻率和名義振幅的變化規律，建議在振動壓實過程中可逐步增大其數值，以減小振動過程中的能量。