基于BLUE的雷達/紅外異步融合算法研究

盛 琥，汪海兵

（1.中國電子科技集團公司第三十八研究所，安徽合肥 230088；2.國防科技大學電子對抗學院，安徽合肥 230037）

0 引言

多傳感器數據融合是當前研究的熱點。以常見的雷達/紅外數據融合為例，雷達探測距離遠，單次觀測就能定位目標，且具備全天候工作能力，但容易被反輻射武器打擊；紅外傳感器不輻射信號，抗毀性強，測角精度高，但探測范圍小，且無法測距，需要在其他傳感器引導下發現目標。兩種傳感器組網，在中心統一調度下，對目標協同探測，信息融合，可實現優勢互補、協同增效。由于兩種傳感器的觀測模型不同，探測時間不同步，紅外傳感器數據更新率遠高于雷達，因此該組網系統面臨兩個問題:一是如何基于不同傳感器觀測，估計目標狀態，即非線性濾波問題；二是如何保證跟蹤精度和實時性。

傳統非線性方法包括擴展Kalman 濾波（Extended Kalman Filter,EKF）、粒子濾波［1］（Particle Filter,PF）、容積Kalman 濾波［2］（Cubature Kalman Filter,CKF）或無跡Kalman 濾波（Unscented Kalman Filter,UKF）、轉換量測Kalman 濾波［3］（Converted Measurement Kalman Filter,CMKF）等。上述方法中，EKF 計算量最小，但魯棒性差；PF、UKF、CKF精度高，但計算量大，實用性差。CMKF 實現簡單，且兼顧精度和計算量，因此應用較廣。CMKF 中最具代表性的濾波方法是BLUE（Best Linear Unbiased Estimation），相比EKF，它的魯棒性好；相比采樣類濾波方法（CKF、UKF、PF），它的計算量小，因此在實用中受到重視，相關研究較多。其應用從常規目標跟蹤，拓展到多普勒目標跟蹤、只測角目標跟蹤、機動目標跟蹤等方面，在諸多場景得到應用［4-9］。基于以上分析，在雷達/紅外組網系統中,應用基于BLUE的異步融合算法跟蹤目標。

1 基于BLUE的雷達/紅外組網系統

BLUE 濾波是CMKF 中的代表性算法。CMKF將非線性觀測轉換為直角坐標系內的偽線性表達，推導轉換量測統計特性后，在Kalman 濾波架構下完成狀態估計。目前已有嵌套CMKF、基于量測的CMKF、去相關CMKF 和BLUE 等多種算法，在多普勒目標跟蹤、相控陣雷達目標跟蹤中得到驗證。BLUE 濾波相比其他方法，精度高、計算量小，沒有Kalman濾波的諸多限制，因此受到關注。

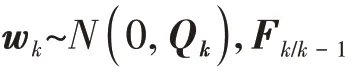
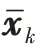
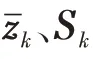
雷達/紅外組網系統以指控中心位置為參考原點，估計目標狀態；中心和傳感器位置不同，各傳感器的錄取時刻和觀測維度也不同，因此雷達和紅外傳感器需要采用不同的BLUE 濾波器，異步融合跟蹤目標，具體步驟如下:

1）基于多幀雷達觀測和目標運動特性，建立多個暫時航跡（可能的目標航跡）。

2）定期檢查暫時航跡，判斷其是否滿足起始條件，滿足條件轉到步驟3，將暫時航跡轉為穩定航跡，否則繼續維護暫時航跡。

3）基于暫時航跡的歷史觀測，粗略估計目標初始狀態，建立航跡。

4）如果雷達錄取的點跡與航跡關聯，采用改進BLUE 濾波器，更新該航跡；如果紅外傳感器錄取的點跡與航跡關聯，采用修正BLUE 濾波器，更新該航跡。

5）定期檢查航跡，如果航跡連續多幀錄取不到點跡，判斷目標消失，刪除該航跡。

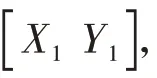
2 改進BLUE濾波算法

雷達觀測為斜距rm,1和方位θm,1，觀測與真值的關系為

當斜距和方位誤差的乘積變大時，基于該模型的BLUE 濾波器性能變差。原因如下:將式（5）展開

方位估計θf,1是方位觀測θm,1和方位預測θp,1的加權和，表達式如下:

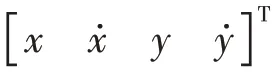
目標真實狀態未知，因此方位預測的方差近似為

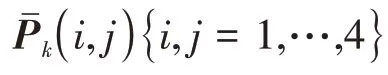
約束1:在垂直雷達視線方向（切向），方位觀測誤差要遠大于方位預測誤差；

約束2:在沿著雷達視線方向（徑向），觀測項誤差要遠大于預測項誤差。

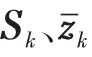
約束2的理由是:公式（8）中，雷達徑向誤差由觀測項誤差（與觀測相關）和預測項誤差（與預測相關）組成。BLUE 濾波器相關參數沒有閉式解（是用位置預測近似得到），通過αk,1調節觀測項誤差在徑向誤差的比重，避免徑向濾波發散。

約束1的數學表達式為

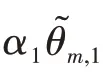
約束2的數學表達式推導如下:

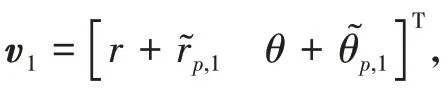
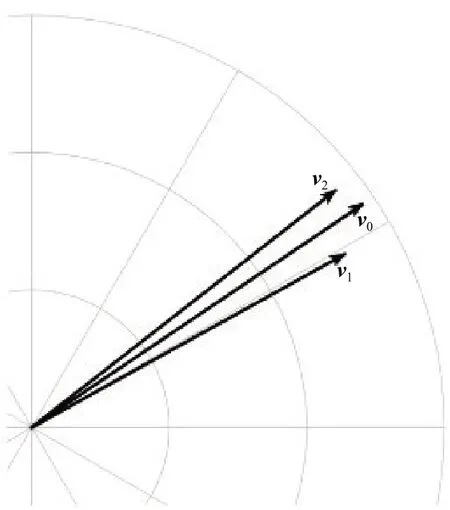
圖1 觀測向量、預測向量和真值向量示意圖

近似時，假設方位預測誤差遠小于方位估計誤差。?的方差為

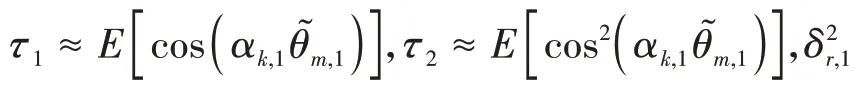
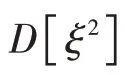
綜合公式（12）和（17）兩重約束，求解出公式（9）中αk,1表達式為

其中，

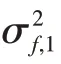
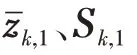
3 修正BLUE濾波算法

紅外傳感器觀測θm,2與真值的關系為

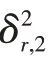
得到rp,2后，構建k時刻轉換量測zk,2，下標2 表示紅外傳感器的轉換量測。

其中，

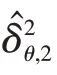
類似改進BLUE 濾波器，通過在紅外傳感器徑向和切向上分別加以約束，可以求解加權系數αk,2。

約束1的數學表達式為

約束2的數學表達式為

αk,2的表達式如下:

其中，

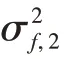
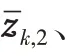
I是2階單位陣，Λk,2定義如下:

其中，

基于以上濾波參數，對目標遞歸濾波，實現純方位的BLUE跟蹤。

4 仿真分析

下面仿真驗證所提方法性能，場景1仿真參數如下:場景包括兩部性能相同的雷達、一部紅外傳感器。雷達斜距誤差σr,1=50 m，方位誤差σθ,1=4°，兩部雷達位于X軸上，相對Y軸對稱放置，間距10 km。紅外傳感器位于坐標原點，方位誤差為σθ,2=2°。目標從正北方向100 km 處向南飛行，速度（0，-50）m/s。飛行過程中，各軸的位置噪聲獨立無關，標準差0.1 m；速度噪聲獨立無關，標準差0.1 m/s。為模擬實際情況，傳感器的觀測時間不同步，而是等間隔交替探測目標，時間間隔T=1 s。蒙特卡洛仿真100 次，仿真時長200 s。將本文所提方法與經典BLUE 融合方法對比，二者區別是:當雷達探測到目標時，本文融合方法采用改進BLUE 濾波，經典融合方法使用文獻［6］的BLUE 濾波；當紅外傳感器探測到目標時，本文融合方法采用修正BLUE 濾波，經典融合方法采用文獻［17］的只測角BLUE 方法。兩種融合方法都采取兩點估計法來初始化目標狀態，修正BLUE 和改進BLUE的放大倍數都設置為κ=6。對比的性能參數包括位置估計精度（RMSE）和歸一化估計誤差均方（ANEES），前者表征濾波精度，后者衡量濾波誤差和實際誤差的匹配程度，ANEES 為1 時，濾波一致性最好，估計置信度最高。仿真結果如圖2所示。

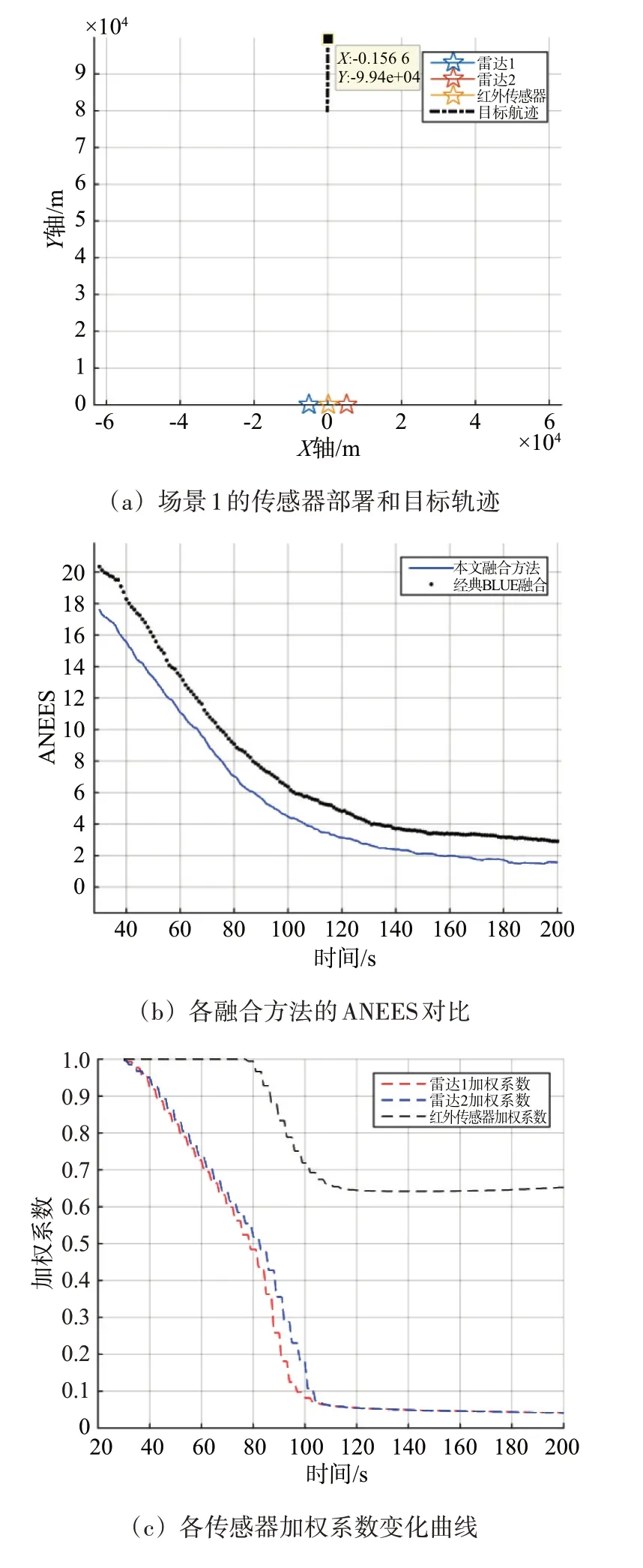
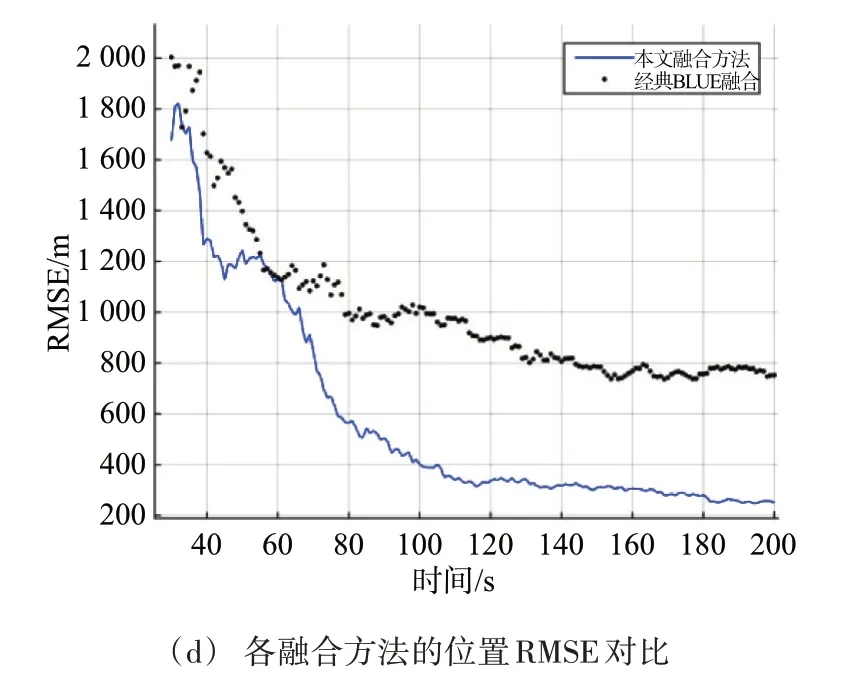
圖2 場景1的跟蹤性能對比

兩種方法的初始跟蹤性能接近，在跟蹤穩定后（30 s 后），所提融合方法的ANEES 比經典BLUE融合更逼近1，也即濾波置信度更好，如圖2（b）所示。由圖2（c）可見，30 s 后，雷達加權系數小于1；80 s后，紅外加權系數小于1，此時方位估計誤差小于方位觀測誤差，所提融合方法的精度明顯優于經典BLUE 融合，紅外傳感器的加權系數最終穩定在0.65，雷達加權系數穩定在0.05。所提方法位置融合精度（300 m）比經典BLUE 方法（800 m）提高2倍多，如圖2（d）所示。

為評估所提方法在不同布局下的性能，場景2中，其他條件不變，將兩部雷達間距由10 km 擴大到60 km。仿真結果如圖3所示。

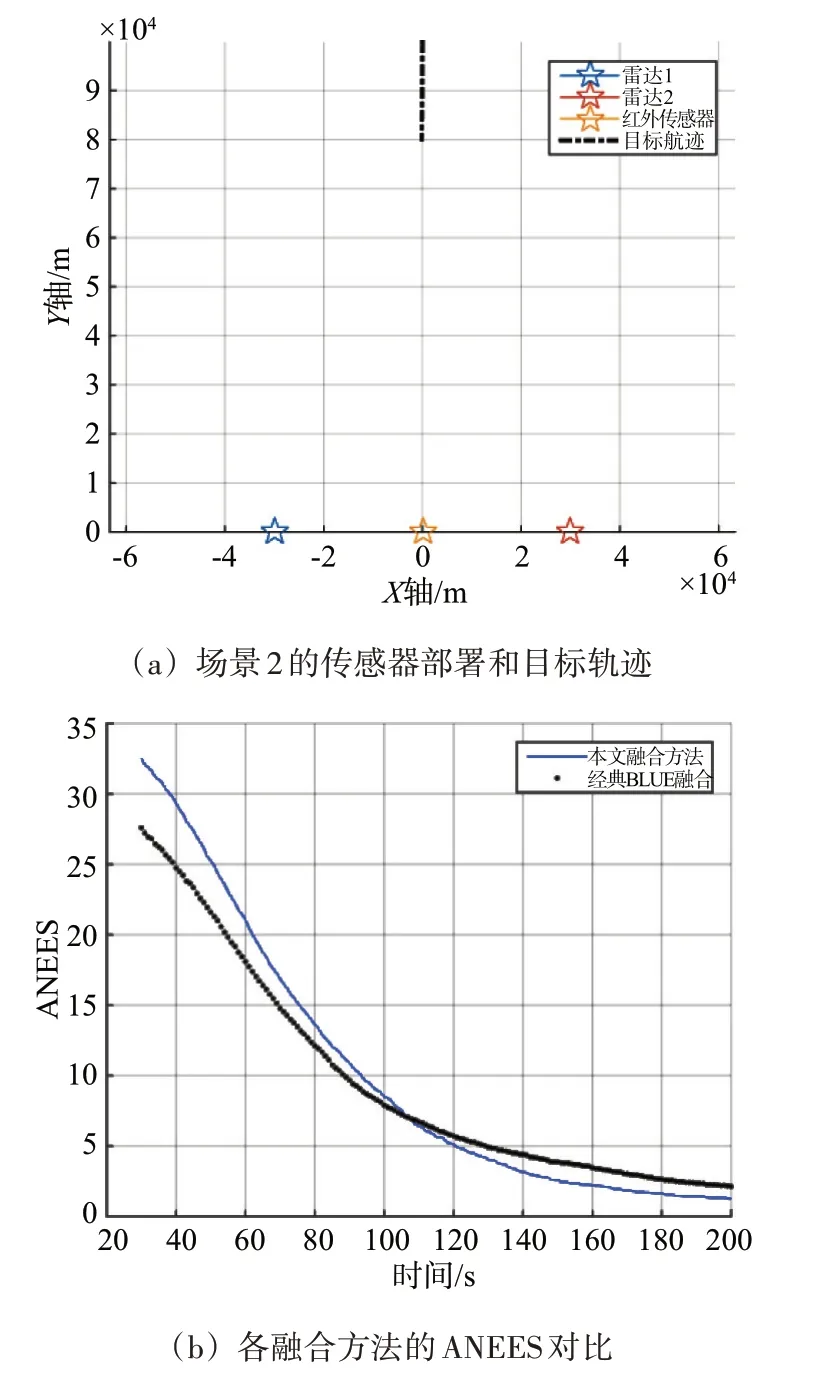
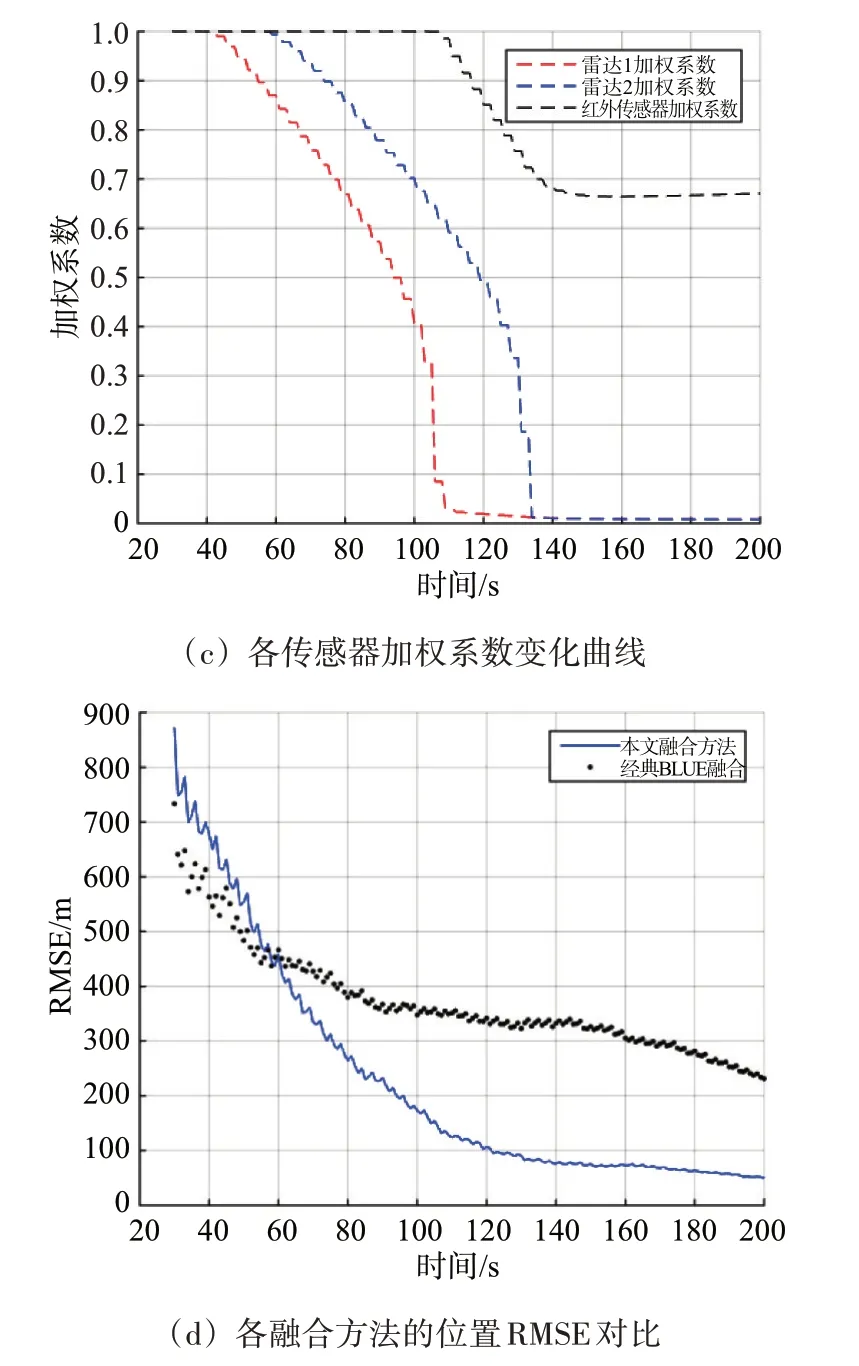
圖3 場景2的跟蹤性能對比

跟蹤穩定后，兩種方法的ANEES 變化情況類似，如圖3（b）所示。在圖3（c）中，紅外傳感器的加權系數約為0.65，雷達加權系數逼近0。幾何布局的改善和方位估計精度的提高，使得所提方法的融合精度（50 m）比經典BLUE 方法（250 m）提高5倍，如圖3（d）所示。

融合方法在兩種仿真場景中的運行時間如表1所示。

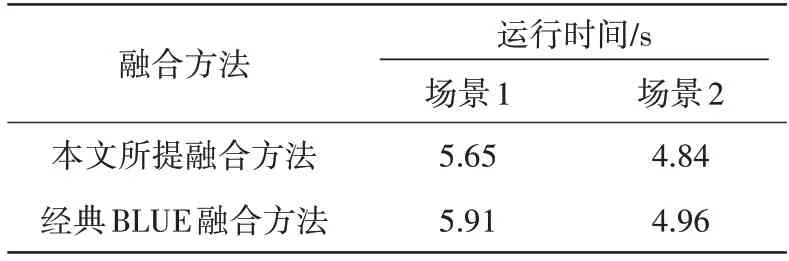
表1 各融合方法迭代運行時間對比（100次）

由表1結果可見，所提方法計算量略大于經典BLUE 方法，主要時間消耗在估計各傳感器的加權系數上，相對于融合精度數量級的提升，這點時間開銷可以承受。綜上可見，基于BLUE的異步融合跟蹤方法，可以用于雷達/紅外傳感器組網系統，在精度、置信度和計算量上具有優勢，有較高的應用價值。

5 結束語

針對雷達/紅外傳感器組網，異步融合跟蹤目標的問題，提出一種基于BLUE 的融合跟蹤方法。在雷達跟蹤目標時，采用改進的轉換量測模型，提高估計精度；在紅外傳感器跟蹤目標時，采用修正的轉換量測模型，實現純方位目標跟蹤。理論分析和仿真實驗證明:所提融合方法將估計精度提高2～5倍，實時性和魯棒性都有所保證。其設計思想對其他多源信息融合的應用具有借鑒意義。