基于梯次啟動(dòng)與優(yōu)化算法的多集群風(fēng)機(jī)最優(yōu)調(diào)頻方法

陳汝斯,李大虎,周泓宇,周悅,饒渝澤,姚偉

(1. 國(guó)網(wǎng)湖北省電力有限公司電力科學(xué)研究院,武漢市 430077;2. 國(guó)網(wǎng)湖北省電力有限公司,武漢市430077;3. 強(qiáng)電磁工程與新技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室(華中科技大學(xué)),武漢市 430074)

0 引 言

隨著工業(yè)的迅猛發(fā)展,化石能源被不斷開(kāi)采利用,其全球儲(chǔ)量逐年下降[1],面臨逐漸枯竭的危機(jī)[2]。可再生能源因其可持續(xù)發(fā)展[3]和低污染[4]的特點(diǎn),被認(rèn)為是解決能源短缺和環(huán)境惡化的有效途徑[5]。其中,風(fēng)力發(fā)電因其技術(shù)相對(duì)成熟和市場(chǎng)化程度高等優(yōu)勢(shì)[6],已普遍應(yīng)用于傳統(tǒng)發(fā)電不足領(lǐng)域[7]。

風(fēng)力發(fā)電機(jī)(wind turbines, WT)通過(guò)直流(direct current, DC)輸電并網(wǎng)是一種主要的風(fēng)電消納方式[8],然而WT的轉(zhuǎn)子速度可能會(huì)與系統(tǒng)頻率解耦,難以為電網(wǎng)提供有效的慣性支撐,嚴(yán)重威脅電力系統(tǒng)的安全穩(wěn)定運(yùn)行[9]。其中,雙饋異步發(fā)電機(jī)(doubly-fed induction generator, DFIG)具有運(yùn)行速度范圍廣、體積小、成本低等優(yōu)點(diǎn),已經(jīng)成為當(dāng)前應(yīng)用最廣泛的風(fēng)力發(fā)電機(jī)。但與傳統(tǒng)的同步發(fā)電機(jī)(synchronous generators, SG)相比[10],DFIG無(wú)法及時(shí)對(duì)系統(tǒng)頻率擾動(dòng)做出響應(yīng)。此外,如果風(fēng)電并網(wǎng)帶來(lái)的額外有功功率備用容量?jī)H由傳統(tǒng)機(jī)組提供,那么系統(tǒng)運(yùn)行成本將大大增加,且造成能源浪費(fèi)。綜上所述,研究大規(guī)模風(fēng)電并網(wǎng)的頻率特性和頻率調(diào)節(jié)控制具有重要意義[11]。

近年來(lái),風(fēng)電場(chǎng)(wind farms, WF)開(kāi)發(fā)了多種頻率調(diào)節(jié)控制策略,主要分為儲(chǔ)能控制、卸荷控制、轉(zhuǎn)子轉(zhuǎn)速控制和下垂控制等[12]。特別是,文獻(xiàn)[13]和[14]通過(guò)釋放儲(chǔ)能設(shè)備的能量實(shí)現(xiàn)了交流(alternative current, AC)側(cè)的頻率調(diào)節(jié),然而,加入儲(chǔ)能設(shè)備會(huì)提高成本。文獻(xiàn)[15]采用了卸荷控制來(lái)實(shí)現(xiàn)一次頻率調(diào)節(jié),這種控制方法保留了備用電源,但嚴(yán)重阻礙了風(fēng)能的有效利用。文獻(xiàn)[16]運(yùn)用轉(zhuǎn)子轉(zhuǎn)速控制策略提供系統(tǒng)頻率支撐。文獻(xiàn)[17]提出在外環(huán)控制基礎(chǔ)上引入有功功率-頻率下垂特性以實(shí)現(xiàn)頻率調(diào)節(jié)。特別地,下垂控制能夠解決柔性DC系統(tǒng)功率和AC電網(wǎng)頻率之間的耦合問(wèn)題,但其逆變器仍不能提供慣性支撐,不能實(shí)現(xiàn)一次頻率調(diào)節(jié),也不能抑制如SG容量不足造成的負(fù)荷干擾。鑒于下垂控制中存在的主要問(wèn)題,虛擬同步發(fā)電機(jī)技術(shù)應(yīng)運(yùn)而生[18]。文獻(xiàn)[19]將虛擬調(diào)速器引入慣性控制環(huán)節(jié),以提供慣性響應(yīng)并實(shí)現(xiàn)一次調(diào)頻。

風(fēng)電場(chǎng)參與頻率支撐控制策略主要可以分為:轉(zhuǎn)子動(dòng)能控制、功率備用控制[9]。采用轉(zhuǎn)子動(dòng)能控制時(shí),為了最大化利用捕獲的風(fēng)能,風(fēng)電場(chǎng)各風(fēng)機(jī)正常工作時(shí),均采用最大功率點(diǎn)跟蹤方式。在該方式下,風(fēng)電機(jī)組可通過(guò)附加控制響應(yīng)頻率變化參與系統(tǒng)頻率調(diào)節(jié),包括慣性控制和下垂控制。采用轉(zhuǎn)子動(dòng)能控制,風(fēng)機(jī)通過(guò)釋放轉(zhuǎn)子動(dòng)能參與頻率調(diào)節(jié),無(wú)需棄風(fēng)保留備用功率。由于釋放轉(zhuǎn)子動(dòng)能提供調(diào)頻功率,該控制的時(shí)間尺度遠(yuǎn)快于槳距角控制的時(shí)間尺度[20],因此可以認(rèn)為采用轉(zhuǎn)子動(dòng)能控制時(shí),風(fēng)機(jī)槳距角保持不變。盡管采用轉(zhuǎn)子轉(zhuǎn)速控制能夠使工作在最大功率跟蹤方式下的風(fēng)電機(jī)組提供一定的頻率支撐功率,但由于缺少功率備用,支撐時(shí)間和容量有限[21]。因此,可采用減載控制的方法,使風(fēng)電機(jī)組具有和同步發(fā)電機(jī)類(lèi)似的調(diào)頻備用功率。功率備用控制具體可以分為超速減載備用和變槳減載備用兩類(lèi):超速減載是將風(fēng)電機(jī)組工作點(diǎn)從最大功率跟蹤點(diǎn)右移,使風(fēng)機(jī)工作在減載工作點(diǎn)處,此時(shí)風(fēng)機(jī)轉(zhuǎn)速相較于最大功率點(diǎn)跟蹤時(shí)增大,而風(fēng)機(jī)的輸出功率因部分功率備用而小于最大功率;變槳控制則是通過(guò)改變風(fēng)機(jī)槳距角實(shí)現(xiàn)功率備用。

然而,上述研究?jī)H考慮對(duì)電力系統(tǒng)的一次頻率下降(first frequency drop, FFD)進(jìn)行抑制。事實(shí)上,在風(fēng)機(jī)轉(zhuǎn)速恢復(fù)過(guò)程中,二次頻率下降(second frequency drop, SFD)也是不可避免的,且當(dāng)有功功率嚴(yán)重不足時(shí),它比FFD更為嚴(yán)重。因此,文獻(xiàn)[22]開(kāi)發(fā)了一種基于海上WF的兩級(jí)組合控制策略,以提供適當(dāng)?shù)念l率支撐并緩解SFD。然而,上述策略的控制器關(guān)鍵參數(shù)是通過(guò)試錯(cuò)法確定的,難以保證控制精度和穩(wěn)定性,且耗費(fèi)時(shí)間多。

為解決二次頻率跌落、控制參數(shù)選取困難等問(wèn)題,本文開(kāi)發(fā)了一種基于蒲公英優(yōu)化(dandelion optimizer, DO)[23]算法的參數(shù)優(yōu)化策略,對(duì)梯次啟動(dòng)自適應(yīng)慣性下垂控制器的參數(shù)進(jìn)行優(yōu)化,以降低FFD、SFD甚至三次頻率下降(third frequency drop, TFD)。DO算法是一種新提出的啟發(fā)式算法,文獻(xiàn)[23]從準(zhǔn)確性、穩(wěn)定性、收斂性、可擴(kuò)展性等方面證明了DO相較于已有的啟發(fā)式算法具有更優(yōu)異的性能。此外,本文的主要貢獻(xiàn)可歸納為以下兩點(diǎn):

1)運(yùn)用梯次啟動(dòng)策略調(diào)整控制WF,即每個(gè)WF被分為集群1和集群2,分別在負(fù)荷變化和轉(zhuǎn)子角速度恢復(fù)時(shí)進(jìn)行頻率調(diào)節(jié),在保證對(duì)一次頻率下降支撐效果的同時(shí),有效緩解二次頻率跌落。

2)采用自適應(yīng)慣性下垂控制方案,基于DO優(yōu)化算法調(diào)整所設(shè)計(jì)控制器的8個(gè)未知參數(shù),建立柔性直流系統(tǒng)功率與電網(wǎng)頻率之間的關(guān)系,顯著增強(qiáng)系統(tǒng)慣性,提升頻率支撐能力。

1 建模與控制方案

1.1 風(fēng)力渦輪機(jī)建模

根據(jù)空氣動(dòng)力學(xué)原理[24],風(fēng)輪的功率可以表示為:

(1)

式中:ρ、S以及v分別代表空氣密度、WT葉片掃過(guò)的面積、風(fēng)速;R為WT葉片的半徑。

WT的輸出機(jī)械功率為:

(2)

式中:λ和θ分別為葉尖速比和WT的槳距角;ω為WT的轉(zhuǎn)子角速度,rad/s;Cp(λ,θ)為風(fēng)能利用系數(shù),具體表達(dá)式詳見(jiàn)文獻(xiàn)[25]。需要指出的是,本文僅考慮風(fēng)電機(jī)組參與系統(tǒng)慣性和一次調(diào)頻過(guò)程,時(shí)間尺度為10 s左右,因此在這一暫態(tài)過(guò)程中,可認(rèn)為風(fēng)速不變,風(fēng)機(jī)出力大小不變。

由文獻(xiàn)[25]可知,WT的風(fēng)能利用系數(shù)Cp由λ和θ決定,其關(guān)系如圖1所示。由圖1可以看出,在一定的槳距角下,隨著葉尖速比的增大,風(fēng)能利用系數(shù)先增大后減小。最大風(fēng)能利用系數(shù)隨槳距角的增大而減小。因此,通過(guò)控制WT在不同風(fēng)速下的槳距角,可以獲得最大的功率輸出。此外,為了獲取最大功率輸出,WT的槳距角θ保持為0°,本文將額定風(fēng)速設(shè)定為12 m/s。

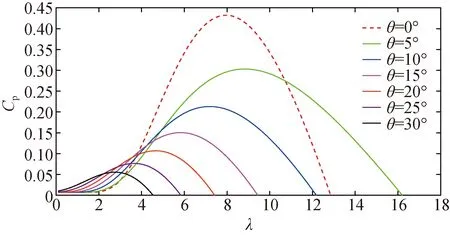
圖1 不同槳距角下風(fēng)能利用系數(shù)與葉尖速比的關(guān)系

當(dāng)風(fēng)機(jī)參數(shù)固定后,對(duì)于特定的一臺(tái)風(fēng)機(jī),當(dāng)風(fēng)速一定時(shí)(即風(fēng)輪面功率一定時(shí)),其風(fēng)能利用系數(shù)與其風(fēng)機(jī)轉(zhuǎn)速相關(guān)(風(fēng)機(jī)輸入機(jī)械功率=風(fēng)輪面功率×風(fēng)能利用系數(shù))。不同風(fēng)速下,風(fēng)機(jī)的最大輸出功率均滿(mǎn)足:Pe=koptωr3,其中kopt是與風(fēng)力機(jī)葉片面積、風(fēng)輪半徑、空氣密度等相關(guān)的常數(shù),ωr為轉(zhuǎn)子轉(zhuǎn)速。

1.2 梯次啟動(dòng)自適應(yīng)慣性下垂控制方案

如圖2所示,測(cè)試系統(tǒng)采用了基于WF和AC系統(tǒng)的三區(qū)四端多端高壓直流測(cè)試系統(tǒng)(VSC-multi-terminal high voltage direct current system, VSC-MT-HVDCS),該系統(tǒng)包括兩個(gè)WF、一個(gè)VSC-MT-HVDCS和一個(gè)AC系統(tǒng)[26]。其中,每個(gè)WF包括5個(gè)等效WT,它們一起向AC系統(tǒng)傳輸電能。在本文中,WF1中WT1—WT5的轉(zhuǎn)子角速度依次確定為0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, 1.05 pu。此外,WT6—WT10的轉(zhuǎn)子角速度也依次確定為0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, 1.05 pu。注意,只有WF1的WT在頻率事件發(fā)生,即負(fù)荷增加后,才通過(guò)梯次啟動(dòng)自適應(yīng)慣性下垂控制方案參與頻率支撐,而WF2的所有WT均在最大功率點(diǎn)(maximum power point, MPP)狀態(tài)下運(yùn)行。同時(shí),WF1中的WT根據(jù)其轉(zhuǎn)子角速度按一定比例分類(lèi)為不同的集群。例如,在負(fù)荷增加時(shí),WT2、WT4和WT5屬于集群1,而若集群分類(lèi)比為3∶2,則集群2涉及WT1和WT3。相反,在負(fù)荷減少時(shí),WT1—WT3被分類(lèi)為集群1,若分類(lèi)比也是3∶2,則WT4和WT5被分類(lèi)為集群2。需要指出的是,由于多端柔性直流的解耦作用,在考慮頻率信號(hào)在多個(gè)交流系統(tǒng)之間傳遞時(shí),本文直接采用特定通信線(xiàn)路進(jìn)行頻率傳遞,延時(shí)主要包括了信號(hào)在發(fā)送端的調(diào)制延時(shí),信號(hào)傳輸延時(shí),信號(hào)在接收端的解調(diào)制延時(shí)。由于在光纖通信中,信號(hào)傳輸速度接近光速,信號(hào)傳輸延時(shí)較低,但是信號(hào)調(diào)制和解調(diào)延時(shí)較長(zhǎng)。因此,在仿真中考慮了200 ms的信號(hào)傳遞延時(shí)。

當(dāng)風(fēng)機(jī)穩(wěn)定運(yùn)行在MPPT模式下時(shí),風(fēng)機(jī)輸入的機(jī)械功率已經(jīng)是該風(fēng)速下對(duì)應(yīng)的最大值,因此當(dāng)事故發(fā)生時(shí),風(fēng)機(jī)只能通過(guò)附加控制(包括模仿常規(guī)同步機(jī)的慣性控制和下垂控制)釋放轉(zhuǎn)子動(dòng)能,向上調(diào)頻時(shí)降低轉(zhuǎn)速,暫時(shí)性(風(fēng)機(jī)轉(zhuǎn)速具有安全限值)對(duì)系統(tǒng)提供頻率支撐的電磁能。

風(fēng)機(jī)的轉(zhuǎn)子運(yùn)動(dòng)方程如下所示:

(3)

式中:Pm為輸入風(fēng)機(jī)機(jī)械功率;ΔP(t)表示風(fēng)機(jī)頻率支撐控制中的附加功率值,包含下垂控制部分和慣性控制部分;Tw表示風(fēng)機(jī)轉(zhuǎn)動(dòng)慣量。

對(duì)式(3)兩側(cè)積分可得:

(4)

式中:ωr0代表風(fēng)機(jī)調(diào)頻前的初始轉(zhuǎn)速。

風(fēng)機(jī)轉(zhuǎn)子動(dòng)能如下:

(5)

由式(4)、(5)可知,風(fēng)機(jī)提供頻率支撐的本質(zhì)是犧牲風(fēng)機(jī)的轉(zhuǎn)子動(dòng)能換取輸入系統(tǒng)的電磁能。綜上,風(fēng)電機(jī)組參與系統(tǒng)向上頻率調(diào)節(jié)時(shí),將退出MPPT模式,風(fēng)機(jī)轉(zhuǎn)速下降釋放轉(zhuǎn)子動(dòng)能,從而輸出功率增加,提供頻率支撐功率。

WT的有功功率參考值Pref,i主要由三部分組成,即該WT實(shí)時(shí)轉(zhuǎn)子角速度ωi下的最大功率點(diǎn)(maximum power point,MPP)、慣性控制和下垂控制,如圖3所示。將頻率下垂控制和虛擬慣性控制附加在風(fēng)電機(jī)組的最大功率跟蹤控制環(huán)節(jié)上,風(fēng)電機(jī)組在交流系統(tǒng)發(fā)生負(fù)荷擾動(dòng)期間能夠通過(guò)釋放轉(zhuǎn)子動(dòng)能增發(fā)功率,提供主動(dòng)頻率支撐。風(fēng)機(jī)功率轉(zhuǎn)速曲線(xiàn)如圖4所示,當(dāng)事故未發(fā)生時(shí),其工作點(diǎn)在PMPPT處。當(dāng)故障發(fā)生后,風(fēng)機(jī)轉(zhuǎn)速下降釋放轉(zhuǎn)子動(dòng)能ΔE,風(fēng)機(jī)輸出電磁功率增加,提供頻率支撐功率。此時(shí),風(fēng)機(jī)功率將暫時(shí)高于MPPT的功率值,其工作點(diǎn)由PMPPT轉(zhuǎn)移到Pop1。由于風(fēng)機(jī)在以上頻率支撐過(guò)程中通過(guò)暫時(shí)釋放轉(zhuǎn)子動(dòng)能換取輸入系統(tǒng)的電磁能,其轉(zhuǎn)速下降,而風(fēng)機(jī)具有安全轉(zhuǎn)速范圍,因此風(fēng)機(jī)在該階段后需要進(jìn)行轉(zhuǎn)速恢復(fù)。轉(zhuǎn)速恢復(fù)的過(guò)程可以通過(guò)風(fēng)機(jī)工作點(diǎn)由Pop1到Pop2簡(jiǎn)單描述,與上一階段相反,該階段需降低輸出電磁功率重新恢復(fù)轉(zhuǎn)子動(dòng)能,該階段對(duì)系統(tǒng)產(chǎn)生的功率缺額需通過(guò)適當(dāng)?shù)霓D(zhuǎn)速恢復(fù)策略減緩,否則將引起二次頻率跌落問(wèn)題。

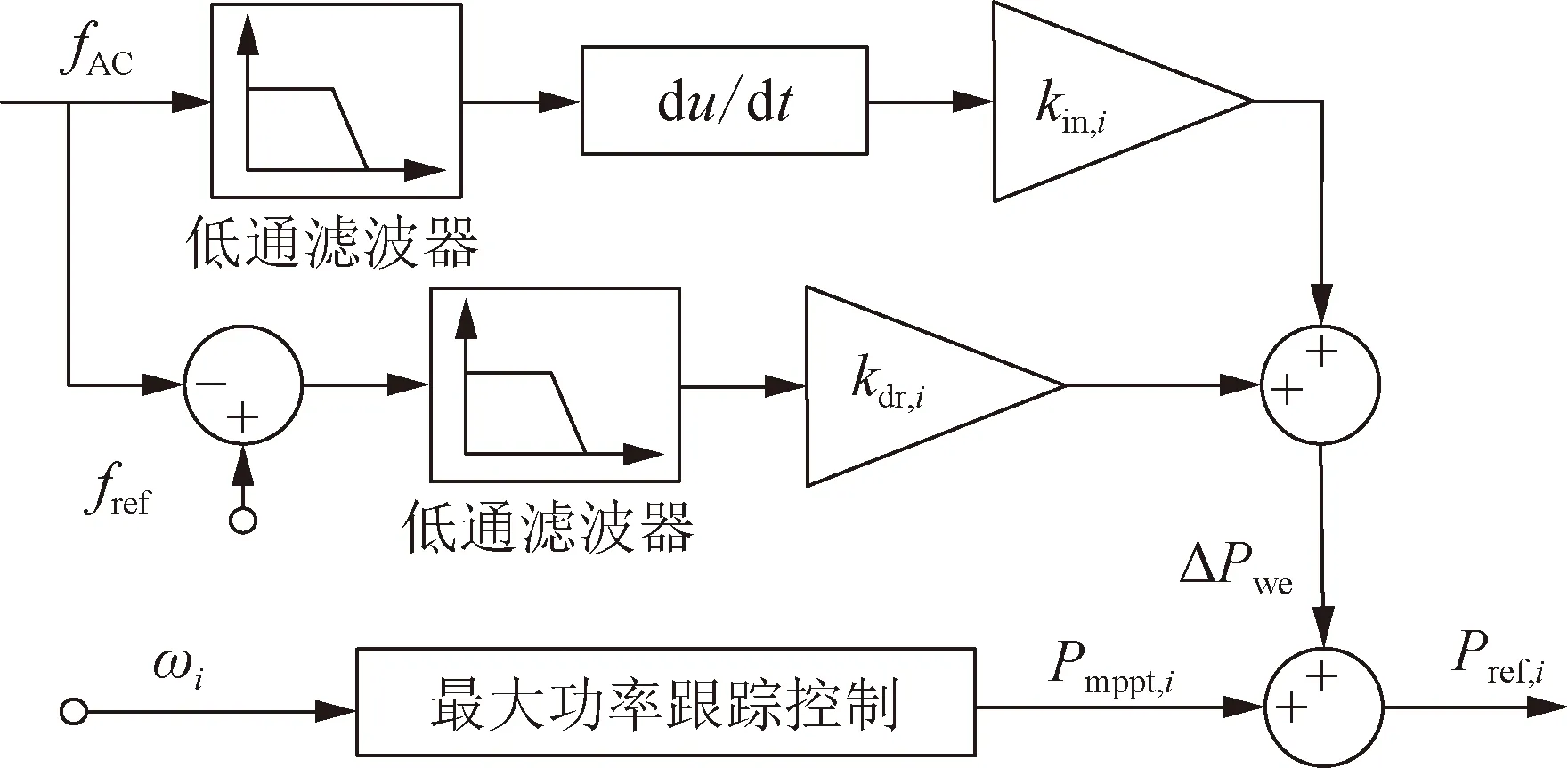
圖3 風(fēng)電機(jī)組綜合慣性控制

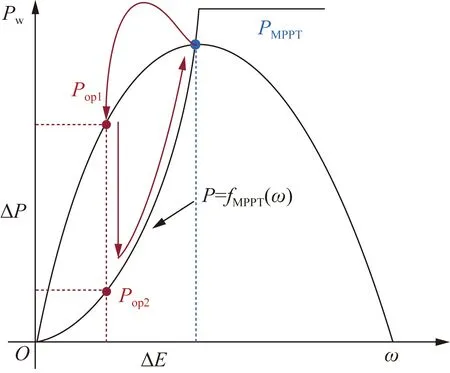
圖4 風(fēng)電機(jī)組功率-轉(zhuǎn)速曲線(xiàn)

對(duì)于第i個(gè)WT,梯次啟動(dòng)自適應(yīng)慣性下垂控制方案如圖5所示。WT經(jīng)過(guò)一定延時(shí)Δt后與另一集群的WT進(jìn)行匹配。也就是說(shuō),利用集群1和集群2分別按一定的順序支撐系統(tǒng)頻率。同時(shí),慣性控制系數(shù)和下垂控制系數(shù)均隨ωi自適應(yīng)變化,具體可描述為:

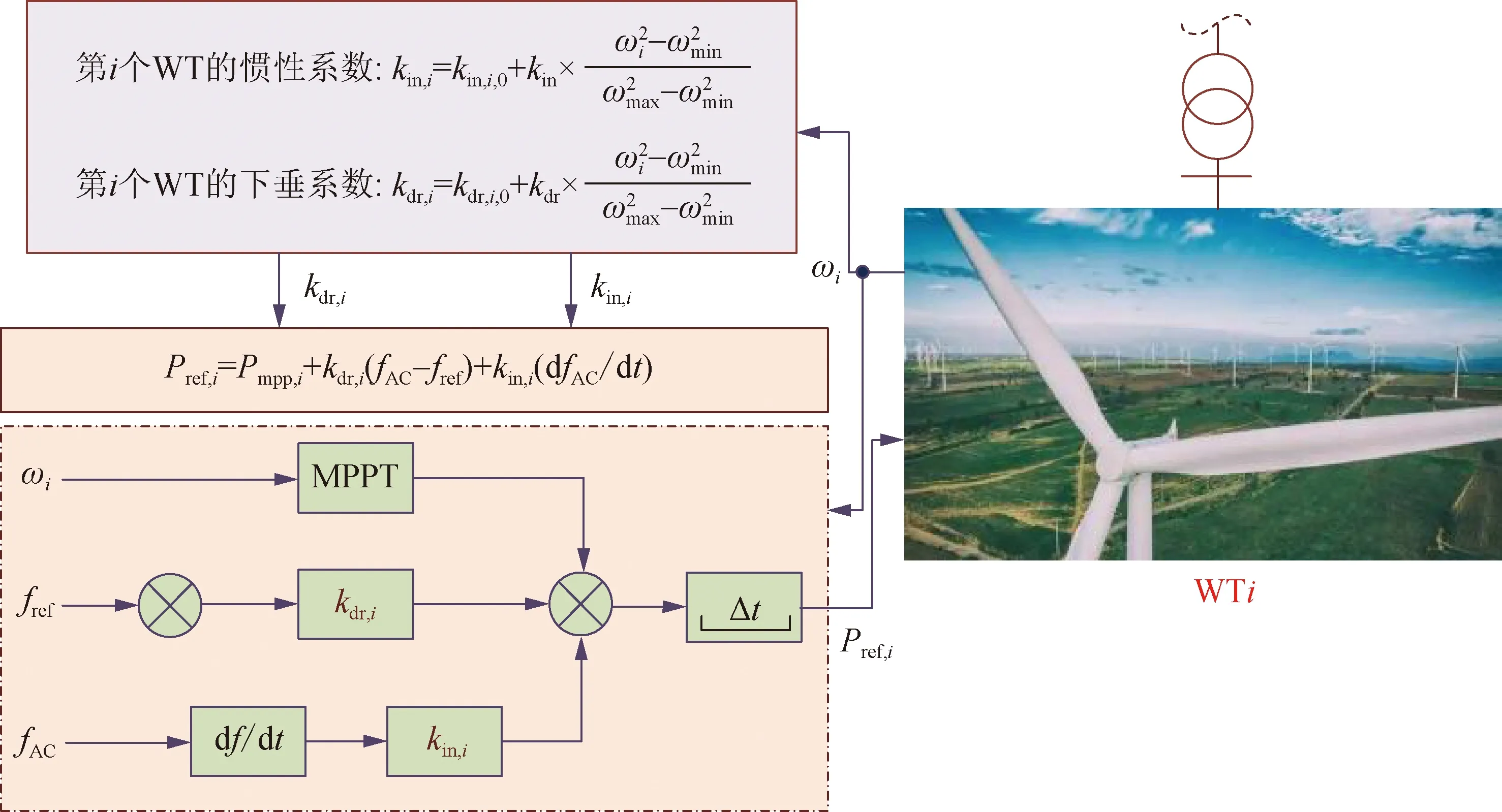
圖5 第i個(gè)WT的梯次啟動(dòng)自適應(yīng)慣性下垂控制方案

(6)

(7)

式中:kin,i,0為慣性控制系數(shù)初始值;kdr,i,0為下垂控制系數(shù)初始值;ωi為第i個(gè)WT的轉(zhuǎn)子角速度;ωmin和ωmax分別為WT的最小和最大轉(zhuǎn)子角速度;kin為慣性系數(shù);kdr為下垂系數(shù)。由于ωmin和ωmax的限制風(fēng)機(jī)的慣性下垂系數(shù)并不會(huì)無(wú)限制地增大。以風(fēng)機(jī)釋放轉(zhuǎn)子動(dòng)能參與調(diào)頻為例,在這一過(guò)程中,風(fēng)機(jī)轉(zhuǎn)子轉(zhuǎn)速ωi減小,逐漸逼近安全范圍最低值ωmin,此時(shí)風(fēng)機(jī)的自適應(yīng)慣性下垂系數(shù)kin,i和kdr,i將逐漸減小逼近kin,i,0和kdr,i,0。因此,只要設(shè)計(jì)合理的初始值kin,i,0和kdr,i,0,就可以保證在參數(shù)自適應(yīng)變化過(guò)程中,風(fēng)機(jī)慣性下垂系數(shù)kin,i和kdr,i始終保持在合理范圍內(nèi)。

WT的輸出功率參考值為:

(8)

式中:fAC為AC系統(tǒng)頻率;fref為系統(tǒng)頻率參考值;Pmpp,i為WT的MPPT參考值。本文在VSC1中進(jìn)行測(cè)試,設(shè)定fref=50 Hz,ωmin=0.70 pu,ωmax=1.20 pu[6]。

與采用常系數(shù)的傳統(tǒng)下垂控制方法相比,自適應(yīng)慣性下垂控制系數(shù)隨WT的實(shí)時(shí)轉(zhuǎn)子角速度ωi變化,不僅能保證轉(zhuǎn)子在安全條件下運(yùn)行,而且能提高風(fēng)能的利用效率,更能及時(shí)調(diào)整WT的狀態(tài)。此外,AC系統(tǒng)頻率fAC的變化率被用作慣性控制的輸入信號(hào)。頻率響應(yīng)初級(jí)階段的頻率偏差較小,頻率變化率較大,自適應(yīng)慣性控制可快速提供頻率支撐[27]。采用下垂控制來(lái)模擬SG的一次調(diào)頻,能夠?qū)崿F(xiàn)頻率事件后期的穩(wěn)態(tài)頻率改善。

值得注意的是,可以從文獻(xiàn)[22]中獲得關(guān)于整個(gè)系統(tǒng)的建模參數(shù)和VSC站控制策略的更多信息。

2 基于DO的梯次啟動(dòng)自適應(yīng)慣性下垂控制器的參數(shù)設(shè)計(jì)

2.1 DO的數(shù)學(xué)描述

受蒲公英依靠風(fēng)傳播種子的啟發(fā),文獻(xiàn)[18]提出了一種新穎的DO算法,該算法充分考慮風(fēng)速以及天氣對(duì)蒲公英種子傳播的影響,可概括為三個(gè)階段,上升階段、下降階段以及著陸階段。

為了更高效地實(shí)現(xiàn)種群進(jìn)化,將種群初始化為:

(9)

式中:p表示種群規(guī)模;D為變量維度,每個(gè)候選解都在給定上界(BU)和下界(BL)之間隨機(jī)生成,第i個(gè)個(gè)體Xi描述為:

Xi=rand×(BU-BL)+BL

(10)

式中:rand為[0,1]間的隨機(jī)數(shù),BU和BL如下所示:

BL=[bl1,…,blD]

BU=[bu1,…,buD]

(11)

式中:bli、bui(i=1,…,D)分別為上下邊界候選解。

此外,將適應(yīng)度值最優(yōu)的個(gè)體選為初始精英,即蒲公英種子最適合生長(zhǎng)的位置。初始精英個(gè)體Xelite(以最小值為例)可表示為:

(12)

式中:X{·}代表初始精英個(gè)體值;find代表具有相等值的兩個(gè)索引;f(Xi)代表第i個(gè)個(gè)體的函數(shù)。

在上升階段,受到風(fēng)速、空氣濕度等天氣因素影響,蒲公英種子將會(huì)上升至不同高度。特別地,天氣可以分為晴朗和陰雨兩種情況。

在晴朗情況下,風(fēng)速可以被認(rèn)為具有對(duì)數(shù)正態(tài)分布lnY～N(μ,σ2)規(guī)律。在此基礎(chǔ)上,隨機(jī)數(shù)沿Y-軸分布更為均勻,蒲公英種子能夠被隨機(jī)吹到更遠(yuǎn)的地方。與此同時(shí),蒲公英種子上方旋渦受風(fēng)速影響被不斷調(diào)整,使蒲公英呈螺旋狀上升,可以表示為:

Xt+1=Xt+α×vx×vy×lnY×(Xs-Xt)

(13)

式中:Xt為第t次迭代時(shí)蒲公英種子的位置;α、vx、vy分別為自適應(yīng)參數(shù)、上升方向系數(shù)、下降方向系數(shù);Xs表示迭代期間搜索空間隨機(jī)選擇的位置,其數(shù)學(xué)表達(dá)式為:

Xs=rand(1,D)×(BU-BL)+BL

(14)

式中:rand(1,D)為1行D列的隨機(jī)矩陣。

此外,lnY服從μ=0和σ2=1的對(duì)數(shù)正態(tài)分布,可以描述為:

(15)

式中:y表示標(biāo)準(zhǔn)正態(tài)分布N(0,1)。

自適應(yīng)參數(shù)α用以調(diào)整搜索步長(zhǎng),可表示為:

(16)

式中:T為調(diào)整系數(shù);tt為搜索時(shí)間。

蒲公英因分離旋渦作用而產(chǎn)生的升力系數(shù)可表示為:

(17)

式中:γ為-π和π之間的隨機(jī)數(shù)。

在陰雨情況下,受限于空氣阻力、濕度等天氣因素,蒲公英種子無(wú)法隨風(fēng)適當(dāng)上升。因此,蒲公英種子將在局部領(lǐng)域進(jìn)行搜索,可以描述為:

Xt+1=Xt×k

(18)

式中:k用于調(diào)節(jié)蒲公英種子的局部搜索區(qū)域,并利用式(19)計(jì)算該區(qū)域,表示為:

k=1-rand×q

(19)

(20)

綜上所述,蒲公英上升階段的數(shù)學(xué)表達(dá)式為:

(21)

式中:rand()為不限制范圍的隨機(jī)數(shù)。

在下降階段,以布朗運(yùn)動(dòng)模擬蒲公英種子的運(yùn)動(dòng)軌跡,可以描述為:

Xt+1=Xt-α×βt×(Xmean_t-α×βt×Xt)

(22)

式中:βt表示布朗運(yùn)動(dòng),是標(biāo)準(zhǔn)正態(tài)分布的隨機(jī)數(shù);Xmean_t為種群在第t次迭代的平均位置,其數(shù)學(xué)公式為:

(23)

在著陸階段,算法有望收斂到全局最優(yōu)解,得到的最優(yōu)解是蒲公英種子最容易存活的近似位置,可以表述為:

Xt+1=Xelite+flevy(ε)×α×(Xelite-Xt×δ)

(24)

式中:Xelite表示蒲公英種子在第t次迭代的最佳位置;δ為代表[0,2]間的線(xiàn)性遞增函數(shù);flevy(ε)為飛行函數(shù),可表示為:

(25)

式中:β代表介于0和2間的任意數(shù);s是固定常數(shù),取0.01,w和tr是[0,1]間的隨機(jī)數(shù)。此外,σ的數(shù)學(xué)表達(dá)式為:

(26)

δ計(jì)算表達(dá)式為:

(27)

2.2 基于DO的控制器參數(shù)優(yōu)化

為了獲得最佳的頻率調(diào)節(jié)性能,本節(jié)提出基于DO的梯次啟動(dòng)自適應(yīng)慣性下垂控制器的參數(shù)優(yōu)化策略。一方面,本文主要關(guān)注圖6所示負(fù)荷增加后系統(tǒng)頻率fAC的動(dòng)態(tài)響應(yīng)特性,即FFD、SFD和TFD。其中,fFFD,fSFD和fTFD分別表示FFD、SFD和TFD的最低點(diǎn)。具體而言,在t0處發(fā)生頻率事件后(即對(duì)于集群1的WT,Δt等于0),集群1立即投入運(yùn)行,而當(dāng)集群1的轉(zhuǎn)子角速度在tⅠ處開(kāi)始恢復(fù)時(shí)(即對(duì)于集群2的WT,Δt為0),則啟動(dòng)集群2,風(fēng)機(jī)梯次啟動(dòng)示意圖如圖7所示。

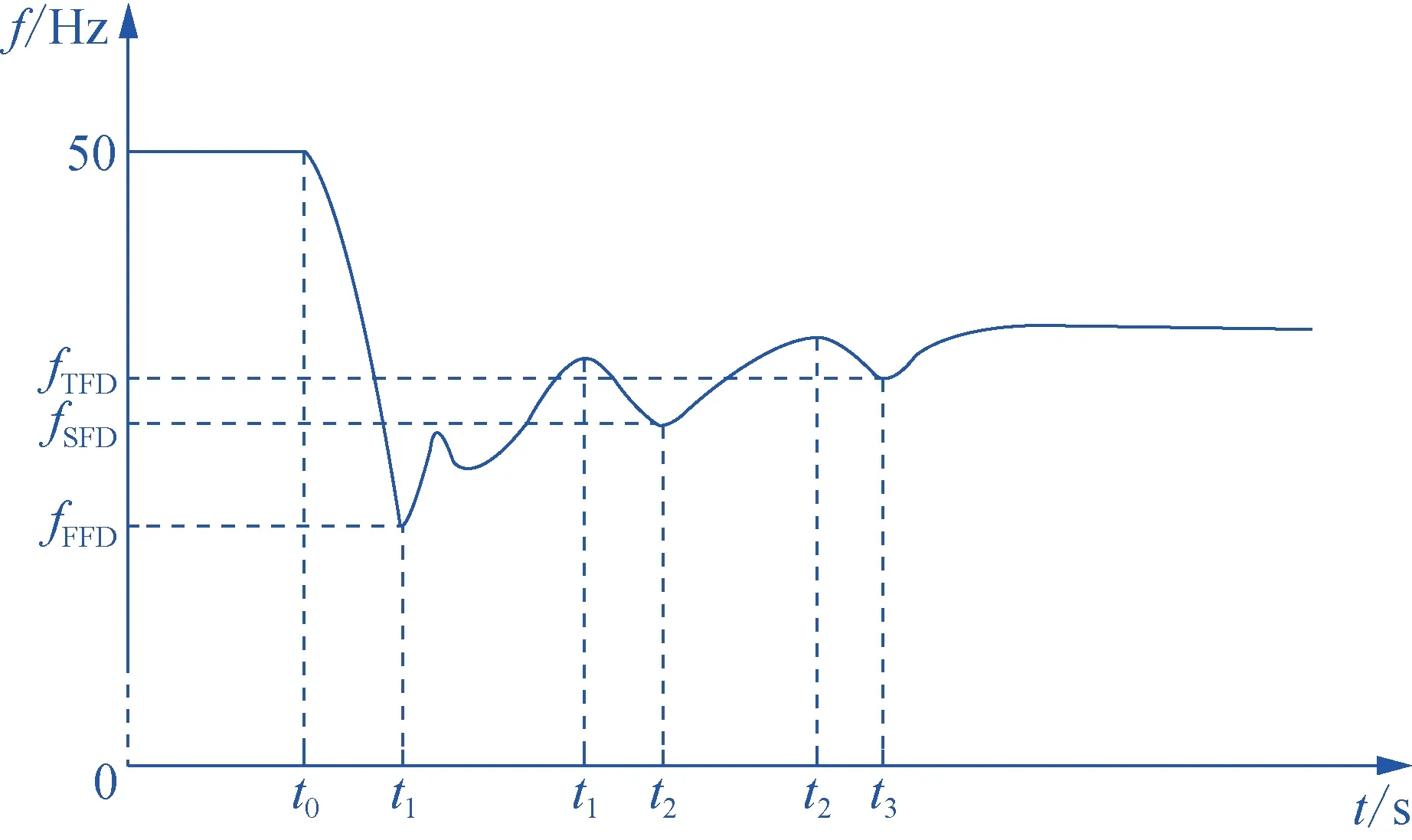
圖6 負(fù)荷增加時(shí)系統(tǒng)頻率的一般動(dòng)態(tài)特性

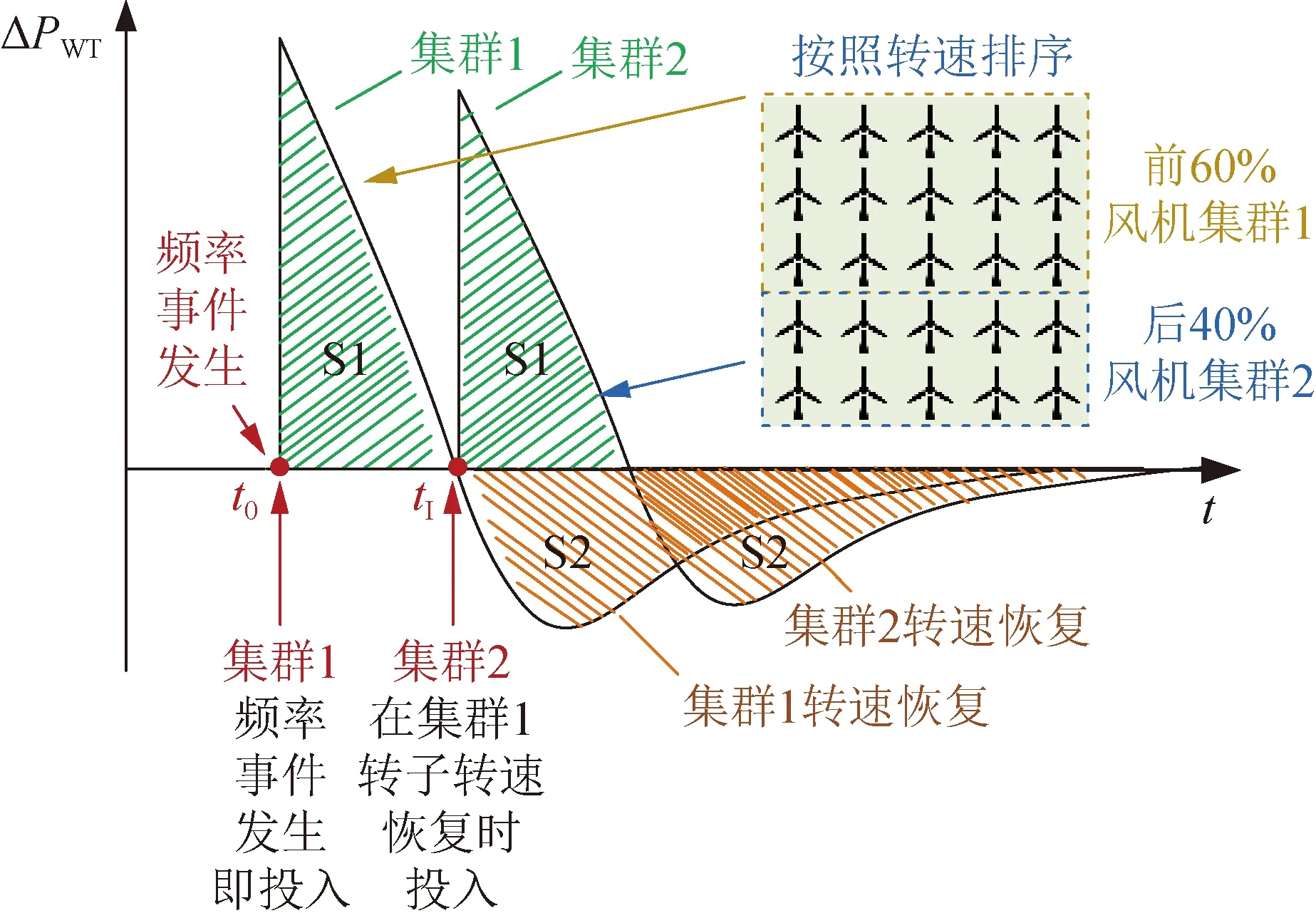
圖7 風(fēng)電機(jī)組梯次啟動(dòng)示意圖

另一方面,還考慮了頻率偏差SIoFD和頻率變化率的積分SIoFVR,這兩者主要體現(xiàn)了系統(tǒng)頻率波動(dòng)的全局信息。其中SIoFD和SIoFVR可以表示為:

(28)

(29)

如式(30)所示,根據(jù)相對(duì)重要性為每個(gè)指標(biāo)分配一個(gè)系數(shù),并將它們相加作為適應(yīng)度函數(shù)。

Ffit=(SIoFD,SIoFVR,fFFD,fSFD,fTFD)=min{AIoFD+AIoFVR+(200fFFD+100fSFD+100fTFD)·50}

(30)

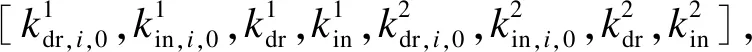
表1 優(yōu)化參數(shù)的范圍

基于DO的梯次啟動(dòng)自適應(yīng)慣性下垂控制器參數(shù)優(yōu)化偽代碼如表2所示。

表2 基于DO算法的控制器參數(shù)優(yōu)化偽碼

3 算例研究

本節(jié)中,在負(fù)荷增加50、100以及150 MW三種情況下,基于DO對(duì)梯次啟動(dòng)自適應(yīng)慣性下垂控制器的參數(shù)進(jìn)行優(yōu)化,以驗(yàn)證和評(píng)估優(yōu)化參數(shù)的有效性。所有案例研究均在MATLAB/Simulink環(huán)境下進(jìn)行,帶可變步長(zhǎng)解算器。此外,種群規(guī)模p和最大迭代次數(shù)Tmax分別設(shè)置為30和200。注意,所有負(fù)荷變化均發(fā)生在第5 s。同時(shí),集群1和集群2分別在負(fù)荷變化和轉(zhuǎn)子角速度恢復(fù)時(shí)參與頻率調(diào)節(jié),即Δt=0 s和Δt=5 s。

表3—5分別給出了在負(fù)荷增加50、100和150 MW時(shí),無(wú)WF參與調(diào)頻、試錯(cuò)法和DO算法得到的最優(yōu)控制參數(shù)。

表3 負(fù)荷增加50 MW情況下不同方法獲得的最佳控制參數(shù)

表4 負(fù)荷增加100 MW情況下不同方法獲得的最佳控制參數(shù)

為了驗(yàn)證基于DO參數(shù)優(yōu)化的控制器在負(fù)荷增加時(shí)的性能,在第5 s時(shí)系統(tǒng)負(fù)荷分別增加50、100和150 MW。該頻率事件中,集群1(即WT2、WT4和WT5)在第5 s立即啟動(dòng),集群2(即WT1和WT3)在第10 s啟動(dòng)。表6為不同方法獲得的FFD、SFD和TFD。圖8詳細(xì)描述了在多種負(fù)荷增加下系統(tǒng)的動(dòng)態(tài)頻率響應(yīng)。從圖8可以看出,與無(wú)WF參與和試錯(cuò)法相比,基于DO優(yōu)化的系統(tǒng)頻率波動(dòng)最小。此外,基于DO優(yōu)化參數(shù)的控制器有效地抑制系統(tǒng)頻率的FFD、SFD和TFD,顯著提高電網(wǎng)的穩(wěn)定性和可靠性。

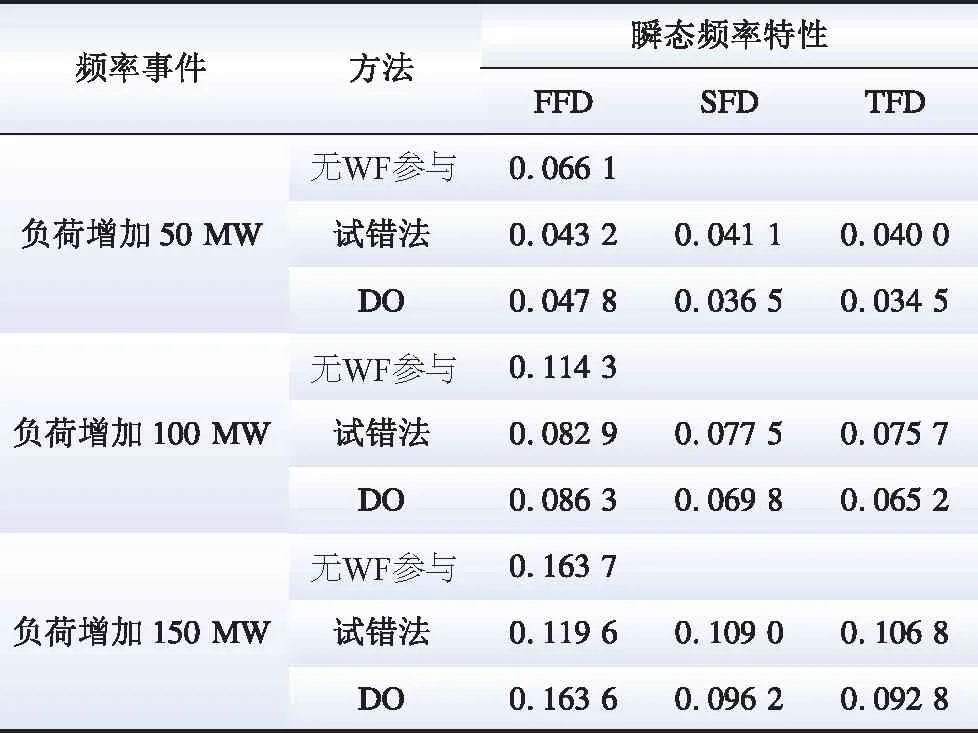
表6 不同方法獲得的FFD、SFD和TFD

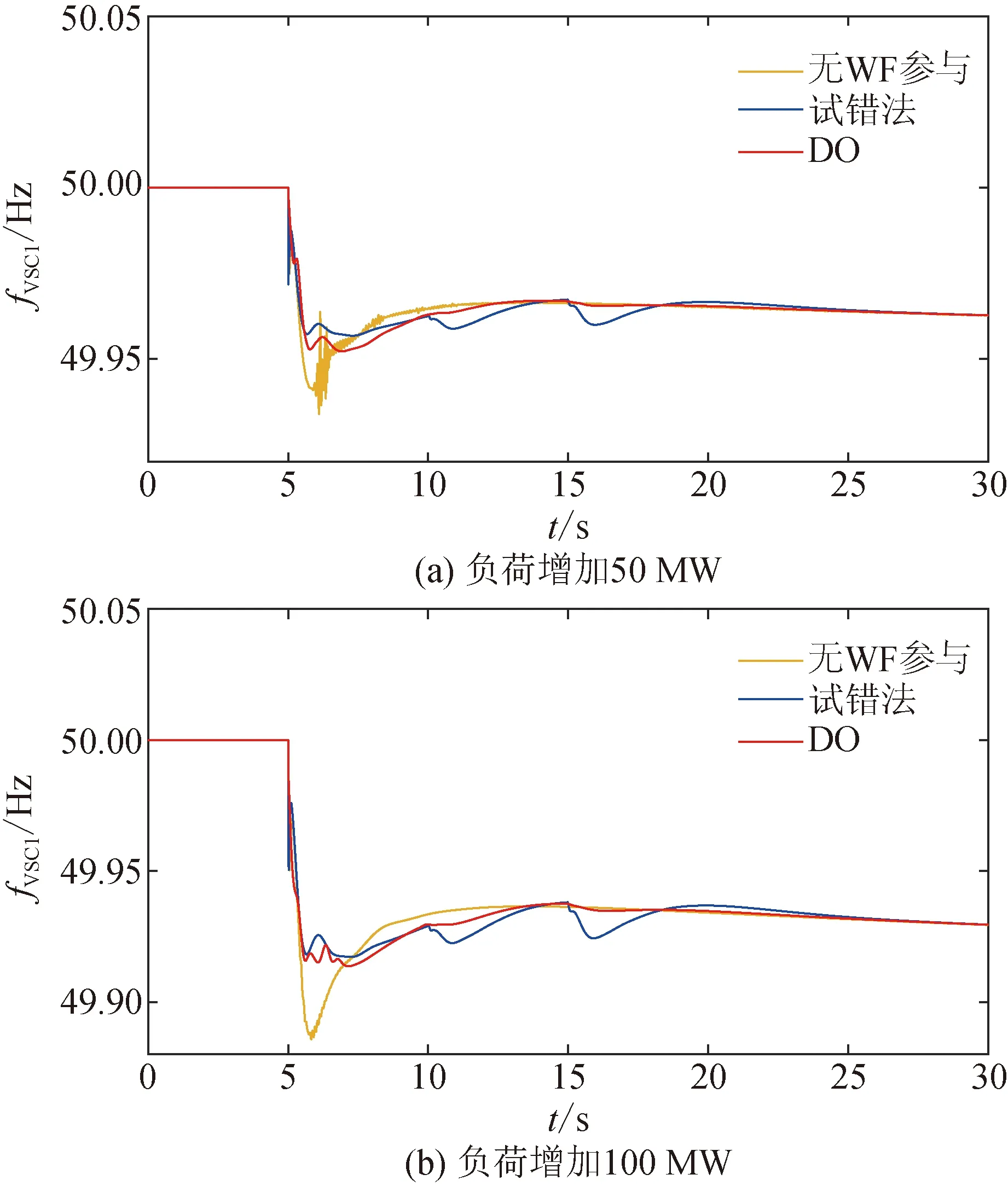
圖8 在各種負(fù)荷增加變化下通過(guò)不同方法獲得的頻率響應(yīng)

在本文所設(shè)仿真環(huán)境下,控制器參數(shù)優(yōu)化過(guò)程所需時(shí)間約為10.9 h。值得注意的是,為更接近實(shí)際電網(wǎng)運(yùn)行場(chǎng)景,在充分考慮多種因素下,該系統(tǒng)模型復(fù)雜,故離線(xiàn)優(yōu)化與控制時(shí)間均較長(zhǎng)。雖然本文針對(duì)三種不同負(fù)荷變化場(chǎng)景分別優(yōu)化了三組不同參數(shù),但在實(shí)際生產(chǎn)中,可根據(jù)具體場(chǎng)景可能出現(xiàn)的最大負(fù)荷波動(dòng)情況離線(xiàn)優(yōu)化出一組參數(shù)作為控制器的最終參數(shù),以滿(mǎn)足在線(xiàn)應(yīng)用的實(shí)際需求。

4 結(jié) 論

本文針對(duì)多集群風(fēng)機(jī)提出一種基于DO的控制參數(shù)優(yōu)化策略,其貢獻(xiàn)可概括為以下三點(diǎn):

1)分別基于兩個(gè)WF(各包括5臺(tái)WT)提出梯次啟動(dòng)自適應(yīng)慣性下垂控制策略,以實(shí)現(xiàn)電網(wǎng)系統(tǒng)頻率支撐。其中,WF1中的WT按角速度被分為集群1和集群2。前者在負(fù)荷發(fā)生變化時(shí)立即參與頻率調(diào)節(jié),后者在前者的轉(zhuǎn)子角速度恢復(fù)時(shí)運(yùn)行,實(shí)現(xiàn)風(fēng)機(jī)的梯次啟動(dòng),進(jìn)而顯著減少一次、二次甚至三次頻率跌落。

2)為了降低現(xiàn)場(chǎng)調(diào)參復(fù)雜度與試錯(cuò)法的不確定性,提高控制器的自適應(yīng)能力,設(shè)計(jì)了基于DO的梯次啟動(dòng)自適應(yīng)慣性下垂控制器參數(shù)設(shè)計(jì)框架,用于調(diào)整控制器的8個(gè)未知參數(shù)。

3)仿真結(jié)果表明,本文所提控制器參數(shù)優(yōu)化框架與試錯(cuò)法相比,在各種負(fù)荷增加場(chǎng)景下均能獲得良好的頻率支撐效果。尤其是當(dāng)負(fù)荷增加50 MW時(shí),基于DO的SFD和TFD分別為0.0365 Hz和0.034 5 Hz,相比試錯(cuò)法(SFD和TDF分別為0.0411 0 Hz和0.040 0 Hz),穩(wěn)定性提高了11.34%和13.74%。

本文僅考慮風(fēng)電機(jī)組參與系統(tǒng)慣性和一次調(diào)頻過(guò)程,時(shí)間尺度為10 s左右,因此在這一暫態(tài)過(guò)程中,可認(rèn)為風(fēng)速不變,風(fēng)機(jī)出力大小不變;并且考慮到轉(zhuǎn)速限制,認(rèn)為載荷不會(huì)影響風(fēng)機(jī)的調(diào)頻能力。若要考慮更長(zhǎng)時(shí)間尺度的調(diào)頻控制策略,則風(fēng)速隨時(shí)間變化的特性不可忽略,這也是本文后續(xù)研究?jī)?nèi)容之一。