Ground-state phase diagram,symmetries,excitation spectra and finite-frequency scaling of the two-mode quantum Rabi model

Yue Chen(陳越), Maoxin Liu(劉卯鑫), and Xiaosong Chen(陳曉松),?

1CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3School of Systems Science,Beijing Normal University,Beijing 100875,China

Keywords: two-mode quantum Rabi model, superradiant phase transition, Nambu-Goldstone mode, finitefrequency scaling,Schrieffer-Wolff(SW)transformation

1.Introduction

The quantum phase transition (QPT) is an important issue in the area of quantum optics and condensed-matter physics.[1-14]Traditional studies of the quantum phase transition mostly focus on the thermodynamic limit,which requires the number of microparticles to approach infinity.However,recent theoretical studies show that a second-order quantum phase transition can occur when the ratio of atom transition frequency to cavity frequency approaches infinity whereas the system contains only one atom, such as the quantum Rabi model(QRM).[15,16]

The QRM describes the interaction between a photon field and a two-level system,[17,18]which is one of the simplest models for studying the light-matter interaction and plays a significant role in quantum optics,[19]quantum information[20]and condensed-matter physics.[21]The single-mode QRM can be realized experimentally by a photonic analog simulator,based on light transport in femtosecond-laser-written waveguide superlattices, which provides an experimentally accessible test bed to explore the physics of light-matter interaction in the deep strong coupling regime.[22]Recently, a trappedion experiment using a171Yb+ion in a Paul trap observed this quantum phase transition,which opens up a new window for controllable study of the quantum phase transition without requiring the thermodynamic limit.[23]Moreover,Chenet al.experimentally simulated the occurrence of an equilibrium superradiant phase transition beyond the no-go theorem by introducing the antisqueezing effect based on the platform of nuclear magnetic resonance.[24]With the rapid experimental progress in accessing the strong,[25,26]the ultrastrong,[27-29]and the deep strong[30,31]coupling regimes,the QRM has received much attention.[32-54]Since the quantum phase transition and critical phenomena in the QRM are found, further study on the scaling behaviors of the Rabi and the Dicke models has revealed that these two models belong to the same universality class.[55]These progresses bring a new insight into the quantum phase transitions without the thermodynamic limit.However,how the number of cavity fields of QRM influences the quantum phase transition remains an open question.Moreover, the interaction between a two-mode cavity field and a three-level system leads to many important phenomena,such as electromagnetically induced transparency[56]and dark state,[57]which are profitable in the precise control of coherent population trapping and transfer.[58]The three-level system is also important in quantum information, referred to as qutrit.Compared with the two-level scheme,the quantum key distribution based on qutrits is more resistant to attack,[59,60]and the quantum computation using qutrits shows a faster speed and a lower error rate.[61,62]Haynet al.studied quantum phase transitions by a generalized Holstein-Primakoff transformation and revealed that it exhibits two superradiant quantum phase transitions, which can be both of first and second orders.[63]Corderoet al.found that the polychromatic ground-state phase diagram can be divided into monochromatic regions by a variational analysis.[64]Zhanget al.reported an analytical calculation of the ground-state phase diagram,scaling function,and critical exponents for the two-mode three-level QRM.[8]However,the quantum phase transition in a two-mode photon field model with few degrees of freedom,i.e.,the two-mode QRM,has not been extensively studied.In this work, we consider a two-level atom interacting with two different photonic field modes.Since the model symmetry shifts as the parameter of the model Hamiltonian changes, we expect there would arise rich critical phenomena.To identify the possible quantum phases and quantum phase transitions involved in a two-mode model is helpful in further understanding the light-matter interaction models and extending their applications.

The paper is organized as follows.In Section 2,the lowenergy effective Hamiltonians for four different phases are derived when the ratio of the atom frequency to the photon frequency approaches infinity and the ground-state phase diagram is obtained.In Section 3, the symmetries of two-mode QRM are studied.In Section 4,the excitation spectra,critical photon number and fluctuations of field quadratures are analytically calculated.In Section 5, the finite-frequency exponents are analytically derived and the finite-frequency scaling relations of average photon numbers are verified numerically.Finally,a brief summary and conclusions are presented in Section 6.

2.The effective Hamiltonian and ground-state phase diagram

The two-mode quantum Rabi model(QRM)describes the interaction between two cavity fields and one two-level atom.Its Hamiltonian is

whereσzis the Pauli matrix for a two-level atom,σ+andσare the raising and lowering operators of spin respectively,anda(a?) andb(b?) are the annihilation (creation) operators for two cavity fields respectively.The parametersω,Ω,λ1, andλ2are the cavity field frequency, transition frequency of the atom and the coupling strength parameters respectively.The coupling of the first cavity fieldawith spin represents the interaction of the electric field with atom,while that of the second cavity fieldbwith spin represents the interaction of magnetic field with atom.Such a coupling mechanism has been investigated in the single-mode QRM and can be implemented in circuit quantum electrodynamics systems, where artificial Josephson atoms are coupled both capacitively and inductively to a superconducting resonator.[65]It has also been studied in the two-mode Dicke model[66]and experimentally realized with continuous translational symmetry breaking along one direction in a quantum gas.[67]

Here|↓〉 and|↑〉 are the low-energy and high-energy eigenstates ofσzrespectively.|m1〉 and|m2〉 (m1,m2∈N)are the eigenstates ofa?aandb?brespectively.The parity operatormeasures the odd-even parity of total excitation number and commutes withH.Though there is an exact solution for the one-mode QRM,[39]a lack of a closed-form solution makes it not directly applicable to investigate the QPT,thus the approximately analytical and the numerical methods are applied to study the QPT.The same situation exists for the two-mode QRM.When the system approaches the classical regime,the mean-field approximation is effective,but when the system is completely quantum,it fails.To settle this problem,we apply Schrieffer-Wolff(SW)transformation to derive the low-energy effective Hamiltonian of the two-mode QRM.

Based on the SW transformation,in the limitη=Ω/ω →∞,we find a unitary transformation

which makes the transformed HamiltonianUHU?free of coupling terms between spin subspacesH↓andH↑.Neglecting the high-order terms and under the conditionη ?1,the effective Hamiltonian is

Considering the limitη=Ω/ω →∞, and projecting the Hamiltonian to the spin-down subspace,we can obtain the effective Hamiltonian of the normal phase(NP)as

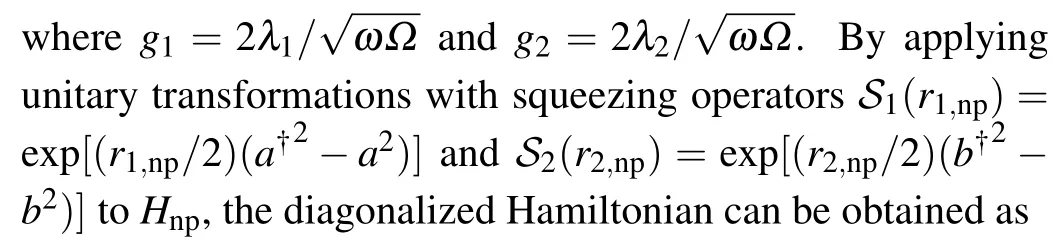
where

which are the excitation energy of two cavity fields, respectively,and

is the ground state energy.The energy eigenvalues and eigenstates in the NP are respectively

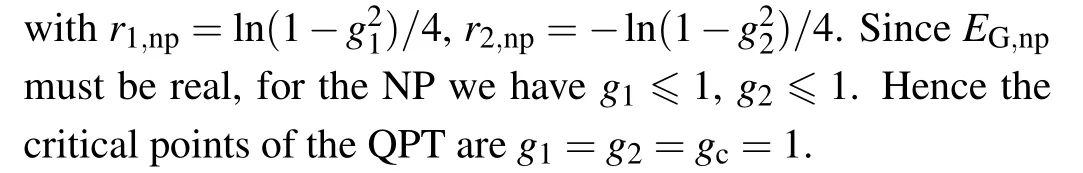
Forg1＞1 org2＞1,the Eq.(4)fails,indicating the number of photons occupied in the cavity fields becomes proportional toηso that the higher-order terms cannot be neglected,i.e., the ground state comes into the superradiant phase.It also suggests the low-energy subspace changes.In order to obtain the new low-energy effective Hamiltonian, we transform the original two-mode quantum Rabi Hamiltonian by displaying two field modesaandbwith displacement operatorsD1(α)= eα(a?-a)andD2(β)= eiβ(b?+b),whereαandβare real,

The eigenstates of atomic part of Hamiltonian,i.e.,(Ω/2)σz-2λ1ασx-2λ2βσy,are

where the new transition frequency

In the new representation, after expressingσx,σy, andσzin the terms of ?σx, ?σy,and ?σzand substituting them into Eq.(10),the displaced Hamiltonian can be expressed as

The requirement that the block-diagonal perturbation terms vanish in the last line gives

There are three sets of solutions of the above equations, and the ground-state energy of Hamiltonians corresponding to the above solutions is discussed as follows.

(i)The first modeais displaced with the second modebunchanged.We have

Substituting Eq.(14)into Eq.(12),and applying SW transformation again, we can obtain the low-energy effective Hamiltonian as

where the excitation energy of two cavity fields are respectively

The energy eigenvalues and eigenstates in the ESP are respectively

where

The eigenstates are degenerate and have a spontaneous broken parity symmetry as we can see from nonzero coherence of the field〈a〉=±αgand〈b〉=±βg.To ensure the ground state energy is real,g1andg2have to satisfyg1≥1,g1≥g2.

(ii)The second modebis displaced with the first modeaunchanged.We have

Similar as before, we can obtain the low-energy effective Hamiltonian as

where the excitation energy of two cavity fields are respectively

The energy eigenvalues and eigenstates in the MSP are respectively

where

To ensure the ground state energy is real,g1andg2have to satisfyg2≥1,g2≥g1.

(iii)Both the modeaandbare displaced,we have

In this set of solution, the values ofαandβare not unique.We supposeβ=μα,μ ∈(-∞,∞) andμ/=0, thus from the above equations we obtain

Substituting Eqs.(31)and(32)into Eq.(12),by the approach of SW transformation, the low-energy effective Hamiltonian of electromagnetic superradiant phase(EMSP)is

where

where the single-photon energy of two cavity fields are respectively

The energy eigenvalues and eigenstates in the EMSP are respectively

where

To ensure the ground state energy is real,g1andg2have to satisfyg1=g2=g≥1.

In the above three cases, if not equal to zero, there are two values forα=±αgorβ=±βg, leading to an identical spectrum,which is correlated with the parity symmetry of the system.The high-order corrections in Eqs.(4),(15),(23),and(33) vanish in theη →∞limit, therefore theHnp,Hesp,HmspandHemspare exact low-energy effective Hamiltonian for the NP, ESP, MSP and EMSP respectively.The Eqs.(7), (17),(25),and(35)give the ground state energy of four phases respectively.Take the limitη →∞, the rescaled ground state energy of four phases are respectively

The above exact solutions show thatg1=1,g2=1 is the quadruple point.The phase diagram is displayed in the Fig.1.

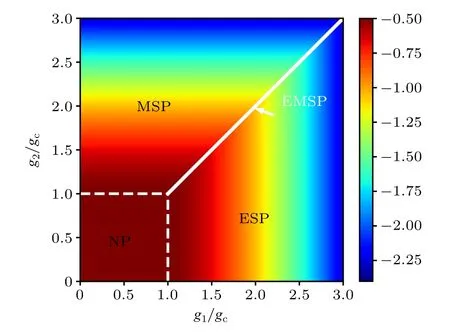
Fig.1.The ground-state phase diagram as a function of g1/gc and g2/gc.The regime g1/gc ＜1 and g2/gc ＜1 denotes the normal phase(NP).The regime g1/gc ≥1 and g1/gc ＞g2/gc denotes the electric superradiant phase(ESP).The regime g1/gc ≥1 and g2/gc ＞g1/gc denotes the magnetic superradiant phase(MSP).The white solid line denotes the electromagnetic superradiant phase(EMSP)with regime g1/gc=g2/gc ≥1.

For the phase transition from the NP to the ESP,

Therefore,this phase transition is of second order.Similarly,it is not hard to confirm that the phase transition from the NP to the MSP is also of second order.When considering the phase transition from the ESP to the MSP,we take the derivatives ofeG,espandeG,mspalong the unit vectorwherexandyare unit vectors along the horizontal and vertical axes respectively.There are

Therefore the phase transition from the ESP to the MSP is of first order.In Fig.2, we plot the rescaled ground-state energy, its first-order and second-order derivatives from the NP to the ESP.It is obvious thateGand deG/dg1are continuous atg1=1.0, while d2eG/dg21is not.Since the symmetry of the phase diagram, for the phase transition from NP to MSP,the ground-state energy,its first-order and second-order derivatives are similar with that of the phase transition from NP to ESP.See Appendix A for a detailed derivation of the effective Hamiltonians and their analytical diagonalization.

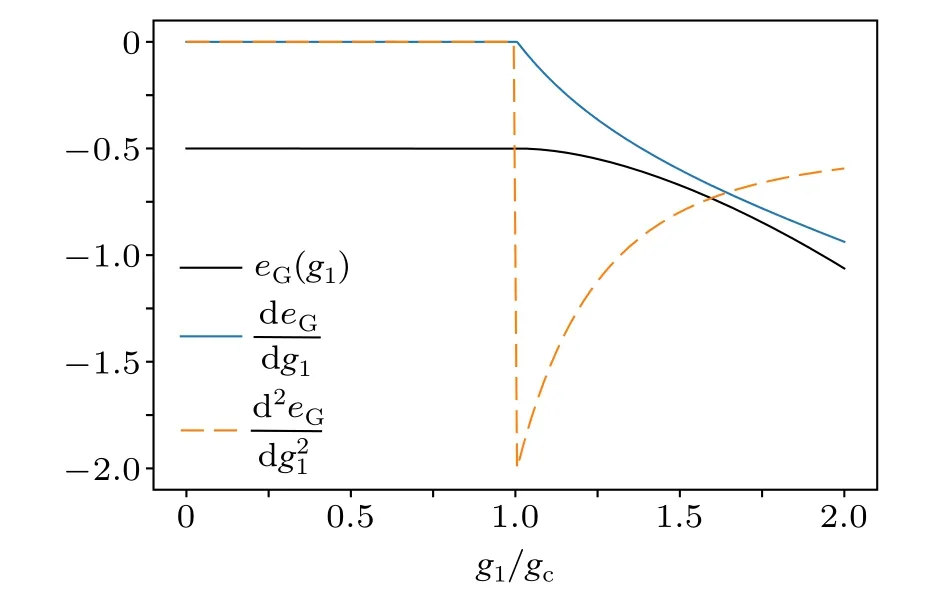
Fig.2.The ground-state energy eG, its first-order derivative deG/dg1 and second-order derivative d2eG/dg21 from the NP to the ESP.For simplicity,we take ω=1.0.We can see that eG and deG/dg1 are continuous at g1=1.0,while d2eG/dg21 is not.Thus the phase transition from NP to ESP is of second-order.

3.Symmetries

To understand the phase transition,it is necessary to discuss the breaking of symmetries.Firstly,the Hamiltonian(1)has a discreteZ2symmetry.Take a transformation:x →-x,y →-y,we have

It is known from Eqs.(20),(21),(28),and(29)that the ground states of ESP and MSP are doubly degenerate.Therefore,the phase transition from the NP to the ESP (MSP) is associated with the breaking of the discreteZ2symmetry.

Whenλ1=λ2=λ,the Hamiltonian becomes

For the above Hamiltonian,we find a conserved quantity

Ifλ1/=λ2,there is nothing we can know from the above equation.However,in the case ofλ1=λ2=λ(g1=g2),we find that

Therefore,the HamiltonianHλis invariant under the continuousU(1)transformation.

Moreover, wheng ＞gc=1, the system enters into the EMSP in which the ground state is infinitely degenerate since for a given ground-state energy, an infinite number of values of the parameterμin the eigenstate can be taken, as long as the conditionα2+β2=(η/4)(g2-g-2)is satisfied.This signifies that the continuousU(1)symmetry breaks down in the EMSP.

4.The excitation spectra, photon number and fluctuations of field quadratures

4.1.Excitation spectra

Since we don’t know whether|1,0〉or|0,1〉is the first excited state,the excitation energy is the smaller one of two values of energy from|0,0〉to|1,0〉and|0,1〉.In the NP,when the system excites from the ground state to|1,0〉, the energy needed is the single-photon energy of cavity fielda, which is given by the first expression in Eq.(6).When the system excites from the ground state to|0,1〉, the energy needed is the single-photon energy of cavity modesb,which is given by the second expression Eq.(6).The excitation energy of the whole system is

In the ESP,when the system excites from the ground state to|1,0〉and|0,1〉,two values of energy needed are respectively given by the two expressions in Eq.(18).The excitation energy of the whole system is

In the MSP,when the system excites from the ground state to|1,0〉and|0,1〉,two values of energy needed are respectively given by the two expressions in Eq.(26).The excitation energy of the whole system is

In the EMSP, when the system excites from the ground state to|1,0〉 and|0,1〉, two values of energy needed are respectively given by the two expressions in Eq.(36).The excitation energy of the whole system is

Therefore, we know that from the NP to the ESP,ε～|g1-gc|1/2, which gives its critical exponent as 1/2.From the NP to the MSP,ε～|g2-gc|1/2, thus the critical exponent of excitation energy is also 1/2.In Fig.3, the excitation energy is shown when the system excites from the groundstate to the lowest excited state.For simplicity, we takeω= 1.0.It has been shown that the breaking of continuous symmetry leads to a gapless excitation spectrum(Nambu-Goldstone mode).[68-70]There are three critical lines in this figure:g1= 1,0 ≤g2≤1;g2= 1,0 ≤g1≤1 andg1=g2≥gc=1.The excitation energy in these three lines becomes zero.For the diagonal critical line, the continuousU(1) symmetry breaks down, and the corresponding mode is the Nambu-Goldstone mode.For the system with singlemode photon, the emergence of Nambu-Goldstone needs the rotating-wave approximation and strong collective atomphoton coupling.[65,71-73]However,the rotating-wave approximation breaks down when the collective atom-photon coupling is strong.Here no rotating-wave approximation is applied and we show that Nambu-Goldstone mode can exist when the system has a strong atom-photon coupling.This phenomenon also emerges in the two-mode Dicke model.[66]

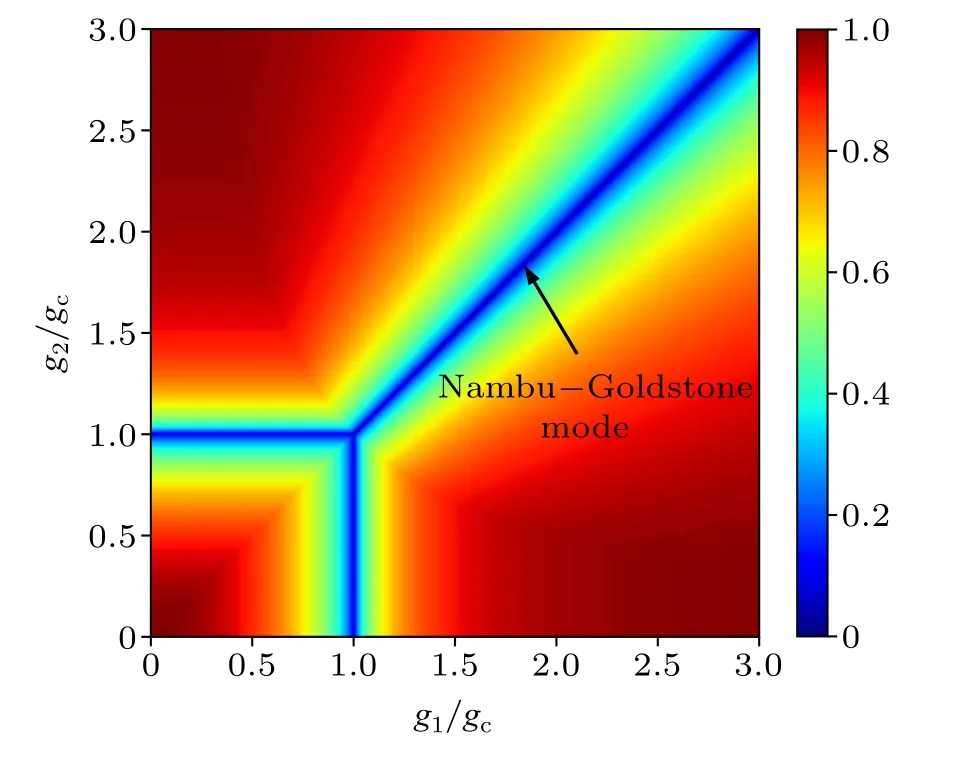
Fig.3.The excitation spectra as a function of g1 and g2 with ω =1.0.There are three critical lines in this figure:g1=1,0 ≤g2 ≤1;g2=1,0 ≤g1 ≤1 and g1 =g2 ≥gc =1.The excitation energy in these three lines becomes zero.For the diagonal critical line, the continuous U(1) symmetry breaks down,and the corresponding mode is the Nambu-Goldstone mode.

4.2.Critical photon number

For the NP, the rescaled average photon number of the first cavity fieldain the ground state is

Similarly, the rescaled average photon number of the second cavity fieldbin the ground state is

Whenη →∞,n1,np=0,andn2,np=0.Therefore,there is no collective excitation for both cavity fieldsaandbwhen the system is in the NP.

For the ESP, the rescaled average photon number of the first cavity fieldain the ground state is

Similarly, the rescaled average photon number of the second cavity fieldbin the ground state is

Whenη →∞,n1,esp=(1/4)(g21-g-21)andn2,esp=0.Therefore,there is collective excitation for cavity fieldabut no collective excitation emerges for cavity fieldb.The coupling of cavity fieldawith atom represents the interaction of electric field and spin, that is why this phase is called the electric superradiant phase.From the NP to the ESP,the rescaled average photon numbern1is an order parameter with critical exponent as 1.

For the MSP,the rescaled average photon number of the first cavity fieldain the ground state is

The rescaled average photon number of the second cavity fieldbin the ground state is

Whenη →∞,n1,msp=0 andn2,msp=(1/4)(g22-g-22).Therefore,there is no collective excitation for cavity fieldabut collective excitation emerges for cavity fieldb.The coupling of cavity fieldbwith atom represents the interaction of magnetic field and spin, that is why this phase is called the magnetic superradiant phase.From the NP to the MSP,the rescaled average photon numbern2is an order parameter with critical exponent as 1.

For the EMSP,the rescaled average photon number of the first cavity fieldain the ground state is

The rescaled average photon number of the second cavity fieldbin the ground state is

Whenη →∞,n1,emsp=(1/(4(1+μ2)))(g2-g-2),n2,emsp=(μ2/(4(1+μ2)))(g2-g-2).Therefore,collective excitations emerge for both cavity fieldsaandband this phase is called the electromagnetic superradiant phase.

4.3.The fluctuations of field quadratures

In the ground state of NP,for the first cavity field,it is not hard to obtain that the fluctuation of position operator of the first oscillatoris

Similarly,for the momentum operatorwe have

For the second cavity field,

While the Δxplays an analogous role of the diverging length scale in the extended quantum system, the critical point accompanies an infinite amount of squeezing in the momentum quadraturep, so that it remains in the minimum uncertainty state for anyg1andg2, i.e., Δx1,npΔp1,np= 1/2,Δx2,npΔp2,np=1/2.

In the ESP,it is not hard to obtain that the fluctuation of quadratures of the cavity fieldais respectively

For the cavity fieldb,it is easy to obtain

In the MSP, the fluctuations of quadratures of the cavity fieldaare respectively

For the second cavity field,it is easy to obtain

In the EMSP,the fluctuations of quadratures of the cavity fieldaare respectively

For the cavity fieldb,it is easy to obtain

In the ESP, MSP and EMSP, the system also remains in the minimum uncertainty state for anyg1andg2, i.e., Δx1Δp1=1/2,Δx2Δp2=1/2.In the four phases,the critical exponents of Δx1and Δp1are-1/4 and 1/4 respectively,which are the same with that in the single-mode QRM.However, the critical exponents of Δx2and Δp2are 1/4 and-1/4 respectively,which are the opposite with that in the single-mode QRM.[15]This may be attributed to the fact that the coupling of fieldawith atom in our model represents the interaction of electric field with spin, which is the same as that in the single-mode QRM.However the coupling of fieldbwith atom represents interaction of the magnetic field with spin, which is different from that in the single-mode QRM.

5.Finite-frequency scaling

To derive analytically the finite-frequency scaling exponents of important quantities,we need to take the higher-order(up to fourth order) correction of perturbation into consideration.After adding the higher-order correction, the Hamiltonian of the NP is

where the fourth-order correction adds a quartic potential for the cavity field.The above Hamiltonian cannot be analytically diagonalized,but we can use a variational method to derive its expectation value.We propose a trial wave function of ground state as

wheres1ands2are variational parameters.The energy expectation value in the ground state is

To decide the minimum ofE00(s1,s2),it is required that

At the critical pointg1=g2=gc=1, the above equations become

By canceling the es2term in these equations and definingu=ηe6s1,we have

The three solutions for Eq.(80) areTo ensure the squeezing operatorS1(s1)is unitary,the parameters1has to be real.Hence we have only one sensible solutionu=2 and

To know whether the extreme values we obtained are minimum, we calculate the second-order partial derivatives ofE00(s1,s2)as

It is evident that?2E00/?s21＞0 and?2E00/?s22＞0.Therefore,we have the minimum point as the critical parameters

Substituting the above values ofs1ands2into Eq.(77), we can obtain the minimum expectation value of energy corresponding to the trial wave function as the approximation of ground-state energy

When the higher-order correction is not taken into consideration, the ground-state energy in the NP at the critical point isEG,np(g1=g2=gc)=-(Ω/2)-ω.Thus we can obtain the finite-frequency correction for the rescaled ground-state energy at critical point is

The rescaled cavity photon number of cavity fieldais

The rescaled cavity photon number of cavity fieldbis

The finite-frequency scaling exponents ofeG,n1candn2care found to be same as those of corresponding observables for the one-mode QRM,[15]Dicke model[74]and LMG model.[75,76]The leading-order corrections of the fluctuations of cavity field quadratures of modeaare respectively

The leading-order corrections of the fluctuations of cavity field quadratures of modebare respectively

We assume that the excited states corresponding to the quantum numberm1,m2are

At the critical point, substituting the relevant parameters and simplifying the result,we can obtain

For the cavity fielda, the energy correction from the ground state(n1=0,n2=0)to the first excitation state(m1=1,m2=0)is

For the cavity fieldb, the energy correction from the ground state(n1=0,n2=0)to the first excitation state(m1=0,m2=1)is

which is the same with that of cavity fielda.Therefore,for the whole system,the correction of excitation energy is

Now we confirm the validity of the low-energy effective Hamiltonians in Eqs.(4), (15), (23), and (33).For the phase transition from the NP to the ESP, according to the scaling theory of phase transition, the critical behavior of the average photon number of cavity fieldaat critical point isn1～|g1-gc|γ～η-γ/ν,(g1→gc),whereγandνare the critical exponents ofn1andηrespectively.The finite-frequency scaling ansatz predicts that,for a largeηand near the critical point,the expectation value ofn1can be written in terms of a variable-dependent scaling functionf1(x)

From Subsection 4.2 and Eq.(87), we know thatγ=1, and the finite-frequency scaling exponent ofn1is-γ/ν=-2/3.Therefore,we haveν=3/2.Equation(96)becomes

If all the data aboutn1calculated from numerically diagonalizing the two-mode quantum Rabi Hamiltonian Eq.(1)for many variousg1andηis plotted in a rescaled axis,there must be a single curve that reveals the scaling functionf1(x).In Fig.4,one can indeed see that all curves collapse into a single curve,revealing an observable-dependent scaling functionf1(x).

For the phase transition from the NP to the MSP,there is a similar scaling relation for the averaged photon numbern2

wheref2(x)is another scaling function.The expectation valuesn2for variousg2andηare plotted in Fig.5, from which one can see that all curves collapse into a single curve.Based on the numerical confirmation,we conclude that the effective Hamiltonians in Eqs.(4), (15), (23), and(33)are indeed correct low-energy effective Hamiltonians of the two-mode QRM in the limitη →∞.

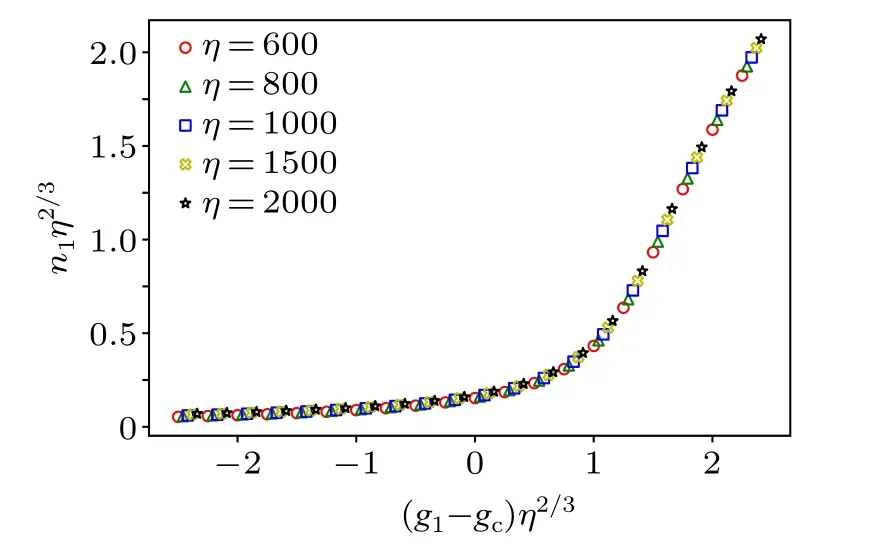
Fig.4.For the phase transition from NP to ESP, the values of averaged photon number n1 calculated by numerically diagonalizing the two-mode quantum Rabi Hamiltonian for many various g1 and η are plotted in a rescaled axis.One can clearly see that all curves collapse into a single curve,revealing an observable-dependent scaling function f1(x).

6.Summary and conclusions

We investigate the ground-state phase diagram, symmetries, excitation spectra and finite-frequency scaling of the two-mode quantum Rabi model.Based on the Schrieffer-Wolff transformation, we obtain the low-energy effective Hamiltonians for various phases of two-mode quantum Rabi model, by which we find the quartic critical point and a rich phase diagram, including a normal phase, an electric superradiant phase, a magnetic superradiant phase and an electromagnetic superradiant phase.The phase transitions from the normal phase to the electric(magnetic)superradiant phase are of second order with the averaged photon number as order parameter,and associate with the breaking of a discreteZ2symmetry,while the phase transition from the electric superradiant phase to the magnetic superradiant phase is of first order.If the collective atom-photon coupling strength parameters are equal, there is a continuousU(1) symmetry, which breaks down in the electromagnetic superradiant phase because the ground state of this phase is infinitely degenerate.We calculate analytically the excitation energy, photon number and fluctuations of field quadratures.In the excitation spectra,there are three critical lines in which the excitation energy becomes zero and the Nambu-Goldstone mode is found.The critical exponents of excitation energy and photon number are the same with those of the single-mode quantum Rabi model.The critical exponents of Δxand Δpof the first cavity fieldain the four phases are the same with those in the single-mode quantum Rabi model,while the critical exponents of the Δxand Δpof the second cavity fieldbare the opposite with that in the single-mode quantum Rabi model.At last, in order to confirm the validity of the low-energy effective Hamiltonians of four phases analytically derived by us, we obtain the analytical finite-frequency scaling exponents and verify the finitefrequency scaling relation of averaged photon number of two cavity fields by numerically diagonalizing the two-mode quantum Rabi Hamiltonian.The results show that all data for many differentg1(g2)andηcollapses into a single curve,concluding that the Hamiltonians we calculated are correct in the limitη →∞.

Appendix A:Derivation of effective Hamiltonian

In this section, we give detailed derivation of lowenergy effective Hamiltonians and ground-state energy by the Schrieffer-Wolff (SW) transformation.Based on the idea of perturbation theory,Hcan be written in the form of

where

According to Schrieffer-Wolff (SW) transformation, we need to find a unitary operatorU= eSsuch that the transformation ?H=UHU?convertsHinto a block-diagonal form.Define a superoperatorLas

We expandSandLin series

whereLnA=[Sn,A].If we splitVinto block-diagonal partVdand block-off-diagonalVod,the leading-order terms ofSare

whereL0A=[H0,A]and

for an arbitrary operatorA.The leading-order terms of lowenergy effective Hamiltonian(up to fourth order)are given by

whereP=|↓〉〈↓| is the project operator onto the low-energy space.

For the Hamiltonian of two-mode QRM,it is not hard to confirm that the perturbation Eq.(A3) is block-off-diagonal,namely,Vd=0 andVod=V.Therefore, we haveS2=0 and ?H(1)= ?H(3)=0.

Now we calculateS1.According to Eqs.(A7)and(A10),

We need to first calculate the temporal evolution ofVod,

For a one-dimensional harmonic oscillator with Hamiltonianωa?a, the temporal evolution of positionxand momentumpcan be derived by the Heisenberg equation as

wherex=x(0)andp=p(0).

Substituting Eq.(A17)into Eq.(A16)and using operator relation eiσzθ=cosθ+iσzsinθ, then substituting the result into Eq.(A15),we obtain

In order to evaluateS3, we need to calculate=[S1,[S1,[S1,H0]]].From Eq.(A7)we know that

After neglecting the high-order small quantities,we can obtain

SinceVd=0, the second term in the right side of Eq.(A9)vanishes.Similar to the procedure of calculatingS1, we can obtain

According to Eqs.(A12)and(A14), ?H(2)and ?H(4)can be calculated as

Summing up the above results, the low-energy effective Hamiltonian is

Under the conditionΩ ?ω, ?H(2)and ?H(4)can be simplified,thus we have

Considering the limitη=Ω/ω →∞, and projecting the Hamiltonian to the spin-down subspace,we can obtain the effective Hamiltonian of the normal phase(NP)as

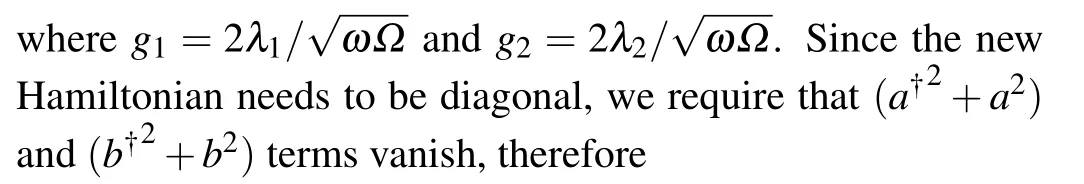
Their solutions are

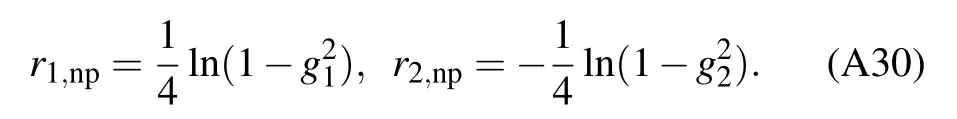
Substituting these solutions to Eq.(A28), the diagonalized Hamiltonian can be obtained as

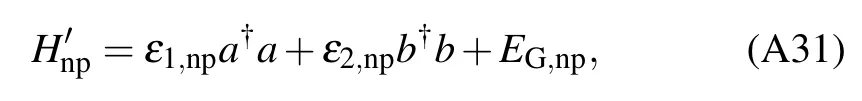
where

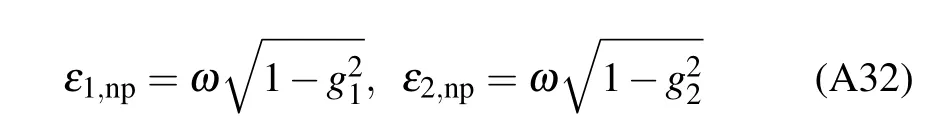
are the excitation energy of two cavity fields respectively and

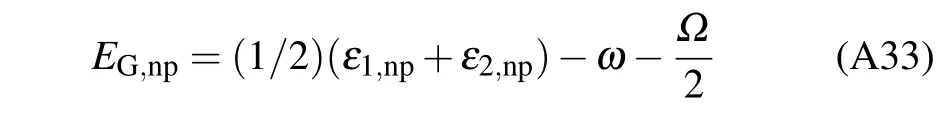
is the ground-state energy.The energy eigenvalues and eigenstates in the NP are respectively

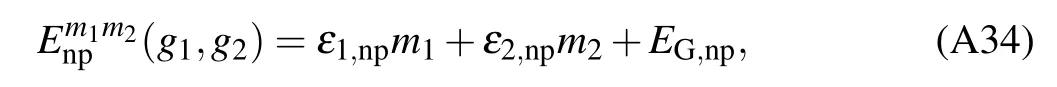
SinceEG,npmust be real,for the NP we haveg1≤1,g2≤1.

Forg1＞1 org2＞1,the discussion and calculations are given in the main text.

Acknowledgments

We thank Gaoke Hu for his helpful discussion on the finite-frequency scaling.This work was supported by the National Natural Science Foundation of China (Grant No.12135003).The authors acknowledge HPC Cluster of ITP-CAS for supplying computation resources.