改進的多端柔性直流系統多點直流電壓無差協調控制策略

李從善, 張曉偉, 和萍, 武小鵬, 趙琛

(鄭州輕工業大學電氣信息工程學院, 鄭州 450053)

隨著能源結構的不斷調整,大容量電力電子器件在電網中的滲透率逐步提高,在源、網、荷、儲4個領域都呈現出電力電子化趨勢。在輸電系統方面,基于電壓源換流器的多端柔性直流輸電系統(voltage source converter based multi-terminal high voltage direct current, VSC-MTDC)是未來遠距離輸電技術的重要發展方向之一,逐漸成為新能源并網的最佳選擇[1-3]。

目前,應用于VSC-MTDC系統的站間控制策略大致分為3種:主從控制、裕度控制和直流電壓下垂控制[4-6]。其中下垂控制利用多個換流站的功率調節能力,實現不平衡功率的快速分配,直流電壓響應特性較好,但是存在直流電壓偏差較大的問題。

針對換流站采用下垂控制消納不平衡功率時固有的直流電壓偏差問題,國內外學者進行了大量研究,目前主要分為以下3種控制方法。

第一種方法是通過改進下垂系數,實現不平衡功率的合理分配,減小直流電壓的偏差。文獻[7-10]通過自適應調整下垂系數,有效減小了直流電壓的偏差。然而,換流站實際有功功率傳輸值與參考值之間的偏差持續存在,直流電壓偏差也一直存在,不利于系統的穩定運行。

第二種方法是通過改變換流站的運行方式來實現直流電壓的無差調節。文獻[11]提出將直流電壓誤差通過比例-積分(proportion-integration,PI)控制器疊加到有功功率環上,利用PI控制器的無靜差特性,實現直流電壓的無差調節。文獻[12]提出一種結合主從控制和下垂控制的聯合控制策略,通過切換控制方式,實現直流電壓的無差調節。文獻[13]提出一種多點電壓協調控制策略,最小化換流站動態功率偏差的同時,提升了直流電壓的性能。然而,上述控制策略的本質是將下垂站轉變為定直流電壓控制站,喪失了下垂控制多站協同消納不平衡功率的優勢。

第三種方法是通過調整有功功率參考值,達到直流電壓無差調節的目的。文獻[14]通過采集直流系統的不平衡功率,疊加到有功功率參考值上,實現下垂曲線的平移。文獻[15]證明了在直流系統受到功率擾動后,各換流站保持輸出功率不變的同時,無法將直流電壓恢復至額定值。進而提出一種兼具換流站功率變化最小以及直流電壓偏差最小的協調控制策略,實現直流電壓的“偽”無差調節。

針對換流站采用傳統下垂控制消納不平衡功率時固有的直流電壓偏差問題,現基于第三種方法,提出一種優化協調控制策略,將直流網絡不平衡功率作為前饋補償量注入傳統下垂控制中,通過平移下垂曲線來實現直流電壓的準無差調節。同時將偏差下垂控制引入定有功功率換流站,避免不平衡功率過大導致下垂站滿載而失去控制直流電壓的能力。最后,通過PSCAD/EMTDC建立五端VSC-MTDC仿真模型,仿真結果驗證所提控制策略的有效性。

1 傳統下垂控制電壓偏差分析

1.1 VSC-MTDC系統模型

五端VSC-MTDC系統結構如圖1所示。VSC1～VSC5代表5個電壓源型換流站,直流側通過直流網絡并聯,交流側與各自的交流電網連接。

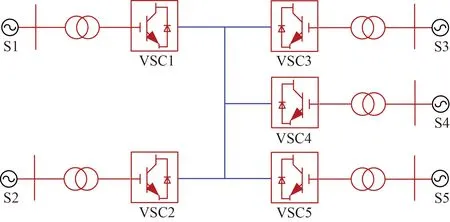
圖1 VSC-MTDC系統結構圖Fig.1 VSC-MTDC system structure diagram

單個VSC結構的拓撲結構如圖2所示。

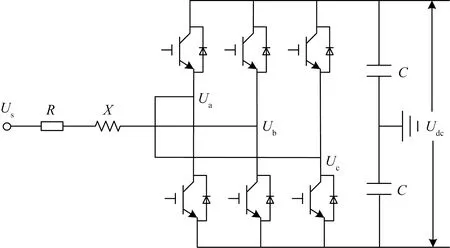
在三相坐標系下,Us為交流電網電壓;Ua、Ub、Uc分別為交流電網電壓;R、X分別為VSC交流側等效電阻和電抗;C為直流側電容;Udc為直流側電壓

在兩相旋轉dq坐標系下,VSC的數學模型為

(1)

式(1)中:L為交流側等效電感;Usd、Usq分別為電網電壓的d、q軸分量;Ud、Uq分別為 VSC交流側電壓的d、q軸分量;isd、isq分別電網電流的d、q軸分量;ω為電網電壓矢量同步旋轉角速度。

1.2 傳統下垂控制電壓偏差分析

類比傳統發電機一次調頻特性,下垂控制無需站間通信,利用直流電壓與有功功率特性曲線,實現不平衡功率的快速分配和直流電壓的穩定控制。直流電壓-有功功率(Udc-Ps)控制器結構和特性曲線如圖3和圖4所示。

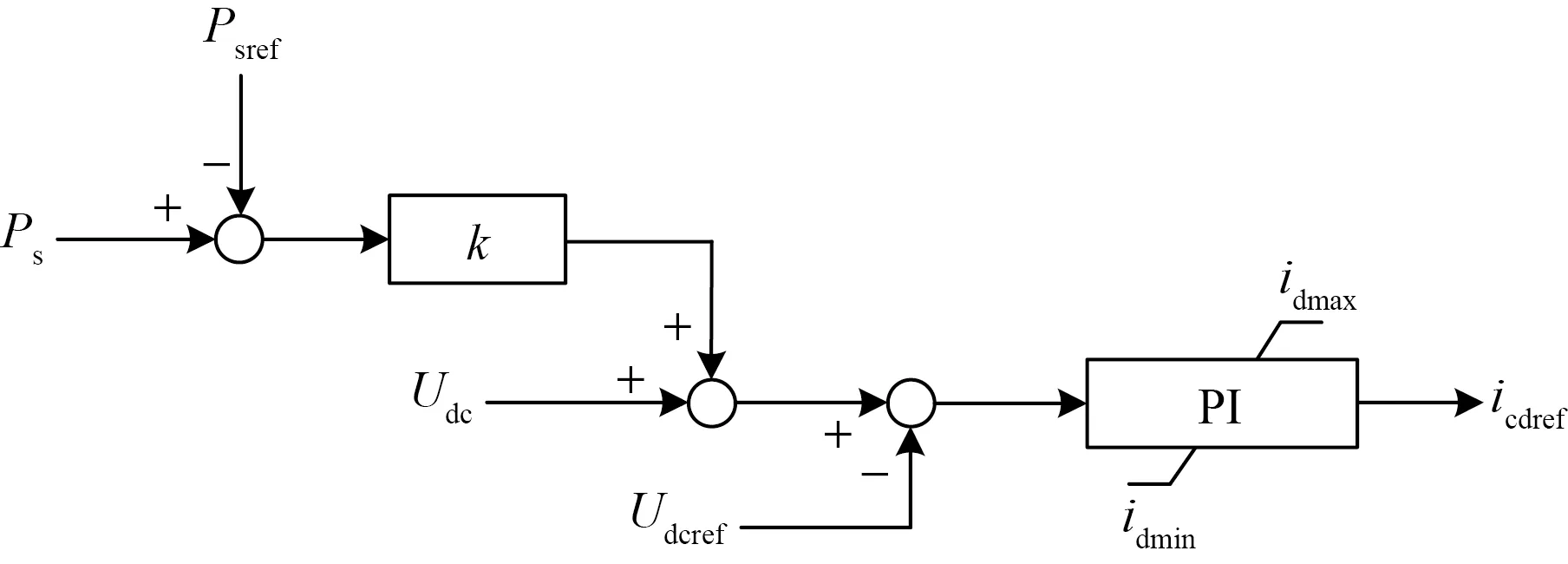
Udc和Udcref分別為直流側電壓實測值和參考值;Ps、Psref和Psmax分別為換流站有功功率實測值、參考值和額定容量;k為下垂系數

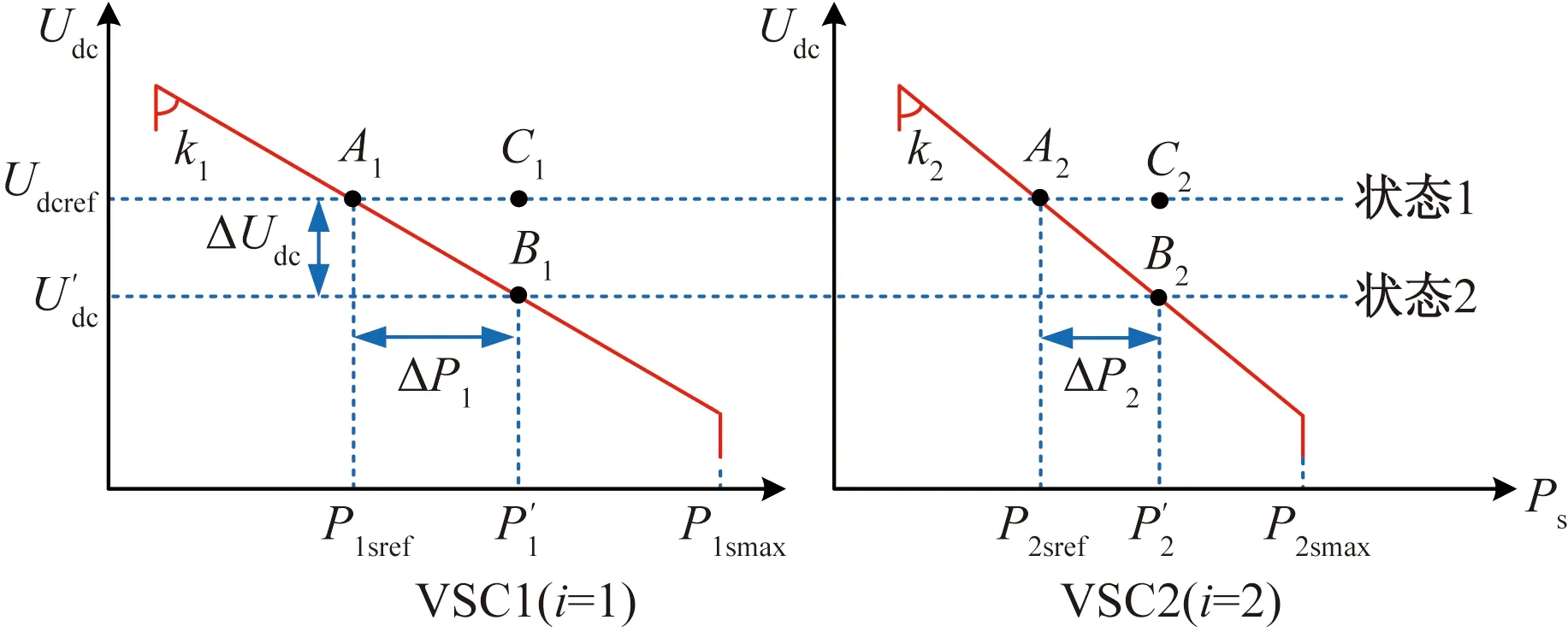
圖4 直流電壓下垂控制特性圖Fig.4 DC voltage droop control characteristic diagram

在穩態情況下,由圖3可得換流站直流電壓與有功功率的關系為

Udc=Udcref+k(Ps-Psref)

(2)

假設直流系統有N個換流站,其中1～m個換流站采用傳統下垂控制;m+1～n個換流站采用定有功功率控制,n+1～N個換流站采用定交流電壓控制。

1～m個下垂站有功功率參考值之和Pr為

(3)

式(3)中:1≤i≤m。

m+1～n個定功率站有功功率之和Pt為

(4)

式(4)中:m+1≤b≤n。

n+1～N個定交流電壓換流站有功功率之和Pw為

(5)

式(5)中:n+1≤j≤N。

根據圖4,設初始穩態時,系統運行在狀態1,當直流系統出現功率擾動ΔP時,m個下垂站利用自身下垂特性消納不平衡功率的同時,系統穩定運行點也會隨之移動。當再次達到穩態時,設系統運行在狀態2,此時直流電壓偏差為ΔUdc。由圖4可知,下垂站i所承擔的不平衡功率ΔPi與直流電壓偏差ΔUdc存在以下關系

(6)

根據能量守恒,各個下垂站有功功率變化量之和應等于ΔP,即

(7)

聯立式(6)與式(7),可得

(8)

(9)

由式(8)可以看出,ΔUdc與ΔP成正比,與m個下垂站的下垂系數倒數之和成反比。這說明,當直流系統功率發生波動后,所有下垂站會根據自身下垂曲線,協同消納不平衡功率[18]。

由式(9)可以看出,下垂系數決定了下垂站在動態調節過程中所承擔的不平衡功率的多少。若各換流站采用相同的下垂系數,則所有換流站均分不平衡功率;若各換流站采用不同的下垂系數,則下垂系數較小的換流站將承擔較多的不平衡功率,下垂系數較大的換流站將承擔較少的不平衡功率[19]。

2 改進的多點直流電壓協調控制策略

2.1 改進下垂控制

針對換流站采用傳統下垂控制消納不平衡功率固有的直流電壓偏差問題,提出一種改進的VSC-MTDC系統多點直流電壓優化協調控制策略,將不平衡功率作為前饋補償量注入下垂控制中,通過平移下垂曲線來實現直流電壓的準無差調節。優化協調控制策略的特性曲線如圖5所示。

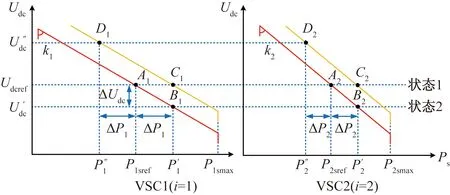
圖5 優化協調控制原理圖Fig.5 Optimization of coordinated control schematic diagram

設初始穩態時,系統運行在狀態1,當直流系統出現功率擾動ΔP時,給各個下垂站一個前饋補償量,大小為ΔPi。此時系統穩定運行點從Ai變為Di,實現下垂曲線的平移。Pisref和P″i分別為換流站調整前后的有功功率參考值,滿足

P″i=Pisref-ΔPi

(10)

而后換流站根據下垂特性消納不平衡功率,最終系統穩定運行在Ci點附近,實現直流電壓的準無差調節。與傳統下垂控制相比,換流站傳輸的有功功率并沒有發生改變,而直流電壓偏差近似為零,系統的穩定性得到大幅提高。

2.2 功率平衡分配方案

為了將直流系統中的不平衡功率合理分配給各個下垂站,將換流站的可用功率裕度引入功率分配系數上,快速調整有功功率參考值[20]。

P″i=Pisref-(Pimax-Pisref)×

(11)

式(11)中:Δt為系統采樣時間。在該功率平衡分配方案下,控制系統只需采集非下垂站的有功功率值,當且僅當直流系統潮流發生變化時,才向下垂站更新有功功率參考值。其余情況下,下垂站只需根據最近一次更新的有功功率參考值穩定運行。同時該功率平衡分配方案對站間通信要求極低,即使當各換流站通信中斷時,仍能按傳統下垂控制方式正常運行。

2.3 直流電壓偏差下垂控制

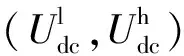
(12)

式(12)中:kb為直流電壓偏差下垂系數;Pbmax為定功率站的最大容量。

定功率站采用偏差下垂控制,在直流電壓超過設定的運行范圍時,設直流系統中余下的不平衡功率為ΔP*。當系統再次達到平衡時,采用偏差控制換流站的有功功率為

(13)

式(13)中:P′b為系統穩定后采用偏差控制換流站的有功功率。

對于圖1所示的五端系統,VSC1和VSC2采用優化下垂控制,VSC3和VSC4采用直流電壓偏差下垂控制,VSC5采用定交流電壓控制。系統控制特性曲線如圖6所示。

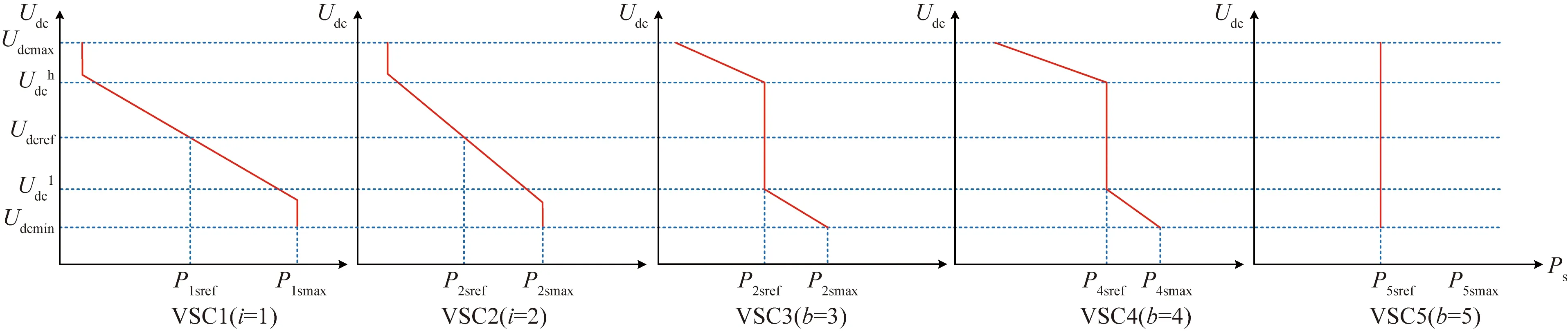
圖6 系統控制特性曲線Fig.6 The overall control characteristic curve of the system

3 仿真與分析

基于PSCAD/EMTDC仿真軟件搭建了如圖1所示的五端VSC-MTDC系統,具體仿真參數見表1。通過3個仿真算例,利用3種控制方法對比,驗證所提控制策略的有效性。

表1 系統仿真參數Table 1 System simulation parameters

控制方法1(CM1):傳統下垂控制。

控制方法2(CM2):優化協調控制。

控制方法3(CM3):優化協調控制+偏差下垂控制。

3.1 直流網絡出現功率盈余

t=3 s時,VSC3有功功率指令值由115 MW增至185 MW,仿真結果如圖7所示。

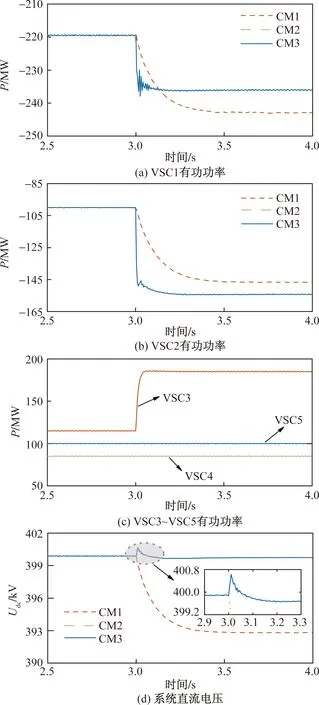
圖7 系統功率增加仿真Fig.7 System power increase simulation

由圖7可以看出,由于系統存在損耗,所以換流站有功功率、系統直流電壓實際值與參考值之間略有差別。設ΔP1～ΔP5為VSC1～VSC5有功功率變化量。t=3 s時,直流系統出現功率盈余,在CM1作用下,VSC1和VSC2按照傳統下垂控制消納不平衡功率,當系統達到穩態時,ΔP1和ΔP2分別為23.5 MW和46.5 MW,ΔUdc為7.09 kV,直流電壓偏差率為1.77%。在CM2作用下,ΔP1和ΔP2分別為16 MW和54 MW,ΔUdc為0.14 kV,直流電壓偏差率為0.035%,實現了直流電壓的準無差調節;同時系統將較多的不平衡功率分配給功率裕度較大的換流站,所以VSC2承擔的不平衡功率多于VSC1,避免VSC1滿載。由于直流電壓未超過系統設定的運行范圍,所以CM3作用下的仿真結果與CM2相同。

3.2 直流網絡出現功率缺損

t=3 s時,VSC3有功功率指令值由115 MW降至45 MW,仿真結果如圖8所示。

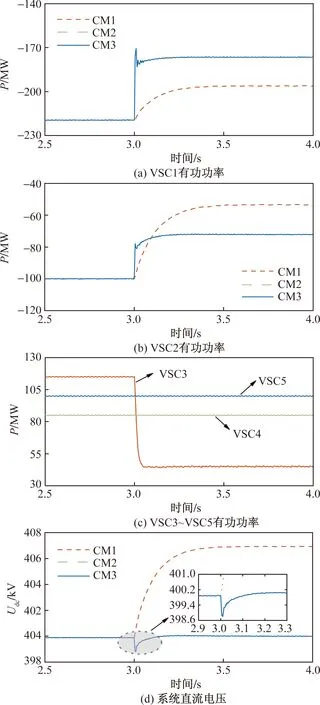
圖8 系統功率減小仿真Fig.8 System power decrease simulation

t=3 s時,直流系統出現功率缺損,由圖8可以看出,在CM1作用下,ΔP1和ΔP2分別為23.5 MW和46.5 MW,ΔUdc為7.03 kV,直流電壓偏差率為1.76%。在CM2作用下,ΔP1和ΔP2分別為42 MW和28 MW,ΔUdc為0.11 kV,直流電壓偏差率為0.028%。此時VSC1的功率裕度多于VSC2,所以VSC1承擔的不平衡功率多于VSC2。

3.3 換流站退出

t=3 s時,VSC2退出運行,仿真結果如圖9所示。可以看出,在CM1作用下,VSC1作為唯一的功率平衡點,很快達到滿載并切換成定有功功率運行,失去了控制直流電壓的能力,直流電壓將繼續下降。在CM2作用下,由于VSC3和VSC4控制方式仍然為定有功功率,并不參與系統功率的調節,所以ΔP3和ΔP4都為0 MW。在CM3作用下,在直流電壓下降至390 kV時,VSC3和VSC4由定有功功率控制轉變為下垂控制,協同VSC1消納不平衡功率,承擔起穩定直流電壓的任務。在系統進入穩態后,ΔP1、ΔP3和ΔP4分別為26、41和33 MW,ΔUdc為14.49 kV,直流電壓偏差率為3.62%。同時VSC1并沒有達到滿載,還具備穩定直流電壓的能力,系統的穩定性得到了較大的提高。

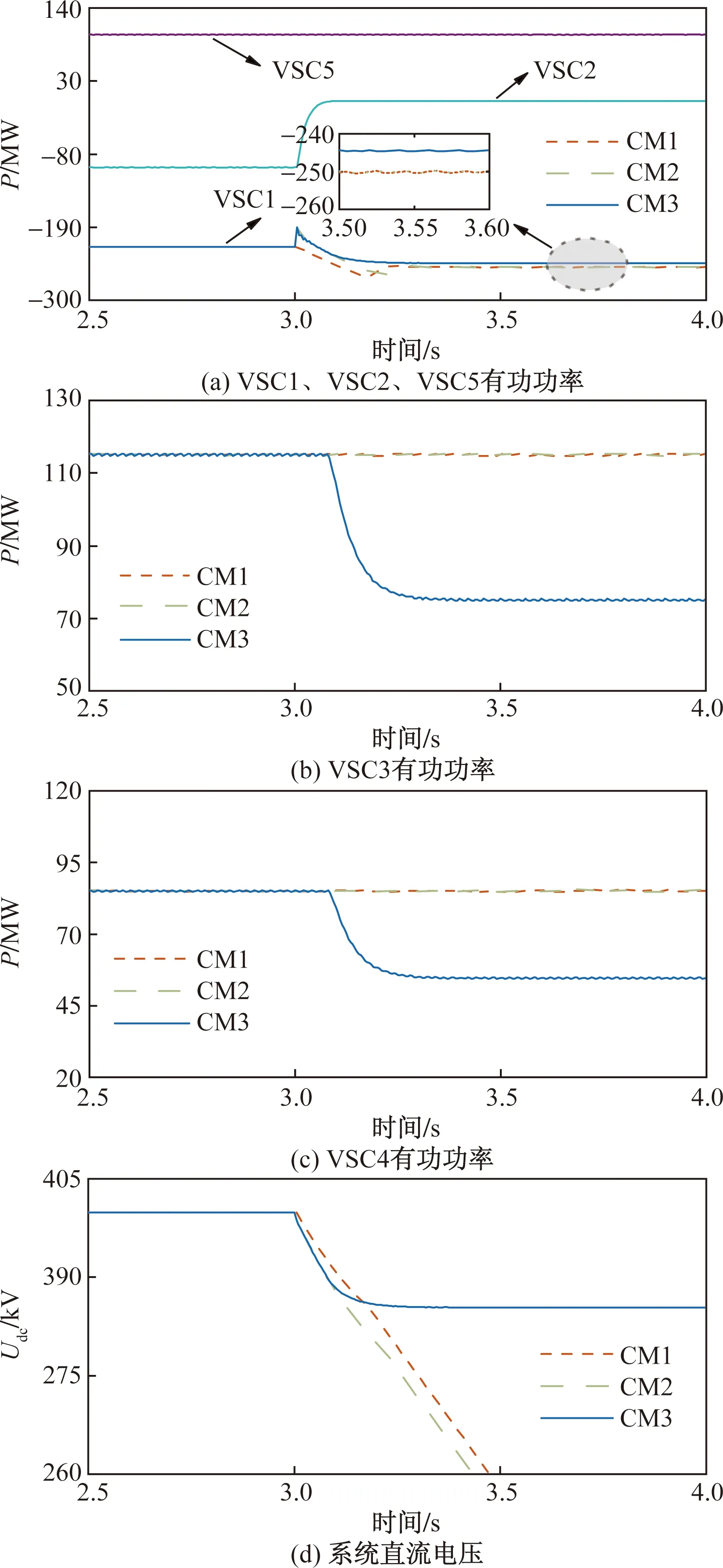
圖9 換流站退出仿真Fig.9 Simulation of converter station exit

4 結論

針對換流站采用傳統下垂控制消納不平衡功率時固有的直流電壓偏差問題,提出一種改進的VSC-MTDC系統多點直流電壓優化協調控制策略,結論如下。

(1)通過前饋補償換流站有功功率參考值,平移下垂曲線,可以實現直流電壓的準無差調節。

(2)根據換流站功率裕度分配不平衡功率,可以有效避免部分換流站過載而其他換流站還余有功率裕度的情況發生。

(3)通過將偏差下垂控制引入定功率站,提高了系統在不平衡功率較大時的運行穩定性。