基于遺傳算法的公路自動選線與安全評價方法

朱雷鵬, 張貴陽, 張志清*

(1.北京工業(yè)大學城市交通學院交通工程北京市重點實驗室, 北京 100124; 2.中國電建市政建設集團有限公司, 天津 300384)

目前,中國公路選線設計體系依賴于專家經驗知識,基于公路選線設計規(guī)范標準,通過試湊法,從備選方案中比選出一條符合標準的線路[1-2]。但公路選線需要統(tǒng)籌考慮大量的影響因素,是一項復雜的系統(tǒng)工程,而傳統(tǒng)人工選線方法設計的備選方案有限,選線設計人員的經驗程度不同,很難找出全局最優(yōu)或者接近最優(yōu)的公路路線設計方案,并且容易漏掉優(yōu)秀的選線方案,這在一定程度上降低了選線的效率與質量[3-4]。因此,提出一種能夠實現公路自動選線的智能化方法,是道路勘測設計領域亟須解決的科學問題之一。

自動選線可提升選線方案的質量與綜合決策效率,是一種新型高效的線形設計方法[5]。隨著計算機技術的發(fā)展,國內外學者提出了大量自動選線尋優(yōu)方法。主要有距離變換法、網絡自適應直接搜索、遺傳算法等。其中,距離變換法和網絡自適應直接搜索可結合選線經驗,在地形簡單的平原、丘陵地區(qū)實現自動選線,但在復雜地形環(huán)境下難以得到可行的選線結果[6]。而遺傳算法具有高效的全局搜索能力與求解速度,可處理復雜的非線性約束,已在自動選線研究中得到了廣泛應用[7-8]。其中,You等[9]基于遺傳算法,構建了以線路設計規(guī)范為約束,以經濟性、安全性為目標函數的線形優(yōu)化模型,選線結果有利于提高公路安全性,減少選線工作人員的冗余調試工作。李成謙等[10]通過識別諸多線形設計參數中的風險因素,構建了基于成本-安全均衡的自動選線模型,通過遺傳算法求解表明,該模型顯著提高了公路的安全性與成本效益,并在川藏高速公路工程中得到了應用與驗證。張馳等[11]基于遺傳算法,結合Rhino+Grasshopper平臺,構建了考慮風景環(huán)境的自動選線模型,緩解了既有自動選線方法在小區(qū)域范圍內選線結果不準確的難題。劉光偉等[12]引入分階段的選線剖面布置形式,結合線路幾何特性與工程費用,構建了露天煤礦自動選線模型,利用遺傳算法求解表明,相比于手工定線方法,優(yōu)化后的模型能夠快速、高效地找出費用最低的選線方案。同時,部分學者還構建了基于生態(tài)視角的公路自動選線模型,進一步豐富了公路自動選線的研究體系[13]。此外,為了探究更合理的路線評價方法,有學者認為有必要對公路平縱組合的安全性進行評價,進一步提升公路的選線效率與安全評價水平[14]。

綜上所述,既有基于遺傳算法的公路自動選線研究成果,主要集中在構建公路線形的表示方法和建立目標函數兩個方面,仍然存在不足。一是大部分研究將平面交點的選擇方式假定為等距分布,并在規(guī)定剖面上搜索其合理位置,而在實際選線過程中,公路平面交點位置應在選線區(qū)域內進行隨機搜索,該假設與實際情況并不相符;二是既有研究對選線方案的安全性評價仍待進一步完善。因此,現擬在重點考慮自動選線方案安全性的基礎上,建立基于遺傳算法的自動選線優(yōu)化模型,在選線區(qū)域內隨機搜索平面交點位置,力爭實現擬定選線區(qū)域路線方案的自動尋優(yōu)。

1 自動選線流程設計與路線表達

1.1 選線流程設計

遺傳算法是求解復雜優(yōu)化問題全局最優(yōu)解的有效算法[15-16]。基于遺傳算法的公路自動選線與安全評價方法流程如圖1所示。

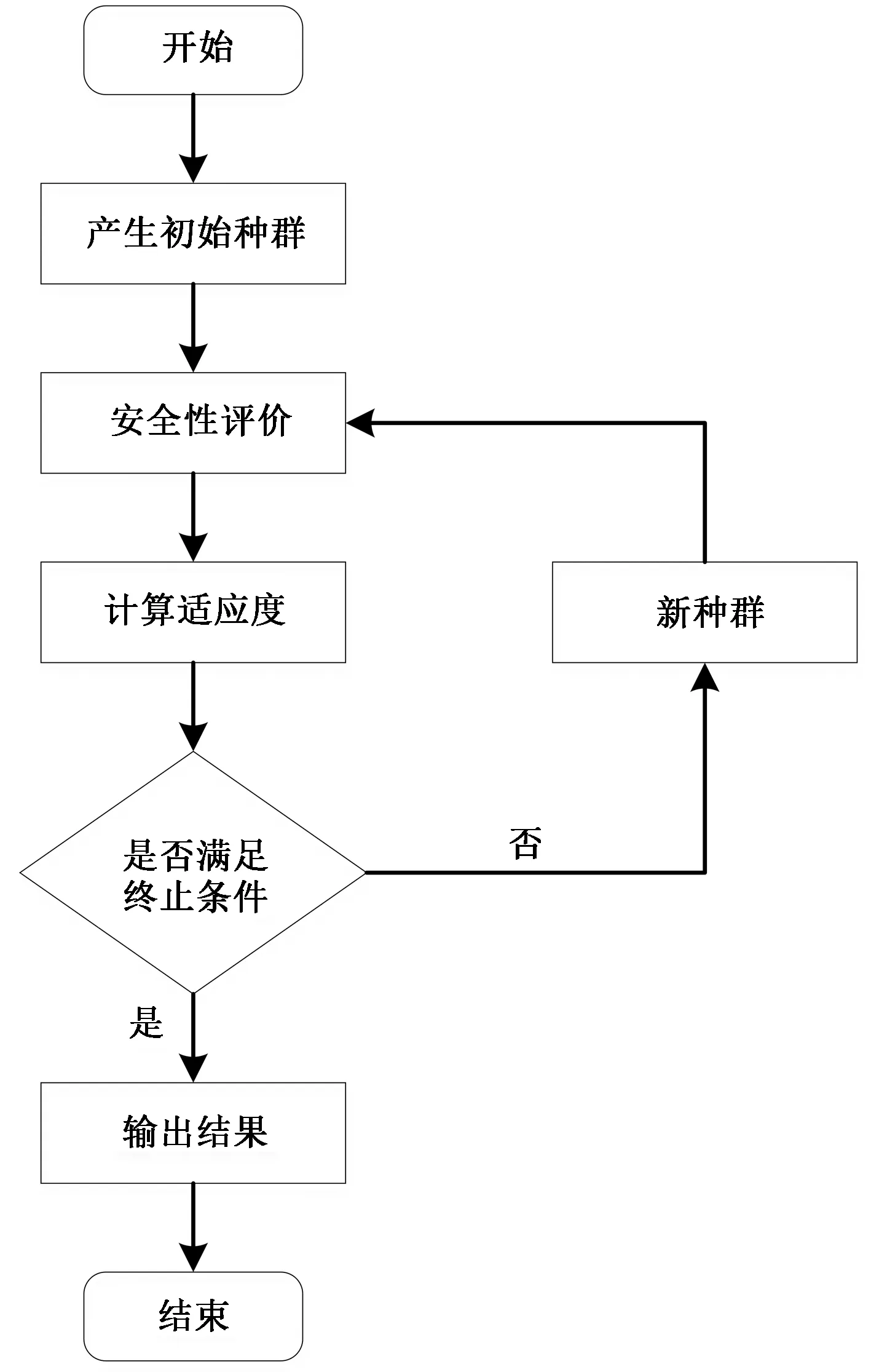
圖1 基于遺傳算法的公路自動選線與安全評價方法Fig.1 Highway automatic alignment selection and safety evaluation method based on genetic algorithm

1.2 公路路線表示

公路路線模型由平面和縱斷面線形組合而成,如圖2和圖3所示,假設S(XS,YS)、E(XE,YE)為路線的起終點,在起點S和終點E之間選擇n個不同的點作為路線交點,確定合適的平曲線半徑。為了便于研究,按《公路路線設計規(guī)范》(JTG D20—2017)(以下簡稱規(guī)范)選取固定長度的緩和曲線。公路線形優(yōu)化就是不斷搜索優(yōu)化路線交點位置、圓曲線半徑、豎曲線半徑及變坡點高程的過程。

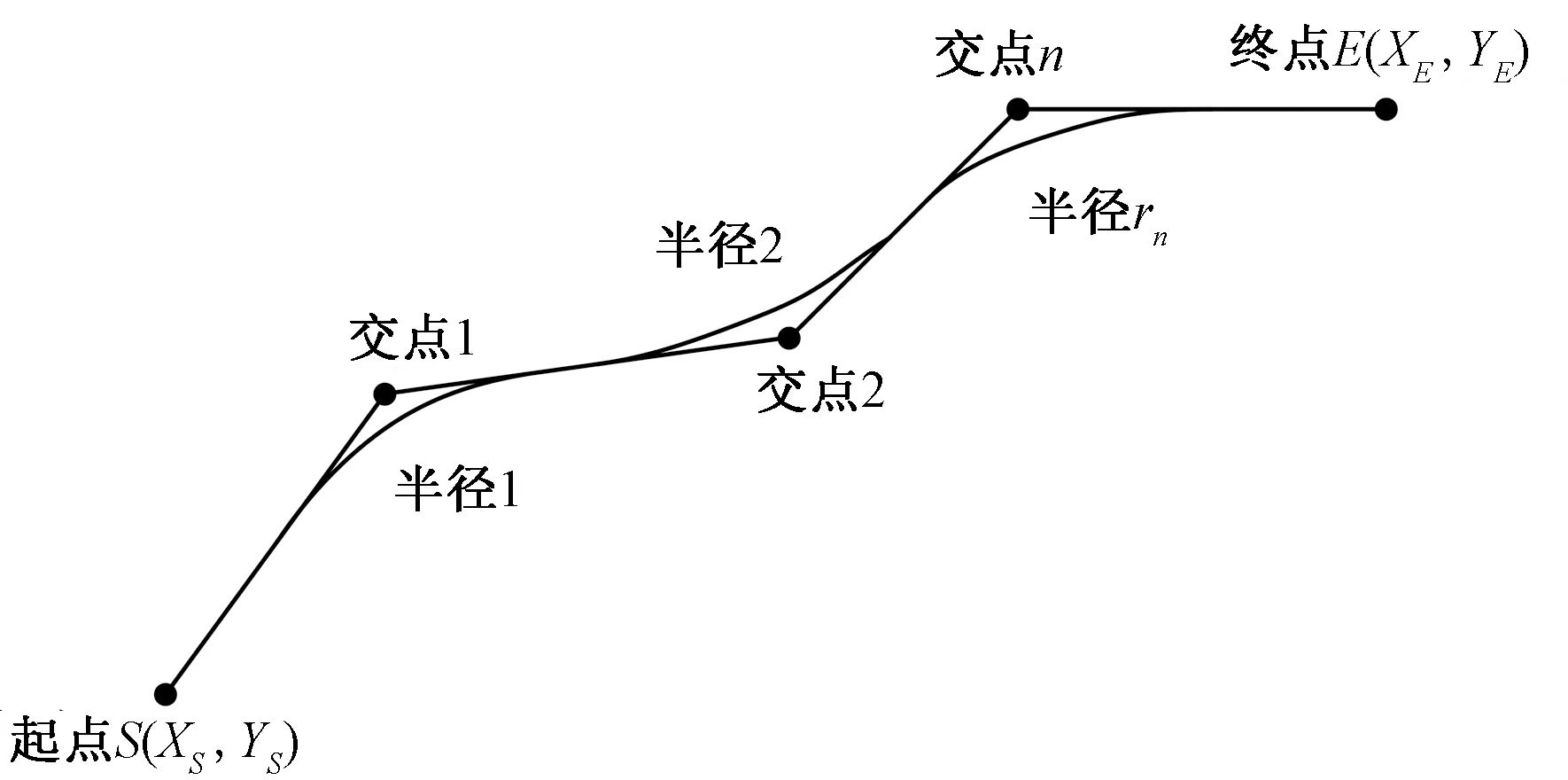
圖2 公路平面線形示意圖Fig.2 Schematic diagram of highway plane alignment

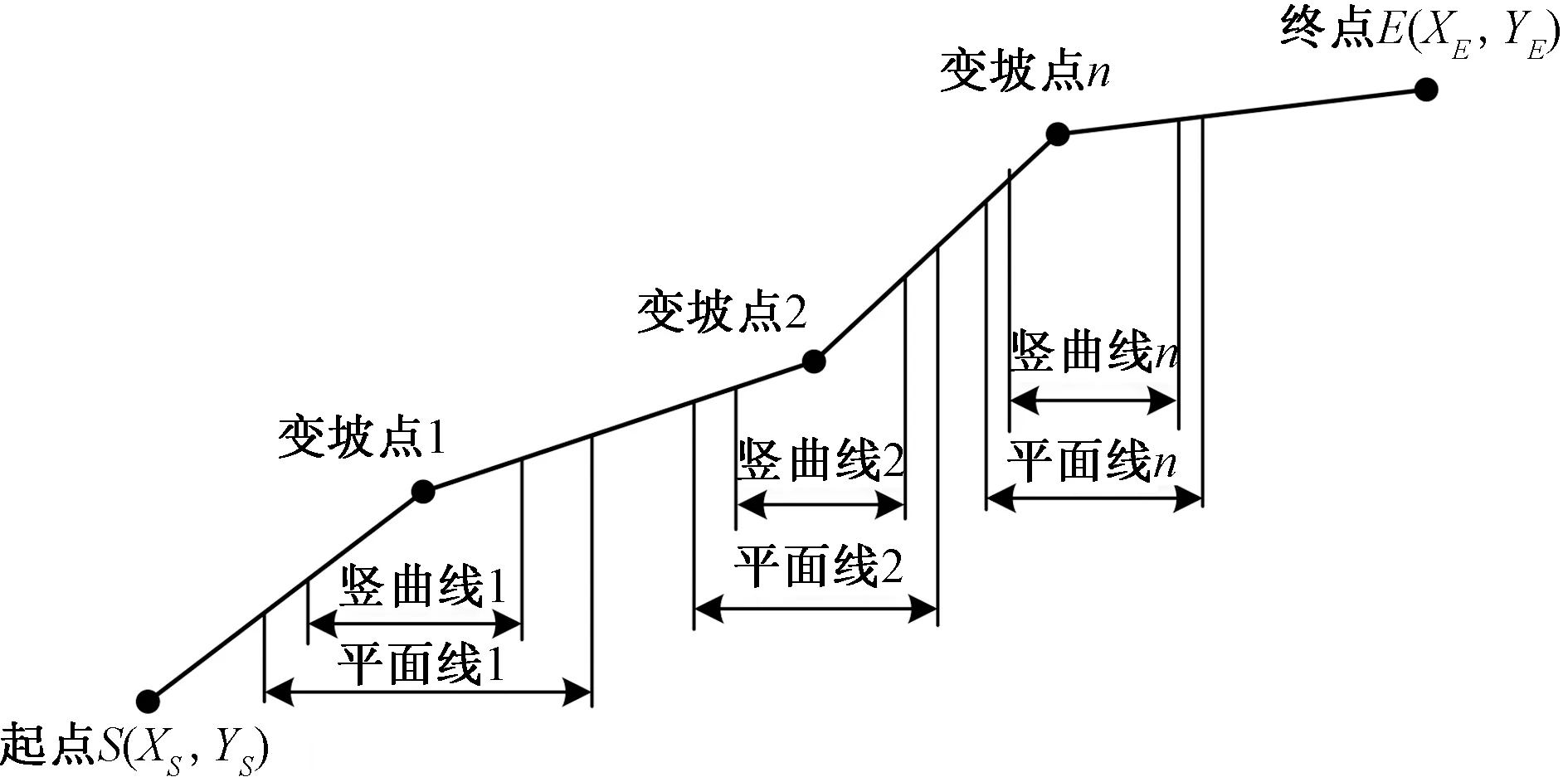
圖3 公路縱斷面線形示意圖Fig.3 Highway longitudinal section alignment schematic

2 公路線形約束模型

基于《公路路線設計規(guī)范》(JTG D20—2017),考慮公路平面、縱斷面以及平縱組合等關鍵線形技術參數,構建公路線形約束模型。

2.1 公路路線平面約束

路線平面約束主要包括路線的圓曲線半徑(R)、平曲線間夾直線長度(L)、直線長度(LZ)、平曲線長度(LC)等方面的約束。

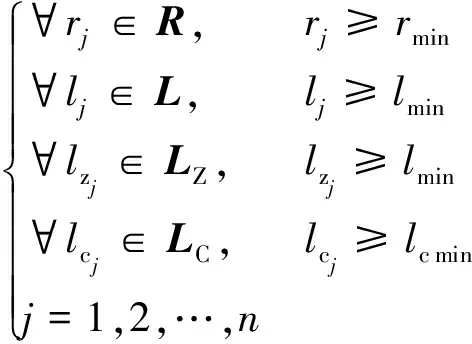
(1)

式(1)中,rj、lj、lzj、lcj分別為路段j圓曲線半徑、平曲線間夾直線長度、直線段長度以及平曲線長度的取值;rmin、lmin、lzj、lcmin分別為規(guī)范里對平面應線形參數的最小值。此外,平曲線間夾直線長度(lzj)在滿足規(guī)范的基礎上,為提高公路平面線形的平順性,還應符合式(2)的規(guī)定。

式(2)中:v為路段j的設計速度。

2.2 公路路線縱斷面約束

路線縱斷面約束主要包括路線的縱坡(I)及坡長(LD)等方面的約束。

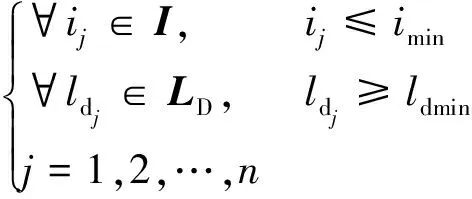
(3)

式(3)中:ij、ldj路段j坡度與坡長的取值;imin、ldmin分別依據設計速度從《公路路線設計規(guī)范》(JTG D20—2017)中進行取值,其中,imin≥0.3%。

2.3 公路路線平縱線形組合約束

為保證線形設計一致性及行車安全,公路自動選線要求豎曲線起點與終點在平曲線內。

3 路線基因編碼與初始方案生成

3.1 路線基因編碼

連續(xù)搜索選線區(qū)域,高效確定公路交點線形技術參數是實現公路自動選線的關鍵技術問題。在實數編碼中,不僅可以簡化編碼過程,還能夠保證路線方案的全局最優(yōu)性能,因此選擇實數編碼對公路三維空間基因編碼進行改進。公路自動選線基因編碼過程如圖4所示。

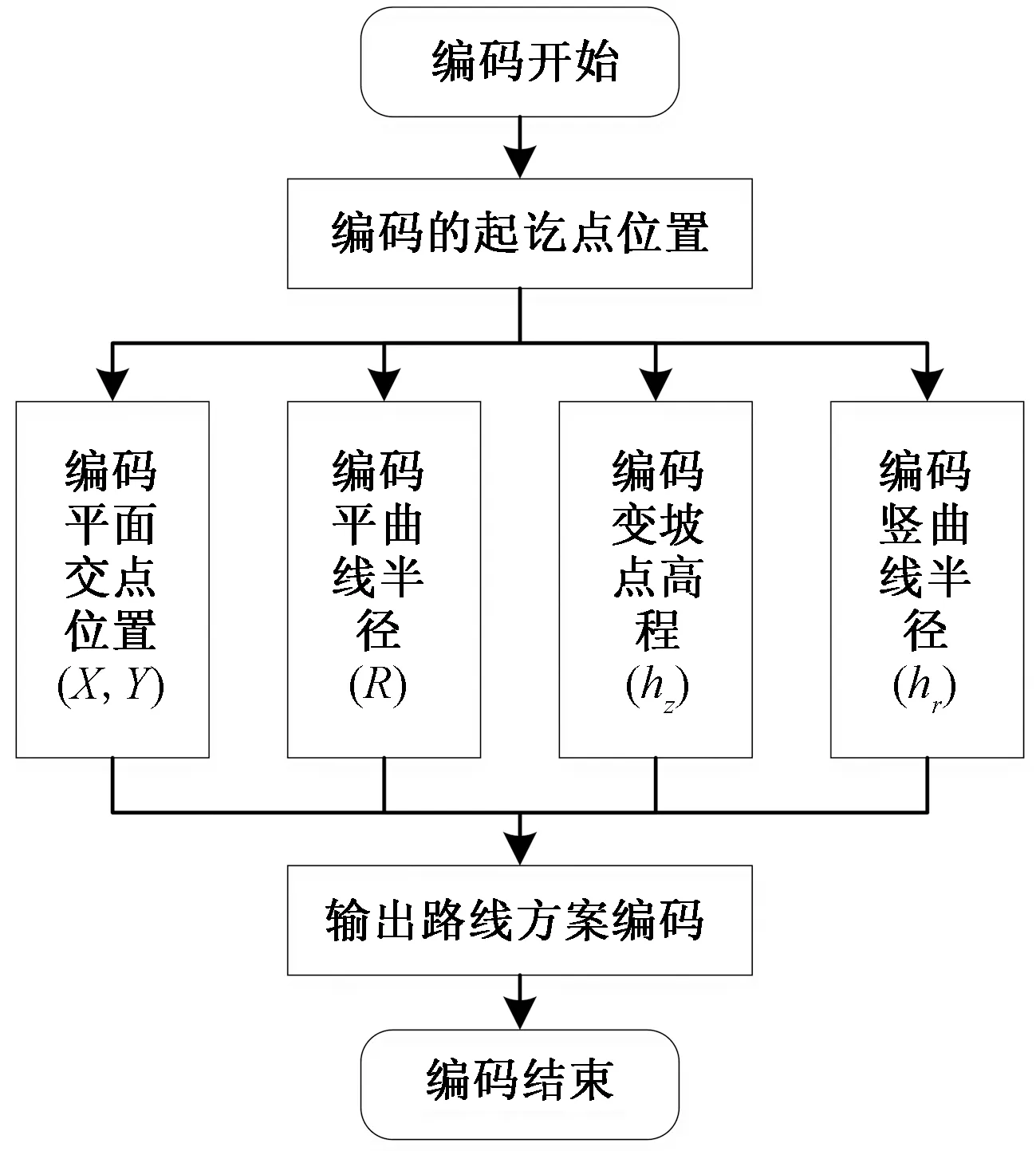
圖4 公路自動選線基因編碼過程示意圖Fig.4 Schematic diagram of the genetic coding process for automatic highway routing

實數編碼時,公路路線的基因編碼可以歸結為:平面交點坐標(X,Y)、圓曲線半徑(R)、變坡點高程(hz)、豎曲線半徑(hr)。則公路個體基因型為X、Y、R、hz、hr。其中X、Y、R、hz、hr均為n維向量,表示平面n個交點。

3.2 路線初始方案生成

根據公路路線方案的基因編碼,可以生成路線方案初始種群。首先隨機產生n個交點,然后再按照起點到終點之間的順序,在這n個點處布設直線、圓曲線和緩和曲線,最后加上豎曲線,組成一個初始路線方案。重復產生m個初始路線,便形成了包含m個體的初始方案種群。

4 路線適應度函數與遺傳算法

4.1 適應度函數

4.1.1 目標函數

選擇公路修建總費用(C)作為目標函數。公路修建總費用的計算公式為

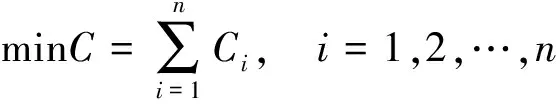
(4)

式(4)中:n為公路修建過程中費用的類別數;Ci為第i類具體費用(例如,拆遷補償、工程建設以及設備租賃等費用)。

4.1.2 適應度值

公路自動選線的目標是通過不斷計算目標函數,同步調整具體設計方案,以適應度值作為擇優(yōu)標準,對設計方案進行比選,從而在眾多方案中得到最優(yōu)方案,實現公路選線的自動優(yōu)化決策。適應度函數的計算公式為

fi=Cmax-Ci

(5)

式(5)中:fi為第i代選線方案的適應度值;Cmax=max(Ci)為各類費用的最大值。

4.2 遺傳算法實現自動尋優(yōu)

為了使路線能夠避開不利地形,實現智能設計調整路線位置與平縱線形關鍵技術參數,基于遺傳算法通過設計選擇算子、交叉算子及變異算子實現公路路線及線形關鍵技術參數的不斷尋優(yōu)。為了保證選線方案的不斷優(yōu)化和保留每一代優(yōu)化方案,在遺傳算法模型中采用最佳個體保留法,將每一代中適應度最高的5個選線方案作為基礎方案參與子代的迭代過程。

5 公路安全性評價

平縱線形滿足技術規(guī)范標準的路線也不一定滿足舒適、安全的行車需要,因此有必要檢驗其安全性能[17]。利用遺傳算法得到的平縱線形技術參數,預測各路段運行速度,以相鄰路段之間運行速度的差值作為公路線形設計與運營一致性的評價指標,評價選線方案中關鍵線形參數的合理性。

5.1 尋優(yōu)路段分類

根據公路線形的不同平縱組合,將整條公路劃分為4種形式,路段劃分標準如表1所示。

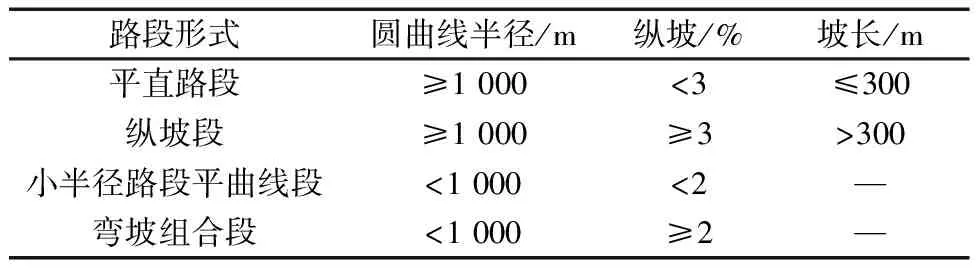
表1 路段劃分標準

5.2 運行速度測算

選取二級公路為研究對象,確定車輛類型為小汽車,基于遺傳算法每一代產生的選線方案中平縱線形技術參數,對各路段運行速度進行預測。

5.2.1 平直路段

在平直路段,視距和線形條件通常較好,駕駛人員為獲得更好的駕駛體驗,往往想達到期望速度,當行駛速度低(高)于期望速度時,會發(fā)生加(減)速行為。直線路段出口處的運行速度按式(6)測算。

ifv0=vpre

thenvout=v0;

else ifv0≠vpre

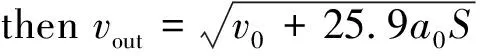
(6)

式(6)中:v0、vout、vpre分別為直線路段入口處的入口速度、出口速度及運行速度,其中v0取80 km/h;a0為汽車的加速度,當a0>0時,a0∈[0.15,0.5]m/s2;當a0<0時,a0∈[-0.5,-0.15]m/s2;S為直線路段的長度,km。

5.2.2 縱坡路段

縱坡路段的運行速度主要受坡度與坡長的制約,可忽略由平面線形帶來的影響,因此以坡度和坡長為約束條件對縱坡路段的入口速度進行修正。縱坡段運行速度修正標準如表2所示。

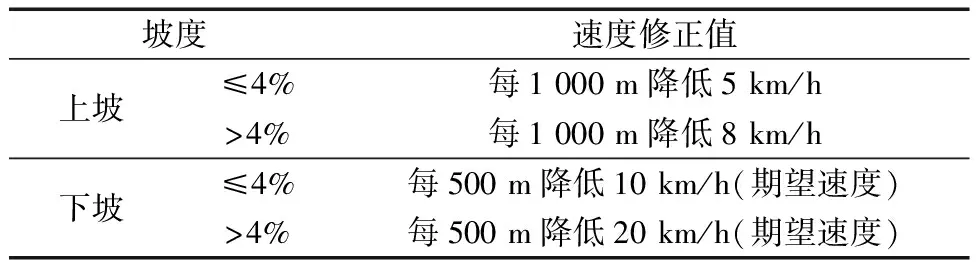
表2 縱坡段運行速度修正標準

5.2.3 小半徑平曲線路段

小半徑平曲線段的運行速度按式(7)測算[18]。

vout=12.26+0.83v0+5.73R

(7)

式(7)中:R為平曲線半徑,km。

5.2.4 彎坡組合路段

彎坡組合路段的運行速度按式(8)測算[18]。

vout=-4.38+0.55v0+0.72vmiddle+11.71lnR+0.18Inow1-1.44Inow2

(8)

式(8)中:vmiddle為車輛在平曲中點處的運行速度,km/h;Inow1、Inow2分別為平曲線段前(后)直線坡度,%。

5.3 評價指標

相鄰路段運行速度的差值(Δv85)是衡量道路線形設計安全性的重要指標[19]。基于Δv85設計道路線形一致性評價流程,如圖5所示。

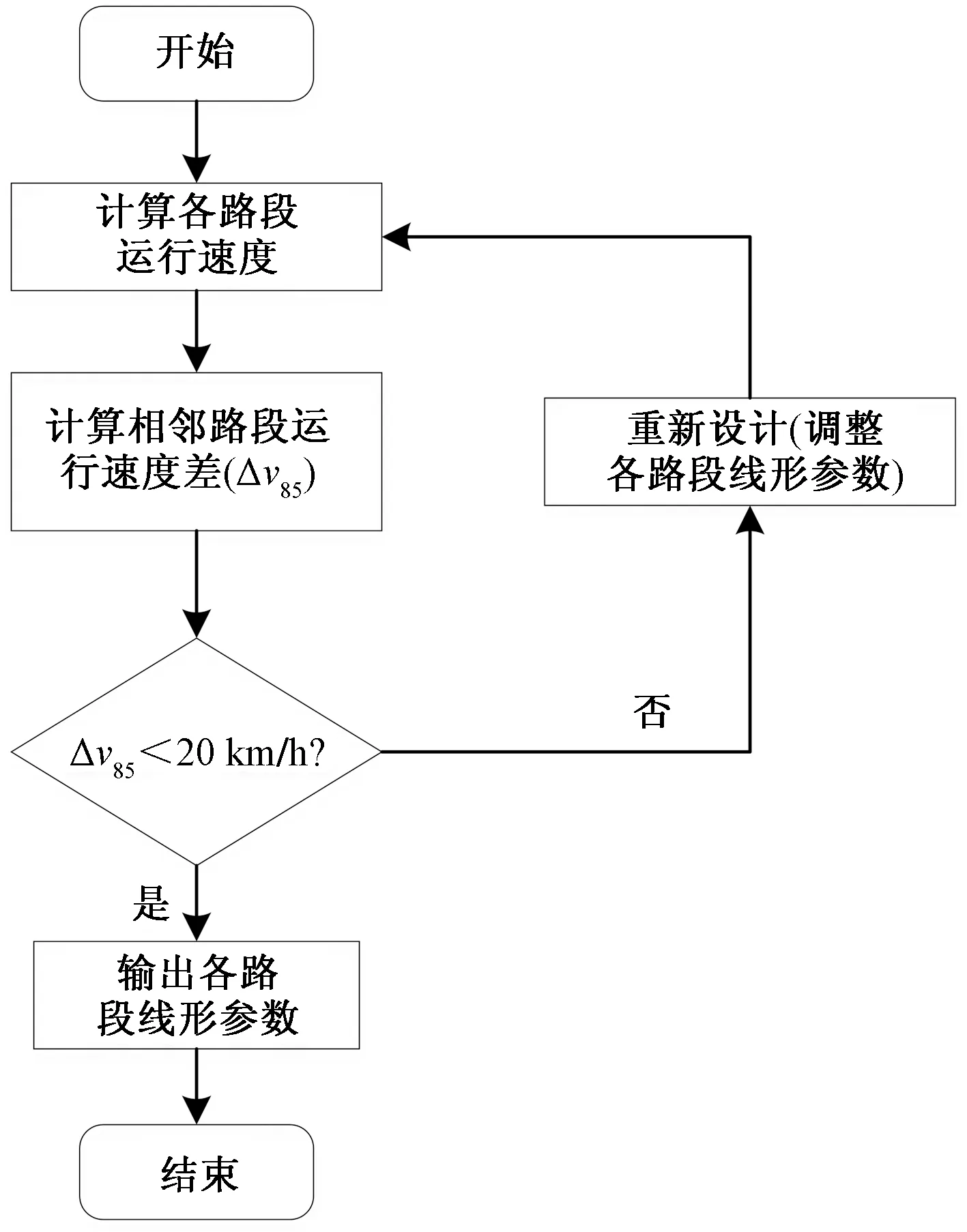
圖5 基于Δv85的道路線形安全性評價流程Fig.5 Road alignment safety evaluation process based on Δv85

6 選線實例

6.1 選線區(qū)域介紹及算例參數取值

6.1.1 選線區(qū)域介紹

為了驗證算法的可行性,以北京市黃松峪地區(qū)為自動選線試驗區(qū)域,以實現公路路線的自動搜索和優(yōu)化。黃松峪地處北京市平谷區(qū),地勢北高南低,海拔在100～120 m,所選區(qū)域選線區(qū)域起訖點坐標分別為:S(477 772.98, 320 625.08)、E(478 204.23, 321 791.85)。

6.1.2 算例參數取值

進行算例參數取值前,已對研究區(qū)域的地形、地質、人文及水文等影響公路路線走向的因素進行了前期調查,并對數據進行了轉換處理。參考《公路路線設計規(guī)范》(JTG D20—2017),對公路線平面、縱斷面及橫斷面關鍵技術參數進行了取值,公路路線基本參數如表3所示。同時對遺傳算法基本參數進行取值,遺傳算法基本參數如表4所示。

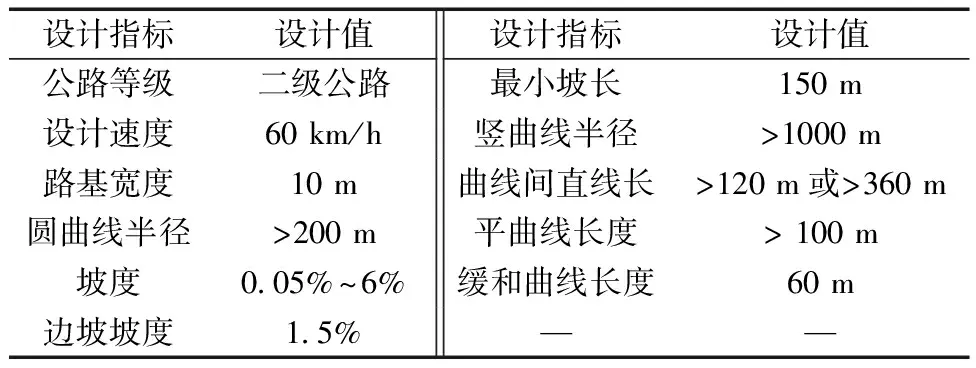
表3 公路路線線形基本參數

表4 算法基本參數

為實現自動選線,在選線區(qū)域產生2個平面交點以生成公路選線初始方案群,公路初始種群適應度值示例如表5所示。

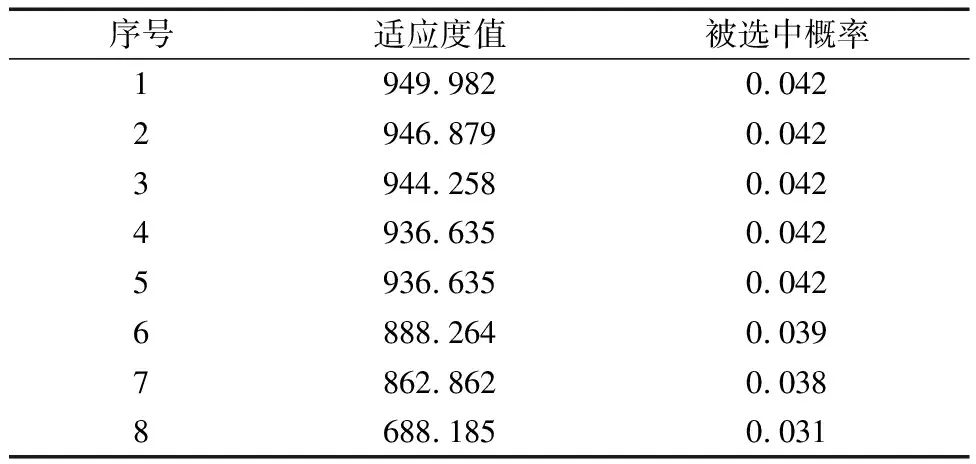
表5 公路初始種群適應度值示例

6.2 選線結果分析

結合公路線形平面、縱斷面、平縱組合技術指標約束條件,設計遺傳算法,在對每代選線方案進行安全性評價的基礎上,輸出每一代公路自動選線的路線長度、總費用的最優(yōu)結果,每一代路線基本信息如表6所示。每一代最優(yōu)路線總費用、每一代最優(yōu)路線長度分別如圖6、圖7所示。

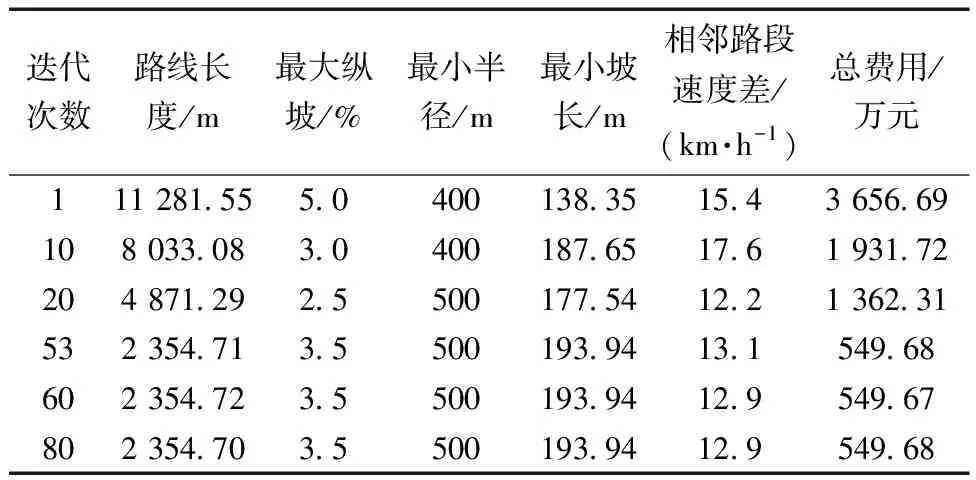
表6 每一代路線基本信息表

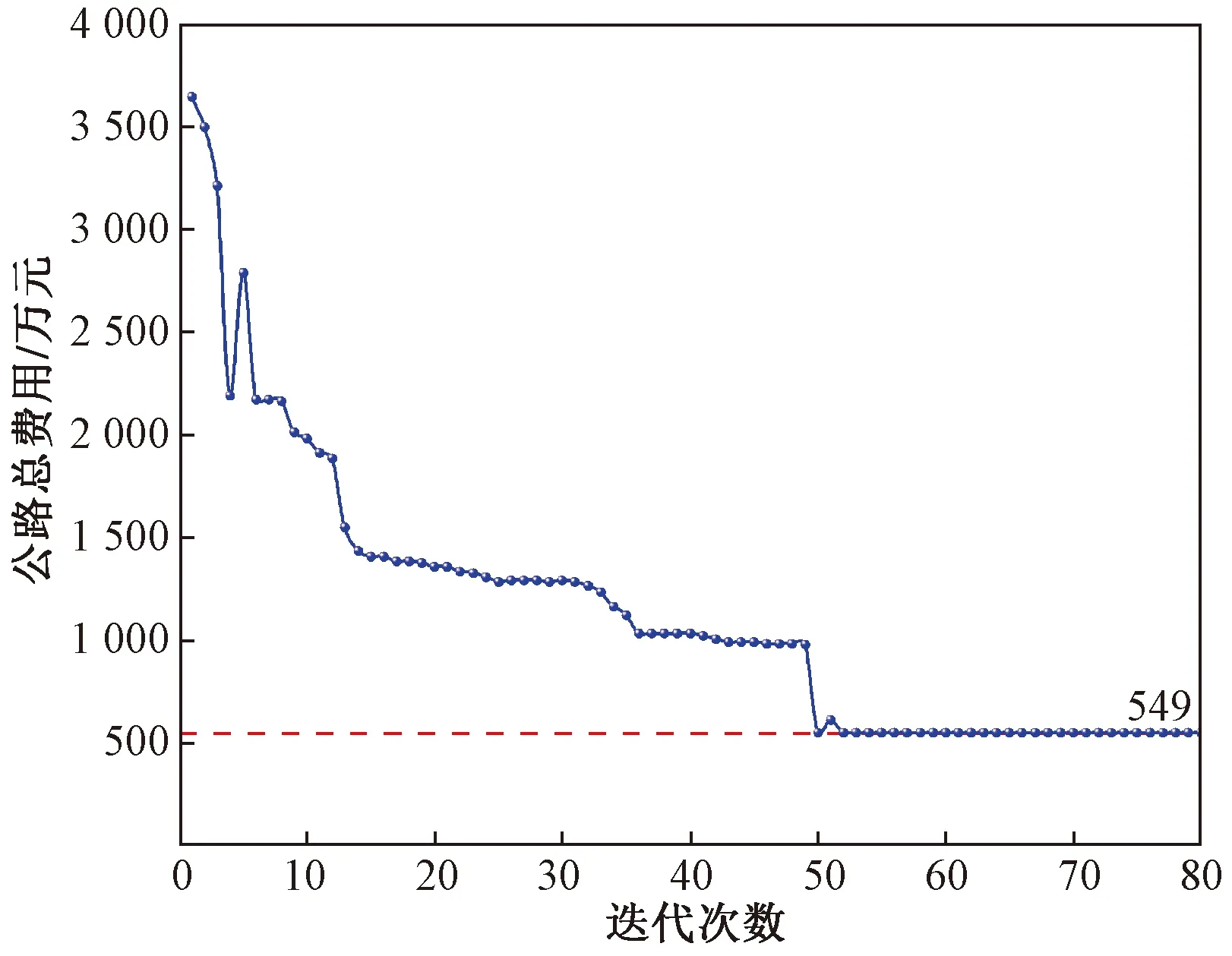
圖6 每一代最優(yōu)路線總費用迭代圖Fig.6 Iteration chart of total cost of optimal alignment of each generation

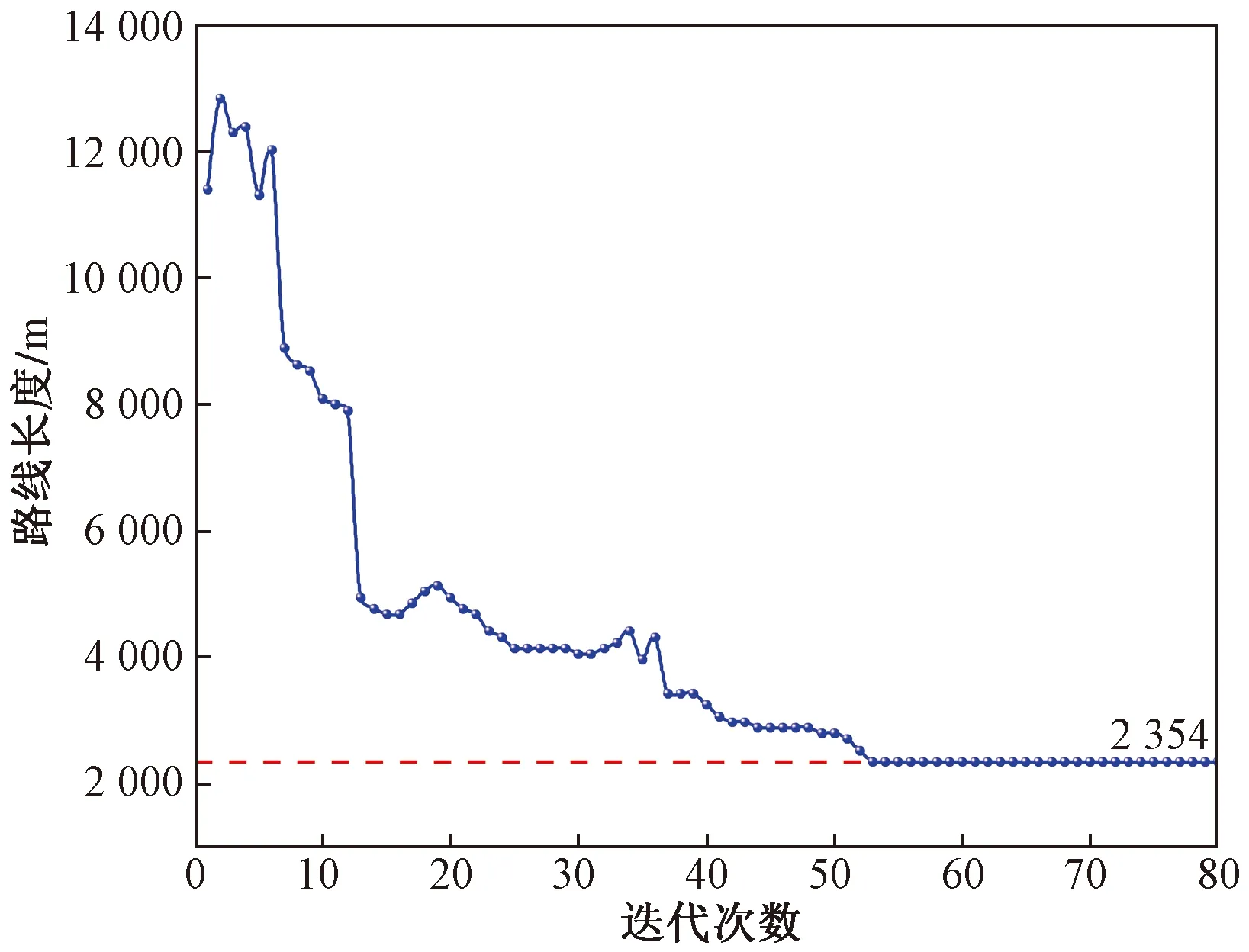
圖7 每一代最優(yōu)路線長度變化圖Fig.7 Iteration chart of total cost of each generation of optimal alignment and change chart of length of each generation of optimal alignment

由表6可得,相鄰路段的速度差均小于 20 km/h,符合公路選線線形安全性標準,表明所引入的運行速度預測模型,可以滿足公路選線方案的安全性審查要求。同時,最大縱坡、最小半徑、最小坡長均滿

足公路線形約束條件,表明基于遺傳算法設計的公路自動選線與安全評價方法能夠滿足公路選線基本規(guī)范的要求,可作為公路自動選線的優(yōu)化方法。

由圖6和圖7可知,公路路線的工程總費用變化趨勢與路線長度變化基本相似,工程總費用的變化更能體現公路自動選線優(yōu)化的特點,迭代初始迅速優(yōu)化,迭代中期優(yōu)化速度放慢,接著優(yōu)化速度趨于平緩,最后保持不變。說明隨著迭代次數的不斷增加,選線方案在公路路線平面、縱斷面、平縱組合的約束條件下逐漸趨于最優(yōu),與現實情況相符,表明本文構建的模型,能夠在保證公路線形安全的基礎上,得到全域最優(yōu)的選線方案。迭代至第53代,在滿足平面線形技術標準要求及安全性標準的條件下,選線方案達到最優(yōu),并得到關鍵線形技術參數。其中,線路長度為2 354.71 m、最大坡度為3.5%、最小曲線半徑為500 m、最小坡長為193.94 m、相鄰路段速度差為13.1 m/s、總費用為549.68 萬元,選線方案達到了最優(yōu)。

綜上,基于遺傳算法的公路自動選線模型,在考慮路線安全性條件下,可以同時保證路線交點在擬定的選線區(qū)域全局進行自動搜索,驗證了公路自動選線方法的可行性,可以實現公路路線的自動選擇和優(yōu)化,能夠顯著提高公路選線的工作效率。

7 結論

針對現有公路選線模型在平面交點確定方法與安全性評價等方面問題,基于遺傳算法,建立了路線優(yōu)化模型,并設計了公路安全性評價方案,基本實現了公路選線方案的自動尋優(yōu)和主動安全評價。

(1)基于遺傳算法,分別從公路平面、縱斷面以及平縱組合3個方面構建了公路路線約束模型,從安全性和經濟性層面選取指標作為選線方案評價標準,建立了公路自動選線優(yōu)化模型。

(2)通過在選線區(qū)域內隨機設置公路路線的平面交點,實現了選線全域范圍內所有選線方案的自動優(yōu)劣比較,保證了所選公路路線方案的全局域最優(yōu),提升了選線方案的決策效率,彌補了傳統(tǒng)選線方法的不足。

(3)將相鄰路段的運行速度差作為評價線形安全的理念引入現代公路設計體系,構建了運行速度預測模型,與傳統(tǒng)直接依據公路設計標準規(guī)范設計的選線方案相比,可提升公路選線方案的安全等級與經濟效益。