水驅(qū)砂巖油藏儲(chǔ)層物性時(shí)變規(guī)律分析方法綜述

謝倩, 劉尚奇, 王瑞峰, 楊軒宇

(中國(guó)石油勘探開(kāi)發(fā)研究院, 北京 100083)

自20世紀(jì)90年代,已有學(xué)者對(duì)注水開(kāi)發(fā)模式下油藏儲(chǔ)層動(dòng)態(tài)變化開(kāi)展了大量研究工作,注入水的長(zhǎng)期浸泡和沖刷作用使儲(chǔ)層中的巖石顆粒、黏土礦物等發(fā)生物理化學(xué)反應(yīng),導(dǎo)致儲(chǔ)層參數(shù)發(fā)生變化[1-2],形成局部?jī)?yōu)勢(shì)滲流通道,注入水沿優(yōu)勢(shì)通道無(wú)效或低效循環(huán),平面、層間及層內(nèi)矛盾加劇[3-4],剩余油分布整體高度分散、局部相對(duì)富集,地下滲流場(chǎng)較開(kāi)發(fā)初期發(fā)生很大變化[5],依據(jù)初始儲(chǔ)層物性參數(shù)已不能有效指導(dǎo)開(kāi)發(fā)后期工作。

縱觀有關(guān)儲(chǔ)層物性時(shí)變分析與應(yīng)用相關(guān)文獻(xiàn),對(duì)于如何有效定量表征儲(chǔ)層參數(shù)變化規(guī)律,早期主要為儲(chǔ)層物性變化機(jī)理研究,逐漸側(cè)重儲(chǔ)層微觀及宏觀參數(shù)變化特征,但仍以定性為主,后發(fā)展到半定量、定量研究[4-13],將定量的物性時(shí)變規(guī)律引入主流數(shù)值模擬軟件,實(shí)現(xiàn)數(shù)值模擬精細(xì)化應(yīng)用。該研究的重點(diǎn)是明確不同地質(zhì)和開(kāi)發(fā)因素對(duì)儲(chǔ)層參數(shù)影響的定量規(guī)律,建立動(dòng)態(tài)地質(zhì)模型,實(shí)現(xiàn)油田實(shí)際應(yīng)用。目前多數(shù)研究方法存在考慮影響因素有限,且依賴取心資料,而一孔之見(jiàn)難以代表全區(qū)域,人為主觀影響較大,以及宏觀與微觀物性變化研究缺乏明確聯(lián)系等難點(diǎn)。現(xiàn)通過(guò)分別對(duì)儲(chǔ)層微觀、宏觀物性參數(shù)時(shí)變研究方法及現(xiàn)狀進(jìn)行梳理和分類總結(jié),以期啟發(fā)相關(guān)研究者利用新手段建立微觀與宏觀參數(shù)量化關(guān)系,綜合研究不同地質(zhì)、流體、開(kāi)發(fā)因素下的儲(chǔ)層參數(shù)時(shí)變規(guī)律。在此基礎(chǔ)上精確模擬和預(yù)測(cè)水驅(qū)油藏優(yōu)勢(shì)滲流通道及剩余油分布,從而對(duì)油田后期分層注水、優(yōu)化措施等精細(xì)化開(kāi)發(fā)具有重要指導(dǎo)意義。

1 儲(chǔ)層微觀物性時(shí)變規(guī)律研究現(xiàn)狀

1.1 室內(nèi)實(shí)驗(yàn)及取心資料分析法

利用不同含水階段油井密閉取心井、巖心水驅(qū)油實(shí)驗(yàn)等資料,對(duì)儲(chǔ)層物性參數(shù)、孔隙結(jié)構(gòu)參數(shù)及儲(chǔ)層滲流特征變化規(guī)律等進(jìn)行分析研究是目前最常規(guī)的研究方法之一。其中儲(chǔ)層微觀物性參數(shù)包括孔喉半徑(Rmax、Ravg、Rmain、R50)、孔喉比、孔喉形狀及配位數(shù)、分選系數(shù)Sp、變異系數(shù)Skp、峰態(tài)Kp和歪度等[8-9]。

大慶油田、勝利油田經(jīng)過(guò)長(zhǎng)期注水開(kāi)發(fā),積累了大量礦場(chǎng)資料,多位學(xué)者通過(guò)各開(kāi)發(fā)區(qū)塊不同開(kāi)發(fā)階段的密閉取心井資料,綜合利用掃描電鏡、鑄體薄片、核磁共振、驅(qū)油實(shí)驗(yàn)和生產(chǎn)動(dòng)態(tài)、壓汞實(shí)驗(yàn)等方法對(duì)孔隙結(jié)構(gòu)參數(shù)、儲(chǔ)層物性以及巖性參數(shù)的變化進(jìn)行分析,儲(chǔ)層微觀參數(shù)變化特質(zhì)具備較高的一致性[8-14]。總體上,長(zhǎng)期注水沖刷主要影響巖石骨架和孔隙結(jié)構(gòu),不同油藏的物性變化規(guī)律及變化幅度有一定差異,但在一定范疇內(nèi),其變化趨勢(shì)具有一致性。對(duì)于高滲巖樣(氣測(cè)滲透率Ka=2 300 mD),沖刷后巖樣的孔隙度、粒度中值等參數(shù)均有增加趨勢(shì)(圖1),分選系數(shù)、泥質(zhì)含量、粉砂含量等明顯減少[10],平均孔喉半徑、孔喉半徑中值增加,中大孔喉個(gè)數(shù)增加,直觀上影響了滲透率,滲透率貢獻(xiàn)率也隨之增加,低滲透儲(chǔ)層物性則趨于變差[13]。

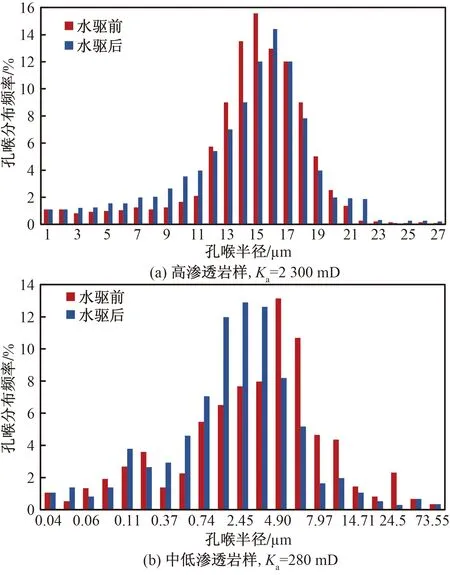
圖1 不同滲透率儲(chǔ)層水驅(qū)前后孔喉半徑變化[13]Fig.1 Changes in pore throat radius of the reservoirs with different permeability before and after water flooding[13]

1.2 三維孔隙網(wǎng)絡(luò)模擬模型

傳統(tǒng)的滲流研究多為宏觀研究,如對(duì)孔隙度、滲透率、潤(rùn)濕性等展開(kāi)分析,其不足之處是不能確定多孔介質(zhì)內(nèi)部的物理、化學(xué)變化特征。Fatt[15]在1956年最先提出網(wǎng)絡(luò)模型概念,后被廣泛用于描述和研究?jī)?chǔ)層的微觀孔隙結(jié)構(gòu)與滲流特性[16-27]。

孔隙網(wǎng)絡(luò)模型是將多孔介質(zhì)中復(fù)雜的孔隙結(jié)構(gòu)抽象為理想的幾何形狀,可進(jìn)一步分為隨機(jī)網(wǎng)絡(luò)模型和真實(shí)巖心的網(wǎng)絡(luò)模型[17]。構(gòu)建隨機(jī)網(wǎng)絡(luò)模型只需按巖心孔喉數(shù)據(jù)在規(guī)則的網(wǎng)格中隨機(jī)分布孔隙和喉道,而不需要借助任何實(shí)驗(yàn)數(shù)據(jù),其在研究?jī)?chǔ)層參數(shù)變化的內(nèi)在機(jī)理時(shí)優(yōu)勢(shì)明顯[18]。李振泉等[19]建立了油水兩相流三維網(wǎng)絡(luò)模擬模型,討論了不同儲(chǔ)層潤(rùn)濕性下孔喉結(jié)構(gòu)參數(shù)對(duì)剩余油分布規(guī)律的影響,并給出模擬驅(qū)替過(guò)程中含水飽和度、絕對(duì)滲透率和相對(duì)滲透率等計(jì)算方法。徐暉等[20]建立了考慮微粒運(yùn)移的三維網(wǎng)絡(luò)模擬模型,利用有限差分求解方法,量化分析了長(zhǎng)期水驅(qū)砂巖油藏孔喉結(jié)構(gòu)變化規(guī)律,并與實(shí)驗(yàn)結(jié)果進(jìn)行對(duì)比,驗(yàn)證模型的可靠性。馮其紅等[21]、肖康等[22]通過(guò)考慮孔喉內(nèi)微粒的脫落、運(yùn)移、堵塞及由優(yōu)勢(shì)通道引起的附加壓力損耗,建立了動(dòng)態(tài)的三維網(wǎng)絡(luò)模型,從機(jī)理上研究了影響優(yōu)勢(shì)通道發(fā)育的主要孔喉結(jié)構(gòu)參數(shù),并模擬得到不同膠結(jié)程度、注采強(qiáng)度下孔隙度、滲透率的變化規(guī)律。

隨機(jī)網(wǎng)絡(luò)模型中的孔喉參數(shù)是通過(guò)分布函數(shù)隨機(jī)賦值,難以開(kāi)展實(shí)際應(yīng)用[17]。而基于真實(shí)巖心的網(wǎng)絡(luò)模型則能最大限度地模擬實(shí)際巖心的孔喉大小和空間分布,由于構(gòu)建過(guò)程需要借助實(shí)驗(yàn),成本較為昂貴,國(guó)內(nèi)受設(shè)備和技術(shù)條件所限,研究薄弱,因此在進(jìn)一步用于解剖水驅(qū)油藏儲(chǔ)層微觀物性參數(shù)變化規(guī)律方面研究也相應(yīng)較少[23]。但經(jīng)過(guò)多年探索,重構(gòu)數(shù)字巖心及構(gòu)建孔隙網(wǎng)絡(luò)模型的技術(shù)和算法得到快速發(fā)展[24-27],未來(lái)關(guān)于數(shù)字巖心構(gòu)建的孔隙網(wǎng)絡(luò)模型勢(shì)必會(huì)成為儲(chǔ)層孔隙結(jié)構(gòu)及其變化規(guī)律研究的有力工具。

1.3 孔隙結(jié)構(gòu)分形表征

法國(guó)數(shù)學(xué)家Mandelbrot等[28]提出并創(chuàng)立了分形幾何理論,認(rèn)為孔隙大小指數(shù)分布與分形維數(shù)存在一種冪律關(guān)系,Katz等[29]通過(guò)大量數(shù)據(jù)分析發(fā)現(xiàn)砂巖孔隙空間以及孔隙表面都具有很好的分形特性,在一定孔隙半徑范圍內(nèi)可以用分形維數(shù)來(lái)表征儲(chǔ)層孔隙結(jié)構(gòu)特征。研究表明,砂巖孔隙結(jié)構(gòu)的分形維數(shù)介于2～3,分形維數(shù)越大,儲(chǔ)層孔隙結(jié)構(gòu)越復(fù)雜,非均質(zhì)性越強(qiáng)[30]。國(guó)內(nèi)外學(xué)者先后提出了利用分形維數(shù)描述孔隙結(jié)構(gòu)的復(fù)雜程度和變化規(guī)律,并建立了孔隙結(jié)構(gòu)特征參數(shù)的分形表征模型[31-33]。

利用分形理論研究非常規(guī)儲(chǔ)層巖性特征是近幾年研究的熱點(diǎn)[34-35],但用于定量表征長(zhǎng)期水驅(qū)砂巖儲(chǔ)層孔隙結(jié)構(gòu)非均質(zhì)性的變化規(guī)律較少。王天琦等[36]綜合利用巖樣壓汞資料和測(cè)井資料獲取Df(孔隙結(jié)構(gòu)分形維數(shù))、孔隙度、滲透率等物性參數(shù),利用聚類分析回歸Df預(yù)測(cè)模型,該方法簡(jiǎn)單,但測(cè)井解釋的孔隙度、滲透率精度有限。文華[23]利用大慶喇薩杏油田巖心驅(qū)替實(shí)驗(yàn)和壓汞實(shí)驗(yàn)資料,回歸了水驅(qū)前后滲透率、最大孔喉半徑和孔喉半徑中值與分形維數(shù)的關(guān)系曲線(圖2),并計(jì)算不同含水率下的孔喉分形維數(shù),建立了儲(chǔ)層孔隙結(jié)構(gòu)分形維數(shù)動(dòng)態(tài)演化的數(shù)學(xué)模型。掃描圖像也可直觀反映孔隙結(jié)構(gòu),目前利用掃描圖像分析孔隙結(jié)構(gòu)分形維數(shù)的研究尚處于起步階段,但也是孔隙結(jié)構(gòu)參數(shù)定量化表征的方向之一。

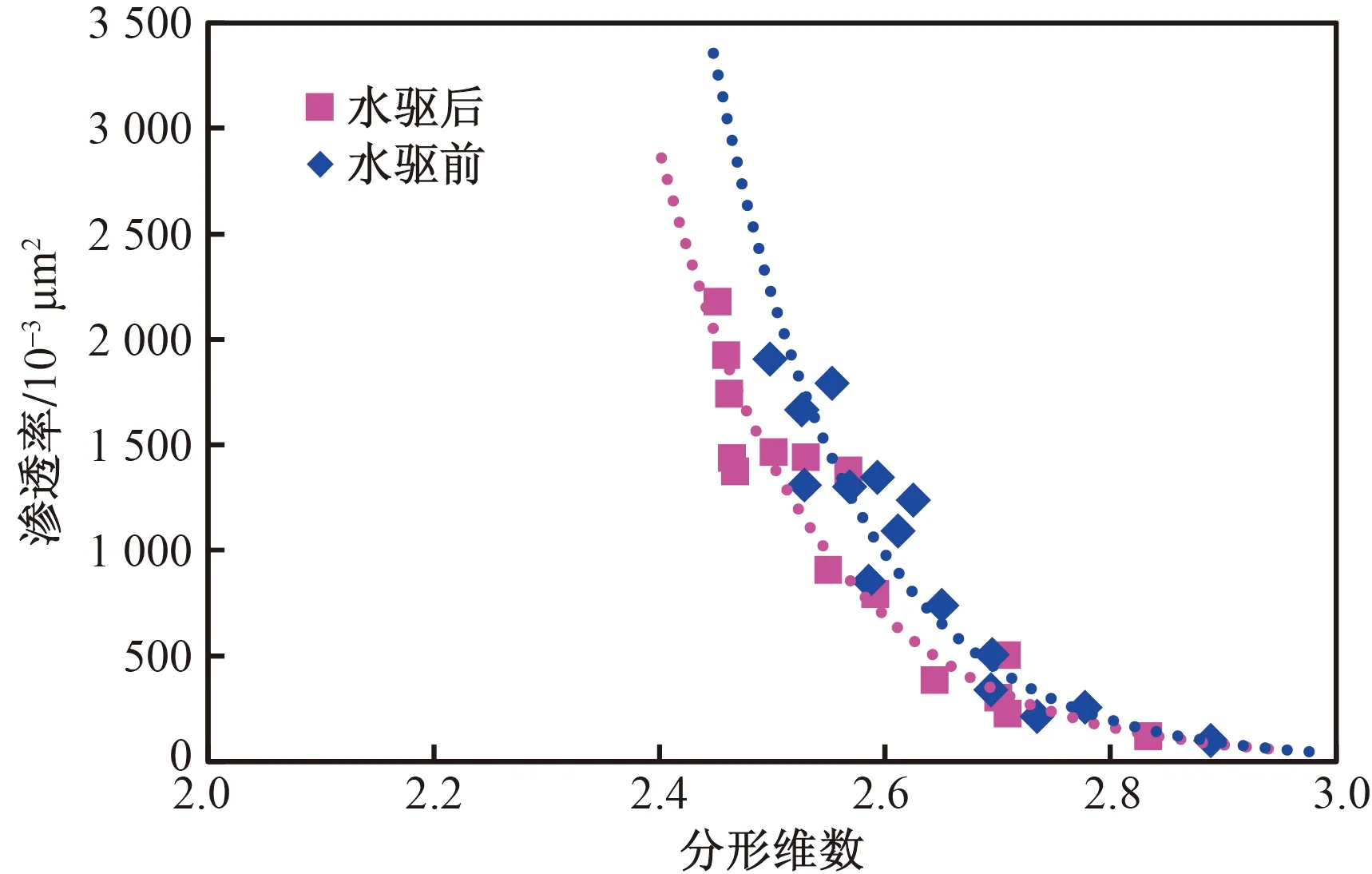
圖2 分形維數(shù)與滲透率關(guān)系曲線[23]Fig.2 Relationship curve between fractal dimension and permeability[23]

2 儲(chǔ)層宏觀物性時(shí)變規(guī)律研究現(xiàn)狀

2.1 滲透率時(shí)變分析

儲(chǔ)層宏觀參數(shù)變化定量分析需要解決兩個(gè)問(wèn)題,一是儲(chǔ)層宏觀參數(shù)如何變化,二是確定時(shí)變表征參數(shù)。油藏?cái)?shù)值模擬不直接采用微觀參數(shù),而是通過(guò)宏觀參數(shù)(滲透率、孔隙度、相滲曲線等)反映儲(chǔ)層物性時(shí)變現(xiàn)象[37]。這一方面國(guó)內(nèi)研究較多,不同開(kāi)發(fā)階段孔滲數(shù)據(jù)獲取方法主要包括:密閉取心資料分析、巖心水驅(qū)油實(shí)驗(yàn)、測(cè)井儲(chǔ)層評(píng)價(jià)、試井資料解釋。密閉取心資料可以直接獲得水洗后儲(chǔ)層物性數(shù)據(jù);巖心驅(qū)替實(shí)驗(yàn)與壓汞實(shí)驗(yàn)交替進(jìn)行的分析方法,可研究巖樣在不同沖刷倍數(shù)下宏觀物性參數(shù)的變化規(guī)律;測(cè)井儲(chǔ)層評(píng)價(jià)法可分析不同階段完鉆井的孔隙度、滲透率、泥質(zhì)含量等變化特點(diǎn),研究相應(yīng)物性參數(shù)隨水驅(qū)開(kāi)發(fā)過(guò)程的演化模式[38]。

大量實(shí)驗(yàn)和礦場(chǎng)資料顯示,水驅(qū)開(kāi)發(fā)過(guò)程中,孔隙度變化不大,一般都在測(cè)量誤差范圍之內(nèi)[1],滲透率則因儲(chǔ)集層物性差異而具有各自不同的變化規(guī)律[13](圖3)。

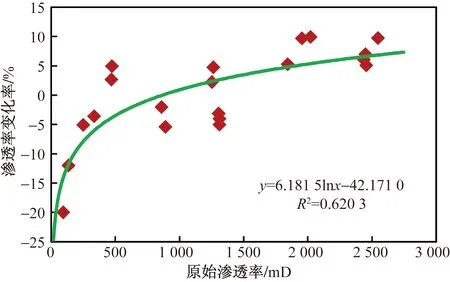
圖3 巖心水驅(qū)后滲透率變化率與原始滲透率的關(guān)系[13]Fig.3 Relationship between the change rate of permeability and original permeability of water flooded cores[13]

儲(chǔ)層物性時(shí)變的表征方法可劃分為單因素法、多因素法、水驅(qū)強(qiáng)度表征法,其中水驅(qū)強(qiáng)度表征法能體現(xiàn)注水沖刷作用,更為客觀,且易應(yīng)用于數(shù)值模擬中[37]。在物性時(shí)變表征的研究中,早期根據(jù)勝利油區(qū)利用礦場(chǎng)密閉取心井資料統(tǒng)計(jì)回歸得到滲透率變化倍數(shù)與含水率的關(guān)系[39],但并未體現(xiàn)滲透率變化的根本原因;利用過(guò)水倍數(shù),即累積注入量與孔隙體積之比,作為表征參數(shù),體現(xiàn)了注水沖刷對(duì)各宏觀參數(shù)的影響,可實(shí)現(xiàn)連續(xù)性和方向性表征[40-48]。但計(jì)算出的過(guò)水倍數(shù)受網(wǎng)格大小影響大,姜瑞忠等[42]、魏峰[45]、趙平起等[46]分別提出面通量、累計(jì)面通量、有效驅(qū)替通量等概念,其中面通量可以解決網(wǎng)格大小問(wèn)題,有效驅(qū)替通量在面通量的基礎(chǔ)上考慮孔隙度,可以準(zhǔn)確描述注入水的真實(shí)流速,流速越大,作用在巖石顆粒上的壓力梯度越大,巖石顆粒越容易脫落并運(yùn)移,孔喉變化越顯著。金忠康等[47]則是將上述過(guò)水倍數(shù)轉(zhuǎn)換為含水飽和度變化量,并利用商業(yè)軟件實(shí)現(xiàn)滲透率時(shí)變數(shù)值模擬。

總體看,目前物性時(shí)變主要根據(jù)室內(nèi)水驅(qū)油實(shí)驗(yàn)和密閉取心井資料進(jìn)行分析(表1),但大部分油田巖樣分析數(shù)據(jù)有限,參數(shù)點(diǎn)可能存在較大波動(dòng),不足以形成可靠規(guī)律;利用分形理論進(jìn)行儲(chǔ)層物性變化定量描述,也需要基于不同水驅(qū)階段巖心壓汞實(shí)驗(yàn)數(shù)據(jù);測(cè)井評(píng)價(jià)法中不同階段鉆完井測(cè)井解釋滲透率也基于初始孔滲關(guān)系,其數(shù)據(jù)精度可靠性有限。綜上,目前對(duì)滲透率定量時(shí)變參數(shù)表征精確度不夠,能直觀反映滲透率變化參數(shù)數(shù)據(jù)點(diǎn)不足。

表1 調(diào)研油田滲透率時(shí)變規(guī)律總結(jié)Table 1 Variation laws of permeability in water-flooding reservoir

2.2 相滲曲線時(shí)變分析現(xiàn)狀

國(guó)內(nèi)外大量研究表明,經(jīng)過(guò)長(zhǎng)時(shí)間注水開(kāi)發(fā),儲(chǔ)層巖石表面吸附原油能力降低,巖石潤(rùn)濕性向親水方向增強(qiáng),殘余油飽和度降低,等滲點(diǎn)右移,兩相流動(dòng)區(qū)間增大[1,49-51]。為實(shí)現(xiàn)相滲曲線定量、連續(xù)時(shí)變表征,需要獲取隨開(kāi)發(fā)過(guò)程不斷變化的相滲曲線。由于直接測(cè)定相滲曲線昂貴耗時(shí),且難以代表整個(gè)油藏,前人在間接獲取相滲曲線方法上研究頗多,總結(jié)為如下3類方法。

(1)礦場(chǎng)資料回歸統(tǒng)計(jì)。劉顯太[40]對(duì)勝利油區(qū)中高滲透砂巖油藏相對(duì)滲透率曲線進(jìn)行統(tǒng)計(jì)分析,回歸得到了端點(diǎn)變化值與滲透率變化倍數(shù)以及油、水相滲透率與絕對(duì)滲透率的關(guān)系。王守磊等[52]、呂棟梁等[53]通過(guò)交替條件期望法對(duì)多個(gè)影響相滲曲線的儲(chǔ)層物性參數(shù)進(jìn)行多元回歸,根據(jù)相滲曲線冪函數(shù)式,建立了相滲曲線4個(gè)端點(diǎn)以及特征參數(shù)表征模型。

(1)

(2)

式中:Krw為水相相對(duì)滲透率;Kro為油相相對(duì)滲透率;Krw(Sor)為殘余油飽和度下的水相相對(duì)滲透率;Kro(Swi)為束縛水飽和度下的油相相對(duì)滲透率;Sw為含水飽和度;Swi為初始含水飽和度;Sor為殘余油飽和度;m為水相指數(shù);n為油相指數(shù)。

(2)動(dòng)態(tài)資料反演。油田開(kāi)發(fā)到中后期,多位學(xué)者提出利用動(dòng)態(tài)數(shù)據(jù)計(jì)算相滲曲線,根據(jù)不同水驅(qū)曲線適應(yīng)條件的差異,分別利用甲、乙、丙、丁、俞啟泰、張金慶水驅(qū)特征曲線及新型近似理論水驅(qū)曲線,結(jié)合相滲曲線經(jīng)驗(yàn)公式,推導(dǎo)出油水相指數(shù)、殘余油飽和度的數(shù)學(xué)表達(dá)式,并計(jì)算相滲曲線[54-57]。

(3)機(jī)器學(xué)習(xí)算法仿真預(yù)測(cè)。李春雷等[58]提出機(jī)器學(xué)習(xí)算法獲取實(shí)時(shí)、準(zhǔn)確的相滲曲線,充分利用現(xiàn)場(chǎng)測(cè)井曲線資料,優(yōu)選敏感參數(shù),結(jié)合相滲曲線特征點(diǎn)數(shù)據(jù),構(gòu)建水驅(qū)儲(chǔ)層相滲曲線預(yù)測(cè)樣本集,優(yōu)選機(jī)器學(xué)習(xí)算法對(duì)油水相相對(duì)滲透率進(jìn)行預(yù)測(cè),并從地質(zhì)因素和端點(diǎn)值進(jìn)行約束優(yōu)化,實(shí)現(xiàn)高精度相滲曲線的智能生成。

在如何連續(xù)表征相滲曲線的動(dòng)態(tài)變化問(wèn)題上,目前主要是將相滲曲線的時(shí)變問(wèn)題轉(zhuǎn)換為相滲曲線端點(diǎn)及油水相指數(shù)的時(shí)變[41]。礦場(chǎng)資料回歸統(tǒng)計(jì)及機(jī)器學(xué)習(xí)算法預(yù)測(cè)兩種方法均基于不同儲(chǔ)層物性參數(shù)獲取相滲曲線,具有多解性,且難以直接應(yīng)用到數(shù)值模擬中,動(dòng)態(tài)資料反演法計(jì)算的是某一開(kāi)發(fā)階段的相滲曲線,未能實(shí)現(xiàn)相滲曲線變化的連續(xù)表征。

2.3 數(shù)值模擬軟件模擬物性時(shí)變發(fā)展現(xiàn)狀

國(guó)內(nèi)外主流數(shù)值模擬軟件主要包括斯倫貝謝Petrel RE平臺(tái)、CMG軟件以及tNavigator。2017年斯倫貝謝Petrel RE平臺(tái)及Intersect模擬器可利用Python語(yǔ)言實(shí)現(xiàn)儲(chǔ)層物性變化的分區(qū)動(dòng)態(tài)表征[59]。CMG軟件從影響微粒運(yùn)移的因素、數(shù)值模型中微粒的類型、與微粒運(yùn)移和溫度有關(guān)的潤(rùn)濕性變化等幾方面模擬微粒運(yùn)移。tNavigator軟件利用過(guò)水倍數(shù),表征流體對(duì)儲(chǔ)層的沖刷程度,對(duì)可變參數(shù)滲透率、傳導(dǎo)率、相滲曲線進(jìn)行時(shí)變模擬,并允許設(shè)置時(shí)變參數(shù)上限值,防止其溢出理論范圍。

2.4 儲(chǔ)層物性時(shí)變研究技術(shù)展望

傳統(tǒng)巖心分析、室內(nèi)驅(qū)替實(shí)驗(yàn)等方法在應(yīng)用過(guò)程中存在手段單一、局限性大等問(wèn)題,而基于實(shí)際巖心或數(shù)字巖心的孔隙網(wǎng)絡(luò)模型、孔隙分形表征等技術(shù)具有可重復(fù)性及預(yù)測(cè)性,在非常規(guī)油氣儲(chǔ)層孔隙結(jié)構(gòu)描述中廣泛研究與應(yīng)用[34,60-61],其也是研究水驅(qū)砂巖油藏儲(chǔ)層物性時(shí)變行之有效的方法。此外,儲(chǔ)層物性時(shí)變影響因素眾多,現(xiàn)場(chǎng)應(yīng)用多基于具體油田巖心分析結(jié)果進(jìn)行統(tǒng)計(jì)回歸,且僅考慮了部分因素,難以有效推廣。近年來(lái)大數(shù)據(jù)、機(jī)器學(xué)習(xí)算法等在油氣行業(yè)快速發(fā)展,為綜合考慮開(kāi)發(fā)、地質(zhì)等多因素影響下的儲(chǔ)層物性參數(shù)變化預(yù)測(cè)提供了新手段。

在儲(chǔ)層物性時(shí)變理論應(yīng)用到實(shí)際油田開(kāi)發(fā)過(guò)程中,商業(yè)數(shù)值模擬軟件的逐步完善,使得通過(guò)建立油藏動(dòng)態(tài)地質(zhì)模型精細(xì)模擬和預(yù)測(cè)優(yōu)勢(shì)通道及剩余油分布易于實(shí)現(xiàn),從而為油田開(kāi)發(fā)調(diào)整、分采分注、優(yōu)化措施等提供更加可靠的依據(jù)。同時(shí),儲(chǔ)層物性時(shí)變理論在水驅(qū)砂巖油藏中實(shí)現(xiàn)應(yīng)用,又將進(jìn)一步深入推動(dòng)其他各類油藏儲(chǔ)層物性的時(shí)變研究。

3 結(jié)論

(1)掃描電鏡、鑄體薄片、核磁共振、密閉取心井分析、壓汞實(shí)驗(yàn)、驅(qū)油實(shí)驗(yàn)是研究長(zhǎng)期注水沖刷對(duì)儲(chǔ)層物性參數(shù)影響的主要手段,該類方法可分析黏土礦物的分布、巖石骨架、孔隙結(jié)構(gòu)等微觀參數(shù)的變化,進(jìn)而分析宏觀物性參數(shù)孔隙度、滲透率的變化。

(2)基于真實(shí)巖心構(gòu)建的孔隙網(wǎng)絡(luò)模型可最大限度地模擬實(shí)際目標(biāo)巖心的孔喉大小和空間分布,具有可重復(fù)性、可控制性的特點(diǎn),而在描述儲(chǔ)層微觀孔隙結(jié)構(gòu)中引入分形幾何理論,將宏觀與微觀結(jié)合實(shí)現(xiàn)物性時(shí)變的定量表征。兩種方法目前尚處于發(fā)展階段,也是未來(lái)研究?jī)?chǔ)層微觀孔隙結(jié)構(gòu)的重要發(fā)展方向。

(3)密閉取心資料分析、巖心水驅(qū)實(shí)驗(yàn)是獲取儲(chǔ)層宏觀參數(shù)定量時(shí)變規(guī)律最直接且主要手段,但其只能代表油藏局部物性變化,巖心數(shù)量有限時(shí),能直觀反映滲透率變化的數(shù)據(jù)點(diǎn)不足。

(4)相滲曲線形態(tài)隨注水沖刷發(fā)生明顯變化,其定量、連續(xù)時(shí)變表征可通過(guò)相滲曲線特征參數(shù)的連續(xù)時(shí)變實(shí)現(xiàn),但仍受經(jīng)驗(yàn)公式及回歸擬合精度的影響。