穩態隨機激勵下結構阻尼系統的拓撲優化方法

劉偉佳，趙旭奇

結構拓撲優化是在設計領域內找到形狀配置和材料分布的設計方法.各類拓撲優化方法已廣泛應用于靜載荷下的結構設計和實際工程問題［1-2］.在工程應用中，結構設計問題經常會遇到隨機因素，如隨機參數和材料特性、邊界條件和外部載荷的不確定性［3-6］.其中一個關鍵課題是在穩態隨機激勵下的結構設計［7］.因此，本文介紹了一種基于虛擬激勵法（PEM）［8］的大規模結構在穩態隨機激勵下的拓撲優化方法.該優化模型以寬頻率區間內隨機位移的功率譜密度（PSD）為目標函數.此外，還考慮了一類具有結構阻尼的線性動力系統及其在穩態隨機激勵下的結構響應.該方法結合頻率響應計算［9］及隨機響應的PEM 方法，以計算寬頻率區間內的頻域解.優化模型中目標函數的導數基于伴隨方法得到，其中伴隨向量同樣可用本文方法求解.數值實驗驗證了本方法的高效性.

1 計算方法

外激勵作用下，結構阻尼系統經有限元方法離散后的運動控制方程可以寫成如下形式：

其中：M為系統的質量矩陣；為相應的剛度矩陣；η為材料的阻尼系數；(t)，X(t)為系統加速度及位移向量；B為n×d維隨機激勵定位向量；f(t)為d維穩態隨機激勵向量，其功率譜（SPD）矩陣為Sf.

基于PEM［8］，輸入與輸出的SPD 矩陣及有如下關系：

其中：為H的共軛矩陣，H(ω)為復頻率響應矩陣，且滿足

因此，輸入激勵f(t)的SPD 矩陣Sf為非負定Hermite 矩陣且可分解為根據輸入與輸出SPD 矩陣之間的關系，可以得到：

由此，可利用PEM 將穩態隨機激勵分析轉化為如下結構頻率響應分析：

在每個代求頻率點，對系數矩陣進行分解回代可得到響應的精確解.然而，對于大規模系統如此會產生巨大的計算量.模態疊加法通過將相應無阻尼系統的特征向量線性疊加得到結構響應，其精度隨著模態數量的增加而提高.對于大規模結構無法求得所有特征向量，因此通過截斷的方法構造如下虛擬頻率響應向量u(ω)的形式：

其中：ΦL為已求得的無阻尼系統特征向量；ΦH為截斷的無阻尼系統特征向量.結構響應的截斷部分極大影響虛擬頻率響應向量u(ω)的精度.

本文主要討論引入方法高效計算截斷部分w(ω)的近似解.考慮到結構模態關于矩陣M正交性關系，w(ω)滿足如下形式：

下面將利用迭代的方法計算w(ω)，其表達形式可近似寫成

其中：向量pi由如下迭代格式得到

并得到相應的系數a0及系數向量z(ω)，由于迭代格式的收斂性由譜半徑決定.具體推導過程可參考文獻［9］.

基于密度法的穩態隨機激勵下結構拓撲優化模型［10］可有：

其中：ρe為設計變量，其意義為單元e的密度；為了確保迭代過程中質量與剛度矩陣不出現奇異設置ρmin= 0.001；ve為單元e的體積，V0為設計區域的總體積，優化模型中的目標函數為考慮頻段內某一自由度r的功率譜密度積分，且

在動力學拓撲優化過程中，由于設計變量的更新造成剛度與質量不匹配，導致系統出現局部模態的現象.基于這樣的數值不穩定性，已有許多改善方案，在一定程度上解決了局部模態的現象.本文采用的是多項式插值方案［11］.

靈敏度分析假定外部激勵與設計變量無關.本文選擇伴隨方法計算目標函數的靈敏度.對于設計變量數量較大的情況，該方法是優選的.它還可以避免計算特征向量導數，因為這在直接微分法中是一項困難的任務.具體推導過程可參考文獻［12］.此外，基于密度方法的結構拓撲優化可能會遇到數值不穩定現象，如棋盤格和網格依賴性.網格過濾技術可以用來避免這些問題.最后，利用GCMMA算法作為優化問題的求解方法［13］.

2 數值實驗

如圖1 所示，考慮設計區域為1 m×0.5 m，厚度0.01 m 的矩形，結構左側固定.利用有限元方法將該區域劃分為200×100 個平面4 節點應力單元，系統包含40 400 自由度.體積約束為小于30%.結構左側中點處沿y軸方向施加白噪聲激勵，其功率譜密度大小為104m2/Hz.楊氏模量E= 7 × 1010Pa，泊松比υ= 0.35，密度ρ= 2 700 kg/m3，結構阻尼系數η= 0.01.優化過程的收斂準則為相鄰迭代步的目標函數相對誤差小于10-4.目標函數為［0，300］Hz，［0，600］Hz 和［0，1 000］Hz 內荷載加載自由度PSD 值的積分.為了保證結構響應的計算效率，將迭代格式中的收斂準則設為10-6.

圖1 二維懸臂梁

優化模型的初值選擇是將所有的設計變量ρe均設置為0.3，相應結構的基頻為93 Hz.基于本文所提出方法的總耗時及相應頻段的初始、收斂的優化目標函數值見表1.

基于本文的拓撲優化方法，三個不同頻段穩態隨機激勵下的優化結果如圖2 所示.

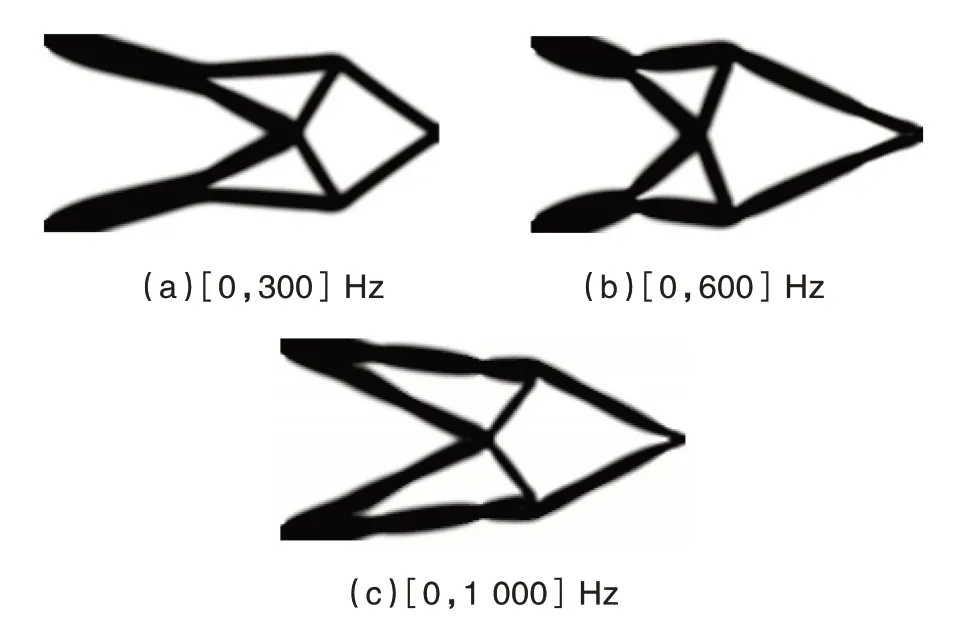
圖2 各頻段激勵下的最優化設計

圖2（a）~圖2（c）中的優化結構的基頻，分別為202.9 Hz、275.5 Hz、341.0 Hz.為了比較三個優化構型在各自考慮區間內的動力學性能，其荷載自由度在頻段［0，1 000］Hz 的功率譜密度如圖3 所示.可以發現，隨著激勵頻段的擴大，優化結構的基頻會隨之增大，且動力學響應會極大地影響最終的優化構型.表2 列出了在各自頻段激勵下利用本文方法計算初始結構響應的CPU 時間具體分布.為了較好地評估本方法的精確性，計算結構響應的相對誤差

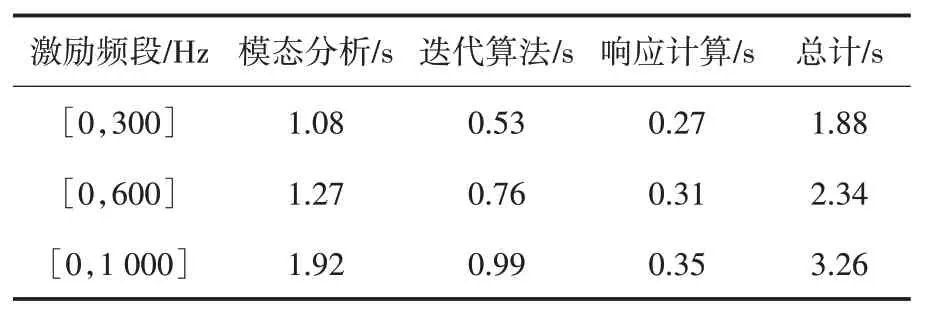
表2 初始結構計算響應的CPU 時間分布

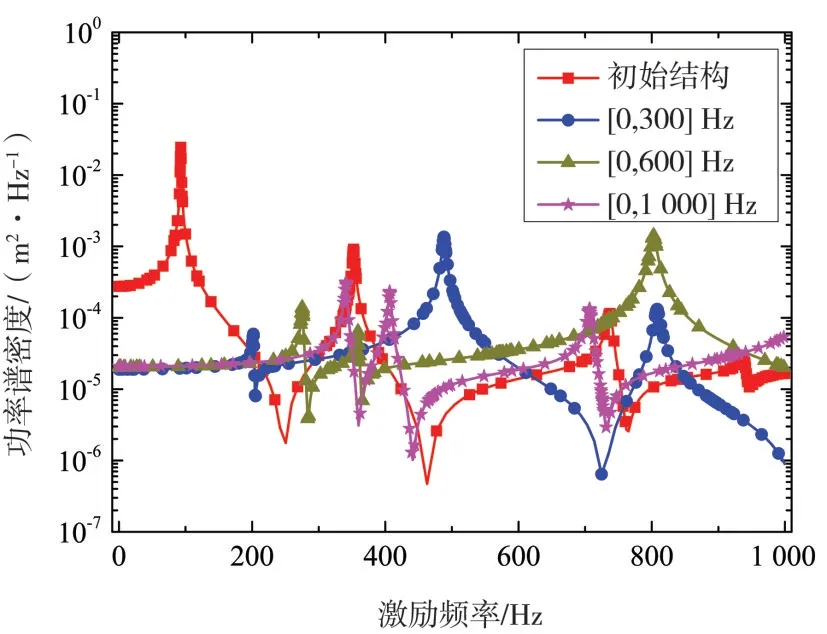
圖3 初始結構與最優化設計的功率譜密度響應曲線

其誤差曲線如圖4 所示.由文獻［9］中的推導可知，迭代格式的譜半徑在頻率區間的最右端ωR達到最大值.因此，截斷模態部分中的向量pi可有最高激勵頻率自適應地確定，結構響應的表達式在整個頻率間隔內都是有效的.這部分理論很好地驗證了圖4 的結果，初始結構響應向量的相對誤差值在ωR達到最大且小于10-8.

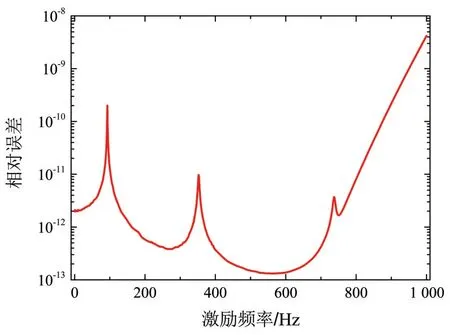
圖4 基于本文方法的初始結構頻率響應相對誤差曲線

3 結語

本文提出了結構阻尼系統隨機響應拓撲優化方法.與傳統的拓撲優化方法相比，該方法具有更高的精度和適應性，主要體現在三個方面.第一，方法可以根據用戶定義的迭代算法的收斂速度自適應地確定模態疊加中涉及的低階模態.第二，可基于給定的容差誤差計算結構響應.最后，能夠在更新設計變量后自適應調整計算過程.迭代算法只需要很短的CPU 處理時間，并且只占用小部分存儲空間，即使對于大規模的結構問題也同樣有效.通過伴隨方法，本方法也可以對目標函數進行靈敏度分析.數值實驗驗證了該方法的準確性和有效性.對于給定自由度下隨機位移的PSD 最小化問題，基于本方法的拓撲優化過程，不僅提高了計算精度，而且顯著減少了CPU 時間.