基于流管法的水平井組開發指標預測模型及應用

李文忠，江遠鵬，段 宇，常會江，吳曉慧

（中海石油（中國）有限公司天津分公司，天津 300452）

油藏動態分析是油氣田開發的重要工作，經典的動態分析方法主要有童氏圖版法、水驅特征曲線法、油藏數值模擬等方法[1-3]。通過對比實際生產資料與理論計算結果的關系，判斷油田開發生產形勢和確定最終采收率。但是經典方法側重油田整體研究，對井組級別的研究不夠靈活。

流管法具有模型相對簡單，計算速度快，參數調整靈活等特點。它豐富了油藏數值模擬的思路和方法，提供了形象、快速解決油田開發問題的途徑[4]。MUSKAT等[5]于1934 年首次提出流管法的概念，但最早的模擬研究模型較簡單，主要是針對均質地層、單相流體的滲流模擬。1962 年HIGGINS 等[6]選擇采用實驗方法獲得流管的油水兩相分布，Buckley-Leverett 等則從理論上推導了一維兩相水驅油規律。從物模和數模兩方面將流管法發展至兩相。隨后Martin、Batycky、Kulkani 等多名學者和軟件公司將流管法推廣至三維空間，并用來模擬化學驅等采油技術。但這些方法大都是基于軟件平臺和數值方法。計算過程相對比較復雜，而且不夠透明和靈活。

考慮到各方法的特點和不足，本文提出了基于流管法的水平井組開發指標預測模型。該模型基于水平井組流線分布的規律，通過流管滲透率、流管體積和流管長度描述了井間非均質性、井控儲量、井距等關鍵參數。基于Buckley-Leverett 水驅油理論，對模型進行了求解，將動態研究推進至井組級別[7－9]。

1 數學模型

1.1 模型假設

假設水平井具有無限導流能力，根據水平井勢函數和流函數，繪制水平井間的壓力和流線分布見圖1、圖2，可以看出水平注采井間大部分流線近似呈直線狀。假設水平井組從注水井到生產井間是由許多流管連接的，不同流管具有不同的滲透率、儲量和長度。如果已知每根流管的注入量，那么根據Buckley-Leverett水驅油理論，則可以計算出這根流管的飽和度分布，進而計算出口端含水飽和度、含水率、產油量、產水量等指標。由于實際井組開發狀況較復雜，為了強化關鍵參數，并簡化模型，對模型作如下假設。

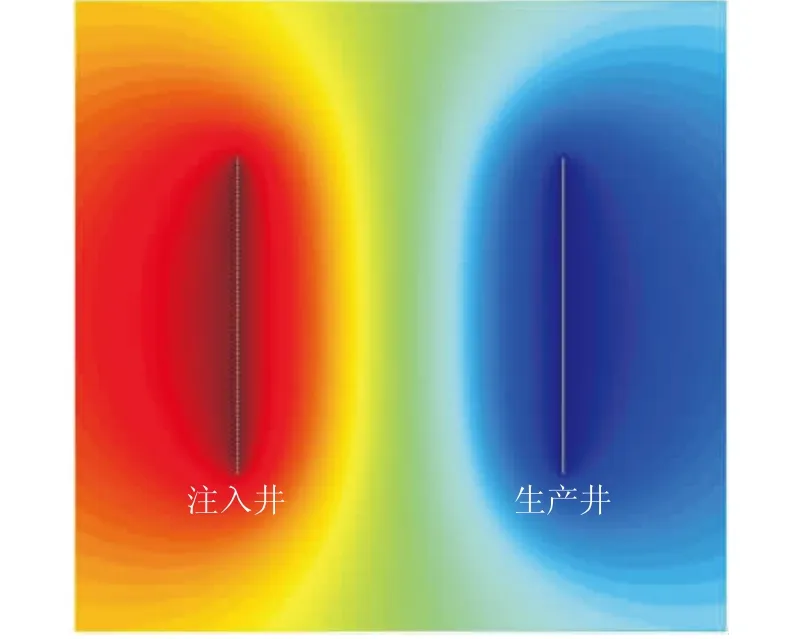
圖1 水平井組勢能分布示意圖

圖2 水平井組等勢面和流線分布示意圖

（1）假設井組開發處于泡點壓力以上，僅有油水兩相流動；

（2）井組保持注采平衡，注入與產出的流體體積相同；

（3）假設水平井段具有無限導流能力，忽略壓力在水平井井筒內的變化；

（4）注采井之間的多根流管彼此之間無竄流。

1.2 單流管求解

根據Buckley-Leverett 水驅油理論，一維兩相水驅油過程中，如果已知注入端的注水量，油、水的黏度，兩相滲透率曲線，便可求出在任意截面的含水率、含水飽和度、水驅前緣的位置及含水飽和度。相關的公式如下：

（1）任意截面的含水率表達式：

式中：fw－含水率，%；Qw－產水量，m3；Q－產液量，m3；Kw－水相滲透率；μw－水的黏度，mPa·s；Ko－油相滲透率；μo－油的黏度，mPa·s；A－流管的橫截面積，m2；P－壓力，MPa。

（2）等飽和度面移動方程：

（3）水驅前緣含水飽和度：

公式（3）是一個含有Swf的隱函數。根據Buckley-Leverett 水驅油理論，Swf可以通過圖解法確定（圖3）。

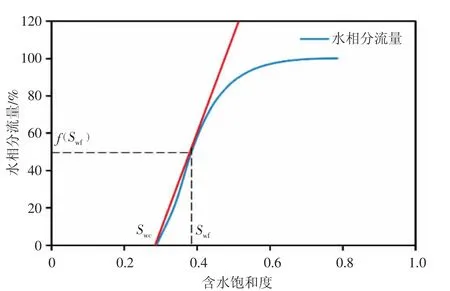
圖3 水驅前緣含水飽和度Swf的確定方法圖

（4）水驅前緣位置的確定：求得水驅前緣含水飽和度Swf以后，再在關系曲線上求出，然后根據公式（2）即可求出水驅前緣所到達的位置。

（5）單流管計算過程及結果：首先，圖解法求取水驅前緣含水飽和度函數，根據油田的相對滲透率數據和黏度數據，繪制fw-Sw曲線。過Swc點，對fw曲線作切線，切點的橫坐標即為Swf。

其次，擬合fw-Sw曲線，保證擬合曲線光滑可導。根據總注入量和等飽和度面移動方程，可以求出任意位置x 處的，進而求出任意位置處的含水飽和度。計算結果見圖4。

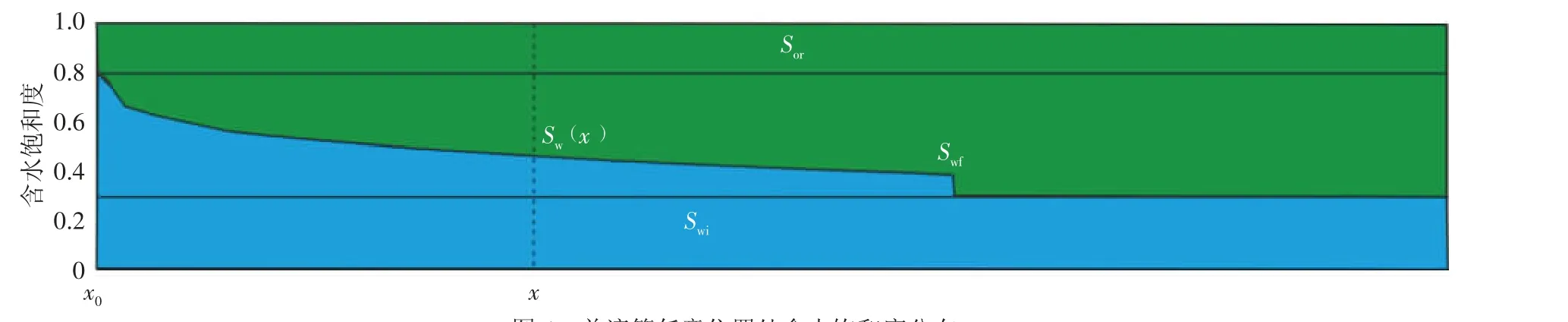
圖4 單流管任意位置處含水飽和度分布

1.3 水平井組轉化為多流管模型的方法

井筒無限導流能力的一注一采水平井組，其井間勢能分布和流線分布見圖1。在井組間流線可以近似認為是許多條長度相等，注入端和出口端壓力分別相同的流管。由于儲層非均質性的影響，不同流管具有不同的滲透率和儲量。為了將實際的井組轉化為流管模型（圖5），需要解決四個問題：

圖5 實際井組轉化為多流管模型示意圖

（1）統計油田的滲透率分布，建立流管模型的對應關系；

（2）將實際油田或井組的儲量劈分到每一根流管上；

（3）計算每個時間節點，每根流管的滲流阻力；

（4）計算每個時間節點，每根流管的吸水量，進而根據Buckley-Leverett 水驅油理論，求取每根流管的含水飽和度分布和產水產油量，匯總后可得到井組的開發指標。

1.3.1 多流管滲透率的確定 根據BZ 油田的滲透率分布特征，結合數理統計理論，綜合分析認為威布爾分布能較為準確地描述油藏滲透率的非均質性[10－11]。

威布爾分布的概率密度函數為：

式中：f 為威布爾分布概率密度函數；δ≥0 為位置參數；α＞1 為形狀參數；β＞1 為尺度參數。威布爾分布的累計概率密度函數為：

根據公式（4）和公式（5），擬合BZ 油田的滲透率分布見圖6、圖7。

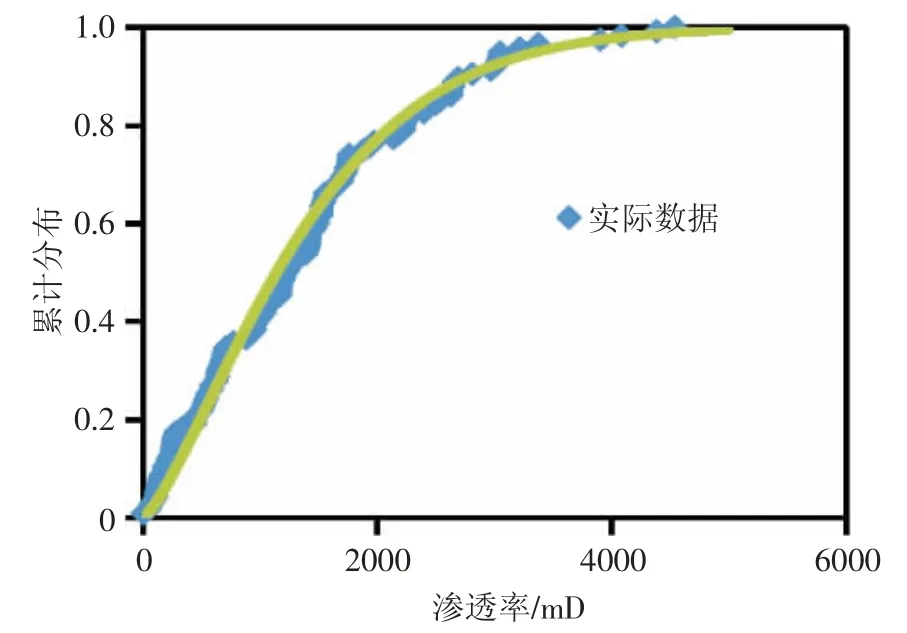
圖6 BZ 油田滲透率累計概率分布擬合

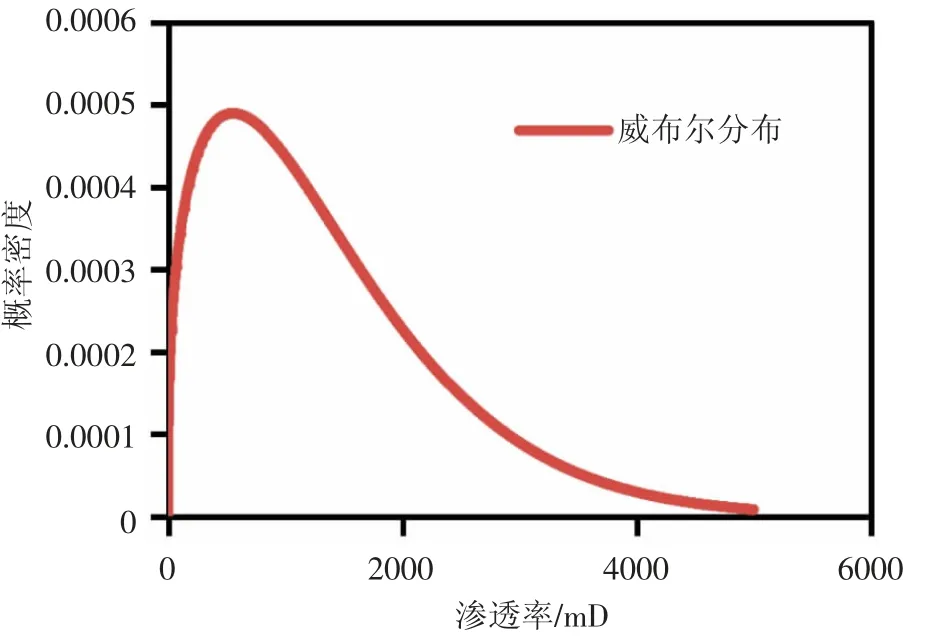
圖7 BZ 油田滲透率概率密度曲線

1.3.2 多流管儲量的劈分 滲透率的分布確定之后，便可確定每根流管對應滲透率的概率密度。但不能僅僅通過滲透率的概率密度進行儲量的劈分。因為滲透率的分布只能決定滲透率空間范圍的參數，要把井控儲量劈分到對應滲透率的流管上，還需要考慮孔隙度的影響。

對于砂巖油藏，孔隙度和滲透率呈現良好的線性關系。統計了BZ 油田孔隙度和滲透率的對應關系，并進行了回歸，見圖8。

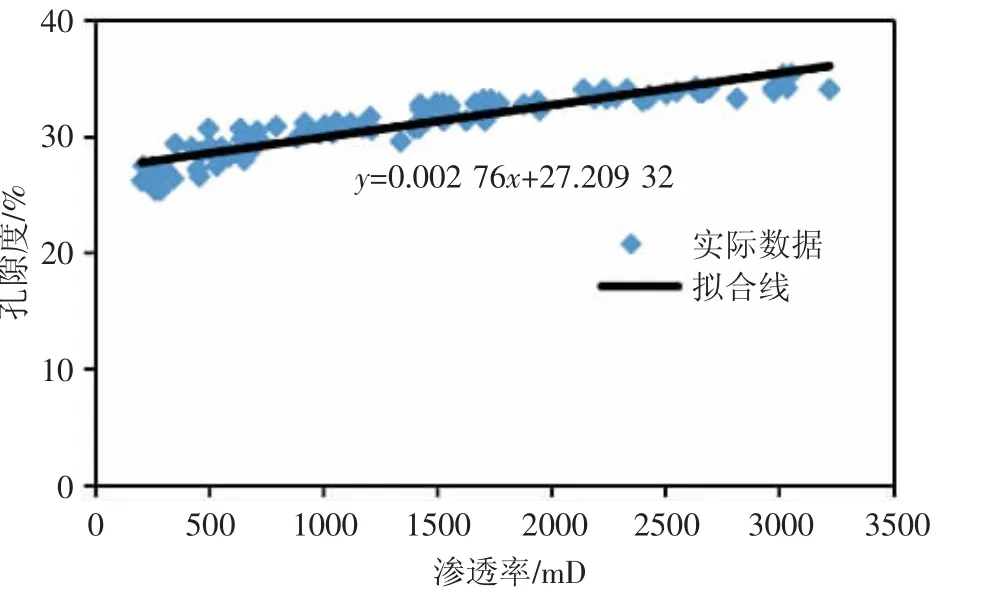
圖8 BZ 油田孔隙度和滲透率關系擬合

對于水平井組，假設多流管長度是相同的，因此，對儲量的劈分等效于求取具有同一滲透率的流管橫截面積。

式中：N-地質含量；L-流管長度；V-總孔隙體積；f（ki）-滲透率為ki的流管對應的累計概率密度；Φ（ki）-滲透率為ki的流管對應的孔隙度。

根據公式（7）即可求出每根流管對應的橫截面積。橫截面積大小與對應滲透率的流管儲量成正比。

1.3.3 單流管的滲流阻力 對于每根流管，井組間壓差可近似認為相同，流管的注入量取決于其滲流阻力。由于在流管不同的位置處，含水飽和度的值不相同，因此，要根據含水飽和度的分布計算流管滲流阻力。對單流管不同的微元進行分析，見圖9。

圖9 單流管滲流阻力分析圖

根據物質平衡原理和達西公式，流經每個微元的流量是相同的。即：

對于第一、二個微元，通過達西公式分析得：

同理，對第一、二和三、四個微元有：

綜合以上推導的公式，從第一個到第n 個微元的總阻力，也就是這一根流管的阻力為式（13）。

1.3.4 多流管的吸水量 根據達西公式：

可知，每根流管的吸水量和其滲流阻力成反比。總的滲流阻力為：

每根流管的吸水量為：

2 模型求解

根據Buckley-Leverett 水驅油理論，針對單流管，根據注入量可以計算出流管飽和度的分布，進而計算出口端的含水飽和度和產水量。考慮了非均質性的多流管求解時，由于各流管的飽和度在不斷變化，導致滲流阻力也在不斷變化，因此，需要根據阻力劈分各流管的注入量（圖10）。

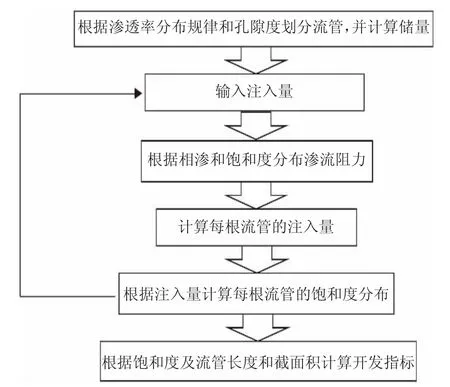
圖10 多流管模型求解步驟

對多流管模型進行了編程計算。應用BZ 油田的流體資料，根據威布爾分布對油田滲透率非均質性的描述，選用300 根流管，滲透率間隔選用20 mD，流管長度為300 m，每年注入速度為5%。模擬結果見圖11。

圖11 多流管驅替含油飽和度分布

圖11 中，左端為注入端，右端為產出端，橫向代表流管的滲流方向，顏色代表含油飽和度。可以看出，由于滲透率的非均質性，高滲條帶含水率推進速度比較快，對應的吸水量也更多。

3 應用成果

采用均質模型，分別用流管法、FRONTSIM 流線模擬器和E100 黑油模擬器模擬了水平井組一注一采的情況，三個模型物質基礎一致。計算結果表明三種方法曲線整體基本一致，物產相對誤差小于5%，證明流管法計算結果具有良好的精度（圖12）。

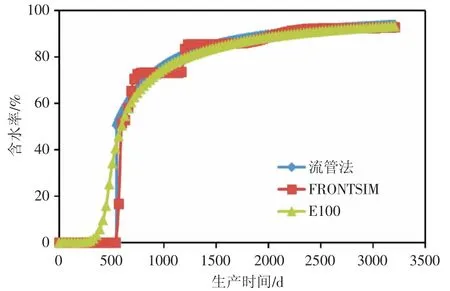
圖12 三種方法含水率計算結果對比圖

診斷井組開發效果常用的曲線為采出程度和含水率的關系曲線（圖13）。根據井組的儲量、有效厚度、水平段長度、流體特點，借用油田的非均質性資料，對BZ油田1167 砂體A35H 和A42H 井組的采出程度和含水率的關系曲線進行預測，并與實際生產情況進行對比[12－13]。

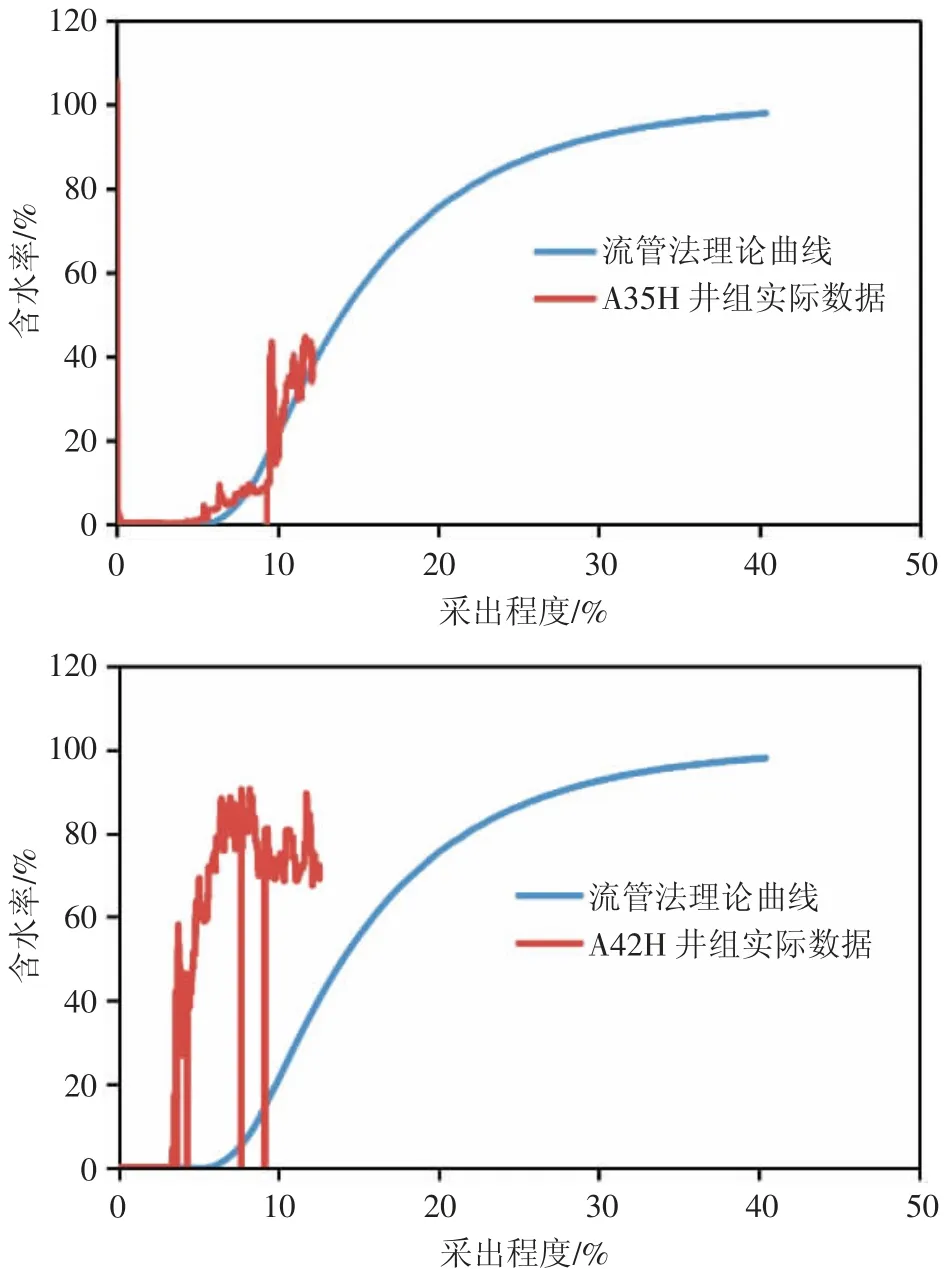
圖13 A35H、A42H 井組采出程度和含水率曲線

A35H 井組開發效果比較好，和理論曲線基本重合，證明流管法理論的正確性。A42H 井組與理論曲線有一定偏離，開發效果偏差，這說明井組可能存在高滲通道。為了驗證判斷，對比A42H 井組的示蹤劑檢測結果。

A42H 井組于5 月26 日注入示蹤劑，該井組于7月5 日見示蹤劑，見劑時間為40 d 左右。該井組見劑截至8 月13 日，整個峰值持續39 d，說明A42H 井組存在高滲通道，證明了流管法的判斷。

4 結論

（1）從流管法的基本理論出發，通過編程求解了單流管的模型。

（2）通過威布爾分布對油藏滲透率的非均質性進行了描述，提出了實際井組與多流管模型的轉化方法。使用編程求解了多流管模型。方便快捷的半解析模型對井組本來的開發規律進行了比較精確的理論描述。

（3）利用多流管模型對BZ 油田的A35H 和A42H兩個井組進行了開發效果評價，A35H 井組和多流管模型計算結果十分吻合，證明了計算模型的正確性；模型計算結果表明A42H 井組可能存在高滲通道，該結果與示蹤劑檢測結果相一致。