基于改進UKF 的非線性結構荷載和參數同步識別?

王 振，辛 宇，2，王佐才，2，袁子青

（1.合肥工業大學土木與水利工程學院 合肥，230009）（2.安徽省基礎設施安全檢測與監測工程實驗室 合肥，230009）

引言

工程結構在服役期間會遭遇各類不同的荷載激勵，當結構處于較低水平荷載激勵時，結構的行為符合線彈性假定［1］。然而，當其遭遇地震、強風等強荷載激勵時，結構在一定程度上表現出較強的非線性動力學行為，其振動響應也表現出非平穩特性。利用基于振動響應的健康監測技術識別非線性結構的特征參數，不僅為非線性結構的損傷診斷提供重要支撐，同時對結構的安全評估具有重要意義［2-3］。然而在實際應用中，對于隨機性較強的地震荷載，往往難以利用傳感器設備精確獲得結構外荷載的全部特征。因此，如何在輸入荷載未知的情況下，開展非線性結構參數識別已成為結構健康監測領域亟待解決的一個難題。

近年來，國內外學者在未知荷載作用下結構參數識別研究領域已取得一定的成果。李杰等［4］將結構基底作用力作為識別過程的修正因子，提出全量補償法和統計平均算法，并利用結構的動力響應數據識別出系統的物理參數，并反演地震動輸入。Lu等［5］利用基于動態響應靈敏度的模型修正方法實現了對外荷載及系統參數的同步識別。Chen 等［6］提出了一種具有修正功能的迭代識別方法，將外部激勵的空間信息轉化為數學條件，通過運動方程對未知力矢量進行預測和修正，再基于修正后的輸入力矢量對結構參數進行估計，并利用數值模擬驗證了該方法的可行性。但當外荷載激勵較強時，結構往往表現出非線性行為，此時上述線性系統識別方法將不再適用。

隨著擴展卡爾曼濾波（extended Kalman filter，簡稱EKF）［7］和UKF 方法［8］的提出，基于時域信號的非線性結構參數識別技術得到了快速發展。相較于EKF，UKF 以無跡變換來近似計算非線性系統狀態的后驗均值和協方差，有效避免了雅克比矩陣的計算問題，顯著提高了計算效率，并且在強非線性模型參數識別方面表現出優越性［9］。因此，在非線性系統識別中，UKF 方法得到了廣泛應用［10-11］。文獻 ［12-14］提出了一種基于UKF 的兩階段識別方法，首先利用最小二乘算法估計系統的外部荷載和子結構參數，再進一步結合傳統UKF 方法對系統的非線性參數進行識別。盡管該方法能夠實現未知激勵下的非線性系統識別，但需要將系統的全部動力響應作為觀測量。Ding 等［15］通過正交多項式對未知激勵進行分解，并將正交多項式的系數作為未知參數進行識別，但該方法需要識別的未知參數數量過多，導致其計算效率較低。為了實現非線性參數和未知激勵的同步識別，文獻［16-17］提出了一種基于改進UKF 的非線性系統識別方法，利用遞歸非線性最小二乘方法對未知激勵進行同步更新，能夠有效地實現非線性系統參數和未知激勵的同步識別，但當測量噪聲水平較高時，該方法往往難以收斂到真實值。

筆者在傳統UKF 方法的基礎上，提出了一種改進UKF 的荷載和參數識別方法，能夠有效實現結構狀態參數與未知輸入的同步識別。此外，為了降低測量噪聲的影響，改善濾波器的跟蹤性能，本研究進一步在提出的UKF 框架中嵌入線形卡爾曼濾波器，對測量噪聲協方差矩陣進行同步優化。通過數值模擬驗證了方法的可行性和精確性。

1 UKF 算法流程

假定離散非線性系統為

其中：k為離散時間；f(·)為非線性狀態方程；h(·)為非線性測量函數；Xk為n維系統狀態向量；zk為m維測量向量；uk-1為輸入向量；vk～N(0，Qk)為過程噪聲，服從高斯分布；wk～N(0，Rk)為觀測噪聲，服從高斯分布。

基于式（1）的UKF 狀態估計過程如下。

1）初始化系統狀態統計特性

2）選擇采樣策略，并計算sigma 點ξi，k-1(i=0，1，…，2n)，即

3）時間更新

4）測量更新

上述計算過程中的參數取值為

其中：λ=α2(n+κ)-n，α（0 ≤α≤1）為比例縮放因子，對于強非線性系統，α通常取一個較小的值；κ為比例參數，一般取κ=3-n或0；β為非權重系數，如果是高斯分布，β=2 為最優值；n為狀態變量維數。

2 基于改進UKF 的非線性結構荷載及參數同步識別

2.1 荷載及參數同步識別方法

對于具有多自由度的非線性系統，其運動方程可表示為

其中：M，C分別為結構的質量矩陣和阻尼矩陣；分別為結構的位移、速度、加速度響應向量；θ為未知結構參數向量；R(x，θ)為系統恢復力；u為外荷載；L為荷載分布向量。

在輸入荷載未知情況下，使用UKF 方法對結構狀態和參數進行同步識別時，在k時間步，狀態量更新完成后，采用預測狀態量和測量值結合運動方程，對未知輸入進行估計，即

其中：o 和p 分別為測量值和預測值；G(·)為非線性函數，G(·)中包含預估參數，需要在每一步進行更新。

在時間更新步中，利用k-1 步狀態量Xk-1和輸入uk-1，對k步狀態進行預測，將狀態預測值和測量值代入式（16）中，即可得到uk的估計值。將uk估計值代入到式（7）、式（8）中，即可求得測量預測值。此時得到的荷載估計值uk是不準確的，因為在uk的估計過程中，所使用的系統狀態量和參數均為預測值，在后續計算中，估計誤差將會被納入到測量噪聲中。

使用更新后的系統狀態和參數對未知輸入進行修正，即

用更新后的uk替換掉初始估計值，并在下一步預測中使用，重復上述過程，直至所有迭代全部完成。

具體識別流程如下。

1）初始化系統狀態統計特性

2）計算sigma 點ξi，k-1(i=0，1，…，2n)

3）時間更新和未知輸入估計

4）測量更新和未知輸入更新

對于傳統的基于UKF 的系統參數識別方法，測量噪聲和過程噪聲參數的協方差矩陣通常基于工程師經驗進行設定，當這些假定的協方差矩陣與真實值差別較大時，可能會導致識別結果不準確甚至發散。為降低測量噪聲對非線性系統識別的影響，本研究在進行荷載和參數的同步識別中，通過在UKF方法中嵌入KF 過程以實時優化測量噪聲矩陣［18］，有效實現了非線性系統參數與未知輸入的同步識別。KF 具體流程如下。

1）計算殘差序列和殘差序列協方差，即

2）KF 預測步。第k步測量噪聲e的先驗估計值和協方差為

其中：T為內嵌卡爾曼濾波過程的過程噪聲協方差矩陣。

觀測誤差協方差矩陣的對角線為

3）KF 更新步。KF 的預測協方差和互協方差矩陣為

其中：U為內嵌卡爾曼濾波過程的觀測噪聲協方差矩陣。

KF 的卡爾曼濾波增益為

e的后驗估計均值為

e的后驗估計協方差矩陣為

觀測噪聲預測值為

T和U也是零均值高斯白噪聲。將每次更新后的Rk代入到主濾波程序中，即可實現對噪聲的自適應調整。

2.2 識別結果評價指標

為了驗證未知激勵識別的有效性，本研究通過定義相關系數來量化未知荷載的識別精度。相關系數的表達式為

其中：l為樣本個數；yi為理論值；xi為識別值；為相應平均值。

相關系數r越接近于1，說明識別結果越接近于真實值。此外，基于先前研究結果［19］，當相關系數大于0.7 時，表明變量之間具有較好的相似性。

3 數值仿真分析

3.1 單自由度Bouc-Wen 模型算例

地震荷載作用下的單自由度Bouc-Wen 模型如圖1 所示，其運動方程為

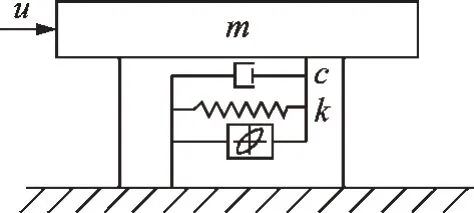
圖1 單自由度Bouc-Wen 模型Fig.1 The single degree of freedom Bouc-Wen model

其中：u為地震激勵；m，c分別為結構的質量和阻尼；x分別為結構的位移、速度和加速度；R(x，z，t)為系統恢復力；z為結構滯回位移。

Bouc-Wen 模型可以表示為

其中：k為結構剛度；α，β，γ，n為非線性參數。

本算例所用參數的數值如下：m=1 000 kg；c=0.3 (kN·s)/m；k=9 kN/m；α=0.1；β=2；γ=1；n=2。地震激勵選用1940 年的El Centro 地震波，持續時間為30 s，采樣頻率為50 Hz。

本研究利用4 階龍格庫塔方法對式（43）狀態方程進行求解，獲取結構理論位移、速度和加速度響應。將結構的加速度和位移響應作為觀測數據，并加入5%的高斯白噪聲模擬測量噪聲的影響。假設該系統的激勵未知，選取k，α，β及γ作為模型的未知參數，將未知參數寫入狀態變量中，得到系統的廣義狀態向量，其狀態空間方程式為

為了對未知系統的輸入和參數進行同步識別，系統參數的初始值設置如下：X0=[x0，，z0，k0，α0，β0，γ0]T=[0，0，0，5.4，0.06，1.2，0.8]T；Q0=10-8I7×7；I為單位矩陣 ；R0=diag(1，10-3)。利用筆者提出的改進UKF 方法對該滯回系統進行識別，Bouc-Wen 模型的參數識別結果如表1 所示。將滯回模型參數歸一化，非線性參數識別結果如圖2 所示。由表1 可知，在激勵未知條件下，改進的UKF 方法能夠實現Bouc-Wen模型參數的準確識別，識別誤差均低于3.2%。地震荷載和Bouc-Wen 模型滯回曲線的識別結果分別如圖3，4 所示。由圖3 可知，未知激勵的識別結果與真實值基本一致，且相關系數的計算值為0.96，說明未知激勵的識別結果具有較高精度。基于該單自由度Bouc-Wen 模型的識別結果可知，在輸入未知條件下，本研究所提方法能夠準確地實現非線性系統參數和外荷載的同步識別。

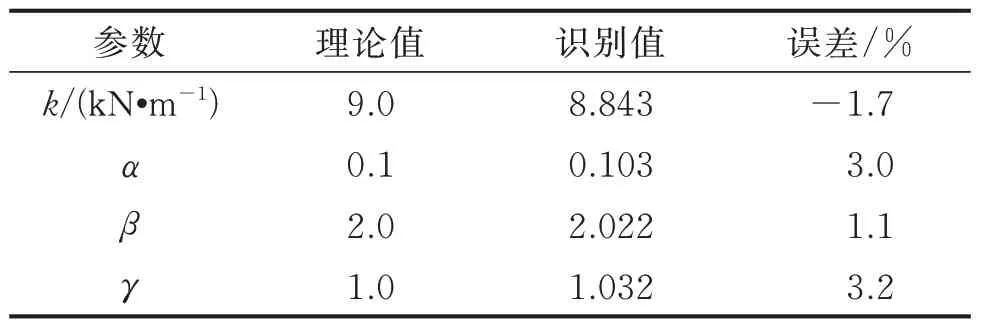
表1 Bouc-Wen 模型的參數識別結果Tab.1 The identified parameters of Bouc-Wen model

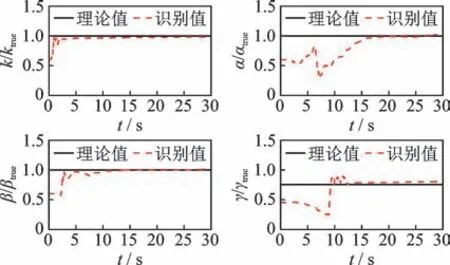
圖2 非線性參數識別結果Fig.2 The identified results of nonlinear parameters

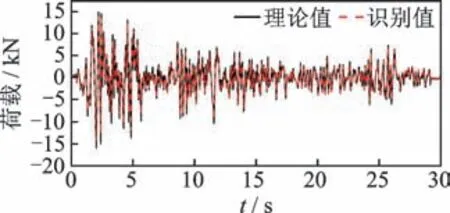
圖3 地震荷載識別結果Fig.3 The identified results of unknown seismic loads

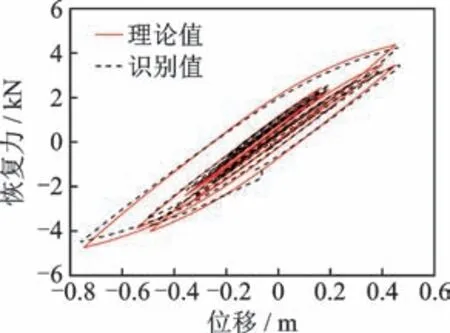
圖4 Bouc-Wen 模型滯回曲線識別結果Fig.4 The identified hysteric loop of Bouc-Wen model

為研究觀測量對識別結果的影響，分別對2 種工況進行討論：①僅加速度響應已知；②加速度和位移響應同時已知。利用所提的改進UKF 方法分別對2 種工況下的參數及未知激勵進行同步識別，并對比在不同觀測量組合下的參數識別結果和荷載識別結果，分別如表2 和圖5 所示所示。由表2 可知：在工況1 下非線性參數的最大識別誤差為7.7%；當加速度和位移響應同時作為已知觀測量時，非線性參數最大識別誤差僅為3.2%，識別精度顯著高于工況1 的結果。由圖5 可知：當僅把加速度響應作為已知觀測量時，識別的外部激勵在時間序列后半段出現飄移，相關系數計算結果為0.91，這是因為當僅以加速度響應作為觀測量時，由于積分誤差逐步累積，導致識別過程不穩定；當同時采用加速度和位移響應作為觀測量時，識別的外部激勵與真實值基本一致，識別精度較高。

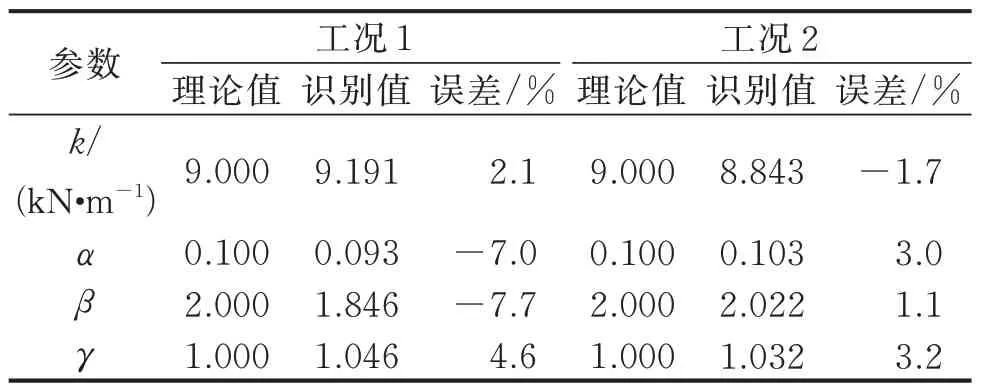
表2 不同觀測量組合下的參數識別結果Tab.2 The identified parameters under the different combinations of observations

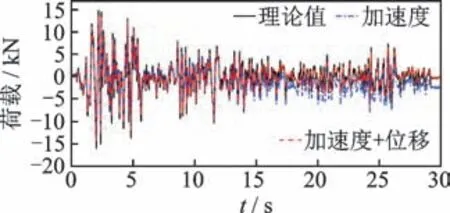
圖5 不同觀測量組合下的荷載識別結果Fig.5 The identified unknown loads under the different combinations of observations

為了驗證測量噪聲協方差矩陣的更新對識別結果精確性的影響，筆者以單自由度非線性系統為例，對有/無測量噪聲矩陣更新的2 種工況進行計算，其中工況1 為本研究所提出的改進UKF 方法，工況2為不考慮測量噪聲協方差矩陣更新。2 種不同工況下的參數及荷載識別結果分別如表3 和圖6 所示。由表3 和圖6 可知，2 種工況下，非線性參數和輸入荷載的識別結果均具有較高的精度。但由相關系數的計算結果可知，當不考慮測量噪聲協方差矩陣的實時更新時，相關系數的計算結果為0.93，低于工況1 的計算結果0.96。因此，通過對噪聲協方差矩陣進行實時更新，能夠提高非線性系統的識別精度。

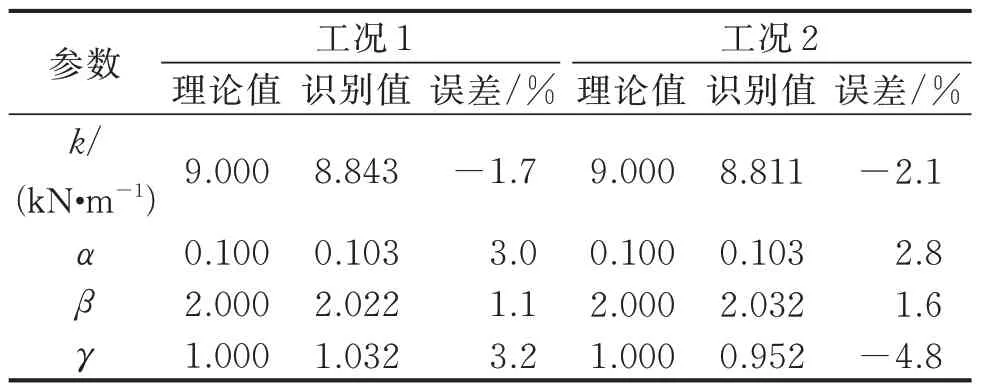
表3 2 種不同工況下的參數識別結果Tab.3 The identified parameters under the two different cases

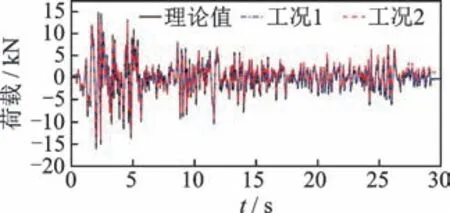
圖6 2 種不同工況下的荷載識別結果Fig.6 The identified unknown loads under the two different cases

為驗證本研究方法在非線性系統和未知荷載同步識別方面的優越性，將識別結果與UKF-UI算法［16］進行了對比。不同算法下非線性參數及荷載識別結果分別如表4 和圖7 所示。由結果可知，2 種方法均能實現未知荷載作用下的非線性系統識別，識別值與理論值吻合較好，相關系數均為0.96，但本研究方法的參數識別精度略高于UKFUI 方法。此外，由于UKF-UI 方法采用了迭代最小二乘算法對未知激勵進行估計，計算效率相對較低。

表4 不同算法下非線性參數識別結果Tab.4 The identified nonlinear parameters based on the different methods

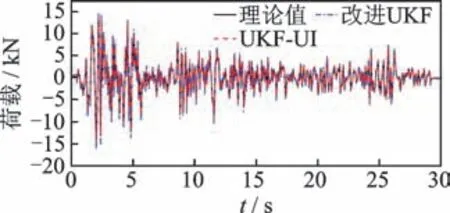
圖7 不同算法下荷載識別結果Fig.7 The identified unknown loads based on the different methods

3.2 5 自由度非線性系統

為進一步驗證改進UKF 方法對多自由度非線性系統識別的有效性，對某地震激勵作用下的5 自由度Bouc-Wen 模型進行數值模擬，5 自由度非線性結構系統如圖8 所示。在地震荷載作用下，該非線性系統的運動方程為

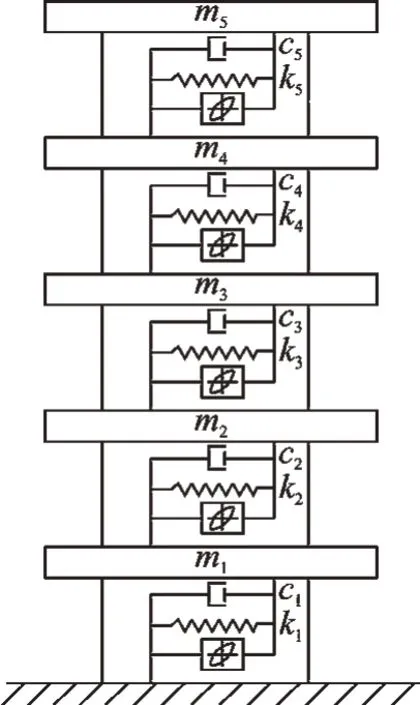
圖8 5 自由度非線性結構系統Fig.8 The five degrees of freedom nonlinear structural system

其中：M，C分別為剛度矩陣和阻尼矩陣；R(x，z，t)為系統恢復力；u為外荷載；L為荷載分布向量。

5 層Bouc-Wen 模型設計參數如表5 所示，地震激勵選用1940 年的El Centro 地震波，持續時間為30 s，采樣頻率為50 Hz。

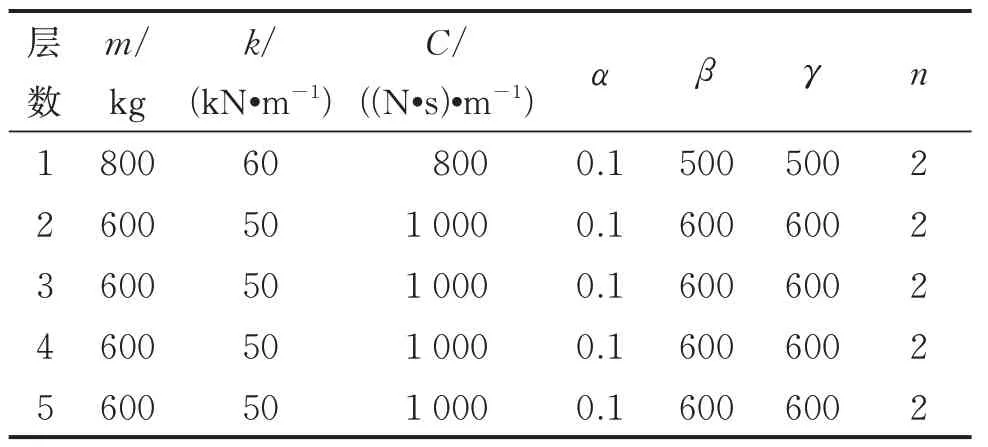
表5 5 層Bouc-Wen 模型設計參數Tab.5 The design parameters of five-storey Bouc-Wen model

將結構各層位移S、速度、滯回位移z、剛度k以及非線性參數α，β，γ寫入狀態向量，得到系統廣義狀態向量。該非線性系統和狀態空間方程為

其中：A=(α1，α2，α3，α4，α5)T；B=(1-α1，1-α2，1-α3，1-α4，1-α5)T；。

選取各層加速度響應作為觀測量，為避免由于積分誤差所引起的荷載識別漂移現象，本算例將第4 層位移響應作為已知觀測量用于系統識別。此外，為模擬測量噪聲對識別結果的影響，分別對已知的加速度和位移響應加入5%的高斯白噪聲，并基于改進的UKF 方法對未知激勵作用下的非線性系統進行識別。5 自由度非線性模型參數識別結果如表6 所示，底層和第3 層非線性參數識別結果如圖9所示，未知荷載識別結果如圖10 所示。對比表6 和圖9 可知，利用改進的UKF 方法能夠精確識別該非線性系統參數，且最大識別誤差低于5%。由圖10可知，未知荷載識別結果與真實值吻合較好，相關系數為0.98。底層滯回曲線識別結果如圖11 所示，由圖可知，基于改進的UKF 方法，結構在地震作用下的非線性力學行為能夠被準確識別。綜上所述，本研究所提出的改進UKF 方法能夠對多自由度非線性結構參數和未知激勵進行同步識別。

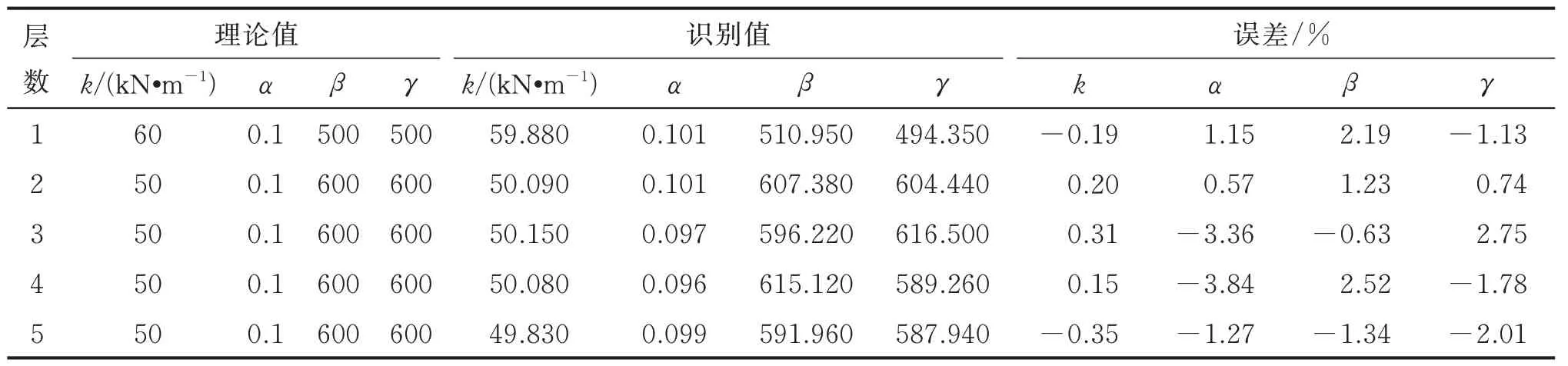
表6 5 自由度非線性模型參數識別結果Tab.6 The identified parameters of the five-DOF nonlinear model

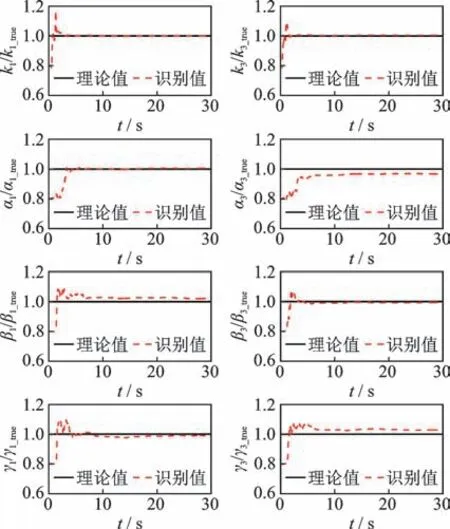
圖9 底層和第3 層非線性參數識別結果Fig.9 The identified nonlinear parameters of the 1st and 3rd floors

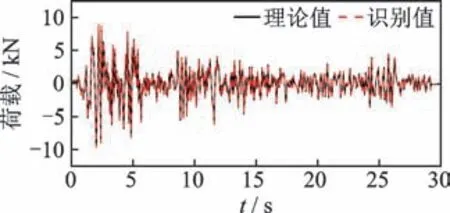
圖10 未知荷載識別結果Fig.10 The identified results of unknown loads

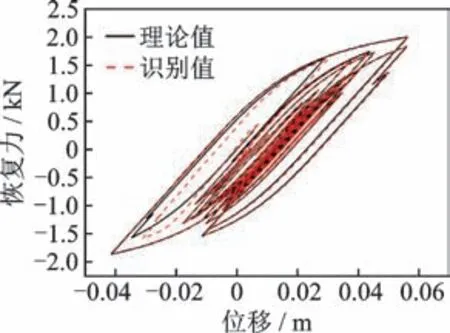
圖11 底層滯回曲線識別結果Fig.11 The identified hysteric loop of the 1st floor

4 結束語

提出了一種基于改進UKF 的非線性參數和荷載同步識別方法。該方法在系統狀態更新過程中，利用結構響應和參數的當前預測值，對輸入荷載進行初步估計，并進一步結合系統狀態的估計值對輸入荷載進行識別。為降低測量噪聲對非線性系統識別結果的影響，在UKF 方法中嵌入卡爾曼濾波器對測量噪聲協方差矩陣進行同步優化，確保了非線性結構荷載和參數識別的精確性。為了驗證該方法的可行性和準確性，分別對地震激勵下的單自由度和5 自由度Bouc-Wen 模型進行數值模擬。模擬結果表明，所提出的改進UKF 方法能夠對非線性系統參數進行可靠識別，對隨機輸入可進行同步估計。此外，由于測量噪聲矩陣在系統狀態估計過程中被實時更新，因此該方法具有較好的噪聲魯棒性。