不確定條件下的多目標件選擇性拆卸序列規劃模型

王菊梅

（廣安職業技術學院智能制造與汽車工程學院，四川 廣安 638000）

隨著政府對報廢汽車回收工作的支持力度不斷加大，報廢汽車回收量也與日俱增。由廢舊汽車產品所帶來的環境問題和其蘊含的經濟價值，凸顯了拆卸在理論研究和實踐中的重要性。

不同于裝配階段，產品在整個生命周期中由于所使用的環境、時長以及操作人員操作的不同，拆卸效率和收益會因回收產品質量狀況的不同而產生變化。

選擇性拆卸序列規劃是指通過拆卸操作，將零部件或裝配體從產品中分離出來，根據形成的所有可行序列，再通過某個或多個目標要求獲取最優或次最優的拆卸序列[1]。Geiger D 等[2]采用Bayesian 網絡的概率推理機制建立了每個拆卸操作的概率分布，利用計算機編程獲取拆卸成本和環境影響；Kongar E 等[3]以模糊理論為基礎，建立了以解決拆卸系統不確定的多目標優化模型；汪開普等[4]針對拆卸實際的復雜性，考慮模糊作業時間的多目標拆卸線平衡問題的數學模型；溫海駿等[5]為減少再制造拆卸過程中不確定因素的影響,采用模糊綜合評價法進行了回收質量等級劃分，然后采用雙重模糊變量描述了回收發動機質量狀況差異及拆卸時間的不確定性；陳弋文等[6，7]將零部件質量不確定性、拆卸破壞率、基本拆卸時間隨機等因素進行綜合考慮,建立了不確定環境下的拆卸收益模型，考慮到模型中存在的隨機變量和概率問題，選擇利用隨機模擬方法來設計相應的求解算法；Tian G 等[8]在建立的隨機拆卸網絡圖的基礎上，結合不同的拆卸決策準則，將每個移除操作或移除任務假定為具有一定概率的活動或事件，并且基于該假設條件確定拆卸過程的最優路徑；黃偉鑫等[9]假設可回收產品數量、單位回收產品拆卸時間以及單位零部件再制造加工時間為模糊變量，建立了模糊混合整數規劃模型，運用可信性理論將模型轉化為清晰等價形式；Behdad S 等[10]考慮不確定的時間，成本和造成損壞的可能性，將隨機規劃模型和通過沉浸式仿真獲得的信息一起應用來確定最優拆卸序列。

綜上，學者們的研究還處在不確定條件下的完全拆卸或部分拆卸序列規劃，但針對不確定下的多目標件選擇性的數學建模求解準確度不盡人意。文章著眼廢舊汽車產品零部件質量狀態和連接關系失效不確定性因素對拆卸過程的影響，最大化資源的可持續利用。

2 多目標件拆卸信息模型的構建

基于產品CAD 模型，通過人機交互的方式提取裝配關系，獲得零件和約束（接觸和非接觸空間約束）關系，綜合考慮拆卸連接關系和優先關系等信息。

混合圖模型相比于有向圖、無向圖模型來說能夠更加完整的描述產品拆卸信息，并且在一定程度上避免建模的組合爆炸問題，所以選擇拆卸混合圖來表達產品拆卸模型[2]。

混合圖G 主要由非空節點集合V、無向邊集合E和有向邊A 三元組構成，對于拆卸關系混合圖表示為：G=｛V，E，A｝。其中，V=｛v1，v2，…，vm｝是零件集合，m表示產品中零件的個數；E=｛e1，e2，…，en｝是無向邊集合，n 表示產品零件間連接關系的總個數；A=｛a1，a2，…，az｝是有向邊集合，z 表示零件間空間約束的總個數。由于給邊賦予了方向，那么對于有向邊az將與兩個相關聯的節點產生有序偶aij，其中i 和j 表示產品零件號。

基于混合圖G，可分解為連接關系圖Ge=｛V，E｝和優先關系圖Ga=｛V，A｝，可以直觀地表現出待拆零件間的連接關系和優先關系。利用生成的G 映射到鄰接矩陣GE和干涉矩陣GA來表達各零部件間的連接約束關系。

如果無向邊eij存在，則（i=1，2，…，m；j=1，2，…，m） 表示元素的連接關系，=1，即零件i 與零件j 連接；如果無向邊eij不存在，則=0，即零件i 和零件j 之間不存在連接關系。即

2 不確定條件下多目標件選擇性拆卸序列規劃數學模型的構建

2.1 模型假設

在進行拆卸序列規劃的過程中，根據實際的生產需求，為降低生產成本，構建了多目標件選擇性拆卸序列規劃數學模型，為便于求解，對問題進行了一定的簡化處理，考慮了如下假設：

2.1.1 拆卸順序為拆卸零件的次序，每一次拆卸操作表示從產品中拆除一個零部件，一次拆除多個零部件視為非規范操作。

2.1.2 緊固件等認為是拆卸約束和消耗品，忽略其剩余價值。

2.1.3 混合圖G 中所有節點都是不可分節點，這意味著每個組件都是最小的拆卸單元，當通過一次拆卸操作將零件拆卸后，所有和被拆卸零件有關的約束被視為全部解除。

2.1.4 零部件的基本拆卸時間、基本拆卸成本已知。在拆卸的過程中采用非破壞性拆卸，以盡可能確保零部件的完整性。破壞性的操作只針對失效連接的零件。

2.2 符號說明

2.2.1 集合

M：拆卸零部件(操作)數集合，其中M=｛i=1，2，…，m｝，m 為零件數；

O：目標零部件集合，其中O=｛o1，o2，…｝。

2.2.2 參數

i，j，k：零部件號；

Gij：零部件i 和j 的優先關系，如果i 優先于j 拆卸，Gij則為1，否則為0；

Ti：零部件i 的基本拆卸時間；

tij：零部件i 和j 的拆卸工具轉換時間；

gij：零部件i 和j 的拆卸方向轉換時間；

Ci：零部件i 的基本拆卸成本；

rij：零部件i 和j 的輔助拆卸成本；

max：一個極大數。

2.2.3 0～1 變量

xij：如果零部件i 和j 都拆卸且i 在j 前拆卸，則xij為1，否則為0；

yi：如果零部件i 已經被拆卸，則yi為1，否則為0；

hij：如果零部件i 和j 都被拆卸，則hij為1，否則為0。

2.2.4 連續變量

Si：零部件i 拆卸的開始時間。

2.3 模型的構建

為了更符合生產實際，將零部件質量狀態和連接關系失效不確定性考慮在內，以最小化拆卸成本作為優化拆卸序列的評價指標，分析拆卸過程中的不確定對選擇性拆卸序列規劃的影響，從而真實反映拆卸實際。

2.3.1 質量狀態不確定的表示及處理

在實際拆卸過程中，當零件質量狀態過低，其拆卸時間和價值已不能滿足拆卸操作所帶來的拆卸效率和費用，往往需要對其進行破壞性拆卸，如利用電鋸或其他特殊操作對該零件的連接關系進行切割分離，使之從產品中脫離出來。

Q=（q1，q2，…，qi，…，qm），其中qi表示零部件i 的質量狀態，主要通過專家經驗獲取。這里，對質量狀態過低的零件，認為零件質量失效，采用破壞性拆卸工具，則破壞性拆卸方式xi=1。當零件質量未失效時，采用常規拆卸方式xi=0。

將零部件質量狀態不確定用X 表示，X 是一個離散型隨機變量，表征零件質量失效與否，其分布規律服從0～1 分布，即X～B（1，P）。這里指因零件質量狀態低而采用破壞性拆卸的概率，則不發生破壞性拆卸的概率為（1-P），其分布律如表1 所示。

表1 X 的分布律

2.3.2 連接關系不確定的表示及處理

產品在經歷長時間的使用、維修等階段會導致零部件連接關系出現不同程度的失效。同樣，對連接關系的失效，考慮破壞性拆卸對拆卸過程的影響。這里，當連接關系失效就采用破壞性拆卸，否則常規性拆卸。將產品中零部件連接關系不確定用Y 表示，Y 是一個離散型隨機變量，表征連接關系失效與否，其分布規律服從0～1 分布，即Y～B（1，q）。這里指零部件間連接關系發生失效的概率，則不發生失效的概率為（1-q），其分布律如表2 所示。

表2 Y 的分布律

拆卸成本是拆卸序列規劃問題中的重要指標，也是企業在拆卸實踐中的重要需求，其目標函數如下：

式（5）表示拆卸成本主要包含基本拆卸成本和輔助拆卸成本。若因零件質量狀態采用破壞性拆卸方式，由于特殊勞動力、資源等的消耗，基本拆卸成本增加（Ci·yi·pi）；若因零件間連接關系失效而采用破壞性拆卸方式時，輔助拆卸成本增加（rij·xij·qij）。

式（6）表示目標函數，拆卸目標為最小化最大拆卸成本。拆卸成本越低，拆卸回收效益越好。為保證拆卸序列的可行性，還需要滿足下面的約束條件。

2.3.2.1 拆卸優先關系約束

式（7）表示當零件i 和j 存在拆卸優先關系時，僅當零件i 被拆卸之后，零件j 才可能被拆卸。

式（8）確保了所有的目標零件都必須進行拆卸操作。為對兩個決策變量進行約束，這里引進中間變量hij。

2.3.2.2 中間變量約束

式（9）～（11）表示當零件i 和j同時被拆卸，則變量hij為1。

式（12）和（13）表示若零件i 和零件j 都被拆卸，則變量和中必須有一個為1，且只能一個為1。

式（14）保證了序列中所有拆卸操作必須滿足優先關系約束，且不會形成“閉環”關系。

式（15）表示拆卸零部件的優先關系，當零件i 和零件j 都進行拆卸且i 在j 前拆卸。

式（16）和（17）表示對兩個決策變量進行線性化處理，當零部件i 和j 都被進行拆卸操作時，xij或xji才能成立。

2.3.2.3 時間關系約束

式（18）表示只有在前序零件已經被拆卸完成后才能開始其后序零件的拆卸操作。

通過上述公式（5）～（18）共同構成了不確定條件下的多目標件選擇性拆卸序列規劃的數學模型。

3 實例研究

為了驗證模型的有效性與準確性，文章參考了參考文獻［11］，同時針對該裝配體拆卸相關信息進行了搜集，其拆卸工具、方向、成本等拆卸相關信息如表3 所示。

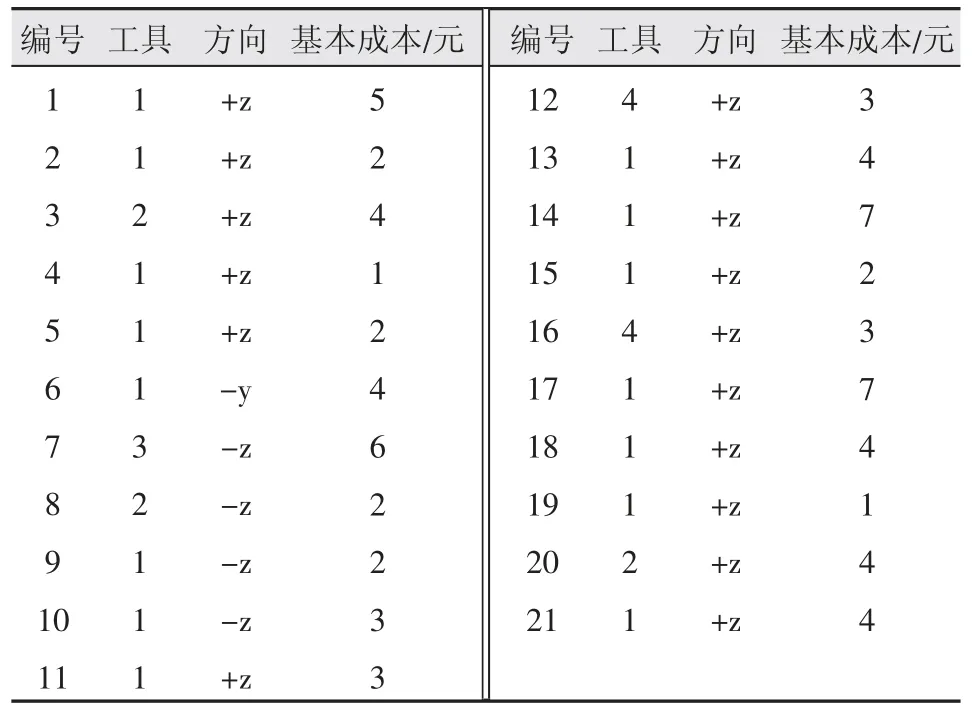
表3 拆卸相關信息

該裝配體主要包含了21 個零件，11 號零件和18 號零件是目標零件。根據上述多目標件拆卸信息模型的構建方法，其拆卸混合圖如圖1 所示。

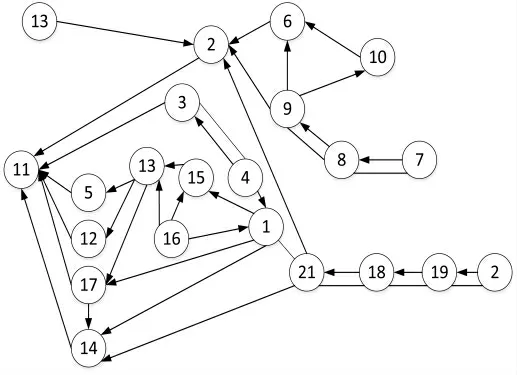
圖1 拆卸混合圖G

通常，拆卸時間與拆卸成本成正相關，假定其拆卸輔助成本是拆卸工具變換時間的0.5 倍。其拆卸工具轉換時間如表4 所示。

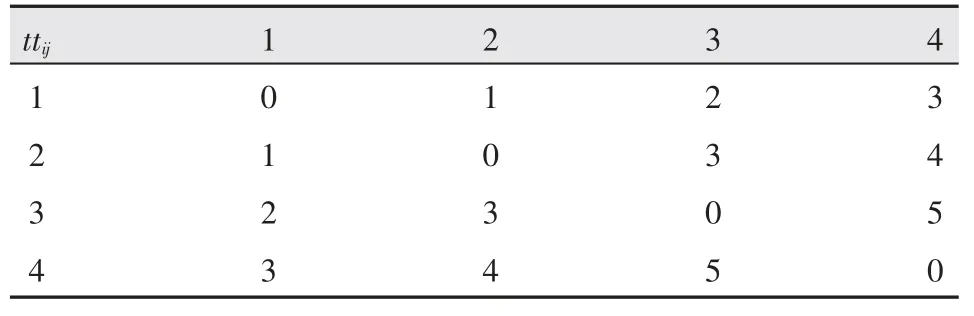
表4 拆卸工具轉換時間 s

受不確定的影響，零件質量狀態失效和連接關系的失效概率取值分別為0.2 和0.25，它們都服從獨立分布。

根據其拆卸相關信息，基于GAMS 平臺開發模型求解程序，拆卸序列規劃結果如表5 所示。從實驗結果顯示其最佳解決方案不止一個，這是因為復雜產品中的多目標件拆卸過程存在多個同等拆卸優先關系和拆卸成本的零件，在拆卸過程中選擇有多個，只要拆卸條件滿足即可。

表5 拆卸序列規劃結果

4 結論

針對回收再制造、再利用領域的拆卸序列規劃問題，考慮零件質量狀態和連接關系的不確定，建立了不確定條件下的最小化拆卸成本的多目標件拆卸序列規劃數學模型，同時基于GAMS 平臺開發模型程序，得到了可行拆卸序列，充分驗證了其可行性與有效性，對于生產實踐更加具有啟發性。