基于負載補償的功率分流混合動力系統模式切換性能測試方法*

李豪迪，趙治國，唐 鵬，侯永平

（同濟大學汽車學院，上海 201804）

前言

面對日益嚴重的能源危機和環境污染，混合動力電動汽車得到了快速發展［1］。使用功率分流混合動力專用變速器（dedicated hybrid transmission，DHT）的混合動力系統作為主流技術方案已得到產業化開發與應用［2-3］。考慮到功率分流混合動力系統從純電動向混合動力模式的切換包括發動機起動、模式切換元件動作以及動力源切換等多個瞬態過程［4-5］，切換過程高、低頻動力學特性復雜且控制難度大，開發高性能的模式切換協調控制策略已成為提高車輛駕駛平順性的關鍵［6］。通常模式切換控制策略先基于車輛縱向動力學離線仿真模型開發，之后采用高動態性能測試臺架對其進行優化、標定與驗證，但由于實際測試臺架與真實車輛傳動軸結構、動力源以及道路負載作用方式差異，導致所開發的切換控制策略在臺架測試時的適應性不足。因此，為縮短功率分流混合動力系統模式切換協調控制策略的測試時間，有必要開發一種基于真實車輛加載特性的臺架仿真模型，并進行測試臺架負載模擬補償，以實現功率分流混合動力系統模式切換性能模擬與策略驗證。

目前，研究人員針對電動汽車動力系統測試臺架模型進行了大量研究。Liu 等［7］開發了電力驅動系統試驗臺模型，該模型可用于研究電驅動系統的瞬態過程控制方法。Fajri 等［8］開發了車輛電驅動系統測試臺架模型，仿真結果表明該試驗臺模型具有較好的高速跟蹤精度。Karol等［9］提出了一種開發電機負載仿真控制策略的試驗臺模型，可以模擬電機的線性和非線性動態，減少電機動態性能的調試時間。可見，針對電驅動系統動態性能測試建立的測試臺架模型可實現良好的動態加載精度要求。然而，當測試臺架的傳動軸較長時，其轉動慣量、阻尼等參數誤差以及傳動軸的扭轉特性將惡化測試臺架的轉速閉環跟蹤性能，從而降低負載模擬加載精度。因此，需要搭建包含測試臺架傳動軸的測試臺架模型，以進一步探究其負載模擬加載特性和加載轉矩補償方法。

為提高測試臺架的負載模擬精度，現有研究多通過設計基于加載裝置轉速閉環跟蹤控制的補償器對其加載轉矩進行修正。Wang 等［10］針對雙電機履帶車輛測試臺架模型，采用轉速閉環跟蹤前饋補償控制方法對負載模擬裝置加載轉矩進行補償。Fajri等［11］采用雙電機測試臺架驗證了電動車輛等效集中慣量模型的轉速閉環跟蹤性能。Liu 等［12］針對混合動力系統開發了一種基于轉速自適應預測控制的負載模擬方法，該方法可降低模型參數不確定性對控制精度的影響。Akpolat 等［13］針對可編程測功機控制系統，設計了一種基于負載模擬轉速閉環跟蹤的轉速前饋補償控制器。Gan 等［14］設計了一種基于比例積分負載模擬轉速閉環控制器的轉速前饋補償器，以消除測試系統的機械特性。劉和平等［15］采用轉速閉環跟蹤矢量控制方法實現了純電動汽車測試臺架的轉動慣量補償。王冠峰等［16］提出了一種電驅動系統臺架試驗動態補償算法，采用卡爾曼濾波來實現模型誤差的精確補償。然而，功率分流混合動力系統相較于以上動力總成，其模式切換過程的發動機和電機動態協調響應精度受負載影響較大，傳統的轉速閉環跟蹤控制補償器難以滿足測試臺架更高的加載轉矩精度要求，致使模式切換過程動力源的動態特性測試準確度不高。

本文以功率分流混合動力系統性能測試臺架為研究對象，提出了一種基于負載動態補償的功率分流混合動力系統模式切換性能臺架測試方法。首先，建立測試臺架系統模型；其次，針對從純電動至功率分流混合動力模式切換過程，基于Matlab/Simulink-AMEsim 平臺搭建了測試臺架仿真模型，并對模式切換及加載性能進行分析；之后，設計負載模擬轉速閉環跟蹤控制器以及補償器；最后，對負載模擬補償方法的有效性進行仿真和試驗驗證。

1 測試臺架結構與動力學建模

1.1 測試臺架結構

功率分流混合動力系統性能測試臺架如圖1 所示，主要由模擬發動機、功率分流DHT、車橋、左/右傳動軸、測功機以及控制系統等組成，其中DHT 通過左/右傳動軸與測功機同軸連接，左/右傳動軸是通過多根傳動短軸以及膜片彈簧聯軸器串聯形成的剛柔耦合傳動長軸。功率分流DHT 由拉維娜式行星排（PGS）、MG1 與MG2 電機、B1 與B2 制動器等組成。

圖1 測試臺架結構

1.2 負載模擬動力學模型

測試臺架需要能夠模擬真實車輛行駛道路阻力矩，將負載模擬點等效至DHT 的動力輸出端，模擬車輛和功率分流DHT參數如表1所示。DHT的等效輸出端轉矩由輸出端轉速和加速踏板開度查表得到，如圖2所示。車輛行駛道路阻力矩為

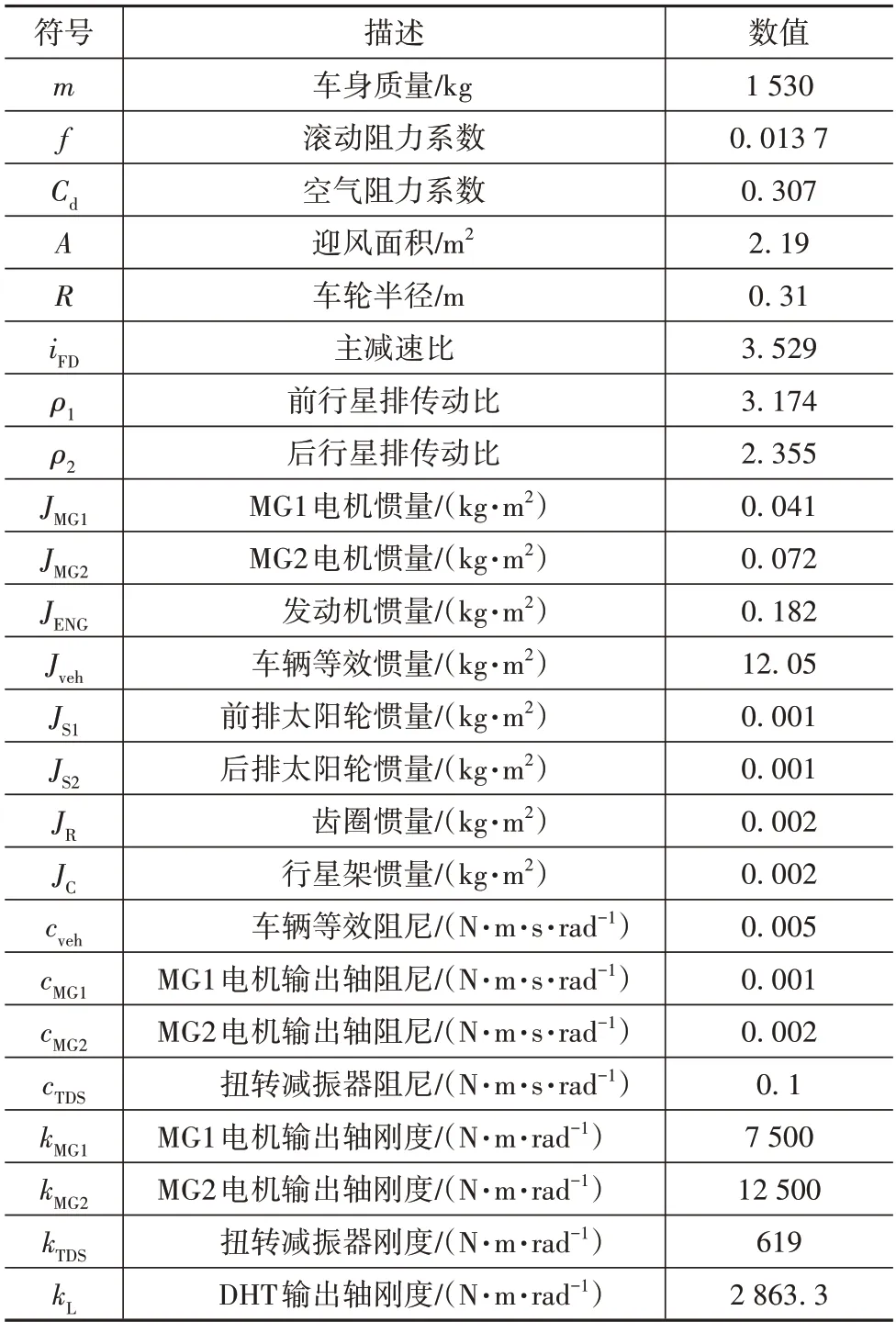
表1 模擬車輛和功率分流DHT參數

圖2 DHT等效輸出端轉矩查表

式中：Tv為真實車輛行駛道路阻力矩；m為整車質量；g為重力加速度；f為滾動阻力系數；θ為道路坡度；CD為空氣阻力系數；A為迎風面積；δ為旋轉質量換算系數；vveh為車速；R為車輪半徑。

加速踏板開度通過測功機轉速跟蹤車輛目標輪速求得：

式中：χ為加速踏板開度為比例系數為差分系數；ωveh為車輪目標角速度；ωem為測功機角速度。

車輪轉速根據車輛等效轉動慣量和阻尼計算得到：

式中：Tout為DHT輸出端等效驅動轉矩；Jveh和cveh分別為車輛的等效轉動慣量和等效阻尼。

式中：Jem和cem分別為測試臺架等效轉動慣量和等效阻尼為測試臺架加載轉矩。

1.3 模擬發動機模型

不考慮發動機內部復雜的物理及化學變化過程，采用1 階慣性環節模擬發動機驅動轉矩的動態響應特性：

式中：TENG_ob為發動機實際轉矩；τENG為發動機響應滯后時間；TENG為發動機目標轉矩。

1.4 DHT動力系統模型

DHT 內部集成的MG1 和MG2 電機為永磁同步電機，關鍵參數如表2 所示，為了可模擬其輸入和輸出特性（如轉速、轉矩、電流和效率等），本文建立電機控制系統模型［7］，經過坐標變換得到的電流方程為

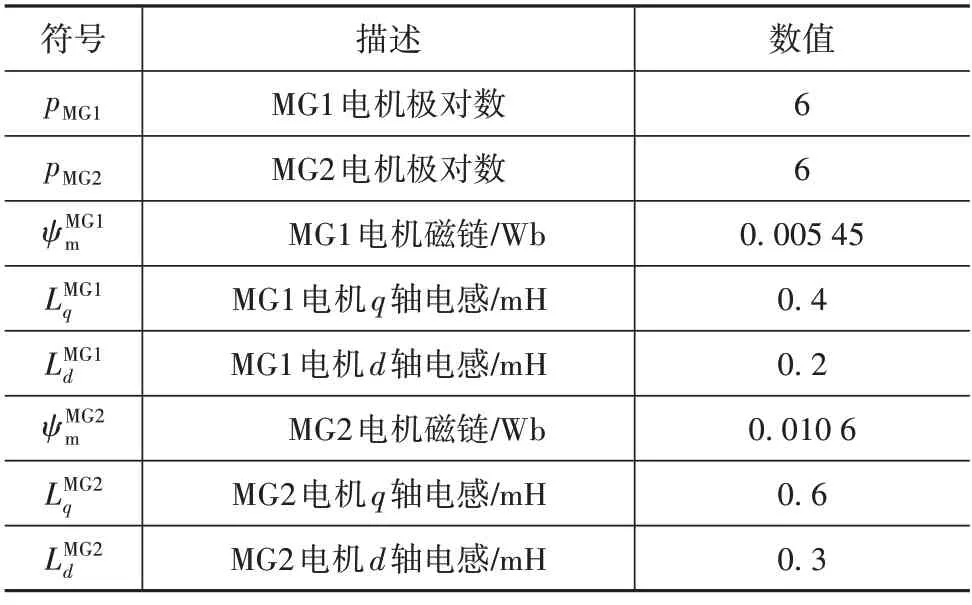
表2 電機關鍵參數

電機電磁轉矩方程為

電機機械運動方程為

將搭載功率分流DHT 的整車傳動系統等效為四彈性集中質量模型，如圖3 所示。其中，S1 和S2分別為前/后排太陽輪；P為行星輪；C為行星架；R為齒圈。

圖3 四彈性集中質量模型

四彈性集中質量模型的狀態空間表達式為

將MG1 電機轉矩TMG1、MG2 電機轉矩TMG2、發動機轉矩TENG和Tv作為系統輸入，結合式（7）可得：

其中：

1.5 測試臺架傳動系統模型

將臺架傳動系統等效為單軸4 自由度集中質量模型［17］，如圖4所示。

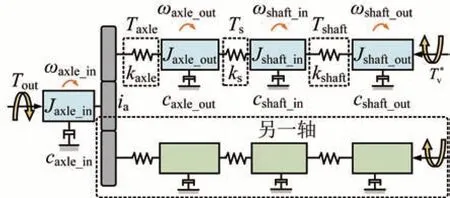
圖4 測試臺架傳動系統模型

建立測試臺架傳動系統動力學微分方程：

車橋傳遞的彈性轉矩為

車橋與剛柔耦合傳動軸連接點的傳遞轉矩為

剛柔耦合傳動軸的傳遞轉矩為

式中：J為轉動慣量；ω為等效角速度；c為阻尼；k為彈性系數；ia為車橋傳動比。

測試臺架加載轉矩為測功機的電磁轉矩，其與電流的關系為

式中：Np為極對數；msr為轉子磁通；Lr為轉子電感；Ird和Irq為定子d-q軸電流；Isd和Isq為轉子d-q軸電流。

2 模式切換臺架測試性能分析

2.1 模式切換過程分析

功率分流混合動力系統的工作模式如表3所示。

表3 功率分流混合動力系統工作模式

以純電動向功率分流模式切換為例，其協調控制流程如圖5 所示。車輛起動后首先進入純電動模式，當MG2電機需求轉矩Tveh超過其最大轉矩TEV_max、荷電狀態SOC低于閾值SOClow或車輛速度vveh超過閾值vEV_max時，制動器B1緩慢打開，利用MG1和MG2電機保證行駛平順性，在B1 完全斷開后，電機將發動機拖轉至怠速，發動機點火，進入功率分流模式，模式切換過程分為3 個階段：純電動模式、電機拖轉發動機階段和功率分流模式［4］。

圖5 模式切換協調控制流程

2.2 模式切換過程轉矩分配

2.2.1 純電動模式

純電動模式時，車輛僅由電機MG2 驅動，MG1的需求轉矩為零，DHT 的驅動轉矩用于MG2 轉矩計算：

當制動器B1 滑摩時，制動轉矩參與電機轉矩決策：

制動器B1的制動轉矩TB為

式中：n為制動器摩擦面數；μk為動摩擦因數；PB為摩擦片表面壓力；ro為外徑；ri為內徑。

2.2.2 拖轉發動機階段

當制動器B1 完全分離時，電機既要保證車輛正常行駛，又要提供額外的轉矩將發動機拖轉至怠速。其中，保證車輛正常行駛的電機目標驅動轉矩由DHT輸出端等效驅動轉矩計算得到：

另外，拖轉發動機至怠速過程的額外電機轉矩為

則拖轉發動機階段電機的目標轉矩為

2.2.3 功率分流模式

當發動機被電機拖轉到怠速時，發動機噴油，車輛切換到功率分流模式，發動機目標轉矩為

電機的目標轉矩為

2.3 模式切換及加載性能分析

功率分流混合動力系統模式切換性能臺架測試原理如圖6所示。

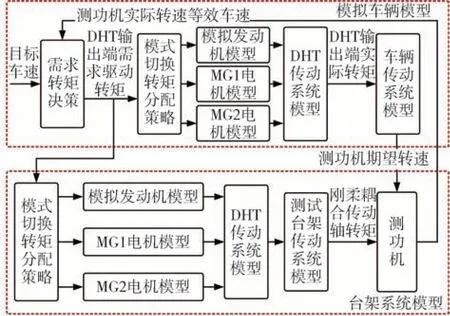
圖6 臺架測試原理

由圖7 可以看出拖轉發動機模式切換階段各動力源的輸出軸轉矩擬合趨勢較好，但存在動態誤差，說明基于模擬車輛模型開發的模式切換控制策略雖適用于臺架系統模型，但基于臺架系統模型的動力源動態響應特性與模擬車輛模型一致性不佳，控制精度需進一步提升。

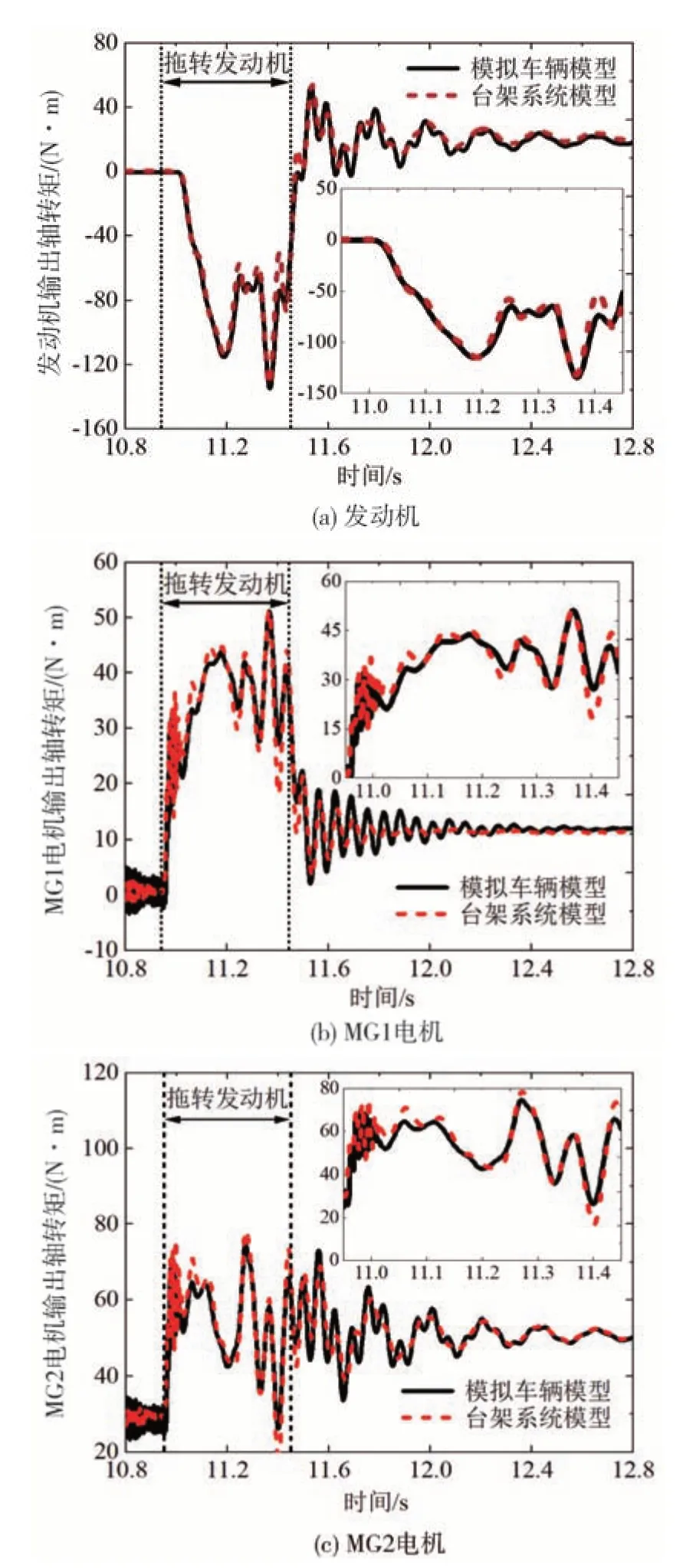
圖7 動力源輸出軸轉矩

由圖8 可以看出各動力源的轉速一致性較好，表明臺架系統模型對于轉速的模擬是有效的。然而，出現動力源動態響應差異的原因是測試臺架相較于實際車輛，其傳動系統慣量及阻尼等參數存在差異，致使負載模擬加載轉矩出現較大的動態誤差，如圖9 所示，使得測功機加載轉矩不能精確地模擬出實際車輛的真實道路負載，導致控制策略的適用性差，故須對加載轉矩進行補償修正。

圖8 動力源輸出軸轉速

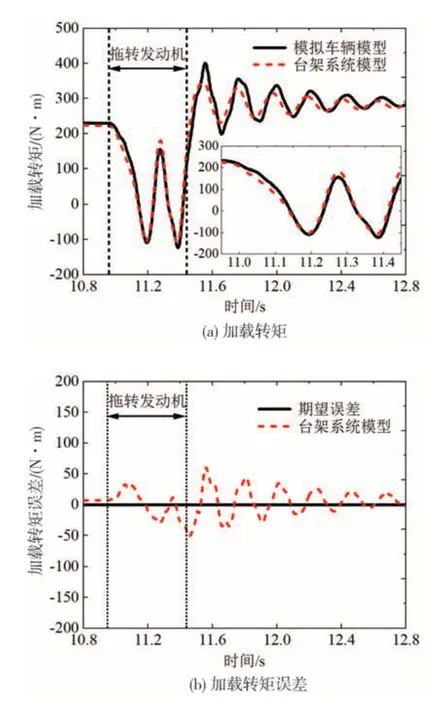
圖9 加載轉矩及誤差

3 測試臺架負載補償

3.1 轉速閉環跟蹤控制器設計

轉速閉環跟蹤控制器可保證測功機能精確模擬目標輪速，并實現測試臺架的運行穩定性，控制原理如圖10所示，其傳遞函數關系可表示為

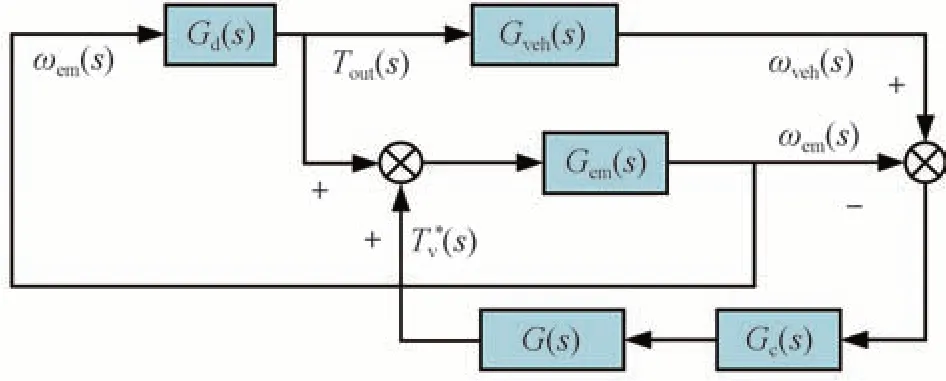
圖10 轉速閉環跟蹤控制方法

式中：Gem（s）為測試臺架傳動系統傳遞函數；G（s）為測功機電磁轉矩計算常數；Gc（s）為測功機轉速-電流控制環節；Gd（s）為DHT輸出端等效驅動轉矩解析環節。

若使式（33）實現理想的轉速跟蹤性能，即ωveh（s）=ωem（s），則Gd（s）Gem（s）=1。因此結合式（2）可將Gd（s）設計為

式中KT為DHT輸出端等效驅動轉矩系數。

同時，結合式（4）可將式（13）等效為

測功機的轉速跟蹤控制采用比例-積分-差分控制器，根據DHT驅動轉矩變化自適應調節電流：

因此，得到轉速閉環跟蹤的傳遞函數為

考慮Jem和cem參數的±25%擾動量，得到如圖11所示的轉速閉環跟蹤系統幅頻-相頻特性對比，可以看出在一定的帶寬內，參數擾動使得轉速閉環跟蹤控制器不可避免的存在振蕩，因此，必須通過設計恰當的補償器來抑制干擾，以提高測試臺架轉速閉環跟蹤控制的穩定性。

圖11 轉速閉環跟蹤系統相頻-幅頻特性

3.2 補償器設計

測試臺架傳動系統的摩擦、對中及扭振會惡化轉速閉環跟蹤性能。因此，在轉速閉環跟蹤控制器中引入轉速前饋校正補償器Gcomp（s），從而提高其抗干擾能力。同時，設計轉矩前饋校正補償器來減小加載轉矩響應滯后引起的動態誤差，其原理如圖12 所示。基于圖10 設計的轉速前饋校正補償器為

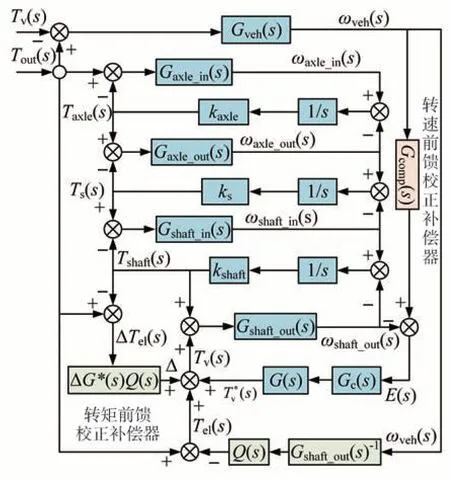
圖12 負載模擬補償控制方法

式中Gveh（s）為模擬車輛傳動系統傳遞函數。

由于Gcomp（s）中包含有車輛逆動力學模型Gveh（s）-1，其微分環節易引起系統的不穩定，因此將前饋校正補償器重新設計為

由式（41）可以看出該轉速前饋校正補償器，可通過調節增益使得相位滯后實現轉速閉環跟蹤系統穩定。通過對比兩種補償器的幅頻-相頻特性如圖13 所示，補償器Gd(s)Gem(s)具備抑制高頻的陷波作用，可有效提高測試臺架轉速閉環跟蹤控制器的穩定性。

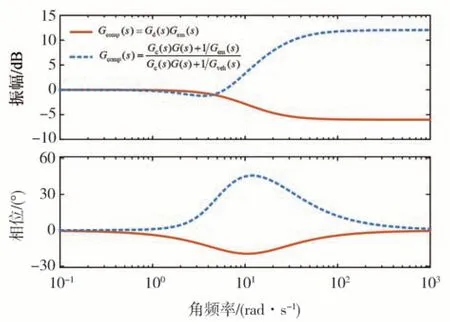
圖13 補償器幅頻-相頻特性對比

同時，轉速閉環跟蹤系統的穩定性對比如圖14所示，補償前的轉速閉環跟蹤特性由接近虛軸但又不十分接近零點的一對共軛主導極點S1=-0.2778+10.54i 和S2=-0.2778-10.54i 確定，轉速閉環跟蹤控制器的抗干擾能力差，而采用Gd(s)Gem(s)補償器校正后產生的新增極點遠離虛軸，可提高轉速閉環跟蹤控制器的穩定性。

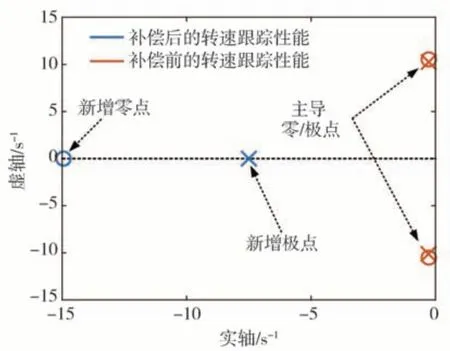
圖14 轉速閉環跟蹤性能對比

轉矩前饋校正補償器得到的加載轉矩補償量由可測補償量和不可測補償量兩部分組成組成。不可測部分轉矩補償量將通過模擬車輛車輪目標角速度ωveh（s）為狀態輸入，引入1/Gshaft_out（s）進行加載轉矩觀測，同時進行1 階低通濾波Q(s)=1/(τds+1)，得到加載轉矩補償量：

式中：τd為滯后時間；Tel（s）為不可測加載轉矩補償量。

結合圖4可將測試臺架傳動系統表示為

同時，通過實時采集轉矩傳感器信號對可測部分加載轉矩補償量進行計算：

引入動態調節增益對可測部分加載轉矩補償量進行調節，以消除測試臺架傳動系統參數攝動對加載轉矩精度的影響，可將其表示為

式中：Δ為可測部分補償量；ΔG*(s)為補償調節增益；Kf為參考補償增益；ΔKf為動態調節增益。

因此，得到加載轉矩補償量為

根據式（3）和式（4）得到補償后的關系式為

進而得到補償后的測試臺架負載模擬動力學關系為

4 仿真分析

采用Matlab/Simulink-AMEsim 聯合仿真平臺對臺架系統模型的準確性和負載動態補償方法的有效性進行驗證，由于模式切換初始車速和加速踏板開度影響DHT 動力輸出端驅動轉矩，因此將其設置為仿真變量。

4.1 不同模式切換初始車速

當臺架測功機轉速等效車速分別達到25、30 和35 km/h 時，開始進行模式切換，設置加速踏板開度為20%，結果如圖15～圖17 所示，結果統計如表4所示。

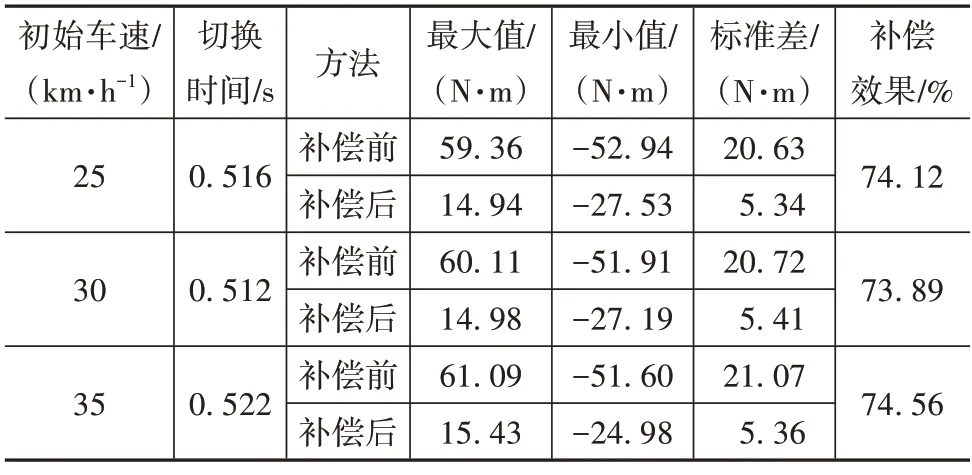
表4 不同初始車速仿真結果

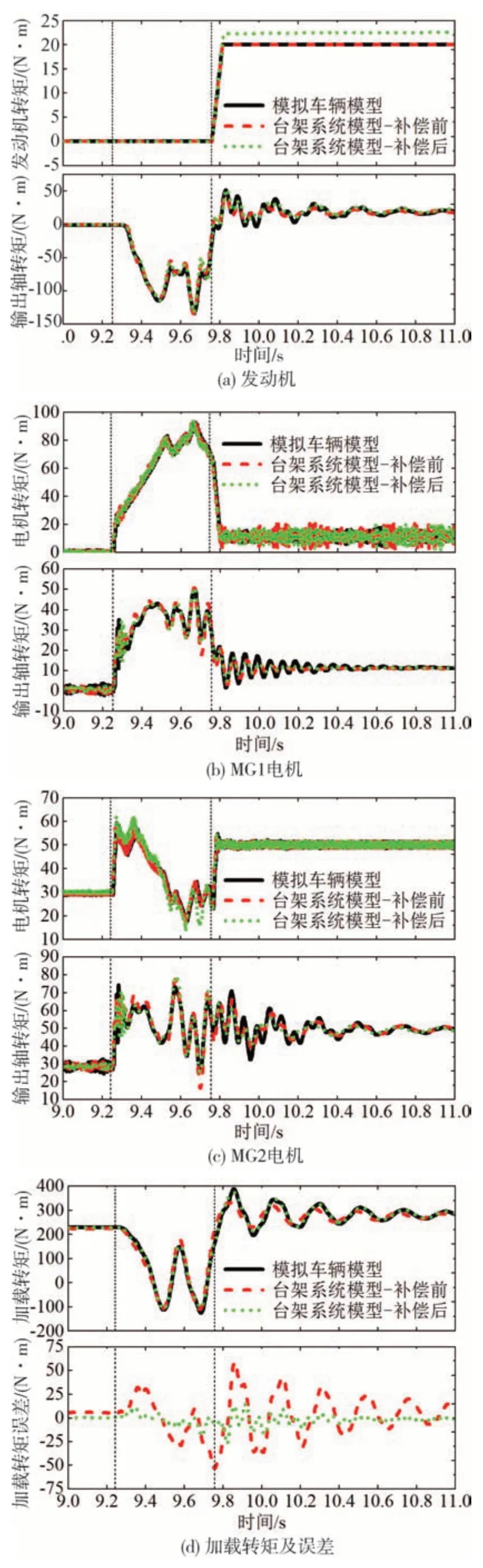
圖15 初始車速25 km/h

25 km/h 時的動力源轉矩和負載特性對比如圖15所示，其模式切換時間為0.516 s。由圖15（a）～圖15（c）可以看出動力源的目標轉矩補償效果明顯，并且補償后的輸出軸轉矩與模擬車輛模型擬合效果好，表明了所搭建的臺架系統模型的正確性，以及補償控制算法能夠有效保證動力源的動態輸出特性。由圖15（d）可以看出補償后的測試臺架加載轉矩與模擬車輛模型的行駛阻力矩具有較好的一致性，且加載轉矩誤差的標準差為5.34 N·m，好于補償前的20.63 N·m，加載轉矩精度提高了74.12%。因此，在初始車速25 km/h條件下，臺架系統模型具有較高的仿真精度，驗證了負載模擬動態補償控制方法的有效性。30 km/h 時的動力源轉矩和負載特性對比如圖16 所示，其模式切換時間為0.512 s。由圖16（a）～圖16（c）可以看出動力源的目標轉矩補償效果明顯，同時圖16（d）所示補償前加載轉矩誤差最大值為60.11 N·m，最小值為-51.91 N·m，標準差為20.72 N·m；而補償后的誤差最大值為14.98 N·m，最小值為-27.19 N·m，標準差為5.41 N·m，加載轉矩精度提高了73.89%。35 km/h 時的動力源轉矩和負載性能對比如圖17 所示，可以看出模式切換時間為0.522 s，加載轉矩精度提高了74.56%。以上結果表明在不同模式切換初始車速條件影響下，本文所提出的負載模擬補償控制算法具有魯棒性，可提高功率分流混合動力系統模式切換性能測試的準確性。

圖16 初始車速30 km/h

4.2 不同加速踏板開度

設置駕駛員加速踏板開度分別為25%、30%和35%，模式切換初始車速為20 km/h，結果如圖18～圖20 所示，結果統計如表5 所示。結果顯示補償后的臺架系統模型動力源動態響應曲線與模擬車輛模型保持一致，與不同模式切換初始車速條件下的結果相比也具備較好的補償控制性能，模式切換時間也較為接近。由圖18（d）看出補償后的加載轉矩最大值為16.85 N·m，最小值為-22.57 N·m，標準差為5.62 N·m，相較于補償前的17.52 N·m，加載轉矩精度提高了67.74%。由圖19（d）看出補償后的加載轉矩最大值為15.16 N·m，最小值為-20.34 N·m，標準差為5.05 N·m，相較于補償前的19.55 N·m，加載轉矩精度提高了71.175%。由圖20（d）看出補償后的加載轉矩最大值為12.49 N·m，最小值為-23.27 N·m，標準差為5.99 N·m，相較于補償前的14.36 N·m，加載轉矩精度提高了58.29%。不同加速踏板開度條件下仿真結果進一步表明了本文所提出的基于臺架系統模型的負載模擬補償控制算法的有效性和魯棒性。

表5 不同加速踏板開度仿真結果

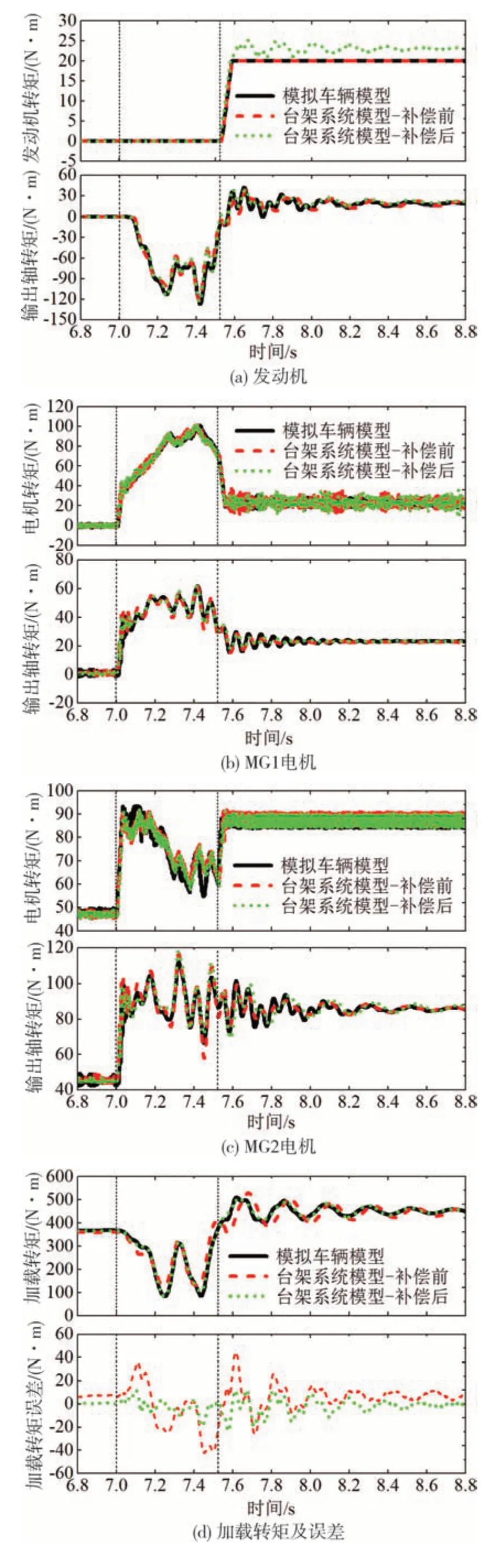
圖20 加速踏板開度χ=35%

5 試驗驗證

5.1 試驗環境

模式切換性能測試臺架環境如圖21 所示，主要由功率分流DHT 及其控制器、模擬發動機電機、轉矩/轉速傳感器、左/右傳動軸、車橋、測功機、供電系統、快速原型控制器和上位機等部件組成。電池模擬器通過CAN 總線實現與測功機通信交互并向混合動力系統提供直流電源，同時DHT 控制器和測功機通過CAN 總線與快速原型控制器通信，采用CANape 對測功機和DHT 進行實時監測。試驗基于Matlab 軟件和自動代碼生成技術，以C 代碼的形式下載至快速原型控制器。上位機通過標定協議與快速原型控制器通信，發送轉矩等指令至試驗臺架并接收轉速和轉矩等測量值。

圖21 實際測試臺架環境

5.2 試驗結果

圖22為功率分流混合動力系統模式切換過程動力源實際轉矩結果對比。圖中MG1 和MG2 電機轉矩為電機模型計算得到的電磁轉矩，而試驗轉矩為控制器反饋的實際轉矩，通過對比可以看出仿真與試驗轉矩的擬合效果良好，表明了模式切換控制策略在臺架測試時具有良好的適應性，但由于控制器的采樣頻率僅為200 Hz，小于電機模型的10 000 Hz計算頻率，因此，電機仿真轉矩更能反映模式切換過程中電機的高頻響應特性。圖23為動力源實際轉速結果對比，可以看出動力源轉速曲線一致性較好，進一步驗證了臺架系統模型的準確性。

圖24為測試臺架負載模擬補償方法結果對比，可以看出采用本文所提出補償控制方法后的加載轉矩誤差最大值為74.27 N·m，最小值為-151.44 N·m，均值為-45.04 N·m，標準差為56.97 N·m；而補償前的加載轉矩誤差最大值為247.13 N·m，最小值為-81.72 N·m，均值為114.64 N·m，標準差為84.61 N·m。通過對比標準差可以得出補償后的加載轉矩精度提高了32.67%。試驗結果表明，本文所提出的負載模擬補償算法能有效提高功率分流混合動力系統模式切換過程的測試臺架加載精度。

圖24 加載轉矩補償效果

6 結論

（1）建立了一種包括車輛道路負載模擬動力學、模擬發動機、功率分流DHT 以及測試臺架傳動系統在內的測試臺架系統模型，其可對功率分流混合動力系統的模式切換過程進行分析及策略設計。

（2）基于臺架系統模型設計了轉速閉環跟蹤控制器，同時設計了轉速前饋校正補償器以提高轉速閉環跟蹤的抗干擾能力，并結合轉矩前饋校正補償器減小了測試臺架與實際車輛道路行駛阻力矩的動態誤差。

（3）對臺架系統模型以及負載模擬補償方法進行了仿真和試驗驗證，結果表明，臺架系統模型可準確模擬功率分流混合動力系統模式切換過程各動力源的動態性能。同時，基于臺架系統模型開發的負載模擬補償控制方法可提高加載精度32.67%以上，能夠大幅提高功率分流混合動力系統模式切換性能測試以及負載模擬的準確性。

后續將基于測試臺架系統模型對轉矩前饋校正補償器的動態調節增益進行優化，以進一步提高功率分流混合動力系統模式切換性能測試臺架的負載模擬加載精度。