面向智能車輛的路面附著系數分段識別方法*

張新榮，王 鑫，宮新樂，黃 晉，黃 丹，王鵬興

（1.長安大學，道路施工技術與裝備教育部重點實驗室，西安 710064；2.清華大學車輛與運載學院，北京 100084；3.長安大學運輸工程學院，西安 710064）

前言

近年來，隨著線控底盤技術的迅速發展，主動安全控制技術在智能汽車上得到廣泛的應用。路面附著系數作為描述路面和輪胎相互作用的重要參數，對提高控制質量有著十分重要的意義。低成本、高精度和快速收斂的識別方法一直是汽車主動控制領域的重點［1-5］。快速準確地識別路面附著系數對減少輪胎磨損、提高車輛穩定性有重要作用，對提高車輛駕駛安全性、減少事故發生有重要意義［6-10］。

國內外學者針對路面附著系數的辨識展開了廣泛研究。目前常用的方法主要分為基于實驗（experiment-based）和基于模型（model-based）兩類［11-13］。基于實驗的識別方法主要是通過傳感器直接測量和附著系數的相關信息（如輪胎變形、輪胎噪聲和路面紋理特征等）。Erdogan 等［14］在輪胎內部放置壓電傳感器，利用壓電傳感器測量出輪胎的橫向撓度，估計出路面附著系數。Roychowdhury 等［15］使用卷積神經網絡對路面進行識別，首先將路面分類為干/濕瀝青、干/濕水泥、雪和冰，然后運用卷積層對路面進行特征提取，最后通過訓練完成了道路的分類和識別。然而，基于壓電傳感器的路面識別方法需要在輪胎內部安裝傳感器，安裝維護較為困難，增加了使用成本；基于機器視覺的識別方法容易受到光照和天氣的影響，辨識的可靠性受到影響。

基于模型的識別方法是建立簡化的汽車動力學模型和輪胎模型，再利用不同的算法識別路面附著系數。該方法具有成本低和可靠性高的優點，學者們對此進行了大量研究，主要可以分為3類。第1類是基于μ-s曲線斜率的路面附著系數估計方法。Gustafsson等［16］提出了一種基于μ-s曲線斜率的路面附著系數估計方法，在達到路面附著系數前，輪胎的利用附著系數和滑移率呈線性關系，根據擬合出線性區域內的斜率來進行路面附著系數的辨識。第2類是采用智能算法的路面附著系數估計。Sadeghi等［17］利用多層感知器神經網絡對路面附著系數進行識別，神經網絡模型的輸入是與路面附著系數密切相關的動力學參數，輸出是路面附著系數。第3 類是基于Dugoff［18-19］、Hsri［20］、MF［21］和 Uni-tyre［22］模型的方法。首先對輪胎進行歸一化處理，并將路面附著系數從輪胎模型中分離出來，然后將歸一化后的輪胎力代入車輛3 自由度模型中，最后結合狀態觀測器實現路面附著系數的實時觀測。Wang 等［23］采用了強跟蹤無跡卡爾曼濾波與交互式多模型無跡卡爾曼濾波器相結合的方法實現了路面附著系數的估計。Chen 等［24］采用了自適應平方根卡爾曼濾波方法實現了路面附著系數的估計。

基于μ-s曲線斜率的識別方法只能在線性區域內進行識別。基于智能算法的估計方法，不需要車輛的準確模型和參數，但是當車輛處于復雜路況中，智能識別算法的可靠性受到影響。而基于Dugoff等模型的識別方法需要測得的參數較多，例如輪胎的側偏剛度，側偏剛度的獲取較為困難，且側偏剛度會受到輪胎垂向力和側偏特性的影響，進行實車應用的難度較大。

為應對這些問題，將路面附著系數的估計分為線性區域和非線性區域，所提算法的輸入參數有滑移率和利用附著系數。為驗證算法的有效性，本文中首先建立了車輛動力學模型。其次，采用擴張狀態觀測器的方法對利用附著系數進行估計，提高了對利用附著系數估算的準確性。提出了一種基于自適應卡爾曼濾波的車速估計算法，對噪聲特性具有較好的自適應性，估計的車速也更加準確，結合傳感器測得的輪速實現了滑移率的估計。最后通過仿真和實驗驗證了所提方法的有效性，路面附著系數的估計誤差在0.05 以內，結合路面的變化特性引入評價指標后，算法的運行效率提高了21.1%。

1 車輛動力學建模

采用車輛的3 自由度動力學模型來描述運動情況，3 自由度中包括橫擺、橫向和縱向運動。3 自由度模型如圖1所示。

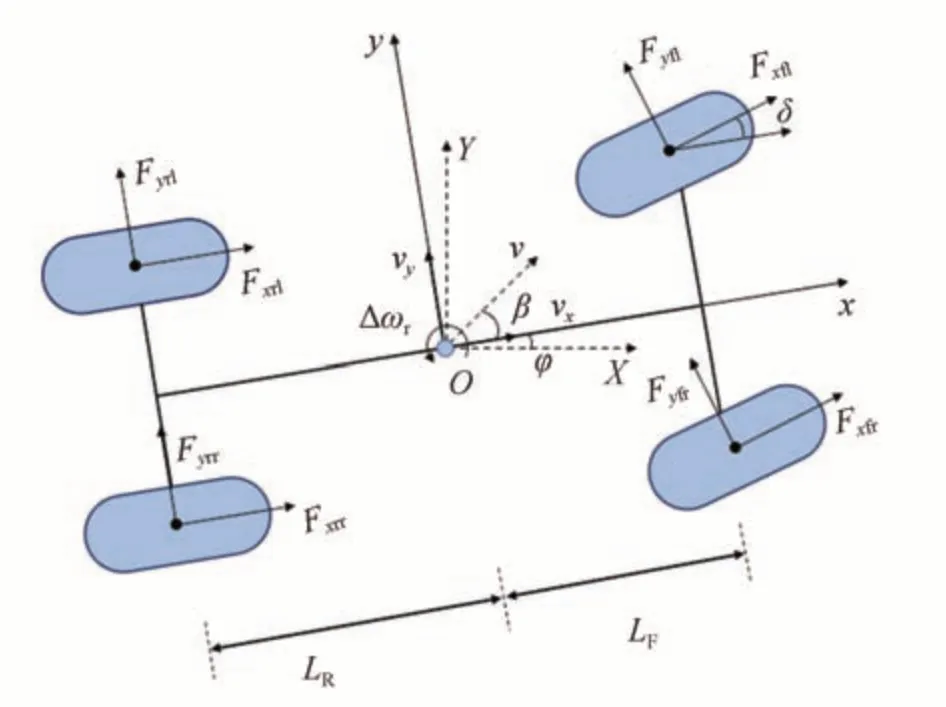
圖1 3自由度車輛動力學模型

車輛3自由度模型的動力學方程為

式中：fl、fr、rl、rr 分別代表左前輪、右前輪、左后輪和右后輪；ax、ay和ωr分別代表質心處的縱向加速度、橫向加速度和橫擺角速度；δ代表前輪轉角；m代表總質量；IZ代表繞質心處的轉動慣量；BF代表前輪之間的輪距；BR代表后輪之間的輪距；LF代表前軸到質心處的距離；LR代表后軸到質心處的距離。

4個輪胎的垂直載荷計算公式為

式中：g為重力加速度；h為質心高度。

車輪的受力分析圖如圖2所示。

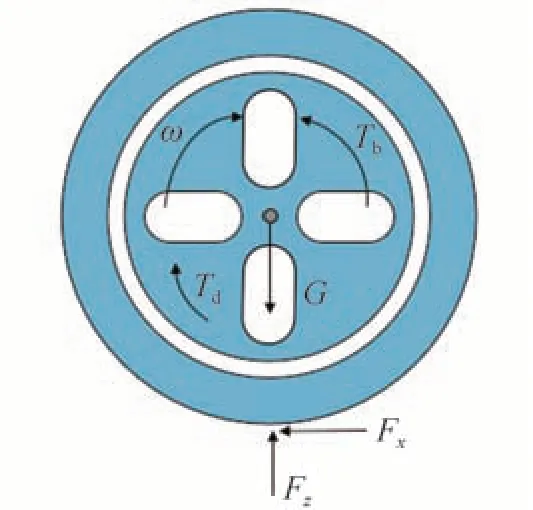
圖2 車輪模型

可以得到車輪的受力方程為

式中：i=fl，fr，rl，rr；Iw代表輪胎的轉動慣量；r代表輪胎半徑；代表角加速度；Fxi代表輪胎的縱向載荷；Tbi代表制動力矩；Tdi代表驅動力矩；Rxi代表滾動阻力矩。

輪胎的滑移率可以被定義為

式中ωi為輪胎角速度。

2 利用附著系數與滑移率的估計

為實現利用附著系數和滑移率的估算，分別采用擴張狀態觀測器對利用附著系數進行估計和自適應卡爾曼濾波對滑移率進行估計。

2.1 基于擴張狀態觀測器的利用附著系數估計

利用附著系數的定義為

式中μi為輪胎的利用附著系數。

本文主要討論制動工況下的路面附著系數估計，驅動力Tdi=0，將式（5）代入式（3）中可以得到

采用擴張狀態觀測器進行利用附著系數的估計，典型1階系統的非線性狀態空間可表示為

非線性系統須滿足如下兩個條件：

（1）f(x1，t)有界，但不要求其連續性；

（2）b(t)可以確定。

定義系統的非線性環節f(x1，t)為擴張狀態變量x2，原非線性系統可以擴張為新的線性系統：

通過式（9）可以得到1 階擴張狀態觀測器的典型形式：

式中：z1和z2分別為狀態變量x1和x2的估計值；e1為x1的估計誤差；β1和β2為觀測器的可調增益；a1和a2為濾波因子；δ為坐標原點附近的線性區間；fal函數為一種非線性反饋結構。

根據非線性誤差反饋原則，選取非線性函數fal為

通過對式（9）進行改寫，可以寫成離散形式的表達式：

式中Δt為采樣時間的間隔。

把制動力矩Tb看作系統的輸入，將含縱向力Fxfl的項視作擴張狀態變量，可定義式（12）：

由式（12）可以知曉，車輛在行駛過程中滿足f(x1，t)有界的條件，且b(t)由輪胎的轉動慣量確定，均滿足擴張狀態器設計的條件。

根據式（11）得到擴張狀態變量x2的觀測值，將其代入式（12）中便可以得知利用附著系數的估計值為

2.2 基于自適應卡爾曼濾波的滑移率估計

為實現滑移率的估計，采用基于自適應卡爾曼濾波的車速估計算法，結合傳感器測得的輪速實現了滑移率的實時估計。

在車輛轉向過程中，為得到縱向車速，須將四輪輪速求得的車速換算成后軸中心，換算的過程如式（14）所示：

式中vi代表通過輪速換算到后軸中心求得的縱向車速。

由于在制動過程中，四輪都出現明顯打滑現象，這時四輪輪速偏離實際車速，須求得四輪的最大輪速。最大輪速vbest為

算法1是車速估計的偽代碼：

基于自適應卡爾曼濾波算法的系統狀態空間模型為

式中：vk為k時刻的速度；ak為k時刻的加速度；△ak為k時刻加速度的變化量。

系統的噪聲向量為

車輛加速度的變化不是一個定值，假設其方差為δ2，故系統的噪聲協方差矩陣為

系統的量測方程為

式中rk為k時刻的量測噪聲。

由于系統噪聲特性隨著路況不同而不同，如果采用卡爾曼濾波進行處理會造成一定的偏差。采用自適應卡爾曼濾波可以對噪聲進行更新，首先須將系統狀態空間方程進行離散化：

為對過程噪聲和測量噪聲進行實時更新，須引入中間變量：

式中：Vk為殘差；Zk為k時刻的觀測值；H為觀測矩陣；rk-1為k-1 時刻觀測噪聲的均值；dk為加權系數；b為遺忘因子。

自適應卡爾曼濾波的更新方程為

式中：Kk為增益矩陣；Rk-1為觀測噪聲在k-1 時刻的協方差矩陣；I為單位矩陣。

Qk、qk、rk和Rk的更新方程為

在運用自適應卡爾曼濾波估計算法得到車速最優估計值以后，再將其代入式（4）中，從而得到輪胎滑移率的估計值。

3 路面附著系數辨識

輪胎在不同附著系數的路面上，可以獲得不同的μ-s曲線圖。隨著滑移率的變化，利用附著系數先增大后減小，一般把最大利用附著系數叫做路面附著系數。μ-s曲線如圖3所示。

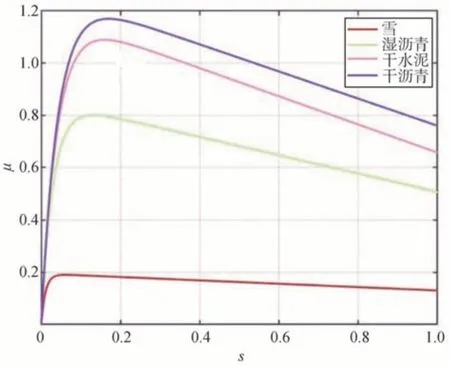
圖3 μ-s曲線圖

圖3中所示的是4條典型路面的曲線，是一種半經驗的輪胎數學模型，該模型的表達式為

輪胎模型中典型路面參數值如表1所示。

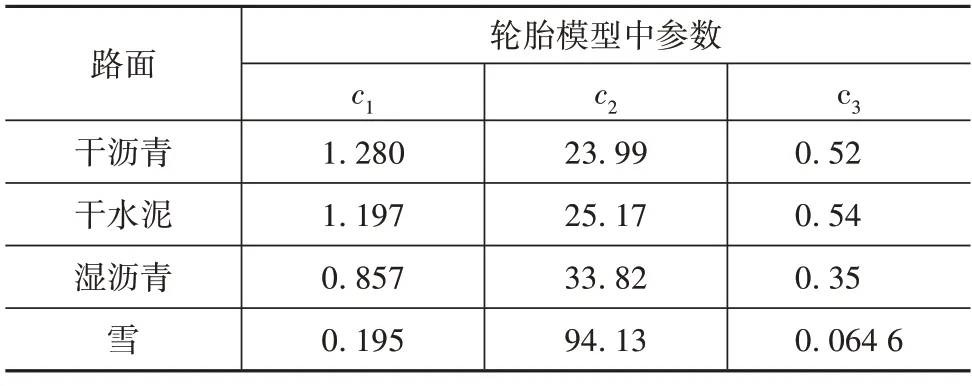
表1 模型參數

在線性區域內，通過辨識μ-s曲線斜率進行路面附著系數辨識，在非線性區域內提出了一種快速的路面附著系數辨識算法。

3.1 線性范圍內的路面附著系數辨識算法

在線性范圍內，μ和s近似為線性關系，通過擬合曲線斜率近似估計路面的附著系數。在線性范圍時，可以得到如下公式：

式中K為待辨識斜率。

采用迭代的最小二乘法進行辨識，計算公式為

式中：系統輸出的觀測信息為yt=Fz，系統輸入的觀測信息為φT=sFx，待辨識的參數θ(t)=K。

遞推最小二乘法的計算步驟為

（1）初始化參數θ(0)、P(0)及遺忘因子λ；

（2）測量系統輸出yt，計算回歸矩陣φT；

（3）計算估計誤差：e(t)=y(t)-φTθ(t-1)；

（4）計算增益矩陣：

（5）協方差矩陣：

（6）更新估計參數向量：

θ(t)=θ(t-1)+K(t)e(t)

（7）重復步驟（2）～步驟（6）。

3.2 非線性范圍內的路面附著系數辨識算法

依據μ-s曲線的特性，非線性區域內路面附著系數識別方法的原理如圖4所示。

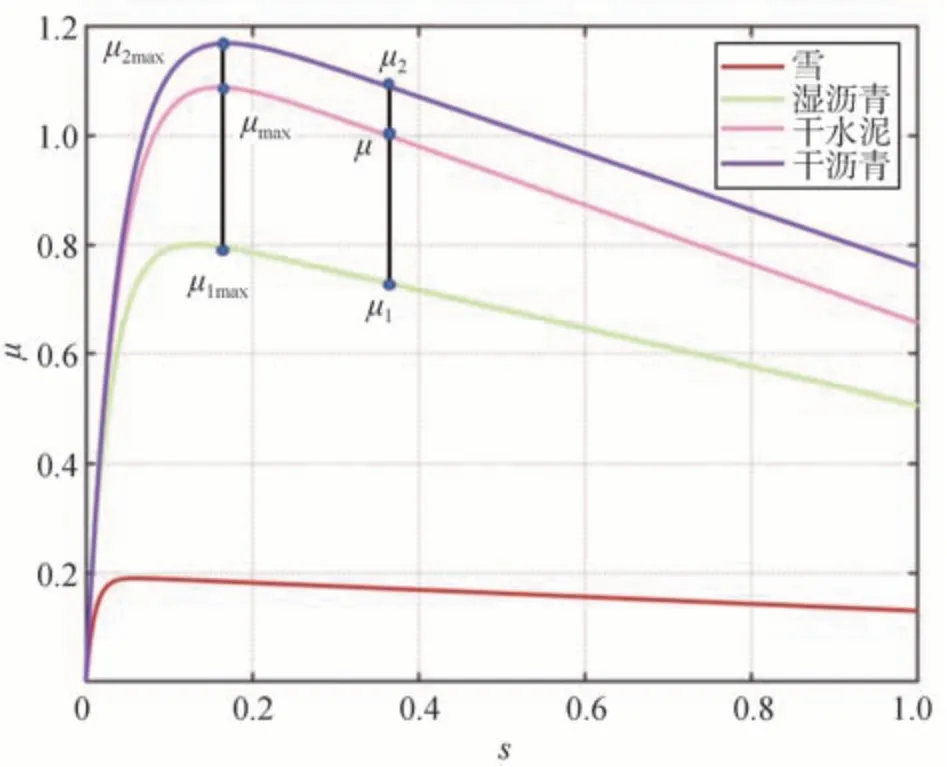
圖4 路面附著系數識別原理圖

假設干水泥的μ-s曲線未知，可以通過式（4）求出在干水泥路面某一時刻下的滑移率s，再通過式（13）求出該時刻下的利用附著系數μ。濕瀝青、干瀝青和雪路面的曲線已知，其在滑移率s下對應的利用附著系數分別為μ1、μ2和μ3。通過對比可以得知μ3＜μ1＜μ＜μ2。由此可以得知與干水泥路面附著系數最接近的兩條路面為干瀝青和濕瀝青路面。

干水泥的路面附著系數可以通過式（27）得到：

式中μ1max、μ2max和μmax分別代表濕瀝青路面、干瀝青路面和干水泥路面的路面附著系數。

在選取最相近路面的方法都須從附著系數最低的路面開始查找，直到μ滿足μ1＜μ＜μ2時停止查找。每得到一個利用附著系數都須查找一次，隨著路面數據集的增多，查找所需要的時間也就越多。在實際行駛過程中，路面的附著系數變化不會特別劇烈，重復的查找數據集會增加算法的復雜度。而在車輛緊急制動時，需要在很短的時間內得到路面附著系數情況。所以在第一次搜索到路面附著系數后都可以按照式（27）進行擬合，但是為防止路面附著系數突變，引入了以下的評價指標：

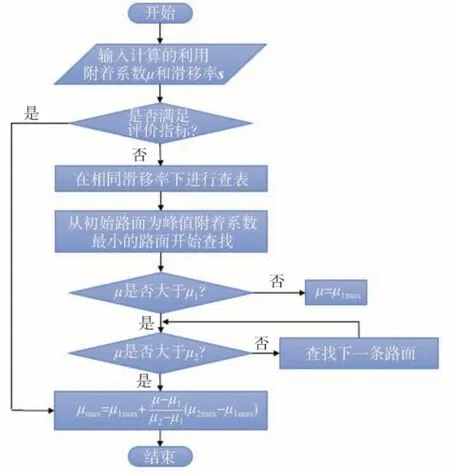
圖5 搜索算法流程圖

4 仿真與實車驗證

首先，根據實車參數設置Carsim整車仿真參數。然后采用Matlab-Carsim 聯合仿真的方法測試了算法的可行性。最后，通過實驗驗證了所提方法的有效性。

4.1 仿真驗證

仿真所采用的車輛型號是Large European Van，仿真模型如圖6所示。

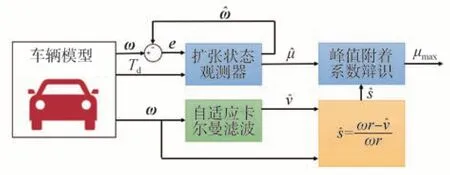
圖6 聯合仿真圖

仿真參數如表2 所示。仿真所采用的工況是車輛制動時的工況，車輛的初始速度是60 km/h，仿真采樣時間設置為0.01 s，所加的輪缸制動壓力如圖7所示。

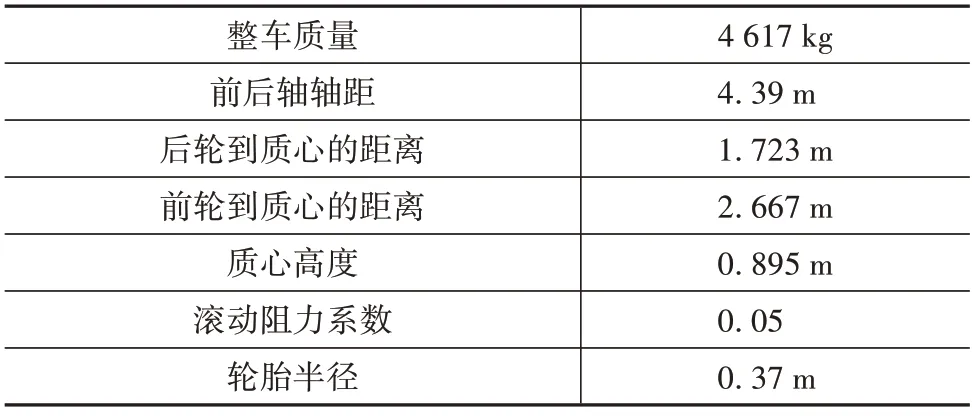
表2 參數設置表

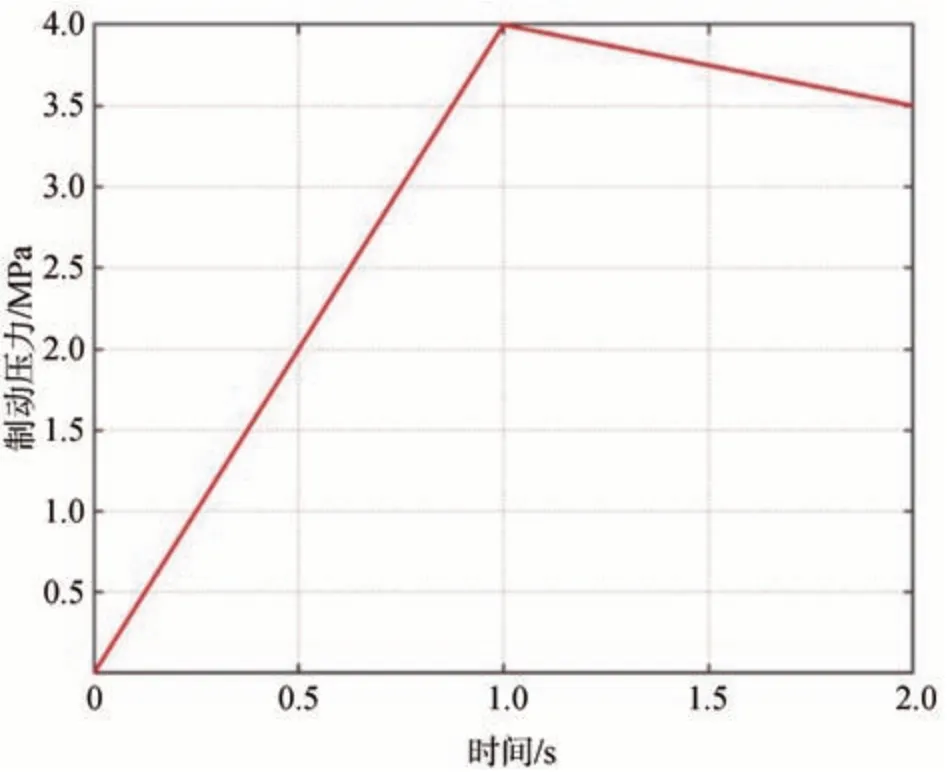
圖7 制動輪缸壓力圖

為驗證擴張狀態觀測器的優勢，分別采用兩種方法進行對比驗證。第一種方法是基于擴張狀態觀測器的方法求解得到的利用附著系數。第二種方法采用的是常規方法，通過對輪胎的角速度微分得到輪胎的角加速度，然后代入式（3）求解得到。仿真結果對比如圖8所示。

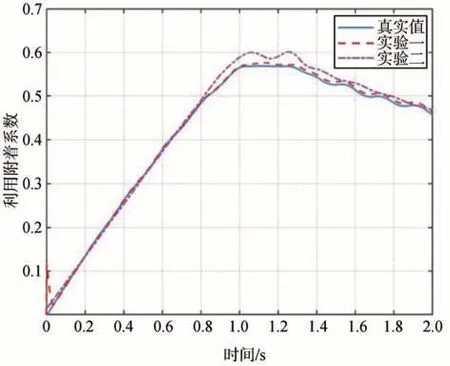
圖8 利用附著系數觀測曲線圖

通過對比發現，經過擴張狀態觀測器估計得到的利用附著系數更加接近真值，驗證了基于擴張狀態觀測器的方法在利用附著系數估計方面的優勢。

為驗證自適應卡爾曼濾波（AKF）相較于卡爾曼濾波（KF）在車速估計方面的優勢，首先對車速添加了均值和方差均為0.5 的高斯噪聲。卡爾曼濾波過程噪聲的方差Q1設置為［0，0；0，0.01］，量測噪聲的方差R1設置為0.1。自適應卡爾曼濾波過程噪聲的方差Q2的初值設置為［0，0；0，0.01］，過程噪聲的均值q2的初值設置為［0；0.01］，量測噪聲的方差R2的初值設置為0.1，量測噪聲的均值的初值設置為0.01，遺忘因子b設置為0.995。得到的車速估計結果如圖9所示。

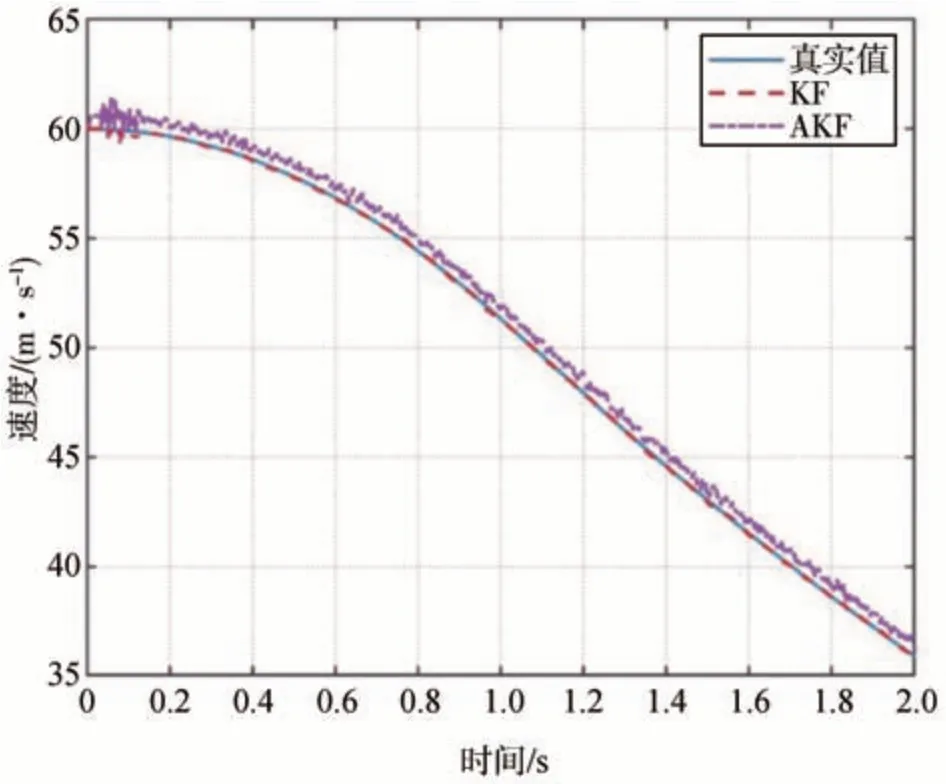
圖9 車速估計曲線圖

自適應卡爾曼濾波由于對噪聲的特性具有自適應性，對噪聲的處理效果更好，估計的車速值也更加準確。將傳感器測得的輪速值和自適應卡爾曼濾波求解得到的車速值代入式（4）中，便可以求解得到輪胎滑移率。

首先辨識的路面是均一路面，識別的路面附著系數是0.6，在0.55 s 辨識出了路面附著系數在0.6左右，辨識結果如圖10所示。

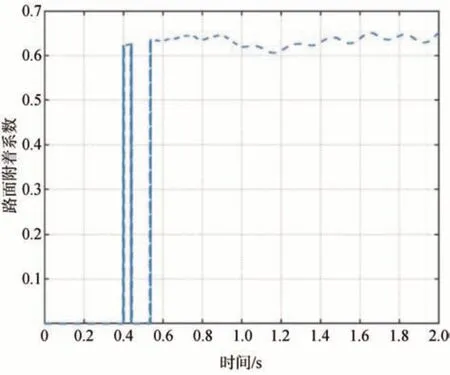
圖10 均一路面估計曲線圖

然后辨識對接路面，第一段路面是附著系數為0.4 的路面，第二段路面是附著系數為0.6 的路面。路面的辨識結果如圖11所示。

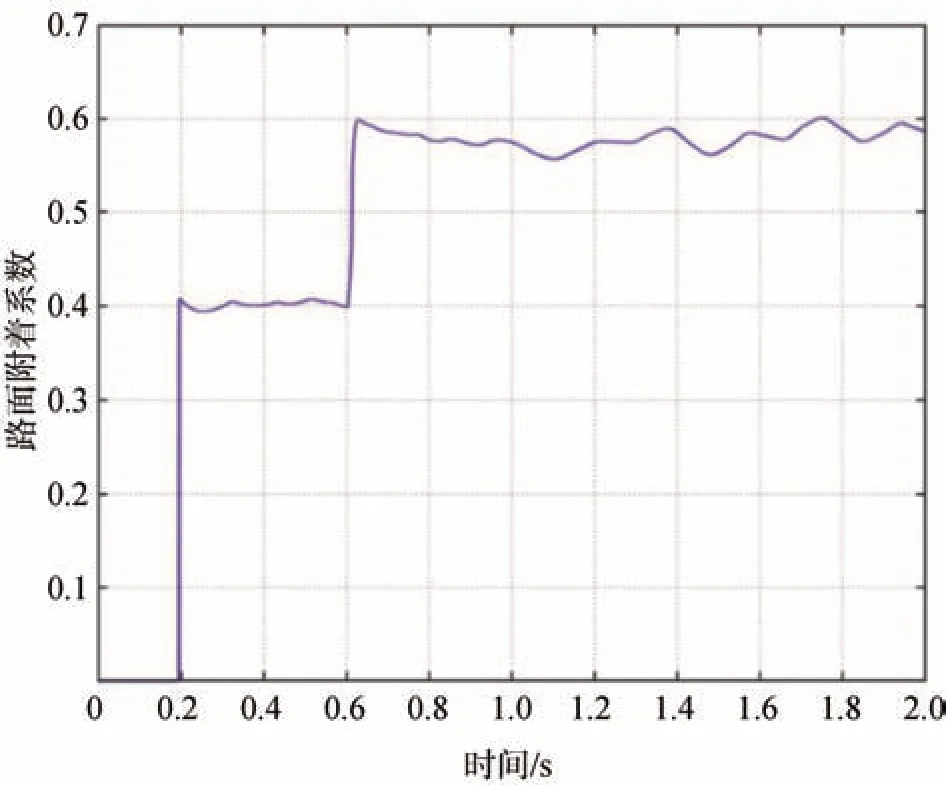
圖11 對接路面估計曲線圖

從圖中可以看到：在0.2 s時辨識出了路面的附著系數在0.4 左右；在0.6 s 時路面辨識結果有一個躍變，辨別出了路面附著系數在0.6左右。

通過對比發現，加入評價指標后，程序的運行時間縮短了0.39 s，運行效率提高了21.1%，證明了所提算法的可行性。仿真程序運行時間如表3所示。

表3 仿真程序運行時間

4.2 實車驗證

實驗車輛為自主研發的新型大客車，測試路面為瀝青路面。所用到的傳感器有IMU、輪缸壓力傳感器和輪胎角速度傳感器，都是通過總線把采集到的信息發送到上位機，傳感器的采樣時間為0.01 s。圖12展示了實驗原理圖。

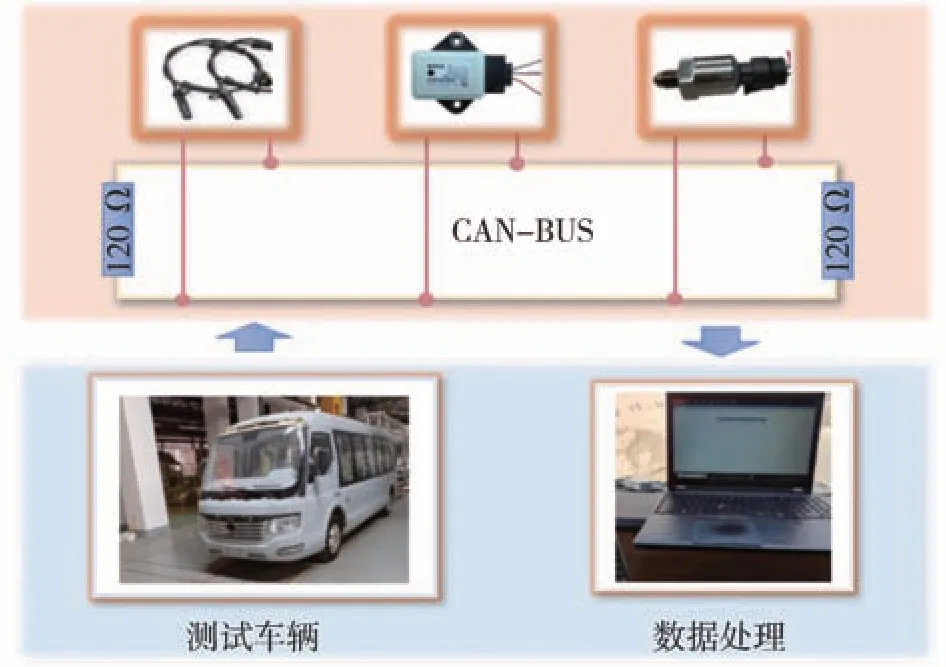
圖12 實驗原理圖

將所提算法應用到車輛的制動過程中，測試路面為瀝青路面，輪缸壓力曲線如圖13 所示。加速度曲線如圖14所示。

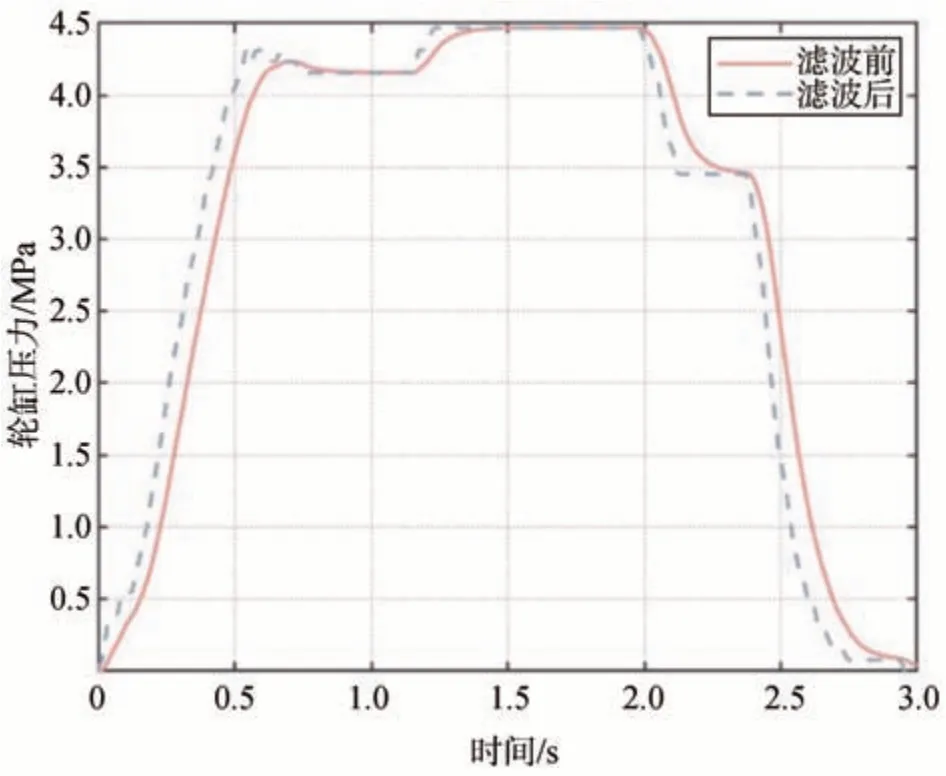
圖13 輪缸壓力曲線圖

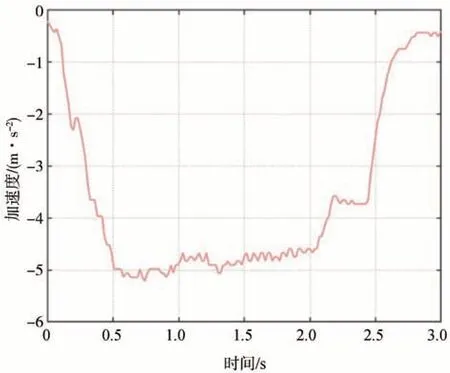
圖14 加速度曲線圖

車速估計曲線如圖15所示，圖15所示的輪速是由傳感器測得的輪速乘以輪胎半徑求得的。

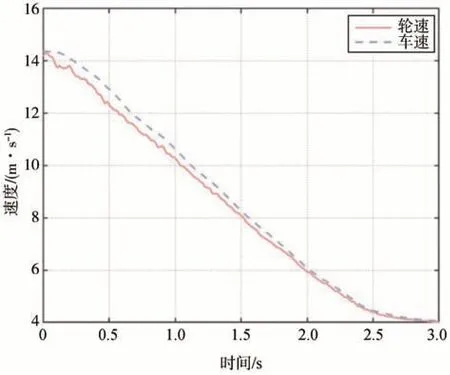
圖15 車速估計曲線圖

路面附著系數估計結果如圖16 所示。從圖16可以看出，估計的實驗結果誤差在0.05 以內，能夠滿足防抱死制動系統、牽引力控制系統和主動橫擺力偶矩控制等控制系統任務的要求。

圖16 路面附著系數估計曲線圖

5 結論

（1）采用擴張狀態觀測器的方法實現了對利用附著系數的估計。結果表明，該方法求解的利用附著系數能夠迅速收斂，相比于對輪胎角速度微分的求解方法，求解出的利用附著系數有著更高的精度。

（2）采用自適應卡爾曼濾波算法實現了車速估計。自適應卡爾曼濾波算法相比于卡爾曼濾波的車速估計方法具有更好的自適應性，估計的滑移率也更加準確。

（3）提出了一種路面附著系數分段估計方法，可以實現路面附著系數的快速和準確辨識。通過實驗驗證，所提方法的誤差在0.05 以內，可以滿足控制任務的要求。根據路面的變化特性引入評價指標，算法的運行效率提高了21.1%。