換流變壓器有載分接開關級間短路故障差動保護動作特性

閆晨光 張 芃 徐 雅 武炬臻 李凌南

（1.電力設備電氣絕緣國家重點實驗室（西安交通大學） 西安 710049 2.國網(wǎng)經(jīng)濟技術研究院有限公司 北京 102209）

0 引言

有載分接開關（On-Load Tap Changer, OLTC）是換流變壓器實現(xiàn)電壓和功率調(diào)節(jié)功能的重要控制設備，在補償交流電壓波動、穩(wěn)定直流電壓等方面具有不可替代的作用[1]。近年來，部分高壓直流換流站內(nèi)換流變壓器OLTC 在運行中突發(fā)級間短路故障，進而引起爆炸起火事故，嚴重威脅電力系統(tǒng)穩(wěn)定運行[2-3]。由于OLTC 油室狹小、內(nèi)部心體結構緊密，當發(fā)生低阻抗短路時，故障能量急劇釋放將劇烈汽化分解絕緣油并導致油壓驟升，一旦壓力水平超過油室承壓極限，OLTC 開裂爆炸將難以避免。

相比于常規(guī)電力變壓器，換流變壓器二次側連接換流裝置，其通斷過程會導致網(wǎng)、閥側端電流波形明顯畸變[4-5]。同時，換流變壓器OLTC 切換操作更為頻繁，并且切換電流變化率大，切換過程恢復電壓高，因而具有更高的故障概率和失效風險[6]。換流變壓器OLTC 級間短路一般表現(xiàn)為油室中低阻抗電弧短接相鄰兩級導體，并經(jīng)引線短接調(diào)壓繞組兩級，因此級間短路故障本質是短接繞組固定小匝數(shù)（1.25%或0.86%匝）的短路故障。此外，OLTC狹小油室和緊密機構將進一步加速故障發(fā)展，進而對繼電保護裝置的動作性能提出了更高的要求。

與交流系統(tǒng)中的常規(guī)電力變壓器類似，換流變壓器亦采用縱差動保護作為其電氣量主保護[7-8]。作為差動保護動作特性分析的理論基礎和重要前提，變壓器內(nèi)部繞組短路故障理論建模與仿真計算長期以來是業(yè)界研究的熱點問題。文獻[9]根據(jù)變壓器銘牌參數(shù)，提出了短路電抗或漏電感矩陣線性拆分的自互感模型。這種方法計算效率高且大大簡化繞組短路故障模型，因此被廣泛應用于變壓器內(nèi)部短路故障分析與繼電保護研究[10-12]。文獻[13]通過解析計算建立了電力變壓器內(nèi)部各種短路故障下短路電抗的定量表達式，明確了短路電抗隨故障位置變化存在的非線性關系。文獻[14]基于時域場路耦合電磁模型分析了變壓器繞組匝間短路條件下電流、磁通以及繞組受力的諧響應，并開展動模試驗驗證了方法的正確性與有效性。

在故障特征研究的基礎上，一些學者進一步分析和討論了不同條件下變壓器差動保護的動作特性。文獻[15-16]提出了電力變壓器內(nèi)部短路故障電路模型和分析方法，并根據(jù)仿真結果分析了現(xiàn)有差動保護的靈敏性問題。文獻[17]建立了特高壓變壓器的動態(tài)仿真模型，分析比較了不同故障情況下各類差動保護的靈敏性。文獻[18]研究了換流器非線性特征對換流變壓器差動保護的影響，并分析了三種典型故障場景下保護的動作特性。文獻[19]針對變壓器差動保護采用的各種比率制動方式進行了對比分析，研究了區(qū)內(nèi)故障時不同制動方式差動保護的靈敏性和安全性。上述研究成果為分析換流變壓器OLTC 級間短路故障下差動保護的動作特性提供了有益借鑒。

目前，換流變壓器OLTC 級間短路故障已經(jīng)引起業(yè)界高度關注，現(xiàn)有錄波數(shù)據(jù)表明差動保護在故障過程中存在靈敏性、速動性不足的問題。但是，由于缺少有效的理論模型及仿真手段，級間短路故障特征尚不明晰，針對差動保護動作特性的定量分析亦難以深入。基于此，本文從換流變壓器OLTC典型過渡電路拓撲入手，分析OLTC 油中電弧引起級間短路的故障過程，建立含油中電弧時變電導特性的直接場-路耦合模型，仿真分析OLTC 不同分接位置短路故障下常用差動保護方案的動作性能。

1 OLTC 級間短路故障分析

作為換流變壓器內(nèi)部唯一常動部件，OLTC 通常承受著更為復雜的機械和電氣應力。隨著調(diào)壓次數(shù)的增多，其不良操作和失效概率也相應增加[20-22]。級間短路故障是OLTC 電氣故障的主要形式，其故障回路由OLTC 油室內(nèi)部相鄰兩級間高能電弧、調(diào)壓引線以及調(diào)壓繞組故障段構成，如圖1 所示。

圖1 換流變壓器OLTC 級間短路故障示意圖Fig.1 Schematic diagram of a converter transformer intertap short-circuit fault inside the OLTC

圖2 給出一種典型真空OLTC 過渡電路拓撲[23]和級間短路故障回路。多起換流變壓器事故表明，級間短路故障通常發(fā)生在OLTC 切換操作完成后。在OLTC 正常切換時，主通斷觸頭與過渡通斷觸頭在真空泡中開斷電流，有效地避免了油中拉弧引起的絕緣油碳化[24]。但是，OLTC 長期的帶載切換存在觸頭磨損、機構卡澀、彈簧失能等風險，真空泡亦可能出現(xiàn)真空泄漏、波紋管損壞等問題。這都將導致OLTC 切換過程中轉換開關被迫在油中帶電拉弧。某次切換操作完成后，主轉換開關相鄰兩級間突發(fā)低阻抗電弧放電，從而形成一條不經(jīng)過過渡電阻的短路故障回路。短路環(huán)流isc產(chǎn)生的巨大焦耳熱將造成金屬觸頭嚴重熔蝕和絕緣油劇烈汽化分解，最終導致切換心體損壞和OLTC 油室破裂爆炸。

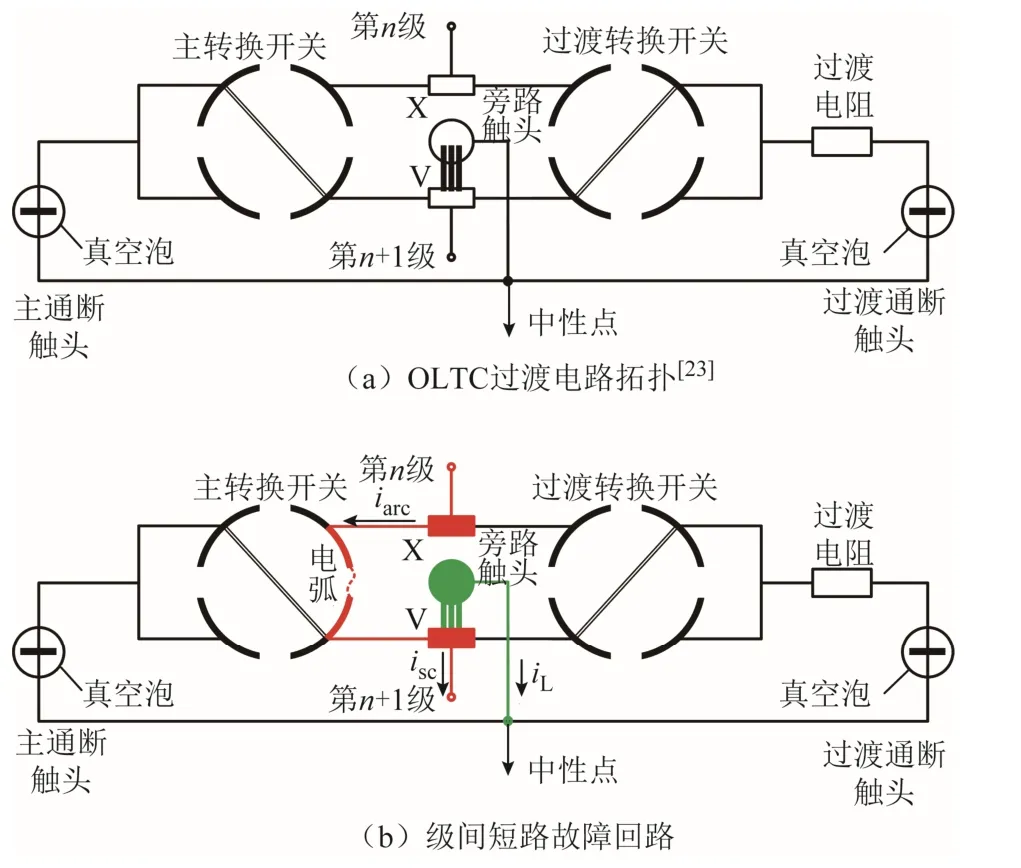
圖2 OLTC 過渡電路拓撲和級間短路故障回路Fig.2 Circuit topology and intertap fault loop of OLTC

2 數(shù)學模型

換流變壓器發(fā)生OLTC 級間短路故障時，巨大短路電流流過調(diào)壓繞組故障段，引起內(nèi)部漏磁分布顯著畸變，進而造成繞組漏感參數(shù)發(fā)生變化。在OLTC 油室內(nèi)部，高能電弧短接相鄰兩級導體，其時變電導特性將顯著影響短路電流。因此，OLTC 級間短路故障是一個復雜的場-路耦合物理問題，涉及繞組漏磁分布、外部電路拓撲以及故障點處油中電弧時變電導的相互作用。基于此，本章依次建立換流變壓器內(nèi)部電磁場方程、外部電路方程以及電弧電導微分方程，進而提出OLTC 級間短路故障直接場-路耦合模型。

2.1 電磁場-電路聯(lián)合方程

基于Maxwell 方程組，換流變壓器內(nèi)部電磁場可用偏微分方程描述[25]為

式中，ν為介質的磁阻率；A為空間磁矢位；Js為空間電流密度矢量；σ為介質的電導率；t為時間。

在計算換流變壓器內(nèi)部磁通分布時，一般認為繞組為鉸鏈導體而不考慮其中的渦流場[26]。此時適用于換流變壓器繞組的三維電磁場方程可表示為[27]

式中，Js為電流密度矢量，有

式中，N為繞組中細導線總數(shù)；Is為流入繞組的總電流；Ssc為繞組的總截面積。

對于外部電路，模型的輸入電壓Ui為繞組感應電壓與外部電阻和電感上的總壓降之和[26]，即

式中，V為三維電磁場求解域；R為繞組直流電阻及外部電路總電阻之和；L為外部電路的總電感。

聯(lián)合式（2）～式（4），電磁場-電路統(tǒng)一矩陣方程為

式中，K和P均為系數(shù)矩陣，由式（2）和式（3）中換流變壓器繞組相關幾何參數(shù)和材料屬性決定。

2.2 電弧電導微分方程

不同于常規(guī)電力變壓器繞組匝間、接地短路故障，換流變壓器OLTC 級間短路故障回路不僅包含低阻抗故障電弧，還包含OLTC 內(nèi)部觸頭和導體、調(diào)壓引線以及調(diào)壓繞組被短路段。因此，OLTC 級間短路故障回路電阻Rsc可表示為

式中，Rc為OLTC 內(nèi)觸頭和導體電阻，在計算中可忽略不計；Rw為調(diào)壓引線電阻；garc為故障電弧的時變電導，由非線性常微分方程描述。

封閉腔體內(nèi)油中燃弧試驗[28-29]表明，高能電弧劇烈汽化絕緣油并形成脈動增長的氣泡，因此油中電弧本質上為氣體電弧。目前常用的氣體電弧黑盒模型有Cassie 模型[30]、Mayr 模型[31]、控制論模型[32]、Schavemaker 模型[33]等。經(jīng)典Cassie 和Mayr 模型對于不同時刻下電弧特性的描述準確性不同[34-35]，結合兩者優(yōu)勢的Schavemaker 模型在電流零區(qū)參數(shù)的測量和選取方面亦存在局限性。考慮到級間短路環(huán)流峰值可達數(shù)十千安，且電弧電流過零存在暫態(tài)特征，本文選取基于電弧直徑的改進電弧模型[36]模擬油中電弧的時變電導特性，通過引入隨電流變化的電弧直徑參數(shù)以實現(xiàn)對于大電流區(qū)故障環(huán)流的定量求解，以及電流零區(qū)暫態(tài)特征的準確描述。

基于電弧直徑的電弧模型方程一般形式為[36]

式中，τ為時間常數(shù)；uarc和iarc分別為電弧電壓和電弧電流；Vs為穩(wěn)定燃弧區(qū)的弧柱壓降，近似為常數(shù)；a和c均為附加校正因子；darc為隨電弧電流iarc變化的電弧直徑，可按式（8）估計。

式中，b和q為常數(shù)參數(shù)。

將式（8）代入式（7），并將Vs、a、c、b、q五個參數(shù)整理合并，得到更為簡單的電弧微分方程表達形式為

式中，sV?和β均為自由參數(shù)，其值根據(jù)油中電弧故障現(xiàn)場試驗[28-29]所得電弧電壓波形驗證選取。

2.3 直接場-路耦合關系

換流變壓器OLTC 級間短路故障直接場-路耦合關系如圖3 所示。在每一時間步長下，換流變壓器外部電路輸入電流為內(nèi)部鐵心和繞組有限元模型提供激勵，利用電磁場控制方程計算內(nèi)部磁通分布并得到耦合接口處的感應電壓；同時，電弧電壓和短路電流作為變量代入電弧電導常微分方程，求解得到電弧時變電導。隨后，將新生成的感應電壓與電弧電導帶入外部電路方程進行下一步運算。相比于場-路間接耦合法存在計算精度不足的問題，直接場-路耦合法能夠實現(xiàn)每一時刻下電磁場與電路之間的雙向數(shù)據(jù)交換，進而保證各部分模型間的瞬態(tài)同步求解。

圖3 直接場-路耦合關系Fig.3 Direct field-circuit coupling relationship

3 級間短路故障建模與仿真

3.1 直接場-路耦合建模

以±800 kV 特高壓直流換流站典型 ZZDFPZ-509400/500-400 單相兩柱旁軛式換流變壓器為研究對象，根據(jù)表1 中主要銘牌和幾何結構參數(shù)建立換流變壓器鐵心和繞組三維模型并進行網(wǎng)格剖分，如圖4 所示。模型中心柱和旁軛分別簡化為圓柱體和橢圓柱體，心柱周圍由內(nèi)而外依次布置調(diào)壓繞組、網(wǎng)側繞組和閥側繞組。網(wǎng)、閥側繞組簡化為完整同心圓筒結構，而調(diào)壓繞組簡化為14 段相同的同心圓筒結構，根據(jù)算例設置部分接入外電路。該型號換流變壓器14 段調(diào)壓繞組通過引線與OLTC 分接選擇器相連，每條調(diào)壓引線均采用長度為10 m、橫截面積為240 mm2、電阻率為0.020 97 Ω·mm2/m 的電纜。此外，三維有限元模型包含262 249 個四面體網(wǎng)格單元，按照油箱尺寸設置邊界并定義第一類邊界條件。

表1 換流變壓器主要銘牌和幾何參數(shù)Tab.1 Main nameplate and geometric parameters of the simulated converter transformer

圖4 換流變壓器鐵心和繞組三維有限元模型Fig.4 3-D finite-element model of core and windings inside the simulated converter transformer

換流變壓器外部電路為等電壓雙12 脈動雙極接線的±800 kV 特高壓直流工程送端電網(wǎng)極Ⅰ換流系統(tǒng)，如圖5 所示。極Ⅰ系統(tǒng)包含高端組和低端組兩個12 脈動換流單元，各單元由Y/Y 和Y/D 兩種接線的換流變壓器組和換流閥組構成。各換流變壓器組包含三臺單相換流變壓器，網(wǎng)側出線接入500 kV交流母線，閥側出線與六脈動換流裝置相連。

圖5 ±800 kV 特高壓直流工程送端電網(wǎng)極Ⅰ換流系統(tǒng)Fig.5 Schematic diagram of the pole Ⅰconverter system in a ±800 kV UHVDC sending-end network

基于鐵心和繞組三維有限元模型與外部電路拓撲，通過Ansys Maxwell 瞬態(tài)磁求解器與Simplorer瞬態(tài)仿真器開展級間短路故障瞬態(tài)協(xié)同仿真計算，實現(xiàn)耦合接口處的雙向數(shù)據(jù)傳輸。參數(shù)設置如下：三相交流電源電壓有效值Us=306 kV，調(diào)壓引線電阻Rw=0.874 mΩ，電弧時間常數(shù)τ=38 μs，電弧自由參數(shù)為sV?=213 V、β=1.015，換流器觸發(fā)角α=15°，平波電抗器Ld=75 mH，直流側等效電阻Rd=140 Ω。

3.2 典型故障算例

本節(jié)以A 相換流變壓器心柱2 繞組對應OLTC在t=40 ms 時突發(fā)+6/+7 級間短路故障為例，利用場-路耦合數(shù)值方法計算換流變壓器故障前后內(nèi)部磁場分布、短路電流、電弧電壓以及端電流的變化。

換流變壓器內(nèi)部磁感應強度矢量三維分布和二維橫截面磁通分布分別如圖6 和圖7 所示。圖6a、圖7a 中，正常運行時換流變壓器內(nèi)部漏磁近似為零，磁通線主要被約束在鐵心內(nèi)。t=40 ms 發(fā)生OLTC級間短路故障后，巨大短路電流在調(diào)壓繞組中部感應出峰值達3.77 T 的橫向漏磁，導致繞組整體磁通分布發(fā)生顯著畸變，如圖6b、圖7b 所示。t=55 ms時，大量磁通線密集環(huán)繞于調(diào)壓繞組故障段，附近漏磁強度峰值可達4.0 T。

圖6 換流變壓器內(nèi)部磁感應強度矢量三維分布Fig.6 3-D magnetic vector flux distributions inside the simulated converter transformer

圖7 換流變壓器內(nèi)部二維橫截面磁通分布Fig.7 2-D cross-sectional magnetic flux distribution inside the simulated converter transformer

短路電流、電弧電壓及端電流仿真波形如圖8所示。受換流閥通斷影響，端電流不再為標準正弦波形，而在每個周波內(nèi)呈現(xiàn)對稱梯形波形。t=40 ms突發(fā)級間短路后，換流變壓器內(nèi)部顯著的漏磁畸變將在故障段繞組上感應出巨大的反向電動勢，并在故障回路中產(chǎn)生峰值達92.87 kA 的短路電流，電弧持續(xù)60 ms 內(nèi)平均電弧電壓為250.66 V。此時，A相換流變壓器網(wǎng)側電流由原來的梯形平頂波形變?yōu)槿切渭忭敳ㄐ危浞逯祻?.26 kA 上升到2.21 kA。此外，由于級間短路故障引起的電壓比改變相對較小，閥側端電流并未表現(xiàn)出明顯變化。

圖8 短路電流、電弧電壓及端電流仿真波形Fig.8 Simulation waveforms of the short-circuit current,the arc voltage and the terminal currents

為進一步探究不同級間短路故障下電氣量的變化特征，在相同模型參數(shù)下對14 組不同分接位置級間短路故障開展仿真計算，得到短路電流峰值和網(wǎng)側電流峰值增量隨分接位置的變化規(guī)律，如圖9 所示。

圖9 不同分接位置故障下短路電流及端電流變化情況Fig.9 Variations of short-circuit current and line-side current under faults between different taps

結果表明，OLTC 不同分接位置級間短路故障的嚴重程度存在顯著差異。當故障發(fā)生在調(diào)壓繞組中部對應分接位置+6/+7 時，短路電流峰值達到92.87 kA，同時網(wǎng)側電流峰值增量也相應達到最大值75.40%。相對地，當下端部對應分接位置+13/+14 故障時，短路電流峰值為53.48 kA，僅為最嚴重條件下的58%。可以看到，不同分接位置短路故障電流峰值及網(wǎng)側電流峰值增量呈現(xiàn)非對稱分布特征，由于接入電路的調(diào)壓繞組段數(shù)不同，上端部+0/+1 級間短路故障相較于下端部+13/+14 更為嚴重。

4 差動保護動作特性分析

換流變壓器采用差動保護作為主保護，用于甄別繞組接地、匝間短路等內(nèi)部故障[37]。本節(jié)針對主保護中比率差動、工頻變化量比率差動及零序差動三種主要配置的保護方案進行動作特性分析。

4.1 比率差動保護

為避免外部故障等引起的誤動，微機型變壓器保護普遍采用具有比率制動特性的差動保護[38]。具有“三折線”制動特性的保護動作方程一般形式為

式中，Iop為動作電流，是端電流相量和的有效值；I0為啟動電流；Ir為制動電流，為端電流有效值的平均；Ir0、Ir1為“拐點電流”；K1、K2為制動系數(shù)。

以實際工程中兩種常用的保護裝置為例，對比率差動保護的動作特性進行分析。裝置1 動作特性參數(shù)為：I0=0.2IN，Ir0=0.25IN，Ir1=0.5IN，K1=0.2，K2=0.5；裝置2 動作特性參數(shù)為：I0=0.5IN，Ir0=2.5IN，Ir1=10IN，K1=0.2，K2=1。其中，IN表示額定電流。

基于故障仿真結果，計算差動電流和制動電流及其對應的保護門檻，如圖10 所示。t=40 ms 后，差動電流從零開始增加。由于故障導致的制動電流增長未超過2.5(pu)，裝置2 動作門檻恒保持在初始制動段。當t=57.6 ms 時，差動電流達到裝置1 比率差動保護動作門檻，但全程未達到裝置2 門檻，可見在該故障條件下裝置2 因靈敏性不足而拒動。需要指出的是，OLTC 級間短路故障瞬時差動電流不具有勵磁涌流所含二次諧波、電流間斷角等特征，實際裝置在閉鎖元件開放保護后即可動作于跳閘。

圖10 算例中端電流與比率差動電流曲線Fig.10 Curves of terminal currents and ratio differential currents in the study case

為進一步分析兩種裝置在不同分接位置級間短路故障條件下比率差動動作特性，將3.2 節(jié)中14 組算例對應正常運行和故障條件下的工作點分別繪制于兩種裝置的比率差動動作平面上，比率差動保護動作特性平面及工作點分布如圖11 所示。不同分接位置級間短路故障工作點在比率差動保護的動作特性平面上呈非對稱分布。+13/+14 短路故障下差動電流的有效值為0.23(pu)，對應于最低的故障工作點。正常運行時的工作點偏離集中分布區(qū)域，位于接近Ir坐標軸的位置。

圖11 比率差動保護動作特性平面及工作點分布Fig.11 Operating characteristic plane and operating point distribution of ratio differential protection

通過比較工作點橫坐標發(fā)現(xiàn)，與外部故障時制動電流不同，級間短路故障制動電流與正常運行時差別較小。對于拐點電流Ir0大于1(pu)的裝置2而言，其能否反映級間短路故障主要取決于初始制動段動作電流I0的選取。當I0取為0.5(pu)時，14 組級間短路故障算例下動作電流均未達到整定門檻。相比之下，裝置1 在制動電流小于1(pu)部分的動作區(qū)域更大，能夠反映+3/+4、+4/+5、+5/+6、+6/+7、+7/+8 共五組級間短路故障。但仍有其他9組故障情況落于動作區(qū)之外，此時保護將拒動。由此可見，對于換流變壓器OLTC 級間短路故障，采用常規(guī)比率制動特性的差動保護存在靈敏性不足的問題。

4.2 工頻變化量比率差動保護

由于常規(guī)比率制動式差動保護的制動電流包含正常運行時的負荷電流，發(fā)生繞組小匝數(shù)弱故障時制動電流過大將導致保護無法靈敏甄別。針對此問題，部分裝置增設工頻變化量比率差動保護[37]，采用故障增量電流作為動作量和制動量，消除負荷電流影響以提高靈敏度。工頻變化量比率差動保護中的動作量Iop和制動量Ir為

式中，ΔI1˙和ΔI2˙分別為兩側端電流工頻變化分量。

工頻變化量比率差動保護采用“兩折線”或“三折線”制動特性。其中，“三折線”型動作方程滿足式（10），其動作特性參數(shù)為：I0=0.2IN，Ir0=IN/3，Ir1=3IN，K1=0.6，K2=0.75。同時，常用“兩折線”型工頻變化量比率差動保護的動作方程為[37]

對于典型故障算例端電流仿真結果，根據(jù)式（11）計算得到工頻變化量比率差動保護動作電流、制動電流以及其對應的保護門檻，如圖12 所示。

圖12 算例中端電流與工頻變化量比率差動電流曲線Fig.12 Curves of terminal currents and fault incremental ratio differential current in the study case

圖12 中，工頻變化量比率差動電流在故障后迅速升高并超過保護門檻。與常規(guī)比率差動保護相比，故障增量動作電流明顯大于全量動作電流，且對于故障算例表現(xiàn)出更高的靈敏性。此外，動作電流在故障后5.6 ms 達到門檻，相較于比率差動保護縮短12 ms。需要指出的是，實際裝置動作還須等待二次諧波制動、間斷角閉鎖等元件開放保護。

為分析OLTC 不同分接位置級間短路故障條件下工頻變化量比率差動保護動作特性，將14 組算例對應工作點繪制于動作平面上。如圖13 所示，不同分接位置級間短路故障的工作點在動作特性平面上呈直線分布。其中，最嚴重的+5/+6 和+6/+7 級間短路故障對應的工作點位于直線最高處，+13/+14 故障對應于直線的最低點，而正常運行時的工作點位于接近坐標原點的位置。對于14 組仿真算例，其故障工作點均落于動作特性平面的動作區(qū)內(nèi)，保護正確動作。因此，采用故障增量電流作為判據(jù)的工頻變化量比率差動保護的靈敏性與全量比率差動保護相比具有顯著優(yōu)勢。

4.3 零序差動保護

除配置比率制動式差動保護外，換流變壓器還裝設零序差動保護用于保護中性點接地的網(wǎng)側繞組，其動作方程通常采用“兩折線”制動特性，即

式中，K0為制動系數(shù)，表征不同工況下保護的制動需求，一般取0.5～0.8[7]。

根據(jù)動作電流的不同，現(xiàn)有換流變壓器零序差動保護方案主要分為兩類，其保護判據(jù)選取的動作電流Iop和制動電流Ir分別可按式（14）和式（15）計算[7,39]。

式中，3I˙0.s為換流變壓器網(wǎng)側三相零序電流；3I˙0.n為網(wǎng)側中性點零序電流。

本節(jié)針對采用這兩類零序差動保護判據(jù)的兩套裝置進行討論。采用第一類判據(jù)的保護裝置動作特性參數(shù)為：I0=0.3IN，K0=0.5；采用第二類判據(jù)的保護裝置動作特性參數(shù)為：I0=0.1IN，K0=0.8。

基于3.2 節(jié)故障仿真結果，計算網(wǎng)側三相零序電流3I˙0.s以及中性點零序電流3I˙0.n，得到零序差動電流和制動電流及其對應的保護門檻如圖14 所示。級間短路故障下，雖然三臺單相換流變壓器短路電抗的不平衡使得中性點產(chǎn)生零序電流，但網(wǎng)側繞組兩端零序電流相量和恒定為零，即對于第一類判據(jù)，故障零序電流表現(xiàn)為穿越電流，對應動作電流恒定為零，保護拒動。第二類保護判據(jù)下動作電流為中性點零序電流，級間短路故障后動作電流快速上升，但全程均未達到保護門檻。

圖14 算例中端電流與零序差動電流曲線Fig.14 Curves of terminal currents and zero-sequence differential current in the study case

為分析不同分接位置級間短路故障下零序差動保護動作特性，將14 組仿真算例對應工作點繪制于兩類零序差動保護的動作平面上，如圖15 所示。

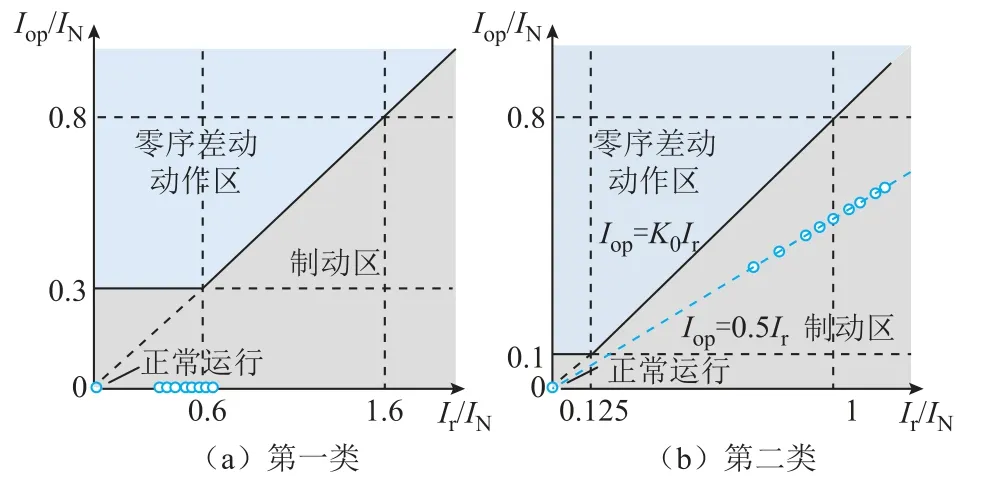
圖15 零序差動保護動作特性平面及工作點分布Fig.15 Operating characteristic plane and operating point distribution of zero-sequence differential protection

圖15a 中，不同分接位置級間短路故障下第一類動作電流均為零，其故障工作點位于Ir軸上，表明此類判據(jù)難以有效反映此類故障。對圖15b 所示的第二類零序差動保護而言，14 組算例工作點同樣均落于制動區(qū)。級間短路故障下，3I˙0.s與3I˙0.n幅值相等、相位相反，制動電流在數(shù)值上始終等于動作電流的 2 倍，所以動作平面上14 組工作點沿直線Iop=0.5Ir分布。該方案能否甄別級間短路故障主要取決于制動系數(shù)K0的選取，實際工程中為避免保護誤動通常滿足K0＞0.5，因此現(xiàn)有零序差動保護難以對OLTC 級間短路故障進行有效的判別和切除。

5 結論

近年來，國內(nèi)相繼發(fā)生的換流變壓器OLTC 級間短路故障受到各方廣泛關注，但由于缺少有效的級間短路故障模型和計算方法，目前此類故障下差動保護動作性能研究尚不充分。本文提出含電弧時變電導特性的換流變壓器OLTC 級間短路故障直接場-路耦合模型及求解算法，以±800 kV 特高壓直流換流站ZZDFPZ-509400/500-400 換流變壓器作為研究對象，開展OLTC 級間短路故障建模仿真并定量分析比率差動、工頻變化量比率差動及零序差動三種常用保護方案的動作特性。

結果表明，伴隨OLTC 級間短路故障發(fā)生，換流變壓器內(nèi)部感應出大量橫向漏磁并在短路環(huán)中產(chǎn)生嚴重故障環(huán)流。故障級位于繞組中部時，橫向漏磁和短路環(huán)流最大，其峰值分別達到3.77 T 和92.87 kA。OLTC 不同分接位置級間短路故障下，采用端電流全量作為動作量和制動量的比率制動式差動保護存在靈敏性不足的問題，尤其面對故障段靠近繞組端部的情形存在拒動風險。由于故障下零序電流表現(xiàn)為穿越電流，現(xiàn)有零序差動保護亦難以有效反映此類故障。相比之下，采用故障增量電流的工頻變化量比率差動保護對于OLTC 級間短路故障具有更高的靈敏度。