深水采油樹生產回路運維可用性分析*

龐 楠，熊中剛，劉 忠，王為慶，徐嘉宏

（桂林航天工業學院機電工程學院，廣西桂林 541004）

0 引言

深水采油樹作為水下油氣生產系統的核心設備，主要用于油氣開采、注氣注水、修井、流量控制及監測等作業[1]。采油樹直接連接油氣生產井口，一旦出現故障，會嚴重影響整套水下生產系統的工作效率。由于深海環境壓力高、洋流沖擊大、水下能見度差等多項難題，國內有相關水下檢測維修經驗的公司或院校寥寥無幾，檢測維修技術還依賴國外，但國外維修售價高、停機期長、人力成本高，大大增加了我國深水油氣開發項目的成本和周期，并隨時有被國外大廠“卡脖子”的風險，嚴重威脅了我國能源戰略安全和國民經濟發展[2-3]。因此，在采油樹投入生產前，需要對其進行嚴格的可靠性設計和預防性維修，并在采油樹運維過程中進行實時可靠性狀態評估，這對水下油氣的安全生產至關重要。

有研究表明[4-5]：深水采油樹故障率達到206×10-6，僅次于水下控制系統，失效率是其他核心設備的2.9～18.5 倍。鑒于此，很多學者對采油樹關鍵部件的可靠性開展了相關研究。針對井口連接器方面，Buitrago 等[6]采用傳統累積損傷法，根據S-N 曲線定義的局部應力和疲勞抗力計算了井口連接器疲勞壽命。Wang 等[7]在缺乏失效數據情況下，提出了一種將有限元分析與動態貝葉斯模型相結合的疲勞裂紋材料老化故障診斷方法，進行了井口連接器的可靠性分析，得出在出現裂縫的情況下，水下連接器在使用30年后結構失效概率從0.022 8增加到0.207 5；同時，采用蒙特卡羅仿真和基于DBN 的可靠性分析方法，得到在材料強度老化情況下，連接器驅動環結構可靠度達到96.26%的結論[8]；結合赫茲接觸理論對油管懸掛器密封性能進行了研究，證明了c 形密封圈在0.1～0.375 mm 干涉范圍內具有優良的密封性能和結構完整性[9]。

針對控制系統方面，Liu等[10]提出了一種混合多階段控制系統規則約束預測方法，解決了采油樹控制系統壽命預測過程中不確定性、難以獲得實時觀測數據以及數據采集噪聲影響等問題。岳明陽等[11]基于貝葉斯-GO 法對采油樹控制系統進行可靠性分析，得到水下控制模塊和生產翼閥失效率最高，失效概率分別達0.023 54 和0.019 543，并建議早期維護須注重對這2個部位進行檢測。Liu等[12]提出一種電氣控制系統組件的雙因素退化模型，建議地面控制系統在連續工作7 000 h 后停機維護，可提高系統可靠性。

另外，Guo 等[13]提出了一種由管理和多個系統代理組成的采油樹可靠性建模流程，發現生產節流閥、管線、采油樹帽和化學控制閥對系統可靠性影響較大。Hamilton-Smith[14]分析了第三方載荷對采油樹框架結構的影響，將關鍵位置的位移和結果應變值與允許限值進行比較，以確保符合設計要求。Liu等[15]提出了一種基于跳躍連接深度神經網絡的非接觸故障診斷方法進行閥門泄漏故障診斷，準確率達到98.89%。Cheliyan 和Bhattacharyya[16-17]采用模糊故障樹和非支配排序遺傳算法進行了采油樹可靠性分析。劉超等[18-19]基于歷史數據和失效模式分析，應用馬爾可夫模型（Markov）、FFTA 及FMEA 對采油樹進行可靠性評估，得到采油樹可用度為0.999 671；并通過概率重要度分析明確了油管懸掛器化學試劑注入耦合器、節流模塊硬管及控制閥是薄弱環節，概率重要度達到了0.999 797。劉健等[20]利用動態模糊子集來描述貝葉斯網絡各根節點動態失效概率，很好地解決了因部件故障信息的模糊性與動態性造成的求解精度偏低的問題。

以上針對采油樹關鍵部件進行失效分析的研究達到了較好的可靠性指標評估效果，但目前針對采油樹關鍵部件的可靠性研究多集中在閥門、油管懸掛器、井口連接器、控制模塊以及框架結構方面，對采油樹生產回路可靠性的分析較少。本文對采油樹生產回路進行可靠性和可用性分析，解決生產回路的實時運維評估問題；同時，在現有可靠性研究基礎上增加反饋功能，即考慮生產回路維修性數據補充到可靠性評估模型中，達到完善可靠性評估模型變量節點的目的。

1 深水采油樹生產回路

本節針對深水采油樹生產回路的結構組成、執行功能以及工作原理等方面進行分析，為建立3 條回路的隨機Petri網運維模型提供建模基礎。

采油樹生產回路主要承擔深水采油樹的油氣傳輸和流量控制的工作。如圖1 所示，當系統正常工作時，打開水下控制安全閥，海底油氣通過生產回路采集，依次通過生產主閥，生產翼閥和生產節流閥。在閥門周圍布置傳感器，負責接收溫度、壓力以及沙粒沖蝕等信號，并傳送到水下控制系統進行實時監測。當PTT1數據反饋大于額定值時，水下控制系統發送信號使生產主閥中電液換向閥斷電，彈簧復位關閉生產主閥，如果PTT1仍然顯示數據，說明生產主閥故障，需要進行修復并保證正常運行，如不能及時維修，則需要關閉生產翼閥，若此時隔離仍不成功，說明生產翼閥故障，則需要繼續關閉節流閥和隔離閥。生產節流閥通過閥門打開程度控制生產回路中油氣流量，流量計WGFM 統計生產回路實時流量并反饋給水下控制系統。當生產回路的傳感器數據反饋小于額定值時，水下控制系統只能接收數據，無法關閉閥門，需要水下機器人操作深水采油樹控制面板強行關閉閥門。當生產回路中的閥門無法正常關閉時，深水采油樹將進入危險狀態。

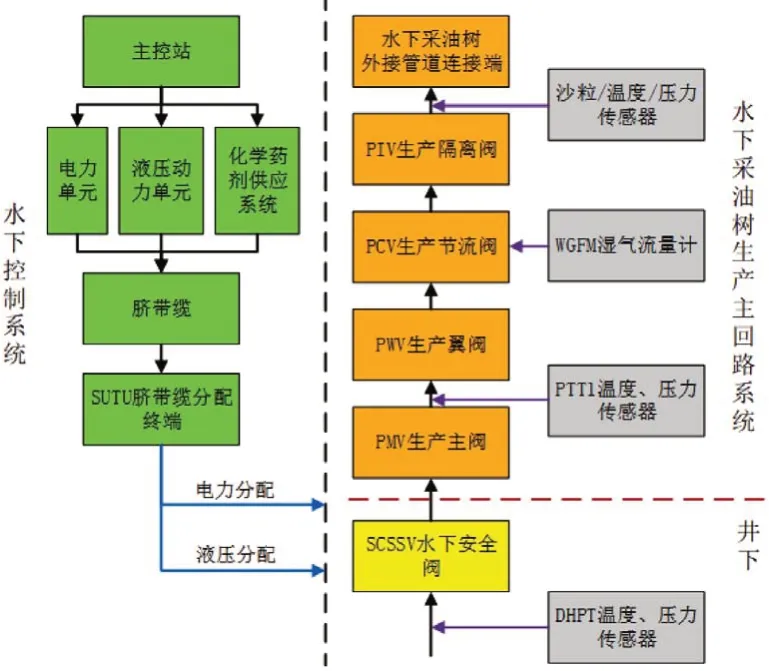
圖1 深水采油樹生產回路

2 隨機Petri網模型

深水采油樹生產回路較為復雜，存在兩種或多種失效模式同時發生的情況，為避免可靠性分析過程中的爆炸性問題，本文采用隨機Petri 網法進行可靠性分析，首先介紹隨機Petri網應用原理和建模流程。

2.1 隨機Petri網

隨機Petri 網（SPN）系統定義為六元組N=（P，T，F，K，M0，λ），其中（P，T，F）為基網；K為容量函數；M0為初始標識；λ為變遷T轉移率的集合，即故障率。故障率與標識狀態無關，一般假設元器件隨機Petri網中故障率服從指數分布，結構件隨機Petri 網中故障率服從威布爾分布。基網定義為三元組N=（P，T，F），P為庫所，T為變遷，F為連接弧，滿足以下4 點；（1）P∩T= ?，庫所和變遷應沒有交集；（2）P∪T≠?，網中至少要有一個元素；（3）F?P×T∪T×P，弧分為兩類；（4）dom(F)∪cod(F)=P∪T，網中無孤立元素。其中，dom(F)={x|?y.(x,y)∈F} ，為定 義 域； cod(F)={x|?y.(y,x)∈F} ， 為 值 域；P={P1,P2,…,Pn} ， 為 一 個 有 限 的 庫 所 集 合；T={t1,t2,…,tq} ，為一個有限的變遷集合；n為庫所總數，pi為一個庫所，即系統一個局部的狀態；P為整個系統的狀態；q為變遷總數。在一個Petri 網系統中，可以通過Token 來表示庫所的狀態，用m（pi）表示庫所Pi的Token值，則Token 的分布狀態為系統的整體狀態，稱之為標識，則定義M0=[m（0P1），m（0P2），…，m（0Pn）]為初始標識，代表系統的原始狀態。

2.2 生產主閥PMV的隨機Petri網模型

針對生產主閥PMV 的運行狀態由正常運行到發生泄漏，發生泄漏后確定PMV 失效，然后發現失效，發起命令進行維修，最后通過維修恢復PMV 正常工作狀態。該變遷過程如圖2 所示，系統初始標識M0=[1，0，0]，此時變遷failure 具有發生權。由于PMV 屬于液壓元器件，失效和維修分布一般符合指數函數，發現失效后發起開始維修命令符合零延遲狄拉克定律。

2.3 隨機Petri網建模流程

在隨機Petri 網絡中，對系統在不同狀態可能發生的事件（故障、測試、維護等）進行建模。過程如下：

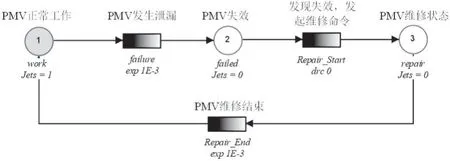
圖2 PMV網系統模型

（1）首先列出系統所有庫所和變遷：明確深水采油樹生產回路不同狀態以及不同狀態之間的轉換過程；

（2）確定庫所和變遷邏輯關系：明確每個變遷的輸入和輸出；

（3）確定所有變遷發生分布函數：一般閥門、傳感器、流量計等電控、液壓元器件的失效模式一般服從指數分布；機械結構的失效模式一般服從威布爾分布；

（4）建立系統隨機Petri 網模型：根據庫所、變遷以及庫所和變遷的邏輯關系建立深水采油樹生產回路的隨機Petri網模型；

（5）完成可靠性及可用性等分析：基于系統隨機Petri 網模型和變遷發生分布函數關系，完成深水采油樹生產回路的可靠性和可用性指標求解。

3 深水采油樹生產回路可靠性分析

建立Petri 網模型之前，根據系統實際工作情況和可靠性基礎知識作如下假設：

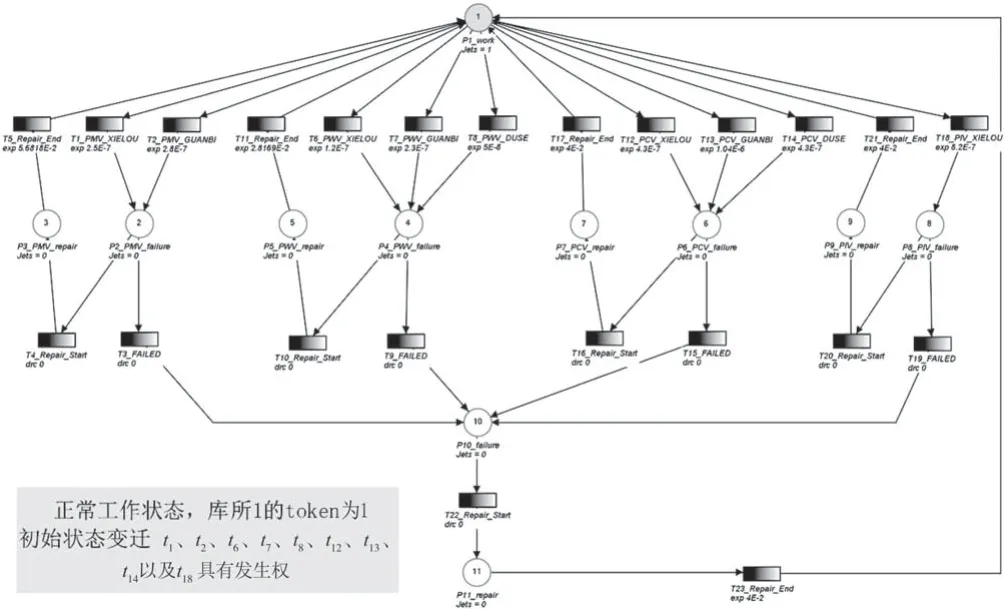
圖3 生產回路Petri網模型

（1）系統中所有部件和元器件的技術參數都滿足設計要求，且從完美狀態開始工作；

（2）閥門、傳感器、流量計等電控、液壓元器件失效率的失效模式均服從指數分布；機械結構部件失效率的失效模式均服從威布爾分布；

（3）各失效模式均互不影響，相互獨立；

（4）忽略控制系統的失效。

基于第2節深水采油樹生產回路分析，建立如圖3所示的深水采油樹生產回路的隨機Petri網模型。

該模型中包括11個庫所：

（1）庫所1：work，生產回路運行正常狀態；

（2）庫所2：failure，PMV故障狀態；

（3）庫所3：repair，PMV維修狀態；

（4）庫所4：failure，PWV故障狀態；

（5）庫所5：repair，PWV維修狀態；

（6）庫所6：failure，PCV故障狀態；

（7）庫所7：repair，PCV維修狀態；

（8）庫所8：failure，PIV故障狀態；

（9）庫所9：repair，PIV維修狀態；

（10）庫所10：failure，生產回路故障狀態；

（11）庫所11：repair，生產回路維修狀態。

模型的23 個變遷如表1 所示（失效和維修率數據來源于OREDA海洋工程可靠性手冊）。

該模型可以用來模擬深水采油樹生產回路實際運行流程：

（1）庫所1 最初包含一個token，因此進行失效轉換是初始狀態唯一有效的轉換；

（2）當生產回路發生任一失效時，按照失效模式發生的分布函數進行變遷。此時，生產回路運行正常狀態的token將被設置為0，失效模式所在庫所token數為1；

（3）當失效模式發生時，會分為是否進行維修兩種狀態，且兩種狀態觸發變遷不同，如當PMV 發生泄漏，分為發現泄漏失效和沒有發現失效兩種情況，如果發現泄漏失效，則Repair_Start 變遷傳遞為true，PMV 進入維修狀態；如果沒有發現泄漏失效，則沒有發現PMV 失效的變遷傳遞為true，PMV 長期處于泄漏狀態，會導致生產回路失效；

表1 隨機Petri網模型的23個變遷信息

（4）一旦修復開始（Repair_Start 變遷傳遞為true），水下控制系統會立刻發出指令，關閉相應元器件并進行維修，因此修復將立即開始，設置修復變遷的延遲定律為零延遲狄拉克定律，token直接轉移到維修狀態的庫所；

（5）token 到達正常工作狀態的庫所按照Repair_End變遷的分布函數進行；

（6）啟動Repair_End 變遷后將從Repair 狀態刪除token，將一個token 放入Work 位置。因此生產回路回到正常工作狀態。

4 生產回路可靠性仿真、結果分析及驗證

4.1 可靠性仿真

在仿真模式下，當Petri 網模型中變遷有效時，變遷可以隨設定的分布函數進行觸發，也可以自動觸發，自動觸發零延遲（參數為0 的狄拉克定律）的變遷。在幾個狄拉克變遷“沖突”的情況下，這些變遷的發生是根據它們的優先級進行的，按照時間順序進行。本節對生產回路進行可靠性仿真分析。

根據生產回路隨機Petri 網模型可知，N=（P，T，F，K，M0，λ），其中P={p1，p2，p3，p4，p5，p6，p7，p8，p9，p10，p11}；T={t1，t2，t3，t4，t5，t6，t7，t8，t9，t10，t11，t12，t13，t14，t15，t16，t17，t18，t19，t20，t21，t22，t23}；F={（p1，t1），（p1，t2），（t1，p2），（t2，p2），（p2，t3），（p2，t4），（t3，p10），（t4，p3），（p3，t5），（t5，p1），（p1，t6），（p1，t7），（p1，t8），（t6，p4），（t7，p4），（t8，p4），（p4，t9），（p4，t10），（t9，p10），（t10，p5），（p5，t11），（t11，p1），（p1，t12），（p1，t13），（p1，t14），（t12，p6），（t13，p6），（t14，p6），（p6，t15），（p6，t16），（t15，p10），（t16，p7），（p7，t17），（t17，p1），（p1，t18），（t18，p8），（p8，t19），（p8，t20），（t19，p10），（t20，p9），（p9，t21），（t21，p1），（p10，t22），（t22，p11），（p11，t23），（t23，p1）}；M0={m0（p1）=1，m0（p2）=m0（p3）=m0（p4）=m0（p5）=m0（p6）=m0（p7）=m0（p8）=m0（p9）=m0（p10）=m0（p11）=0}，因此初始狀態變遷t1、t2、t6、t7、t8、t12、t13、t14以及t18具有發生權。

4.2 可靠性結果分析及驗證

圖4 所示為深水采油樹生產回路失效率對平均無故障時間的影響。系統MTTF 隨失效率的增加而減小，根據OREDA 數據庫推薦的失效率進行計算，生產回路平均無故障時間為9 998.2 h。系統的可用度可以表示為系統平均無故障時間與平均無故障時間和平均維修時間加和的比值，根據生產回路隨機Petri 網模型可求得系統的平均維修時間，如表2所示。

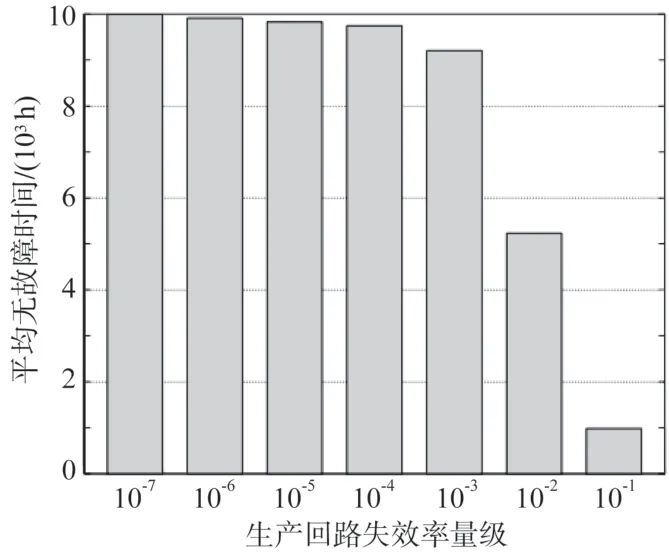
圖4 生產回路失效率對平均無故障時間的影響

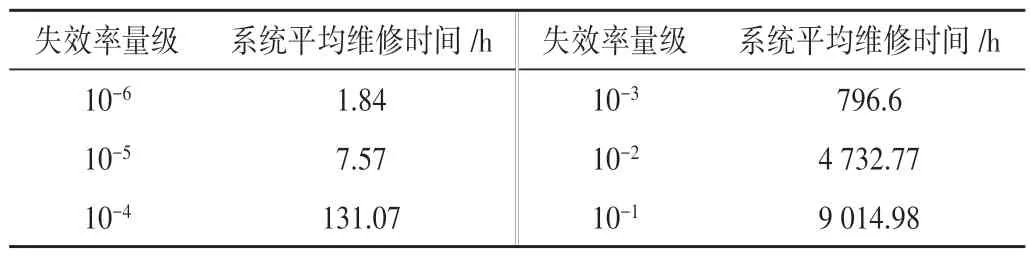
表2 生產回路不同失效率的平均維修時間

由OREDA數據庫可知，當失效率量級達到10-6～10-4時，系統平均維修時間在0.3～456.0 h內，本文得出1.84、7.57、131.07 h 均符合系統平均維修時間取值范圍。圖5所示為深水采油樹生產回路失效率對生產回路可用度的影響。由圖可知，系統可用度隨失效率增加而減小，當失效率低于10-3時，生產回路的可用度下降趨勢比較平緩，當失效率大于10-3時，可用度隨故障率的增加而迅速下降。根據OREDA 數據庫推薦的失效率計算，生產回路可用度為0.999 8。

圖5 深水采油樹生產回路失效率對系統可用度的影響

5 結束語

本文針對深水采油樹生產回路進行可靠性分析，提出了基于隨機Petri 網的運維可靠性分析方法，避免了可靠性分析過程中的爆炸性問題，得到主要結論如下：

（1）考慮系統維修性的影響，對深水采油樹生產回路進行可靠性分析，得到了平均無故障時間及可用性曲線；

（2）通過隨機Petri 網可靠性模型分析，得到了采油樹生產回路不同失效率情況下系統的平均維修時間，如針對生產回路，當失效率分別為10-6、10-5、10-4、10-3、10-2和10-1時，系統平均 維修時間 分 別為1.84、7.57、131.07、796.6、4 732.77、9 014.98 h，以上結果通過了OREDA數據庫的數據驗證；

（3）通過隨機Petri 網可靠性模型分析，得到了不同失效率情況下，采油樹生產回路的可靠度；同時基于OREDA 數據庫統計的失效率進行計算，得到深水采油樹生產回路的平均無故障時間約為9 998.2 h。