基于改進灰狼算法的火電廠濕法脫硫模型辨識
馮江濤,榮矗嗣,李翰章,王晨光
(1.山西大學 自動化與軟件學院,太原 030000;2.山西昱光發電有限責任公司,朔州 036000)
火力發電作為電力行業壓艙石,在我國能源領域占據重要地位。SO2為火電廠排放主要污染物之一,每年由火電廠燃煤所排放的SO2總量達到全國SO2排放總量的一半以上[1],因此探索火電廠SO2超低排放控制具有重要意義。
石灰石-石膏濕法煙氣脫硫技術在已投產的火電機組中市場占有率最高[2]。通過調研,濕法脫硫技術在多臺火電機組中采用人工方法,人力資源成本很高。究其原因,火電機組因其運行工況復雜,使得無法獲取濕法脫硫系統的數學模型,由此制定的控制方案魯棒性差。
許多學者致力于濕法脫硫系統建模,文獻[3]提出使用數據挖掘的方法完成火電機組優化運行;文獻[4]根據廠級SIS 系統數據,使用改進粒子群算法完成脫硫模型辨識,粒子群算法所需調節參數較少,易于實現,但其容易陷入局部最優;文獻[1]提出根據廠級SIS 系統數據,使用改進差分算法實現脫硫模型辨識,差分進化算法具有收斂快,控制參數少等優點,但其仍面臨早熟收斂與搜索停滯問題[5]。以上方法基于建模理論給出單一工況下建模結果,對火電機組濕法脫硫建模有啟發性作用,本文針對某火電機組濕法脫硫系統的設備配置,基于廠級SIS 系統數據,采用IGWO 完成兩種工況濕法脫硫系統的模型辨識,為濕法脫硫的自動控制研究提供技術基礎。
1 火電機組濕法脫硫系統模型結構
1.1 某火電機組的濕法脫硫工藝系統
火電機組濕法脫硫系統主要包括石灰石漿液系統、吸收系統、煙氣系統、石膏脫水系統、廢水處理系統、事故漿液排放系統和電氣與監測控制系統等7 個子系統[6]。原煙氣由引風機送入煙道之中,在煙道中與噴淋層中的石灰石漿液反應,進而去除煙氣中的SO2,其中噴淋層范圍如圖1 所示,其受漿液循環泵啟停數量影響;而噴淋層中的脫硫效率則受到漿液pH 值影響(pH 值為5.6 左右脫硫效率最高)[4],其通過石灰石漿液控制閥開度控制。

圖1 循環泵數量與煙氣反應區間關系Fig.1 Relationship between the number of circulation pumps and the flue gas reaction interval
1.2 脫硫系統模型結構
1.2.1 模型輸出
由1.1 節內容可知,石灰石漿液pH 值影響脫硫效率,凈煙氣SO2濃度為火電廠濕法脫硫系統主要監測變量,綜合考量以上因素,本文選取凈煙氣SO2含量與漿液pH 作為本次所識別模型的輸出。考慮到漿液循環泵運行數量會影響脫硫工況,因此本文將分別對4 臺漿液循環泵工況(以下簡稱工況1)與5 臺漿液循環泵工況(以下簡稱工況2)下脫硫模型進行辨識。
1.2.2 模型輸入
火電機組的監測參數多,且存在參數之間相互耦合、影響問題,若將所有數據都作為模型輸入則計算量龐大,因此,本文通過構建決策樹,采用分類回歸樹(classification and regression tree,CART)算法,完成特征重要性排列,從而實現模型輸入參數的選擇。
以石灰石漿液pH 值與凈煙氣SO2濃度為輸出,選擇石灰石漿液流量、原煙氣流量等作為輸入變量分別構建決策樹,所得各特征重要性如表1所示。

表1 重要性分析結果Tab.1 Significance analysis results
由表1 可知,石灰石漿液流量、原煙氣流量對漿液pH 值和凈煙氣SO2濃度的影響最大;原煙氣SO2濃度影響次之,鍋爐負荷、給漿密度、母管壓力及原煤耗對輸出影響均小于0.10,因此認定其對輸出結果影響較小,將其從輸入變量組舍棄,將石灰石漿液流量、原煙氣流量、原煙氣SO2濃度置于輸入變量組之中。
1.3 系統模型結構
1.3.1 傳遞函數選擇
工程研究過程中,常用傳遞函數的形式表達實際工況中的某一環節,為方便研究,通常采用主導極點代替全部閉環極點來估算系統性能指標[7]。其原理為傳遞函數對于輸出的影響主要通過主導極點表示。此外,濕法脫硫系統為大遲延系統,需在傳遞函數中加入遲延環節,基于以上原理,本文初步選擇二階多容慣性加純遲延形式的傳遞函數,作為本文的傳遞函數模型,如式(1)所示:
式中:G(s)為傳遞函數;K 為放大系數;T 為時間常數;τ 為遲延時間。
1.3.2 系統模型結構
首先使用三輸入雙輸出作為本文所需辨識的系統模型,其結構如圖2 所示。qCaCO3(s)、qSO2,in(s)、mSO2,in(s)為系統輸入,分別表示石灰石漿液流量,原煙氣流量及原煙氣SO2濃度;yPH(s)表示石灰石漿液pH 值;ySO2(s)表示凈煙氣SO2濃度。以圖2 中G12(s)為例,所需辨識參數為k12、τ12、T12以及T12′。
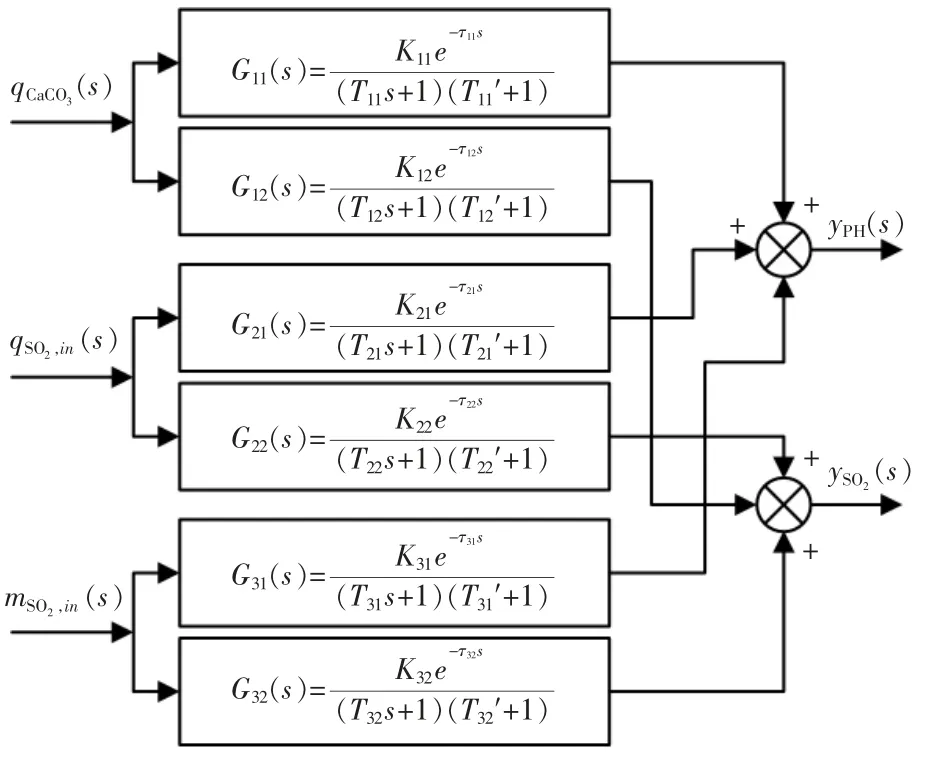
圖2 系統模型結構Fig.2 System model structure
2 改進灰狼算法
2.1 灰狼算法
通過模擬狼群捕食規律,文獻[8]提出使用灰狼算法(grey wolf optimizer,GWO)完成參數尋優工作。灰狼算法將種群分為4 個階層,Alpha 狼、Beta 狼、Delta 狼與其他灰狼,其位置更新公式如式(2)與式(3)所示:
2.2 算法改進
為避免灰狼算法在迭代過程中過早收斂,陷入早熟,本文提出改進灰狼算法(improved grey wolf optimizer,IGWO),其中,式(5)中參數在尋優過程中由[2,0]范圍內線性衰減,當值位于[2,1]范圍中時,算法傾向于全局搜索,當值位于[1,0]范圍中時,算法傾向于局部搜索,本文將其衰減過程設置為拋物線下降,以增強其全局搜索能力;嵌入萊維飛行[9],進一步強化其全局搜索能力;同時在位置更新時加入貪婪算法,進一步提高算法的尋優能力。改進后的灰狼位置更新規則如式(9)所示:
式中:α⊕Levi(β)滿足式(10)關系,其中u 與v 均服從正態分布:
本算法流程如圖3 所示。
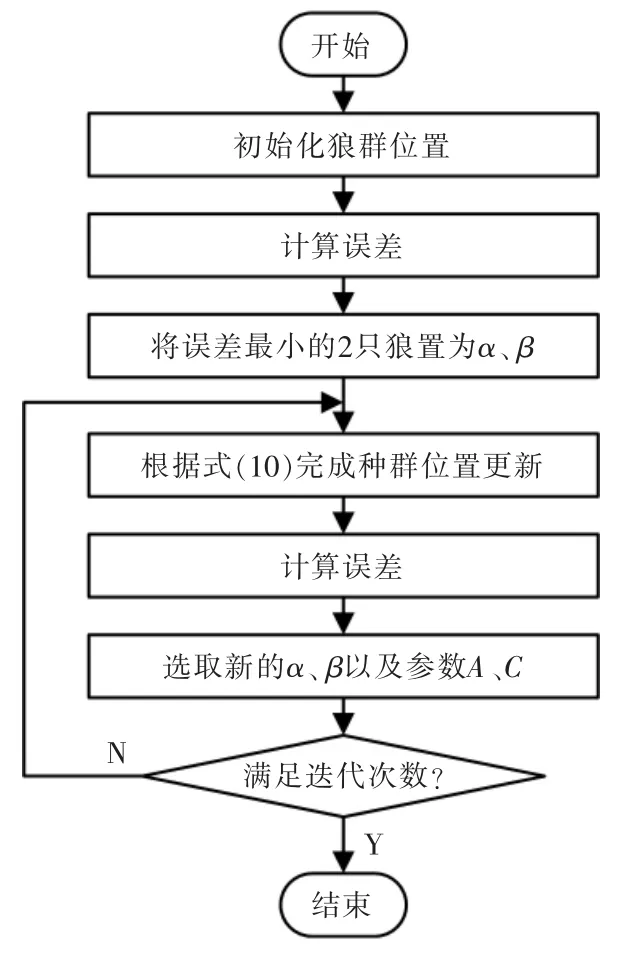
圖3 IGWO 算法流程Fig.3 Flow chart of IGWO algorithm
2.3 優化效果
為驗證本文使用的灰狼算法的性能,本文使用GWO算法與IGWO 算法分別對標準測試函數進行優化,通過比較在相同迭代次數下的誤差值,驗證本文所提出方法的優越性,其中所使用標準測試函數為
測試結果如圖4 所示,由測試結果可知IGWO在相同迭代次數下收斂效果優于傳統GWO 算法,IGWO 的尋優能力更為出色。

圖4 測試函數結果Fig.4 Test function results
3 濕法脫硫系統模型辨識
脫硫塔漿液pH 與凈煙氣SO2含量為本文模型輸出,為得到貼合實際的火電廠濕法脫硫系統模型,首先選取圖2 所示三輸入雙輸出結構作為初步辨識模型,選取某火電廠2×350 MW 機組工況1 與工況2 下,兩組歷史數據完成建模與驗證工作,兩組數據包括石灰石漿液流量、原煙氣流量、原煙氣SO2濃度、凈煙氣SO2濃度以及石灰石漿液pH 值。以工況1 下數據為例,其前24000 s 數據用于建模,后21000 s 數據用于驗證所建模型的準確性。
3.1 數據處理
3.1.1 零初始化處理
對于所采取到的實際數據而言,其平衡點并非位于系統實際的零值點,且輸入輸出數據的零點是隨意的,因此為得到與信號零點無關的傳遞函數,需對數據進行零初始化處理,處理方法如式(12)所示:
式中:N 為零初始點個數,一般取4~6 點數據[10]。
3.1.2 粗大值處理
粗大值處理中有較多的粗大值判別準則,其中3δ 準則多被用于數據較多且對精度要求不高的數據[11],此準則適用于本文數據,因此選擇此準則作為本文數據處理的標準。
(1)標準差計算
式中:n 為數據個數;xn為第n 個數據的數據值;為此組數據的平均值。
(2)逐一對此組數據進行判斷
若該點數據滿足式(14),則保留該點數據;若不滿足,則使用式(15)對該點數據進行處理:
3.1.3 數據平滑處理
經過粗大值處理后的數據仍會出現部分“毛刺”,為使模型辨識結果更為準確,本文通過平滑處理方法[12],使得數據更易于辨識。本次平滑處理采用高斯濾波器,其長度為100。
以工況1 下石灰石漿液pH 辨識數據為例,其數據處理前后對比如圖5 所示。
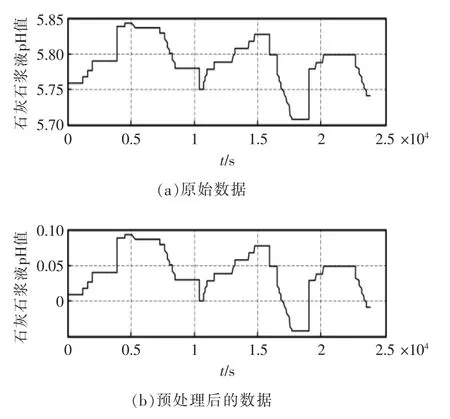
圖5 數據處理結果Fig.5 Data processing results
由圖5 所示可知,經數據處理后,數據連續性變好,采樣點間過度更為平滑。本文其余數據均采用此數據處理方法。
3.2 模型參數辨識
3.2.1 工況1 下模型參數辨識
辨識所得仿真曲線如圖6 和圖7 所示。如表2所示,對建模誤差進行定量分析,分別計算所建模型在辨識數據集與測試數據集誤差,誤差計算方法為均方誤差(mean square error,MSE)。通過對圖6、圖7 與表2 數據綜合分析,辨識所得模型輸出走勢與實際值相同,且誤差較小,滿足實際生產需求。

表2 輸出變量為石灰石漿液pH 值的仿真誤差Tab.2 Simulation error with output variable as limestone slurry pH
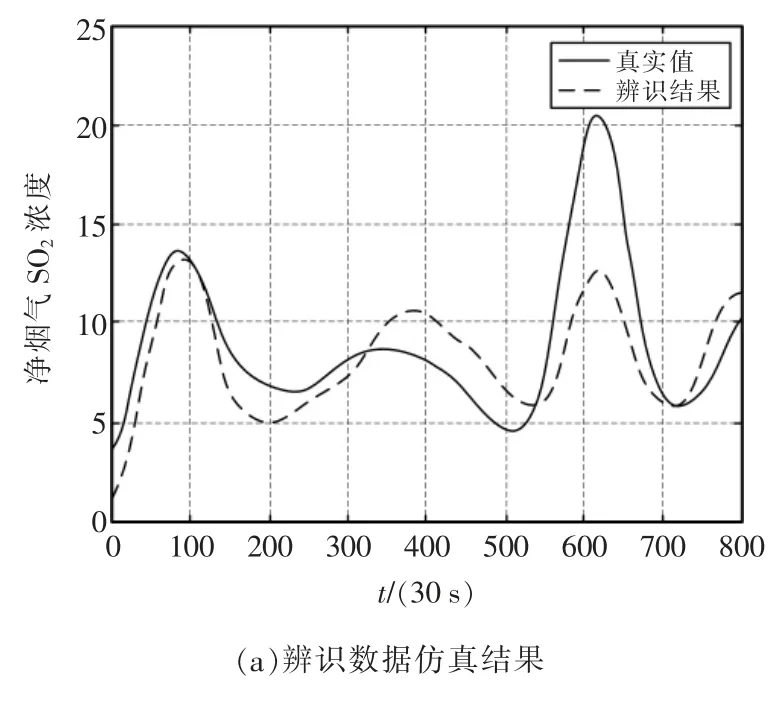
圖6 輸出變量為凈煙氣SO2 濃度的辨識結果Fig.6 Identification results for output variable of net flue gas SO2 concentration
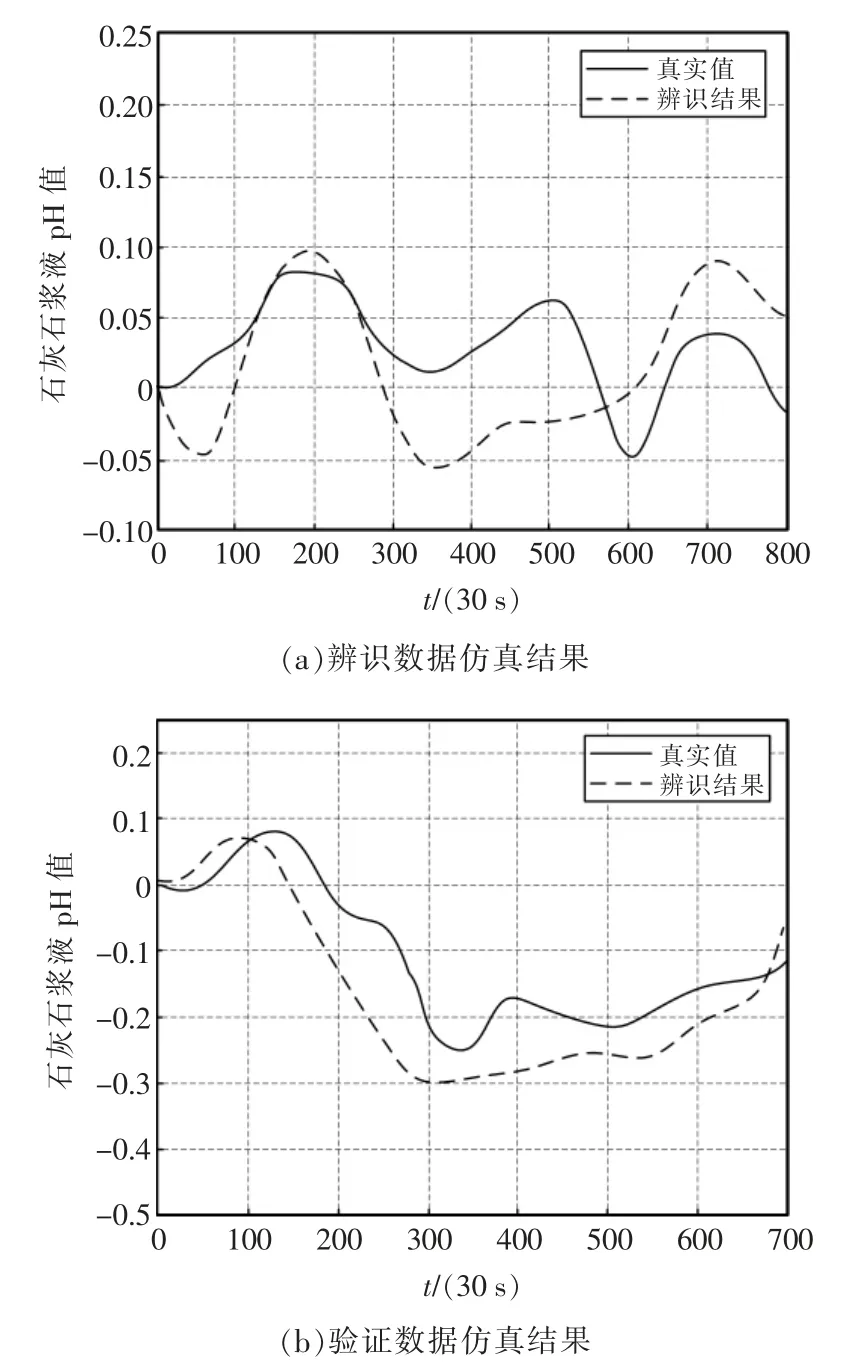
圖7 輸出變量為石灰石漿液pH 值的辨識結果Fig.7 Identification results of output variable as limestone slurry pH
在工況1 下,以石灰石漿液pH 值為輸出變量,所得模型為
以凈煙氣SO2濃度為輸出變量時,其模型為
3.2.2 工況2模型辨識
收集工況2 下廠級SIS 系統中的歷史數據,完成該負荷下模型辨識,辨識結果如圖8 和圖9 所示。

圖8 輸出變量為凈煙氣SO2 濃度辨識結果Fig.8 Output variable is the net flue gas SO2 concentration identification result
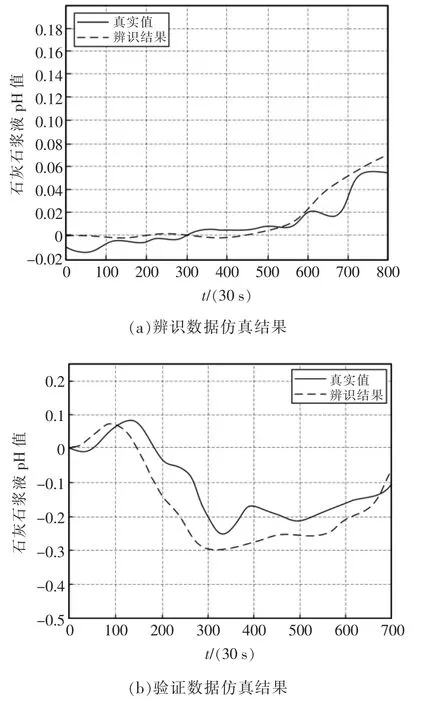
圖9 輸出變量為石灰石漿液pH 值辨識結果Fig.9 Output variable is limestone slurry pH identification result
工況2 下所得模型的辨識誤差與驗證誤差,如表3 所示,其結果符合預期目標。

表3 工況2 負荷辨識與驗證誤差Tab.3 Identification and validation errors of working condition 2 load
其中工況2 下,以凈煙氣SO2濃度為輸出變量時的辨識結果為
以石灰石漿液pH 值為輸出變量時的辨識結果為
3.3 結果分析
使用三輸入雙輸出結構完成不同工況下火電廠濕法脫硫模型辨識工作,在工況1 與工況2 下,本文辨識所得模型與實際值變化趨勢相近且均方誤差較小,符合工程研究需求。
4 結語
利用火電廠SIS 系統中的歷史數據,通過特征重要性理論對火電廠眾多數據進行分析,引入改進灰狼算法完成火電機組濕法脫硫模型辨識,實現不同工況下火電廠濕法脫硫系統的建模,為濕法脫硫的自動化控制提供了基礎。
本文僅基于兩種工況下的SIS 系統數據進行建模,深度調峰情況下(漿液循環泵啟用數≤3)的SIS系統連續數據較少,無法完成辨識工作,因此深度調峰工況下的火電廠濕法脫硫模型辨識工作將是之后工作推進的方向。

