以大概念驅動單元整體教學

李玲靜

［摘 要］圖形與幾何領域的大概念是對圖形的形狀和特性進行描述、分類和分析。以“認識三角形”教學為例，從單元整體視角出發，讓學生經歷圖形分類、數學實驗等活動，幫助學生發展空間觀念。

［關鍵詞］大概念；單元整體教學；三角形

［中圖分類號］ G623.5 ［文獻標識碼］ A ［文章編號］ 1007-9068（2023）23-0048-03

大概念包括學科大概念、領域大概念以及單元核心概念和課時具體認知概念，教師要梳理它們之間的上下位關系，只有理解了這幾個大概念的上下位關系，才能設計好知識與技能的學習路徑。而單元的重組與統整能真正體現知識的結構化和聯系性。本文聚焦圖形與幾何領域中的“圖形的認識與測量”主題，以北師大版教材四年級下冊的“認識三角形”為例，探討以大概念驅動單元整體教學的方法。

一、單元內容分析

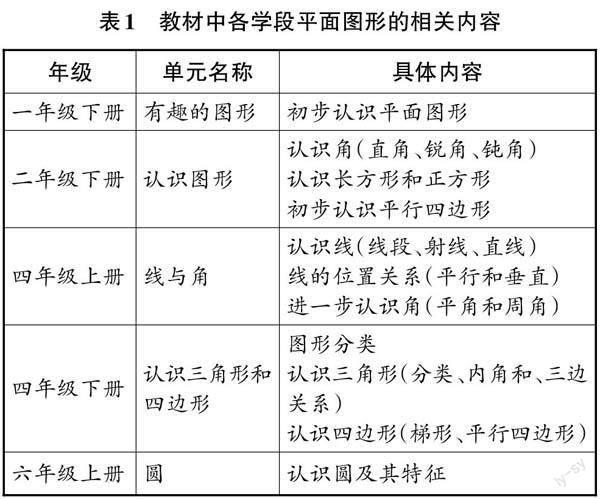
《義務教育數學課程標準（2022年版）》中將圖形與幾何領域的內容統整為“圖形的認識與測量”和“圖形的位置與運動”兩個主題。“圖形的認識與測量”包括立體圖形和平面圖形的認識、線段長度的測量以及圖形周長、面積和體積的計算。“認識三角形”屬于認識平面圖形范疇，平面圖形的相關內容在教材中的編排見表1。

可見，在學習有關三角形的知識之前，學生對平面圖形有了一些認識，特別是在認識長方形、正方形、平行四邊形的活動中已經知道，可以從“邊”和“角”兩個維度展開研究。筆者將教材中三角形的主要內容進行了梳理，并整理成圖（如圖1）。

從圖1可知，教材中三角形的內容主要有三角形的穩定性、分類、內角和、三邊關系。值得一提的是，北師大版教材將三角形的定義融入其他知識點中。因此，在教學三角形的知識時，教師應主要講授其概念和性質。

二、大概念驅動課時設計

三角形內容教學的大概念是研究三角形的形狀和特性，所指向的核心概念是發展學生的空間觀念、推理意識和抽象意識。具體認知概念是根據圖形的形狀和特性進行具體化描述、分類和分析，比如，可以從邊和角度來描述三角形；可以由其他多邊形構造或分解出三角形；可以根據邊的關系和角的大小來分類和命名三角形等。這一系列的具體化認知概念為大單元教學提供了課時設計思路。“認識三角形”的課時內容安排及課時目標見表2。

三、單元整體教學課堂實踐

基于以上對大概念的認識和對單元知識結構的分析，筆者進行了課堂實踐，具體課例如下。

【課例1：三角形單元準備課】

活動一：剪出幾個不一樣的三角形，觀察三角形的特征。

活動二：分別用3根和4根小棒擺出三角形和四邊形，并嘗試拉動，把第一次擺好的圖形和拉動后的圖形形狀畫下來，研究三角形的穩定性。

活動三：思考如何讓不穩定的四邊形變成穩定的三角形。

【設計意圖】

為了讓學生全面體驗三角形的類型及特性，本節主要采取活動課的方式，通過讓學生動手剪三角形體會三角形的多樣性，同時也讓學生明白對三角形進行分類的必要性。學生通過動手擺小棒、拉一拉三角形和四邊形，并畫出原圖和拉動后的圖形，化動為靜，以此歸納三角形的穩定性質，發展學生的空間觀念和抽象意識，讓學生運用所學知識解釋生活現象，感受數學與生活的關系。

【課例2：三角形的分類】

活動一：將不同的三角形分類。

第一種情況：按角分。

基本特征：銳角三角形有3個銳角，鈍角三角形有1個鈍角和2個銳角，直角三角形有1個直角和2個銳角。

第二種情況：按邊分。

基本特征：等邊三角形的三條邊相等，等腰三角形有兩條邊相等，不等邊三角形沒有相等的邊。

【設計意圖】

分類是一種把具有相同特征的事物歸到一起的科學方法，是人們認識事物的一種思想方法。對三角形進行分類，其核心是對三角形邊和角本質屬性的特征進行描述和分析。

【課例3：三角形的內角和】

活動一：量一量，猜想三角形的內角和是180°。

活動二：驗證猜想。

1.活動建議

給每一位同學一個信封，信封內有三角形和四張“智慧卡”，分別是A、B、C卡和挑戰卡。這四張卡上有關于探索三角形內角和的不同提示，通過層層提示引導學生完成三角形內角和的探究活動。

（1）先看智慧A卡，如果有困難，可以看B卡，依此類推。

（2）如果還有困難，可以和老師一起研究。

2.反饋交流

方法一：剪、撕、拼。

方法二：折、拼、畫。

方法三：推理。

幾何畫板演示：所有直角三角形都可以從長方形中分割而來，內角和都是180°。

活動三：你能利用“已知直角三角形的內角和是180°”這個結論來驗證銳角三角形和鈍角三角形的內角和嗎？動手試試看吧！

教師展示學生驗證過程（如圖2）。

【設計意圖】

用“猜想—驗證”的思想來設計活動過程，首先引導學生通過量一量猜想“三角形的內角和是180°”，再通過驗證完成認知。大部分學生對實驗操作得到的結論都確信，但也有個別學生有批判精神，提出由撕拼、折拼而成的角看似平角，但不一定是平角，將所有學生的思維引向深處。教師適時帶領學生探索如何把銳角三角形和鈍角三角形轉化為直角三角形來解決，讓學生經歷了推理過程，形成了一定的推理意識，發展了學生的空間觀念。

【課例4：三角形的三邊關系】

活動一：將一根吸管任意剪成三段，都能圍成三角形嗎？

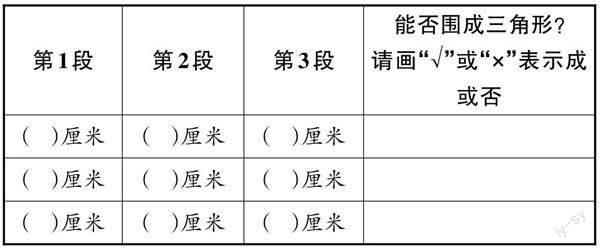
1.合作完成以下學習單

2.反饋

問題1：有些為何圍不成三角形？（兩邊之和小于第三邊）

問題2：有些為何能圍成三角形？（兩邊之和大于第三邊）

活動二：辨析識本質——這幾段能圍成三角形嗎？合作完成以下學習單。

【設計意圖】

對三角形三邊關系的理解離不開直觀的感悟，因此本節課中，教師用一根吸管作為學具，圍繞能否圍成三角形的活動目標展開教學。首先猜想是不是任意將吸管剪成三段都能圍成三角形，然后從圍成的三角形的過程中得知原因——三角形任意兩邊之和大于第三邊。活動二是拓展延伸，培養學生的抽象意識和推理意識。

四、大概念驅動教學的啟示

《義務教育數學課程標準（2022年版）》中指出，教師要重視單元整體教學設計，改變過于注重以課時為單位的教學設計，推進單元整體教學設計，體現數學知識之間的內在邏輯關系，以及學習內容與核心素養表現的關聯。大概念驅動下的整體教學設計在整體分析單元內容本質和學生認知概念的學情基礎上，確定單元的教學內容及目標，分步落實在各個環節中，主要有以下幾個優勢。

1.關注結構化分析，尋找大概念

尋找三角形單元的大概念要經歷幾個階段。第一階段是縱向分析三角形知識所處的位置，再橫向分析三角形單元內容結構，主要圍繞三角形穩定性、分類、邊、角研究。第二階段是尋找具體認知概念，從知識本質的角度進行分析。第三階段是學科核心概念定位，錨定空間觀念、幾何直觀、抽象意識、推理意識四個核心概念。第四階段是三角形單元整體教學的大概念統攝，由于三角形的內容屬于圖形與幾何領域，因此利用圖形的大概念對三角形的形狀和特性進行分類、描述和分析。

2.要以單元為單位，設核心問題

要樹立整體意識，把單元中出現的關聯內容緊密聯結在一起，形成拓撲結構圖，再通過核心問題串聯，比如，“如何研究這些不一樣的三角形”“將不同的三角形進行分類”“三角形內角和是180°”“將一根吸管任意剪成長度不同的三段，這三段一定能圍成三角形嗎？”等，讓學生對三角形有深入的認識和理解，發展學生的空間觀念、幾何直觀、推理意識、抽象意識，提升學生的數學核心素養。

3.關注活動的一致性，達深度學習

課例1的主要活動是剪三角形，初步感悟三角形的種類和特性，課例2的主要活動是將三角形進行分類，課例3的活動是對三角形撕、拼、推理，課例4的活動有剪、圍等操作。對概念和性質的理解都離不開直觀的活動，這一系列的課中設計了許多動手操作活動，旨在幫助學生形成表象，建立良好的空間觀念，為推理、抽象意識的發展打下堅實的基礎，也體現了活動的一致性，在簡單活動中逐步深入，達成深度學習的目標。

總之，以大概念驅動的單元整體教學目標指向核心素養，教師在教學中要多思考，尋找與內容對應的大概念，以核心問題推進單元整體教學，優化課堂結構，幫助學生提升數學核心素養。

（責編 黃 露）