串聯(lián)機器人模態(tài)仿真與實驗

陳昊然，張 宇，段昊宇翔，謝 康

(昆明理工大學 機電工程學院，云南 650500)

0 引言

工業(yè)機器人是一種由多種技術集成來滿足實際加工和生產需求的工業(yè)裝備[1-3]。因工業(yè)機器人具有較好的可編程性以及良好的適應性，使其已成為現(xiàn)代智能制造業(yè)不可或缺的重要裝備[4]。近年來，串聯(lián)機器人在工業(yè)生產中的地位逐漸提升，其在工業(yè)生產線的工作場景和內容較為復雜，這就對機器人的動態(tài)性能、剛度性能等方面提出了更高的要求[5-6]。因此，提高機器人的動態(tài)性能，對其滿足高性能要求具有重要意義。

串聯(lián)機器人一般利用交流伺服驅動技術，采用高精度、高剛度的諧波減速機，具有良好的低速穩(wěn)定性和高速動態(tài)響應性[7]。機器人在工作過程中會產生振動，為研究其振動機理，準備對其進行振動與模態(tài)分析，進而對其使用過程產生的振動給出合理解釋[8-11]。

目前，國內外研究模態(tài)特性的方法有很多，常見的有理論分析法、有限元仿真、實驗模態(tài)分析等。時兆義等[12]對下肢外骨骼大腿機器人大腿進行了模態(tài)有限元分析，得到了大腿板的前四階段固有頻率和相應振幅。唐俊杰等[13]對含間隙可控式碼垛機器人開展了動力學特性研究，經(jīng)模態(tài)分析后得出了運動副間隙對固有頻率和振動發(fā)散趨勢的影響，針對現(xiàn)有問題提出了優(yōu)化方案，進行優(yōu)化設計后改善了其動力學特性。Ando等[14]提出了一種新型深海檢測的機器人，利用模態(tài)實驗測試獲取了機器人的模態(tài)參數(shù)，根據(jù)測試結果分析其動力學特性。孫晨光等[15]選取了順應性裝配機器人的大臂，采用模態(tài)分析與拓撲優(yōu)化相結合的方法對其進行優(yōu)化，使優(yōu)化后的機器人提高動力學性能的同時實現(xiàn)了輕量化。

在本文中，針對機器人某一固定位姿，結合模態(tài)基本理論，采用有限元仿真與錘擊實驗測試法相結合的方法對其進行模態(tài)分析。根據(jù)模態(tài)仿真分析與模態(tài)實驗，得到了機器人在固定位姿下的前6階模態(tài)振型與固有頻率，對比仿真與實驗結果，兩者具有較高的擬合度，進而驗證了三維建模與模態(tài)有限元分析的正確性。最后，根據(jù)實驗與仿真結果，討論了機器人動力學特性，結果顯示了機器人具有良好的剛性和穩(wěn)定性。

1 機器人本體描述及模型建立

本文以自主研發(fā)的型號HW700機器人為研究對象，該機器人具有6個自由活動關節(jié)，串聯(lián)裝配。本體主要由底座、腰身、大臂、小臂關節(jié)、小臂、腕部以及末端執(zhí)行器等構成。該機器人靈活度高，到達范圍廣，結構緊湊，管線內置，布局簡單，對外界干涉小，可靠性高，可以在狹小空間靈活進行作業(yè)，可用于打磨、拋光、裝配、搬運等低負載作業(yè)，采用EtherCAT總線型電機，重復定位精度±0.03mm。機器人本體質量約50kg，額定負載6kg，最大工作半徑不低于700mm。機器人本體如圖1所示。

圖1 機器人本體

2 模態(tài)分析基本理論

模態(tài)分析是一種將振動理論應用于實踐的分析方法，其目的是對機構進行動力學特性分析[16]。對于任意一個n自由度線性機械結構系統(tǒng)，其振動方程可以如下表示：

式(1)中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；f(t)為外部激勵；x(t)為位移響應向量。

式(1)的拉氏變化為：

系統(tǒng)響應記為：

其中H(s)為位移傳遞函數(shù)矩陣。在模態(tài)理論中，H(s)可寫為：

H(s)為對稱矩陣，其第c行第r列元素可表示為：

式(5)和式(6)中：φci、φri為第i階振型中的第c行第r列元素；與φci共軛；與φri共軛；si為頻率；ki為模態(tài)剛度；mi為模態(tài)質量。

3 模態(tài)仿真分析

有限元法是將多種思想結合應用的數(shù)值計算方法，它可以將無限自由度問題離散為有限自由度問題，并依靠計算機來輔助實現(xiàn)數(shù)值求解，現(xiàn)已廣泛應用于各個領域。因此，本文借助ANSYS Workbench對機器人進行模態(tài)分析，根據(jù)機器人本體結構，利用SolidWorks建立機器人的三維模型，關節(jié)裝配完成后，選取機器人位姿一進行模態(tài)分析，位姿一如圖2所示。

圖2 機器人位姿一

3.1 三維模型的簡化

由于機器人本體模型復雜，ANSYS Workbench建模功能具有一定的局限性，為了最大程度還原機器人結構，故采用SolidWorks進行三維建模。為有效提高有限元計算效率，需機器人結構中對結果影響不大的特征和部件予以忽略，從而提高網(wǎng)格劃分質量和計算精度，簡化后的模型如圖3所示。

圖3 機器人簡化模型

3.2 模態(tài)仿真前處理

模態(tài)仿真分析前處理流程如圖4所示。

圖4 前處理流程圖

在ANSYS Workbench用戶主界面中選擇預應力模態(tài)分析，將機器人位姿一模型導入ANSYS Workbench中，定義部件材料為結構鋼，屈服強度為250MPa，密度為7.85g/cm3，泊松比為0.269，彈性模量為206000MPa。打開模型后，在機器人底座與地面之間添加固定約束，并賦予其重力屬性。為保證計算效率和精度，網(wǎng)格劃分采用四面體單元，產生了224711個節(jié)點和146934個單元，劃分結果如圖5所示。

圖5 機器人網(wǎng)格劃分結果圖

3.3 仿真結果與分析

因HW700機器人具有6個自由活動關節(jié)，故只需分析前6階模態(tài)即可。因受篇幅所限，這里只展示機器人在位姿一下的前3階振型圖，如圖6所示，前6階固有頻率如表1所示。

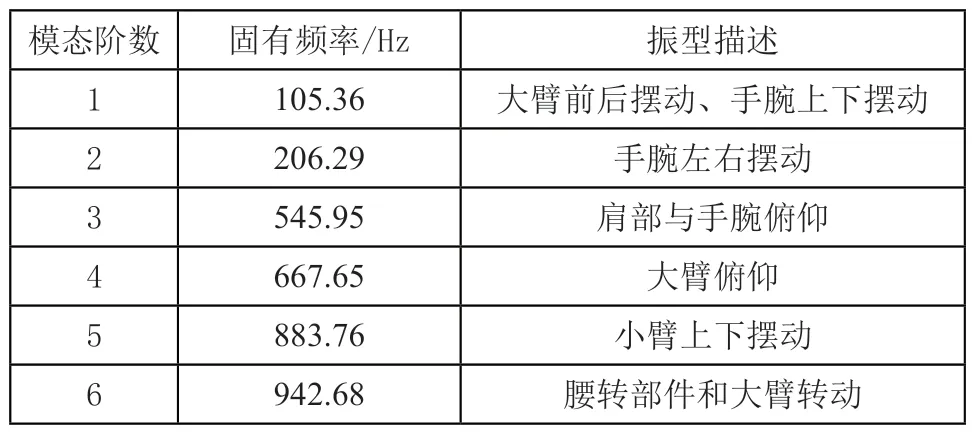
表1 固有頻率

圖6 機器人在位姿一下的振型圖

分析圖6和表1可知，在模態(tài)仿真中，機器人的最低階固有頻率為105.36Hz，振型主要表現(xiàn)為大臂前后擺動、手腕上下擺動；第2階固有頻率為206.29Hz，振型主要表現(xiàn)為手腕左右擺動；第3階固有頻率為545.95Hz，振型主要表現(xiàn)為肩部與手腕俯仰；第4階固有頻率為667.65Hz，振型主要表現(xiàn)為大臂俯仰；第5階固有頻率為883.76Hz，振型主要表現(xiàn)為小臂上下擺動；第6階固有頻率為942.68Hz，振型主要表現(xiàn)為腰轉部件和大臂轉動。

4 模態(tài)實驗分析

為進一步準確掌握機器人模態(tài)參數(shù)與特征，在現(xiàn)有實驗條件下自主設計并搭建了模態(tài)實驗測試平臺，完成信號采集和信號分析任務為實驗的兩個基任務。在實驗過程中，利用力錘依次敲擊機器人各個布點以產生激勵信號，加速度傳感器進行信號響應與輸出，LMS數(shù)據(jù)分析系統(tǒng)儀進行信號采集，安裝在計算機LMS Test.Lab 17軟件對采集的信號進行識別與分析。模態(tài)實驗流程圖如圖7所示。

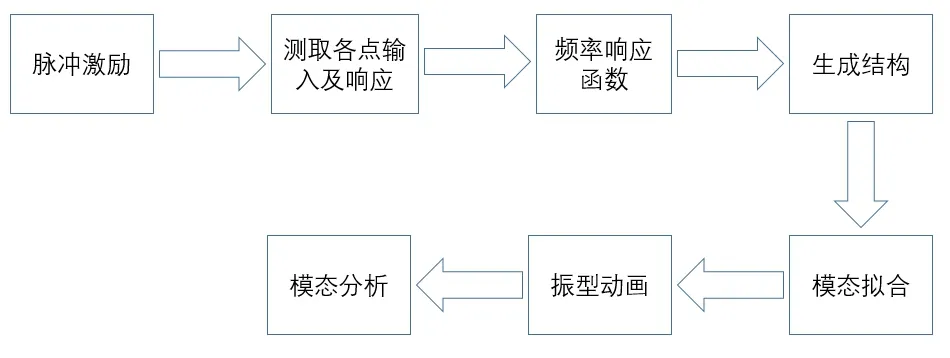
圖7 模態(tài)實驗流程圖

4.1 實驗目的及條件

實驗目的：

驗證三維建模和模態(tài)仿真的正確性；

進一步準確了解機器人的振動特性。

實驗對象：HW700型六自由度串聯(lián)機器人。

實驗儀器：LMS數(shù)據(jù)分析系統(tǒng)儀、力錘、三個單向加速度傳感器、一個三向加速度傳感器、計算機。

4.2 實驗方案和過程

建立模型：機器人在位姿一下，根據(jù)其本體實際結構，在各連桿上布置均勻且數(shù)目合適的測點，將其簡化為如圖8所示的線框圖。在LMS Test.Lab 17軟件中建立模型時，一共布置了68個結構特征測點，點的位置和順序分別為移步敲擊的位置和順序。

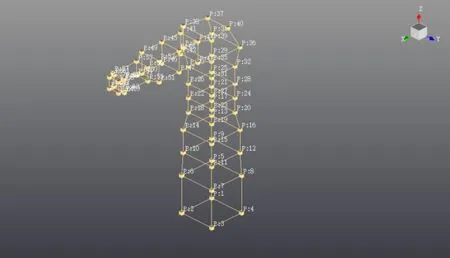
圖8 機器人測點分布圖

傳感器的布置及測試連接：分別在點18、31、49處固定布置一個單向加速度傳感器，在點65處固定放置一個三向加速度傳感器。完成傳感器布置后，進而完成數(shù)采前端連接，振動測試連接如圖9所示。

圖9 振動測試連接圖

通道設置：實驗測試一共含7條通道，其中，Input1為力錘輸入通道，將其定義為參考通道；三向加速度傳感器含3個通道，分別為Input2、Input3、Input4；Input5、Input6、Input7分別為布置在點18、31、49處的單向加速度傳感器對應的通道。在Channel1的Groupld中定義力錘和加速度計的測量類型為vibration。在Direction中設置測點所測振動的方向，參考模型坐標系后設定Input2的方向為+Z；Input3的方向為-Y；Input4的方向為+X；Input5的方向為+Y；Input6的方向為-X；Input7的方向為+Y。7個通道的傳感器類型均為ICP，其中，力錘的靈敏度值為102.9mv/g；三向加速度在X、Y、Z上靈敏度值分別為23.73mv/g、24.38mv/g、25.29mv/g；三個單向加速度傳感器型號一致，靈敏度值均為100mv/g。

錘擊示波：定義波的帶寬為4096Hz，頻率分辨率為4Hz；隨后在進行通道增益的過程中，對機器人進行了3次均勻力度大小的錘擊，為此，保證系統(tǒng)能確定一個合適的量程范圍以得到更精確的結果。

錘擊設置：首先是進行觸發(fā)級設置，用均勻大小力錘擊機器人，可以看見脈沖后點擊應用建議值確定觸發(fā)設置，其中，輸入量程為10V，觸發(fā)電平為0.0124V，預觸發(fā)極時間為0.009s。其次是進行帶寬設置，用均勻大小力對機器人進行兩次錘擊后確定帶寬選取值為1600Hz。隨后是進行加窗設置，主要步驟為點擊測量，錘擊機器人，停止測量，停止測量后選用信號衰退至100%的軟件建議值。最后是進行驅動點設置，因該測量方案含6條加速度傳感器通道，因此，設置了6個最佳激勵點，每個最佳激勵點的確定分別進行了兩次錘擊。

測量：設置每個布點測量的平均次數(shù)為2次，每一次均為自動接受。為達到良好的實驗效果，設置了自動拒絕過載激勵和雙擊。完成所有設置后即可進行測量，主要步驟為：選擇激勵點（為擬合每個關節(jié)的實際旋轉方向，需依次設定每個點對應的敲擊方向）；點擊Start開始；接受測量結果；循環(huán)以上操作進行逐點測量。機器人模態(tài)實驗測試如圖10所示。

圖10 機器人模態(tài)實驗測試圖

4.3 實驗結果與分析

實驗數(shù)據(jù)采集完成后，選取所有的模態(tài)數(shù)據(jù)進行分析，分析頻段選擇0～1600Hz，調整模態(tài)階數(shù)為256，在有明顯峰極的的地方選取極點，和仿真一樣選取6個極點，機器人穩(wěn)態(tài)圖如圖11所示，固有頻率如表2所示。

表2 固有頻率

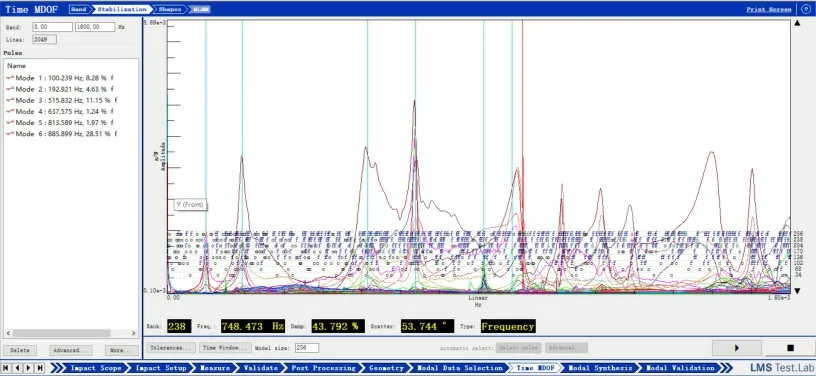
圖11 機器人穩(wěn)態(tài)圖

分析圖11和表2可知，在實驗中機器人的最低階固有頻率為100.239Hz；第2階固有頻率為192.921Hz；第3階固有頻率為515.832Hz；第4階固有頻率為637.575Hz；第5階固有頻率為813.589Hz；第6階固有頻率為885.899Hz。其中，第1、3、4、6階模態(tài)振型結果與仿真略有差異，第2、5階模態(tài)振型與仿真結果完全一致。

4.4 仿真與實驗結果對比分析

結合以上仿真與實驗結果，可對機器人模態(tài)參數(shù)進行對比分析，參數(shù)對比如圖12所示。

圖12 仿真與實驗模態(tài)參數(shù)對比圖

分析表3可知，機器人在位姿一下，仿真與實驗所獲得的機器人前6階模態(tài)參數(shù)走勢大致相同，兩者具有較高的擬合度，可作為相互補充。仿真測得的最低階固有頻率較于實驗所測的誤差率為5.1%；仿真測得的第2階固有頻率較于實驗所測的誤差率為6.9%；仿真測得的第3階固有頻率較于實驗所測的誤差率為5.8%；仿真測得的第4階固有頻率較于實驗所測的誤差率為4.7%；仿真測得的第5階固有頻率較于實驗所測的誤差率為8.6%；仿真測得的第6階固有頻率較于實驗所測的誤差率為6.4%；結果誤差在可容范圍內，實驗結果驗證了三維建模與模態(tài)有限元分析的正確性。在實驗結果中，機器人基頻為105.36Hz，達到了較高水平，顯示出機器人整機具有良好的剛性和穩(wěn)定性。利用仿真與實驗的手段相結合，有效改善了模態(tài)參數(shù)獲取繁雜的問題，準確掌握機器人的振動特性為今后對機器人進行振動故障診斷以及結構優(yōu)化設計提供了重要依據(jù)。

5 結語

在本文工作中，結合機器人本體結構，利用SolidWorks建立機器人的三維模型，為提高模態(tài)有限元分析效率，對機器人進行了合理簡化，進行關節(jié)裝配后，將其調整為位姿一的姿態(tài)。針對機器人在位姿一下，本文將有限元仿真與錘擊實驗測試相結合的方法對其進行了模態(tài)分析。通過模態(tài)仿真與實驗，得到了機器人前6階模態(tài)振型與固有頻率。在實驗結果中，機器人的基頻為105.36 Hz，達到了較高水平，顯示出機器人整機具有良好的剛性和穩(wěn)定性。對比分析仿真與實驗結果，結果誤差率最高為8.6%，兩者具有較高的擬合度，可作為相互補充，有效驗證了三維建模的正確性，并改善了機器人模態(tài)參數(shù)獲取繁雜的問題。準確獲取機器人參數(shù)，明確機器人整體動態(tài)特性，合理評價機器人工作性能，對今后對機器人進行振動故障診斷以及結構優(yōu)化設計研究具有重要意義。