準零剛度驅動式壓電低頻振動能量采集方法1)

陳婷婷 王 凱,,2) 成 利 周加喜,)

* (湖南大學機械與運載工程學院,長沙 410082)

? (香港理工大學機械工程系,香港 999077)

引言

壓電材料因其可實現機械能和電能互換的特性,受到工程應用及科研人員的重視,被廣泛應用于健康監測、計量元件的傳感結構及損傷探測等領域[1-4].從環境振動、機械振動或者人體運動中采集能量,將其轉化為電能可以極大滿足傳感器自主供電的環保要求和經濟需求[5-6].近些年來由于微電子及物聯網的高速發展,對μW/mW 級的電能應用場景逐漸增多,因此將壓電材料用于能量俘獲并應用于傳感器自供能設計也得到極大的關注[7-10].壓電俘能材料根據外力加載方向的不同,可以分為d33 和d31 兩種模式,d33 模式是施加的外力方向平行于壓電材料極化方向;而d31 模式是施加的外力方向垂直于壓電材料極化方向.其中,d33 模式更適用于高頻能量俘獲,而d31 模式一般由組合梁的方式呈現,更適合于中低頻段能量俘獲[11],同時后者俘能結構因可設計性更強,得到更加廣泛的研究.

懸臂梁結構是最常見的壓電俘能方式,Sun 等[12]綜述了超低頻振動能量采集的研究情況,其中懸臂梁式的壓電能量采集結構在文中占了很重要的篇幅.傳統的線性懸臂梁壓電俘能器利用結構共振獲取高效振動能量俘獲,但其工作頻帶窄,且必須要匹配到其共振頻率時才能實現高效俘能.因此,簡單的線性懸臂梁壓電俘能裝置因其低頻振動能量轉化效率較低、俘能頻帶較窄而難以勝任復雜環境的能量俘獲.為解決線性懸臂梁壓電俘能方法的局限性,研究人員設計了頻率可調[13-14]的壓電能量采集器來增加其實用性.為拓寬壓電俘能器的有效工作頻帶,研究人員在梁上加裝多個質量塊構造多模態懸臂梁[15-17],實現了振動能量高效俘獲頻帶的成倍拓寬.在提高能量轉化效率方面,利用多段懸臂梁協同工作,可以明顯提升能量采集系統的俘能效率[18].此外,Zou 等[19]構建了機械調制能量采集方法體系,從激勵形式轉換、升頻與力和運動放大等3 方面提高機械能量采集系統性能.但是,對于傳統線性共振型壓電能量采集系統而言,面臨著承載能力和低固有頻率之間的矛盾,難以實現低頻,甚至超低頻振動能量高效俘獲.

為克服線性共振型壓電能量采集方法在低頻振動能量高效俘獲方面的局限性,研究人員發展了非線性多穩態振動能量俘獲方法,并迅速獲得極大的關注.例如,Liao 等[20]利用流體誘導振動設計了一種雙穩態壓電能量采集器(BS-PEH),其研究結果表明所提出的振動能量采集方法能夠明顯提高能量采集功率密度.Feng 等[21]提出了一種仿生雙穩態壓電能量采集器,并證明了其在寬頻振動能量俘獲方面的優勢.Wang 等[22]也設計了一種基于彈簧的雙穩態能量收集器(SBEH),并證明了其從不同低頻振動環境中俘能的能力.Zhou 等[23]受鳥類雙翅飛行機理的啟發,提出一種新型仿生雙翅壓電能量采集器(BDEH),用于采集低頻振動能量.多穩態結構由于其運動形式更加豐富,將其與壓電材料結合用于振動能量俘獲受到很多學者的關注和研究.Fang 等[24]綜述了多穩態效應特點及其在能量采集等多方面的應用.以三穩態結構為例,其結構有3 個對稱的勢能阱,且勢能阱的深度要比雙穩態淺,寬度要比雙穩態寬,因此能實現較低強度下更寬頻的振動能量采集.Zhou 等[25]探究了非對稱的三穩態能量采集器的動力學行為以期能提高三穩態壓電俘能器的俘能效果.聶欣等[26]研究了窄帶隨機激勵下三穩態壓電俘能器,并且通過實驗驗證了三穩態壓電俘能器在隨機振動能量俘獲方面的優越性.

但是,不論是雙穩態還是三穩態等多穩態結構,都難以擺脫勢能阱和勢壘的束縛,即只有當系統跨越勢壘時才能產生較大的動力學響應幅值,從而實現振動能量的高效俘獲.為克服勢壘對低頻振動能量高效俘獲的限制,Chen 等[27]設計了一種有自減勢壘效應的雙穩態能量收集器,采用彈簧磁振子對懸臂梁進行雙向糾偏,使勢壘在返回平衡位置時動態降低;而當遠離平衡位置時,勢能增強,實現了16.17 Hz的超寬高效率振動能量采集頻帶.鄭友成等[28]設計了一種線性放大與非線性磁力復合增強的三穩態壓電俘能裝置,可以減小低能軌道到高能軌道所需的激發能量,同時還拓寬了阱間運動的頻率范圍.

雖然研究人員在線性共振型壓電能量采集方法和非線性多穩態壓電能量采集方法方面進行了諸多研究,但要想實現低頻小振幅振動能量高效采集,尤其是在10 Hz 以下的超低頻俘能,還存在一定困難.鑒于此,本文提出了一種準零剛度驅動式壓電能量采集裝置.其中,壓電復合梁結合連桿形成負剛度機構,并在靜平衡位置處與正剛度相互抵消,使能量采集系統實現準零剛度特性.本文首先通過能量法求出機電耦合方程,并通過多項式對系統非線性回復力進行擬合,結合諧波平衡法,推導動力學響應與電學輸出的解析幅頻響應方程.制備實驗樣機,搭建了實驗測試平臺,驗證了理論分析結果.本研究有望為低頻小振幅振動能量采集提供新思路.

1 模型設計及力學分析

1.1 模型及能量采集單元力學分析

圖1 展示了準零剛度驅動式壓電俘能裝置模型圖,整個裝置由一個底板、4 根導柱、兩根壓電復合梁和一個線性彈簧組成.壓電俘能裝置的結構參數如圖1 所示,其中基梁長113 mm,壓電薄膜長85 mm,基梁和壓電膜的寬度均為10 mm,連桿的長度b=25 mm.當壓電復合梁處于自由狀態時,連桿傾斜,所對應的水平距離a=17 mm.當將附加質量置于準零剛度俘能系統時,系統處于靜平衡位置(連桿處于水平位置),壓電復合梁具有最大跨中撓度.此時,壓電復合梁同連桿共同組成俘能系統的負剛度機構,抵消正剛度彈簧的剛度值.當系統受到外部激勵時,附加質量向上或向下移動,當附加質量到達最高或者最低點后再回到平衡位置時,系統完成了半個運動周期,此時壓電復合梁完成一個運動周期.因此,準零剛度驅動式能量采集系統的電學輸出頻率是準零剛度系統動力學響應頻率的兩倍.

圖1 俘能裝置結構模型圖Fig.1 Structure model diagram of energy harvesting device

對壓電復合梁進行力學分析,其模型示意圖以及局部坐標系如圖2 所示.圖2(a)中L表示基梁的長度,Lp表示壓電膜的長度,H(t)表示壓電復合梁的跨中撓度.其中,黑色虛線表示復合梁在受集中力作用后,發生彎曲變形的形狀.圖2(b)展示了壓電復合梁的橫截面圖,其中db和hb分別代表梁的寬度和厚度,dp和hp分別代表壓電膜的寬度和厚度.

圖2 復合梁模型及其截面圖Fig.2 Composite beam model and its cross section

研究人員發現,對于受跨中集中力作用的簡支梁而言,其撓曲線可以用半正弦波函數進行近似描述[29-30],即復合梁的撓曲線方程可表示為

式中,H(t)是復合梁的跨中撓度,其表達式為

其中X(t)表示準零剛度系統的位移響應.根據復合梁的撓曲線方程,梁的應變與應力方程可由系統動力學響應表示為

其中Yb表示梁的楊氏模量.假設壓電薄膜的應變等于其與基體梁結合處基體梁表面的應變,則壓電薄膜的應變可以表示為

對于本文所研究的壓電片,其簡化本構方程可寫為[31]

式中,σp是壓電膜的應力,Yp是壓電膜的楊氏模量,e31為壓電片的應力常數,E3為電場強度,D3為電位移,η33為恒定應變下的介電常數.在均勻電場強度下,電場強度E3和電壓之間的關系可表達為

則壓電薄膜輸出的電流為

式中Ap是壓電膜的橫截面積.將式(5)、式(7)和式(8)代入式(9),電流方程可表示為

其中(t)和(t)分別表示壓電薄膜輸出電壓以及能量采集系統位移響應對時間的導數,若將壓電薄膜的等效電容引入式(10),即

則壓電薄膜的輸出電壓可改寫為

若假設壓電復合梁在其跨中有虛位移 δH,基體梁與壓電薄膜的虛應變分別為 δεb與 δεp,此時壓電復合梁的虛應變能可表示為

式中,Ab是基體梁的橫截面積,將式(3)、式(6)和式(8)代入到式(13),復合梁的整體虛應變能可表示為

當在壓電復合梁跨中處作用一定位移后,假設壓電復合梁提供的回復力為Fmid,根據虛功原理,復合梁的虛應變能也可表示為

將式(14)代入到式(15),則集中力Fmid可以表示為

顯然,式(16)是一個機電耦合方程,若引入機電耦合系數

以及力學參數

壓電復合梁的電學回路方程可以表示為

顯然,當給定系統的動力學響應X(t)后,即可由式(19)與式(20)獲得壓電復合梁的跨中回復力以及能量轉化單元的電學回路方程.

1.2 系統的動力學分析

對準零剛度驅動式壓電能量采集系統而言,當系統在豎直方向上運動位移為X(t)時,其系統回復力可以表示為

式中,K表示豎直彈簧的剛度,θ表達當系統偏離靜平衡位置X后連桿與水平線的夾角.將式(21)對位移X求導,則準零剛度驅動式壓電能量采集系統的非線性剛度可以表示為

為獲得準零剛度特性,假設在靜平衡位置處能量采集器的剛度值等于0,此時系統的響應位移為0,進而壓電薄膜的輸出電壓也為0,即

由式(23)可以得出,系統的準零剛度條件為

將式(24)代入式(21),則具有準零剛度特性的壓電能量采集器回復力表達式可以表示為

當給定系統的動力學響應以及電學響應后,由式(25)即可獲得系統的回復力值.在基礎激勵U=U0cos(ωt)(式 中U0表示位移幅值,ω表示頻率)作用下,能量采集器的機電耦合動力學方程為

式中,M表示能量采集器質量塊的質量,C表示線性黏性阻尼系數.

由于兩根壓電復合梁始終處于相同的變形狀態,所以兩片壓電薄膜具有相同的電學輸出.若考慮外接電阻R,則由歐姆定律可知能量采集器的電學回路方程為

將式(27)代入式(20),則能量采集器的第2 個機電耦合方程可以表示為

以及

對于給定的外激勵頻率和外激勵幅值,通過求解式(29)和式(30)即可獲得能量采集器的動力學響應和電學輸出.

1.3 機電響應的解析表達

為獲得準零剛度驅動式壓電能量采集系統動力學響應與電學輸出的解析表達式,首先給出其在靜平衡位置處的回復力表達式

對回復力在靜平衡位置處進行三階泰勒展開,即

對于準零剛度系統而言,其剛度值在靜平衡位置處等于0,即 κ1=0.

同時將機電耦合方程中機電耦合系數

在靜平衡位置處用泰勒級數展開,其三階展開表達式為

準零剛度驅動式壓電能量采集系統的回復力和機電耦合系數的原始表達式和多項式擬合對比如圖3 所示,其中黑色和紅色實線分別代表由精確表達式獲得的回復力和機電耦合系數曲線,而藍色米字和黃色星星分別表示由多項式擬合得到的回復力和機電耦合系數曲線.顯然,無論是回復力還是機電耦合系數,其由精確表達式獲得的曲線能夠與由多項式擬合表達式獲得的曲線在設計使用范圍內較好吻合,換言之,3 階泰勒展開表達式能夠表征能量采集系統的回復力和機電耦合特性,能夠用于推導機電響應的解析表達式.

圖3 回復力和機電耦合系數的原函數和擬合函數圖(γ=1.562 5,θ=0.21,A=0.17,B=0.25)Fig.3 The original function and polynomial approximation diagram of restoring force and electromechanical coupling coefficient (γ=1.562 5,θ=0.21,A=0.17,B=0.25)

將式(32)與式(35)代入式(29)與式(30),準零剛度驅動式壓電能量采集系統的機電耦合動力學方程可以改寫為

從能量俘獲單元的俘能原理分析可知,準零剛度驅動式壓電能量采集系統的位移響應頻率等于激勵頻率,而電學響應頻率是外激勵頻率的二倍.因此,假設系統的位移響應和電學響應的表達式為

其中 ?1和 ?2分別表示力學響應和電學響應的相位.將式(38)代入式(36),并令左右兩邊相同諧波的系數相等,可以得到

將式(38)代入到式(37)中,使兩邊諧波相等的各項系數和相等,可以得到

結合式(41)可以得出 cos(2?1-?2)和 sin(2?1-?2)異號,結合式(4 2)可以得到 cos(2?1-?2)>0,sin(2?1-?2)<0.同時將式cos2(2?1-?2)=1-sin2(2?1-?2)代入到式(41),可以解得

將式(43)、式(44)代入到式(42)中,可以得到

將式(43)～式(45)代入到式(39)和式(40)中,可得到準零剛度驅動式能量采集系統的幅頻響應方程

此外,由式(45)可得出A12和B1的關系

將式(47)代入式(46),即可獲得準零剛度驅動式能量采集系統電學輸出的幅頻響應方程.對于給定的外激勵頻率與幅值,由力學與電學幅頻響應方程即可獲得系統的動力學響應與電學輸出,并評估系統在低頻振動能量采集方面的優勢.

2 結果比對與參數分析

2.1 數值結果與解析解結果比對

準零剛度驅動式能量采集系統的位移幅頻響應曲線與電學輸出幅頻響應曲線如圖4 所示,其中黑色實線表示由解析表達式獲得的結果,紅色正六邊形表示數值解正向掃頻結果,藍色十字表示數值解逆向掃頻結果.如圖4(a)所示,準零剛度驅動式能量采集系統的解析位移幅頻響應曲線與通過直接求解系統機電耦合動力學方程獲得的數值位移幅頻響應曲線具有較高的一致性: 在下跳頻率之前的低頻范圍以及在下跳頻率之后的高頻范圍內,由解析表達式獲得的系統動力學幅頻響應曲線與由數值求解系統機電耦合方程獲得的數值解完全一致,曲線相互重疊;數值幅頻響應曲線的下跳頻率高于解析幅頻響應曲線的下跳頻率,且數值幅頻響應曲線在下跳頻率處所對應的位移響應幅值略高于解析幅頻響應曲線下跳頻率所對應的幅值,主要原因為當使用諧波平衡法推導系統機電響應時對系統的回復力與機電耦合力進行多項式擬合,產生擬合誤差.此外,在推導系統機電響應的解析表達式時,舍去了機電響應的高階諧波項,導致由解析表達式獲得的系統響應幅值略小于由求解原始機電耦合方程所獲得的數值結果.

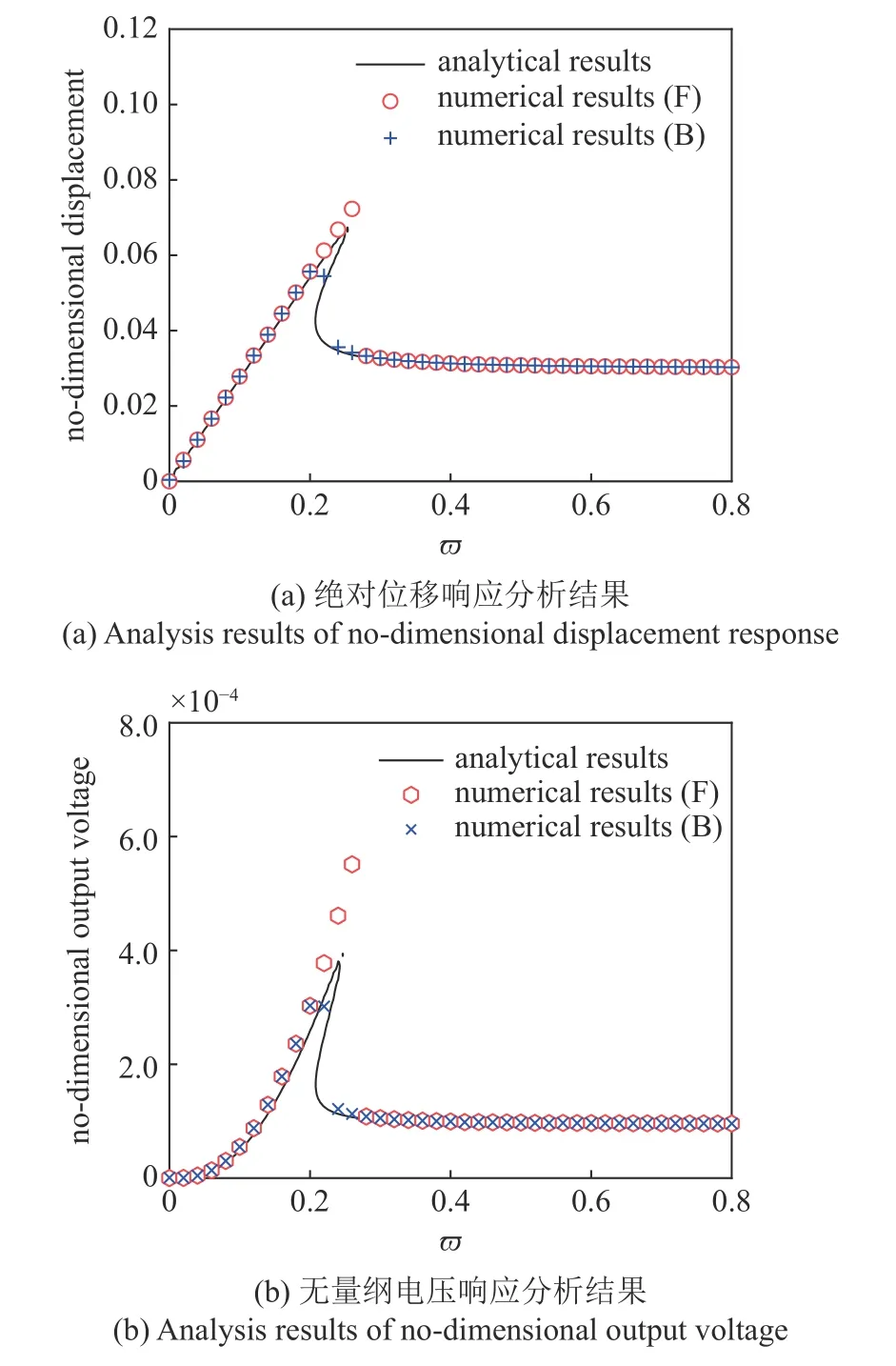
圖4 數值結果與解析解結果對比(γ=1.562 5,ζ=0.055,ρ=2,θ=0.21,u0=0.03)Fig.4 Comparison of numerical results and analytical results(γ=1.562 5,ζ=0.055,ρ=2,θ=0.21,u0=0.03)

圖4(b)為準零剛度驅動式能量采集系統輸出電壓的幅頻響應曲線.顯然,輸出電壓的幅頻響應曲線與如圖4(a)所示的位移幅頻響應曲線具有一致性,即在低于下跳頻率與高于下跳頻率的頻率范圍內,輸出電壓的數值結果與由解析表達式獲得的理論結果相互吻合,但是數值下跳頻率略高于解析下跳頻率,且數值下跳頻率對應的電壓幅值略高于解析下跳頻率對應的電壓幅值.實際上,電學響應與位移響應的一致性主要是因為準零剛度驅動式能量采集系統的能量轉化單元(壓電復合梁)由準零剛度系統進行驅動,其形變與系統的位移響應嚴格相關.換句話說,當準零剛度系統的動力學響應幅值較大時,壓電復合梁產生較大的跨中撓度,進而使壓電薄膜產生較大應變并輸出較大電壓.綜上所述,由諧波平衡法獲得的解析表達式能夠用于計算準零剛度驅動式能量采集系統的動力學響應與電學輸出,以快速評估系統的機電性能.

2.2 參數分析

2.2.1 阻尼比的影響

本文所提出的準零剛度驅動式能量采集系統不可避免地存在著機械摩擦與結構阻尼.本節通過改變系統阻尼比,并結合動力學響應與電學輸出的解析表達式,定性分析機械摩擦與結構阻尼對系統動力學響應與電學輸出特性的影響,如圖5 所示.顯然,當阻尼比從0.045 增大至0.065 時,準零剛度驅動式能量采集系統在外激勵頻率小于下跳頻率的頻率范圍內動力學響應幅值逐漸減小,下跳頻率向低頻移動,具有大位移響應幅值的頻帶變窄,如圖5(a)所示.此外,當阻尼比增大至0.06 時,準零剛度驅動式能量采集系統位移幅頻響應曲線的下跳現象消失;當阻尼比增大至0.065 時,準零剛度驅動式能量采集系統位移幅頻響應曲線無明顯共振現象.需要注意的是,當外激勵頻率大于下跳頻率時,無論阻尼系數如何變化,準零剛度驅動式能量采集系統的相對位移響應幅值基本等于外激勵幅值,即基礎激勵被準零剛度系統隔離,能量采集系統的振動幅值明顯減小.

圖5 阻尼對位移及電壓響應的影響(γ=1.562 5,ρ=2,θ=0.21,u0=0.03)Fig.5 Influence of damping on displacement and voltage response(γ=1.562 5,ρ=2,θ=0.21,u0=0.03)

系統阻尼對準零剛度驅動式能量采集系統無量綱輸出電壓幅頻響應曲線的影響如圖5(b)所示.同位移幅頻響應曲線一致,當阻尼系數由0.045 增大至0.065 時,輸出電壓幅值在下跳頻率之前的頻率范圍內明顯減小,電壓幅頻響應曲線的下跳頻率向低頻范圍內移動,準零剛度驅動式能量采集系統在低頻范圍內的能量采集效率降低,高效能量采集頻帶變窄.當阻尼比增大至0.06 時,無量綱輸出電壓幅頻響應曲線無明顯共振現象,且隨外激勵頻率增加,輸出電壓保持不變.綜上所述,對于準零剛度驅動式能量采集系統而言,減小阻尼比有利于拓寬高效能量采集頻帶并提高振動能量轉化效率.

2.2.2 激勵幅值的影響

圖6 表示當阻尼比等于0.055 時激勵幅值對動力學響應和電學輸出幅頻響應曲線的影響,其中紅色空心球,藍色星星,玫紅色四邊形和綠色實心球形分別代表無量綱激勵幅值為0.02,0.025,0.03 和0.035 時對應的動力學和電學響應.從圖6(a)中可以看出,隨著激勵幅值的減小,準零剛度驅動式能量采集系統位移幅頻響應曲線的下跳頻率向低頻移動,且下跳頻率對應的位移幅值明顯增大.當無量綱外激勵幅值減小至0.03 時,位移幅頻響應曲線的下跳現象消失;當外激勵幅值進一步降低時,系統再無明顯共振現象,且在高頻區域內位移響應幅值隨外激勵頻率的增加而保持不變.

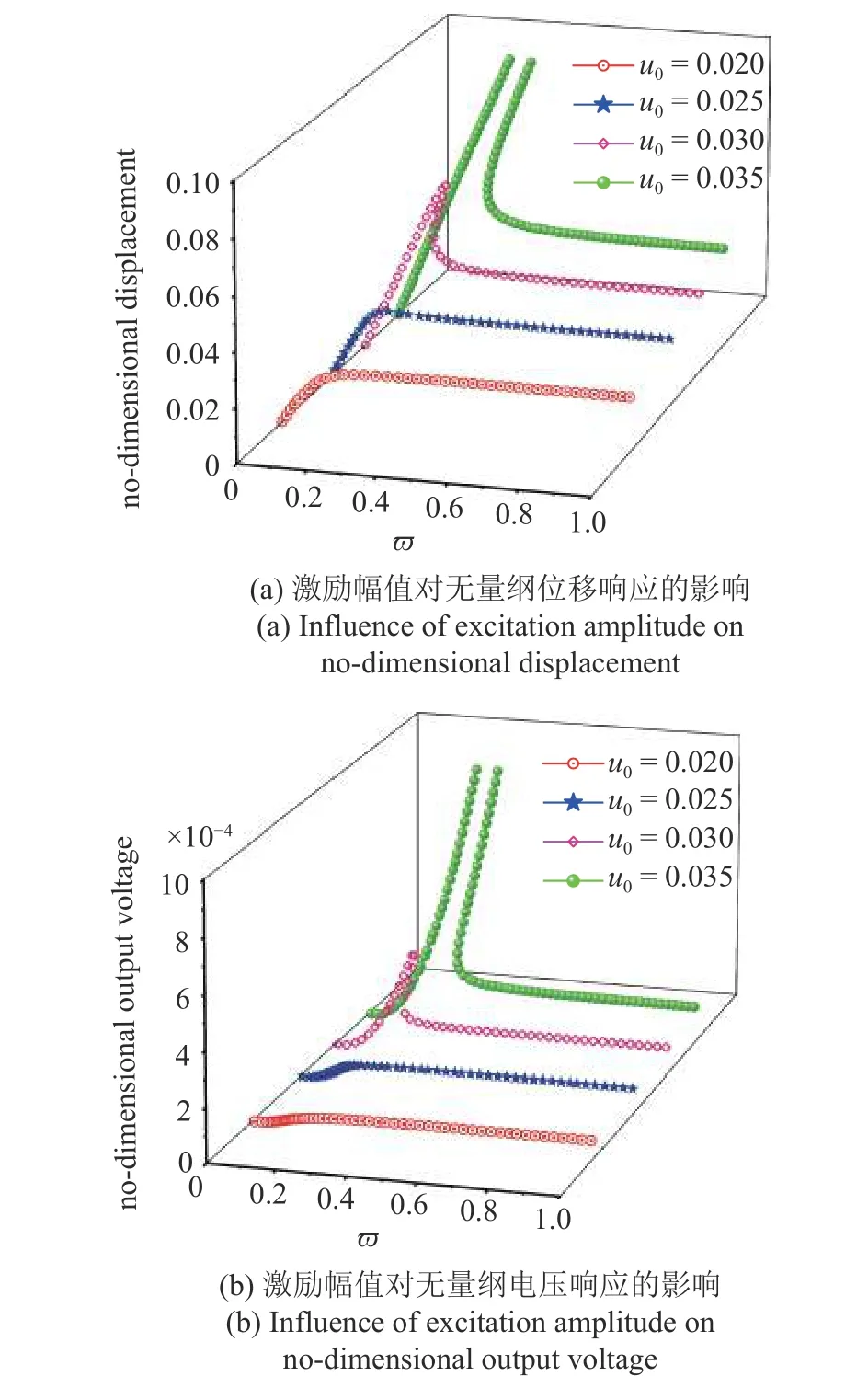
圖6 激勵幅值對位移和輸出電壓響應的影響(γ=1.562 5,ζ=0.055,ρ=2,θ=0.21)Fig.6 Influence of excitation amplitude on displacement and output voltage (γ=1.562 5,ζ=0.055,ρ=2,θ=0.21)

外激勵幅值對準零剛度驅動式能量采集系統無量綱輸出電壓幅頻響應曲線的影響如圖6(b)所示.因能量轉化單元的運動幅值與準零剛度系統的動力學響應嚴格相關,即壓電薄膜的應變隨系統的運動位移增大而增大,所以外激勵幅值對輸出電壓幅頻響應曲線的影響與對位移幅頻響應曲線的影響完全一致.即,當外激勵幅值增大后,輸出電壓的下跳頻率向高頻區域移動,能量采集系統具有更寬的高效能量轉化頻帶,且在低頻區域內具有更高的輸出電壓.

3 實驗與討論

為驗證機電耦合動力學方程以及動力學與電學響應解析表達式的正確性,結合增材制造技術與數控加工技術,加工制備了準零剛度驅動式能量采集系統樣機,并搭建了實驗測試平臺,實驗樣機中壓電薄膜的材料與幾何參數如表1 所示,準零剛度驅動式能量采集器的幾何參數見圖1.

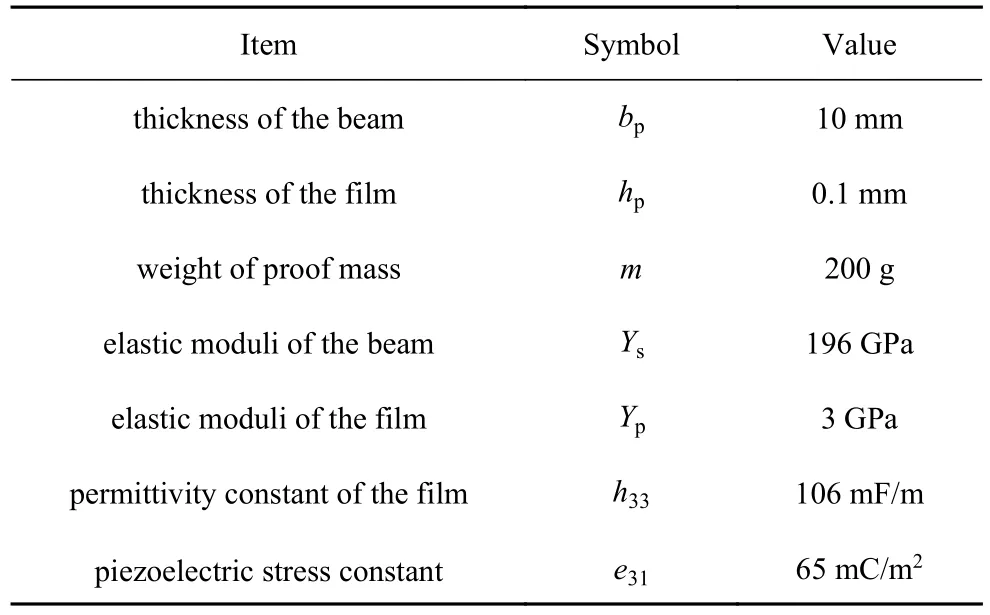
表1 模型的相關物理參數Table 1 Relevant parameters of the prototype

圖7 展示了實驗設備和實驗測試過程.其中,實驗測試平臺主要包括靜電計(吉時利6514)、激光位移傳感器(LTS-200-100)、激振器(JZK-10)、筆記本電腦、信號發生器(VT-9008)和功率放大器(YE5874 A)等.實驗中,準零剛度驅動式能量采集器(即QZSE-PEH)固定在激振器上,激光位移傳感器置于黑色橫梁上且可左右移動,以測試輸入激勵幅值及能量采集系統的位移響應.壓電薄膜通過兩根導線與靜電計相連,以測試能量采集系統在受到外激勵時壓電薄膜的輸出電壓.需要注意的是,因準零剛度驅動式能量采集系統左右兩側壓電復合梁的幾何屬性、材料屬性以及動力學響應均完全一致,僅需測量一片壓電薄膜的輸出電壓即可獲得另外一片壓電薄膜的電學輸出.本次實驗所使用靜電計的內阻為200 TΩ,其數值遠大于一般電阻元件的電阻值,所以由靜電計測試得到的輸出電壓可近似認為是系統開路電壓.實驗測試條件為在激勵頻率0～8 Hz 范圍內進行定幅值正弦激勵,單個頻率點駐留時間為2 min.為消除測試誤差,每組實驗都重復3 次.

圖8 展示了在激勵幅值分別為2 mm,3 mm和3.5 mm 時,準零剛度驅動式能量采集系統的絕對位移幅頻響應曲線和峰值電壓幅頻響應曲線.其中藍色實線,綠色實線和紅色實線分別代表激勵幅值為3.5 mm,3 mm 和2 mm 時系統的輸出.從圖中可以看出,隨著激勵幅值的增大,系統的絕對位移響應逐漸增大.如圖8(b)所示的輸出電壓幅頻響應曲線展示出與系統位移幅頻響應曲線完全一致的趨勢,即隨著外激勵幅值的增加,能量采集系統的輸出電壓逐漸增大,這與通過數值求解系統機電耦合方程獲得的數值幅頻響應曲線以及由解析表達式獲得的解析幅頻響應曲線具有一致性.本文所推導的機電耦合方程以及解析表達式可用于評估能量采集系統的能量采集性能.

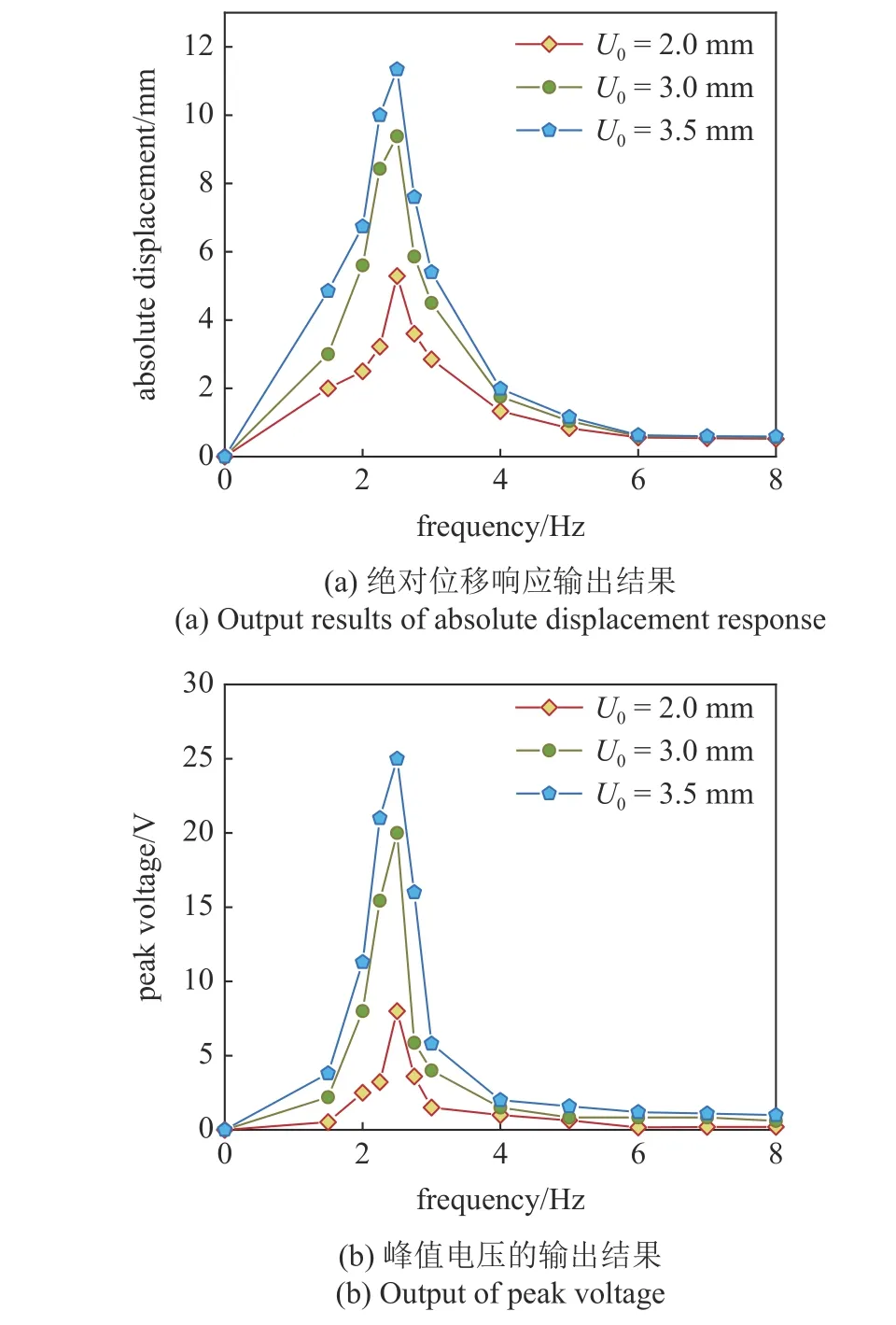
圖8 不同激勵幅值下絕對位移響應與峰值電壓的輸出結果Fig.8 Output results of absolute displacement response and peak voltage under different excitation amplitudes

為進一步觀察位移響應和輸出電壓響應的細節情況,圖9 展示了在2.5 Hz 時絕對位移響應和輸出電壓響應的時域圖.圖9(a)、圖9(b)和圖9(c)分別展示了激勵幅值為2 mm,3 mm 和3.5 mm 時輸入幅值(input)與響應幅值(output)的情況,其中黑色實線表示輸入激勵幅值,紅色、綠色及藍色短點畫線分別表示激勵幅值為2/3/3.5 mm 時位移響應的幅值.顯然,準零剛度驅動式能量采集系統的絕對位移響應具有與輸入激勵完全一致的頻率.激勵幅值越大,對應的輸出響應也越大.圖9(d)展示了激勵幅值為2 mm,3 mm 和3.5 mm 時能量采集系統的開路電壓時域響應曲線,分別用紅色實線、綠色雙畫線、藍色點畫線表示.可以看出隨著激勵幅值的增大,對應的開路電壓響應的值也越大.在激勵幅值等于3.5 mm 時,系統開路電壓峰值達到最大值25 V.需要注意的是,準零剛度驅動式能量采集系統輸出電壓的頻率為基礎激勵頻率以及系統絕對位移響應頻率的兩倍,這與準零剛度驅動式能量采集系統工作原理分析結果一致.此外,當壓電薄膜只受到單邊彎矩且無電荷泄露時,其輸出電壓表現為單方向.文獻[32-33]中給出了解釋,即只有當電壓表的內阻大于臨界有效值時,測得的電壓才能與理論分析中的一致.

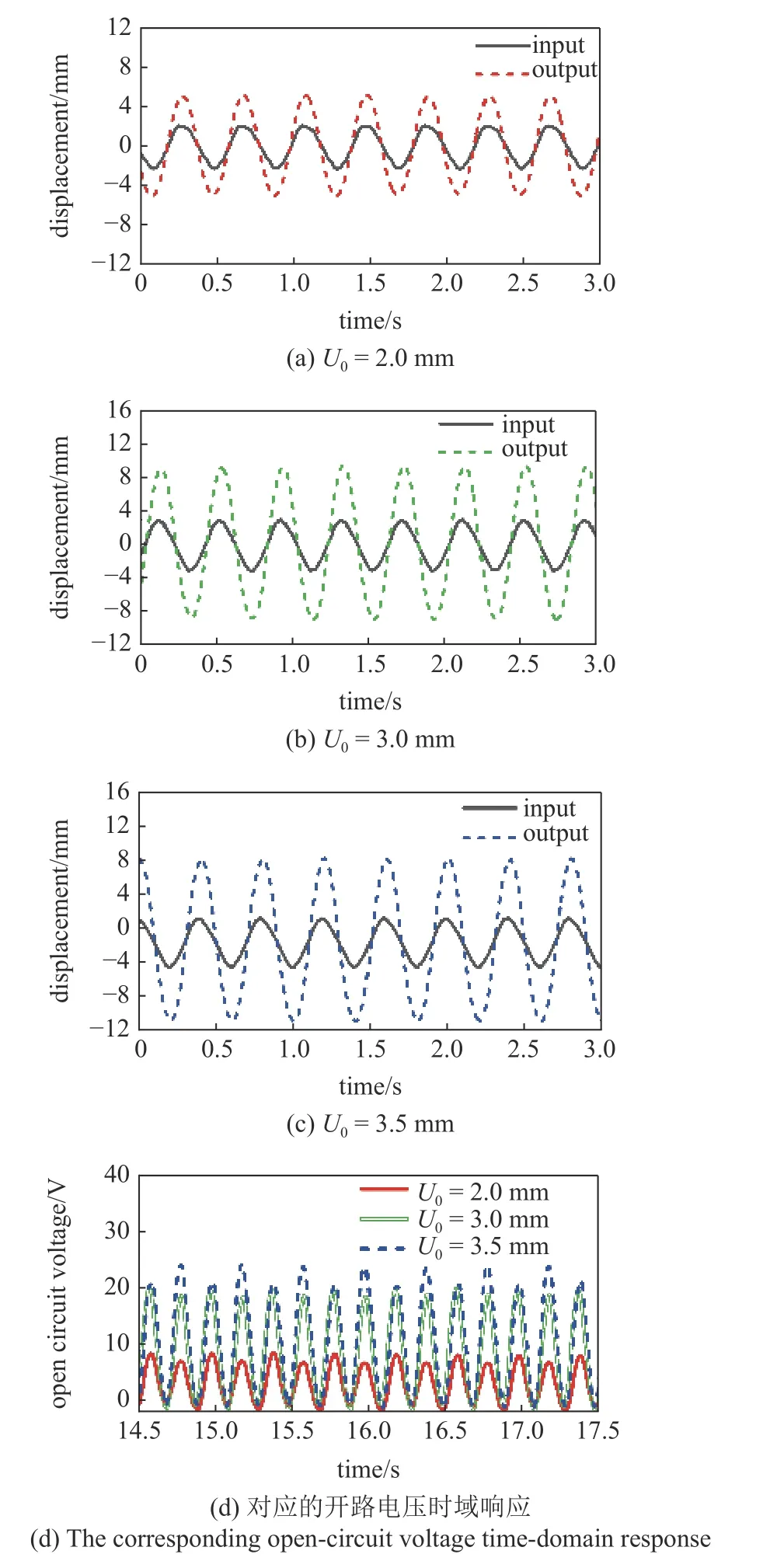
圖9 在2.5 Hz 時,不同激勵幅值的位移時域響應曲線Fig.9 The displacement time-domain response curve with different excitation amplitude at 2.5 Hz

4 結論

本文針對傳統線性共振型振動能量采集方法以及非線性多穩態振動能量俘獲方法難以實現低頻小幅值工況下振動能量的高效俘獲難題,創新設計了一種由準零剛度系統驅動能量轉化單元實現大幅值運動響應的準零剛度驅動式壓電能量采集系統.因能量轉化單元為構成準零剛度系統的一部分,所以其高效能量采集頻率與頻帶不依賴于能量轉化單元的固頻,而是與準零剛度系統的動力學響應嚴格相關,克服了傳統線性共振型能量采集難以實現低頻俘能的難題.另外,準零剛度驅動式能量采集系統在靜平衡位置處剛度等于零,在靜平衡位置附近趨近于零,能夠在低頻小幅值工況下實現較大動力學響應,進而驅動能量轉化單元實現振動能量高效采集.本文首先用能量法獲得機電耦合動力學方程,再結合諧波平衡法推導出動力學響應與電學輸出的解析解.對比數值幅頻響應曲線與解析幅頻響應曲線發現,數值解與解析解結果相互吻合.進一步分析了系統阻尼系數與外激勵幅值對準零剛度驅動式能量采集系統動力學與電學輸出的影響,并加工制備了能量采集系統樣機,搭建了實驗測試平臺進行驗證.研究結果顯示,當外激勵頻率等于2.5 Hz、激勵幅值等于3.5 mm 時,所提出的準零剛度驅動式能量采集系統能夠產生25 V 的輸出電壓.本文研究成果有望進一步夯實低頻振動能量采集理論,為低頻小幅值振動能量采集提供新思路.