參外聯合激勵下非線性Zener 系統的減振機理研究1)

邢景點 李向紅,?,2) 申永軍?,

* (石家莊鐵道大學數理系,石家莊 050043)

? (石家莊鐵道大學機械工程學院,石家莊 050043)

** (石家莊鐵道大學省部共建交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043)

引言

工程實際中的有害振動不僅會影響機械設備的性能和使用壽命,更會給系統的安全與可靠性帶來嚴重威脅[1-2].在船舶工業[3]、鐵路運輸[4]、航空航天[5]等領域,由于外界復雜動態環境等因素的干擾,振動往往具有非線性特性,導致系統產生豐富且復雜的動力學行為.

采用減振裝置來減小有害振動對機械系統的不利影響是振動控制中常用的手段,其中黏彈性材料容易構造且具有較好的耗能性能,被廣泛應用于各類隔振、減振系統中[6-7].黏彈性是指材料同時表現出黏性流體和彈性固體特性的性質,彈性材料在拉伸和釋放時會縮回其原始位置,而黏性流體在拉動時會保持其伸展形狀.黏彈性材料結合了這兩種特性,它在受到壓力后會恢復到原來的形狀,但恢復的速度足夠慢,可以抵抗下一個振動周期[8].比較典型的線性黏彈性本構模型有Maxwell 模型、Kelvin 模型和Zener 模型,其中Maxwell 模型由一個彈簧和一個阻尼串聯而成,能夠較好地表達應力弛豫特性,但不能反映蠕變行為;Kelvin 模型是一個彈簧和一個阻尼并聯而成,與Maxwell 模型相比,能很好地表達蠕變行為,但不能反映應力弛豫現象,而具有1.5 自由度的Zener 模型可以更好地表征這兩種特性[9],它由一個彈簧并聯一個Maxwell 元件組成,該系統具有黏彈性材料的優異特性、構造簡單且具有較少的系統參數,在提高系統減振效果方面有著廣泛應用.

針對該模型,Brennan 等[10]研究了Zener 系統在自由振動和受迫振動條件下的動力學行為,探究了剛度和阻尼對系統性能的影響.焦小磊等[11]提出了歸一化的三參數隔振系統設計方法,并給出了正弦激勵以及階躍激勵下三參數隔振系統的時域響應解析形式.為了進一步改善Zener 系統的減振性能,Shi 等[12]建立四參數 Zener 模型,并實驗驗證了該模型在高頻段的減隔振性能得到了改善.Wang 等[13]引入立方剛度,改善了三參數隔振器在諧振頻率和高頻區域的傳遞特征.Silva 等[14]發現將非線性立方剛度引入主彈簧或Maxwell 元件的彈簧中都將會使高頻段減振性能得到改善.康永剛等[15]提出改進的Zener 模型,更準確地描述黏彈性材料的應力松弛行為;范舒銅等[16]提出新型非線性黏彈性能量阱,發現簡諧激勵下黏彈性非線性能量阱比傳統非線性能量阱的減振效果更優.

多頻激勵下的機械系統具有廣泛的工程背景,在實際工程中,系統在多個頻率作用下會產生復雜的振動響應以及豐富的動力學行為[17-20].Yang 等[21]研究了多頻激勵下非線性時變正齒輪系統的頻率響應特性,驗證了多頻激勵的存在會導致不同諧波激勵之間的相互作用,顯著影響系統的非線性振動特性.Dnailo 等[22]研究了在參數激勵和外部激勵作用下非線性Mathieu-Duffing 系統穩態響應,驗證了二次和三次非線性以及參數放大對擴展采集器應用性能的影響.Asnafi[23]研究了Kelvin-Voigt 黏彈性板在參外聯合激勵下的混沌行為,表明阻尼、激勵振幅和頻率將影響系統混沌區域.Yan 等[24]研究了參外聯合激勵下鐵木辛柯梁橫向振動問題,發現非線性振動中的周期運動和混沌或準周期運動隨著軸向平均速度的增加而交替進行,且激勵幅值是影響系統響應的重要參數.Mehrdad 等[25]研究了參數激勵頻率與外激勵頻率為2:1 的Duffing 型非線性系統的系統響應,利用變幅法求得系統解析解,證明了系統振動響應的有界性.

不同尺度耦合動力系統通常會呈現出簇發振動的特殊振動形式,即大幅振動的激發態和微幅振動的沉寂態的組合.當系統的激勵頻率與固有頻率存在量級差異時,系統就會呈現出多尺度的特性[26].自Rinzel 等[27]提出快慢分析法以來,針對單頻慢變激勵系統的簇發振動機制已經得到廣泛研究.為了解決不同激勵頻率之間存在差異而引起的快慢動力學問題,Li 等[28]提出了包絡快慢分析法,研究了鉑族金屬上CO 氧化過程中的簇發振蕩及其誘導機理.Han 等[29]根據De Moivre 公式提出了頻率截斷快慢分析法,解決了頻率比為m:n的參外聯合激勵系統的快慢動力學問題.基于此,更多學者對這類系統展開廣泛研究.張曉芳等[30]將參外聯合激勵引入Lorenz系統,探究了系統在嚴格共振和非嚴格共振下的簇發振蕩機制.曲子芳等[31]揭示了含雙頻周期激勵的不同尺度Filippov 系統的非光滑簇發振蕩模式及分岔機制.

目前,對于機械系統減振的研究大多集中在結構仿真與參數優化,Liu 等[32]研究了不同的阻尼結構對準零剛度隔振器隔振性能的影響,發現硬化阻尼有利于隔振性能的提升.Wang 等[33]通過實驗探究了黏彈性阻尼材料性能與溫度、頻率之間的關系,驗證了其對結構振動的抑制作用.Zhang 等[34]提出組合阻尼NES,通過數值模擬與不同NES 在不同脈沖載荷幅值下的減振效果進行對比,發現組合阻尼NES 具有更好的減振性能.此外,萬洪林等[35]研究了線性動力吸振器對參數激勵下Duffing 系統振動控制機理,發現加入吸振器后系統自治系統平衡點穩定性增強是非自治系統減振的主要原因.

低頻振動具有傳播距離遠,隔離困難等特點,且存在于多個領域,例如航天器的微振動、工程建筑、交通運輸等[36].因此,目前除了研究共振情形下的振動控制問題之外,低頻隔振減振問題也受到了廣泛的關注.Wang 等[37]研究了加入軟化硬化(SH)元件的NES 的減振性能,發現該系統可以有效降低低頻振動;Zhao 等[38]提出了車輛-準零剛度浮置板軌道耦合動力學模型,應用高靜低動非線性剛度特征,進一步優化了浮置板軌道的低頻減振效果;Zhang等[39]提出了一種具有可編程準零剛度特性的定制機械超材料,通過曲線梁的特定幾何形狀實現多個準零剛度工作范圍,可用于超低頻振動隔離.

加入Maxwell 黏彈性元件通常會使動力系統增加半個自由度,因此會增加系統的復雜性,目前關于此類系統減振機理方面的研究工作較少.基于此,本文研究了參外聯合激勵下Zener 系統的減振機理,其中參數激勵為低頻激勵.采用包絡快慢分析法,將低頻激勵作為慢變參數,結合非自制系統與自治系統相關性,重點討論了系統的減振效果、分岔機制、減振機理,為參外聯合激勵下低頻振動機理究提供了新的思路.

1 系統方程與減振效果

1.1 系統方程

具有參數和強迫周期激勵的非線性Duffing 系統為

其中m1是系統的等效質量,為系統的等效阻尼,,和 ω1分別是系統參激剛度、振幅和頻率,為系統非線性剛度系數,和 ω2分別是系統外激勵幅值和頻率.系統(1)涉及多個頻率的耦合,存在大幅振動.為了減少大幅振動對系統的危害,對系統(1)耦合一個Maxwell元件,變為1.5 自由度非線性Zener 系統,如圖1 所示,其中ks是參激剛度和非線性剛度部分,和分別是Maxwell 元件的阻尼和剛度

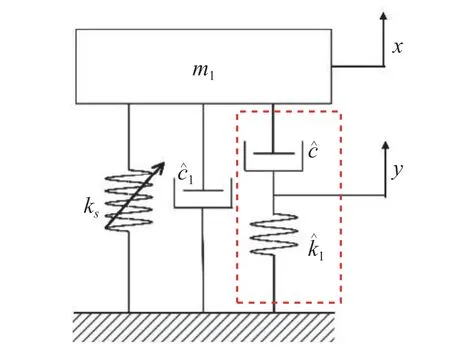
圖1 非線性Zener 模型Fig.1 Nonlinear Zener model

引入變換

系統(1)與系統(2)分別變為如下系統

分別寫為如下狀態方程

1.2 減振效果

下面研究在參數取k=0.1,b=3,c1=0,ω1=0.01,α=1,F0=0.3,ω2=0.1,c=0.4,k1=0.5時,系統(5)和系統(6)不同的動力學行為.

原系統(5)的振動行為如圖2 所示,其中圖2(a)是位移時間歷程圖,圖2(b)為相圖.可以發現軌線振幅趨于增大,這表明系統處于大幅高頻振動的發散狀態,同時系統一直呈現激發態振動.

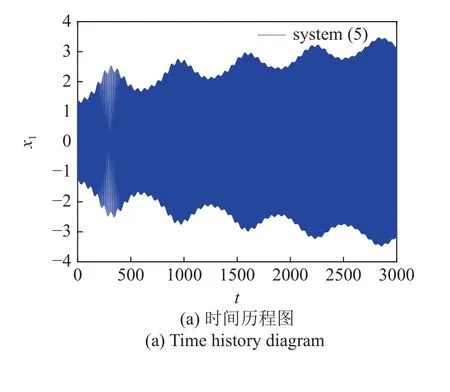
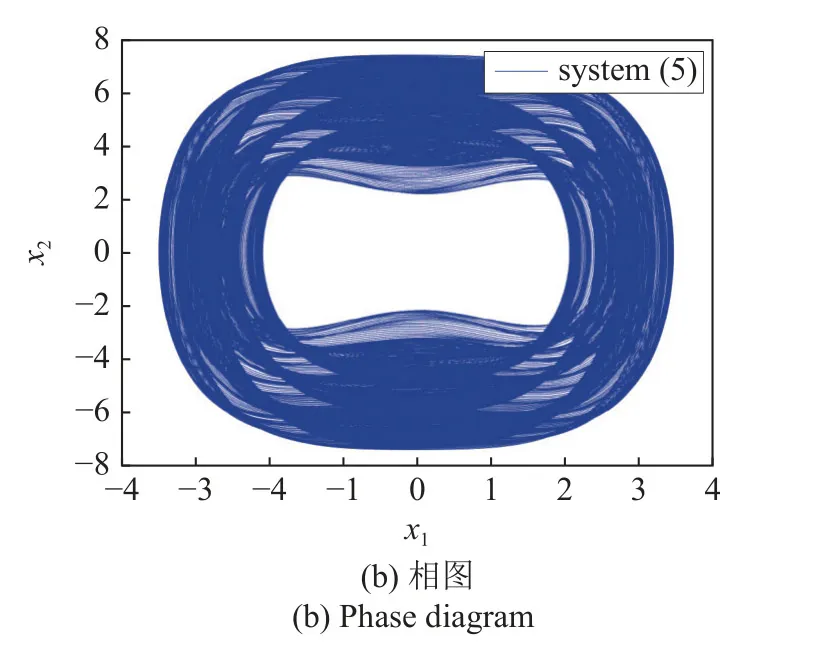
圖2 系統(5)振動響應Fig.2 Vibration response of system (5)

耦合Maxwell 元件后,取參數c=0.4,k1=0.5,系統(6)的振動行為如圖3 所示.通過對比,發現耦合Maxwell 元件后,系統高頻振動大幅降低,出現激發態與沉寂態相結合的混合振動模式,即簇發振動.從兩個相圖中明顯看出,系統位移降低了約50%,速度衰減了近90%.

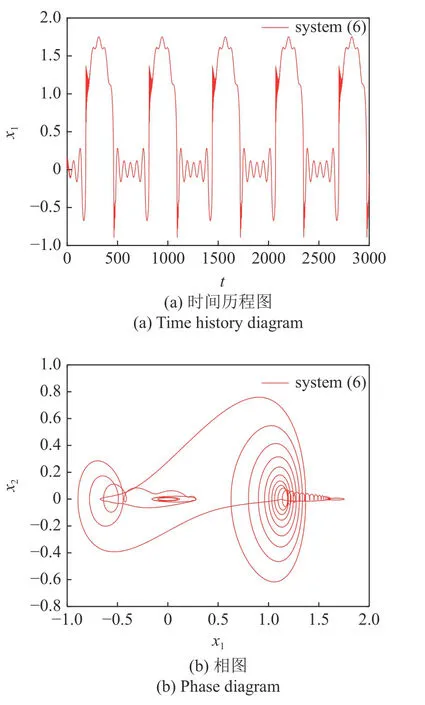
圖3 系統(6)振動響應Fig.3 Vibration response of system (6)

2 自治系統的穩定性和分岔分析

下面將深入研究加入Maxwell 元件后系統的減振機理.由于系統中各狀態變量的振動行為不但受系統的固有頻率的影響,同時又會受到參激和外激的調制,其中參數激勵為慢變激勵,因此采用快慢動力學中的包絡快慢分析法[28]揭示減振機理.令F=bcos(ω1t),當ω1<<1時,在振動周期? 內,取t在[t0,t0+?] 變化,則F在Ft0=bcos(ω1t0)和Ft0+?=bcos[ω1(t0+?)] 內變化,由于ω1很小,使得Ft0與Ft0+?非常接近,所以參數激勵F可近似看作常數,為系統的慢變過程,可視為慢子系統,x(t),y(t)為快變量,構成快子系統,則方程式(5)與式(6)都是快慢耦合的非自治系統.再令P=F0cos(ω2t),顯然外激勵P始終在P1=F0和P2=-F0之間變化.

因此考慮如下自治系統

自治系統(7)和系統(8)與非自治系統(5)和系統(6)的振動密切相關,尤其自治系統的穩定性變化和分岔行為將會對非自治系統的振動產生較大影響.具體而言,自治系統平衡點的穩定性影響著非自治系統振動的收斂和發散趨勢;而當自治系統產生分岔行為時,往往會使非自治系統的振動發生變化.此外,分岔參數的周期性變化也會導致自治系統對非自治系統的影響呈現出周期性的變化.

未加入Maxwell 元件自治系統(7)的平衡點為E(x1,0),其中x1為方程 α+(k+F)x1-P=0 的實根,由盛金公式可計算出

自治系統(7)平衡點的穩定性由以下特征方程決定

自治系統(8)的平衡點穩定性由以下特征方程決定

當a0>0,a2>0,a2a1-a0>0 時,平衡點穩定,具體的平衡點類型及穩定性可以通過數值模擬得到.

考慮參數P固定時系統運動狀態隨參數F的變化情況,當P≠0 時,在臨界點右側,系統有一個平衡點,在臨界點左側,系統有3 個平衡點,系統發生破缺分岔.

下面給出在參數取k=0.1,b=3,c1=0,ω1=0.01,α=1,F0=0.3,ω2=0.1,c=0.4,k1=0.5時,系統(7)和系統(8)分岔圖以及平衡點穩定性的變化情況,進一步揭示系統減振機理.

圖4 是系統(7)關于參數F的分岔圖,其中紅線為P=0.3 時的分岔情況,藍線為P=-0.3 時的分岔情況,整體兩組平衡線關于x1=0 對稱,且在F=-0.946 9處發生破缺分岔.平衡曲線的穩定性可由式(15)確定,其中平衡線SE1,SF1,SE2,SF2的特征值分別為一對實部為0 的共軛虛根,平衡點類型為中心;平衡線SE3,SF3特征值為一正一負兩個實根,平衡點類型為鞍點.圖中實線代表穩定的平衡曲線,虛線代表不穩定的平衡曲線.平衡點個數隨著F的減小發生變化,P=0.3 時,在分岔點IB1,IB2右側系統只有一個平衡點,在分岔點左側系統變為了3 個平衡點;P=-0.3 時在分岔點IB3,IB4右側系統只有一個平衡點,在分岔點左側系統變為了3 個平衡點.

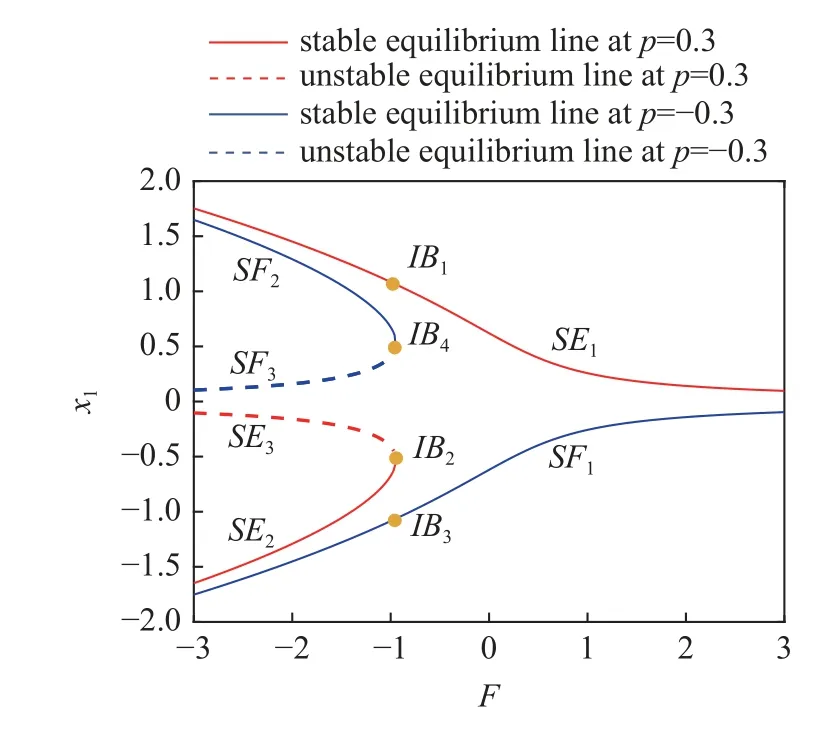
圖4 系統(7)關于 F 的分岔圖Fig.4 The bifurcation diagram of system (7)with respect to F

加入Maxwell 元件后,系統(8)平衡線的分岔圖如圖5 所示,由于平衡線方程相同,所以系統(8)平衡點分岔情況形式上與系統(7)一致.其中紅線表示P=0.3 時系統的平衡線,藍線表示P=-0.3 時系統的平衡線,實線代表穩定的平衡曲線,虛線代表不穩定的平衡曲線.平衡線的穩定性可由式(19)確定,每個平衡點有3 個特征根,平衡線SE1,SF1,SE2,SF2特征值分別為一個負實根和一對實部為負的共軛復根,平衡點類型為穩定焦點.平衡線SE3,SF3特征值為一個正實根和一對實部為負的共軛復根,平衡點類型為鞍點.相較于系統(7),雖然都發生了破缺分岔,但平衡線SE1,SE2,SF1,SF2的平衡點類型由中心變為了穩定的焦點.

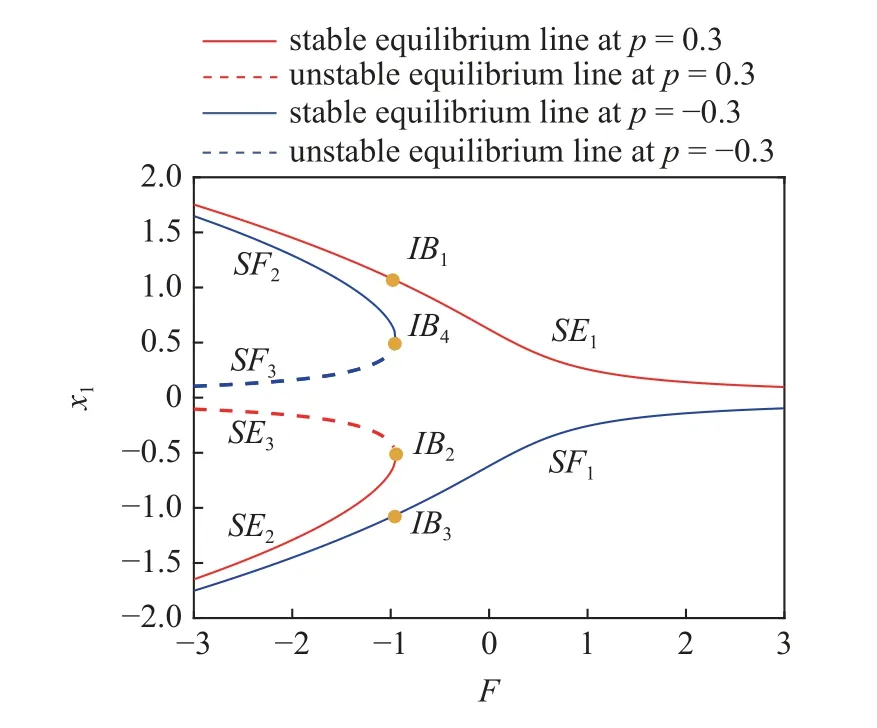
圖5 系統(8)關于 F 的分岔圖Fig.5 The bifurcation diagram of system (8)with respect to F

3 簇發振動與減振機理分析

為深入理解減振機理,并清楚展示自治系統穩定性與分岔是如何影響該非自治系統的振動行為,采用包絡快慢分析和轉換相圖進行闡述.如圖6 所示,將系統(5)在 (F,x1)平面上的轉換相圖與平衡線分岔圖進行疊加,更好地觀察在各平衡態附近的軌線性態,可以發現,未加Maxwell 元件的系統由于自治系統的平衡點類型為中心,平衡線對非自治系統軌線的吸引性很弱,因此系統(5)始終呈現大幅振蕩現象.

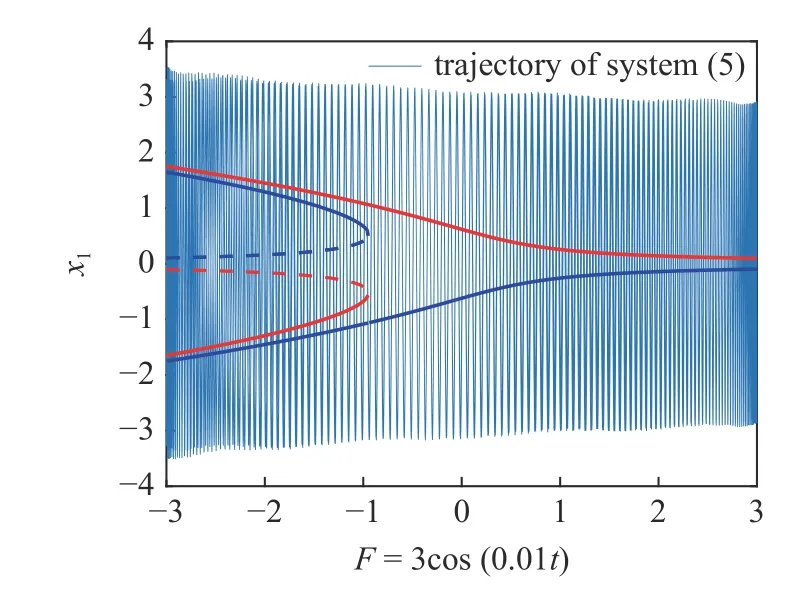
圖6 系統(5)轉換相圖與分岔圖疊加Fig.6 The overlap of transformed phase portrait and bifurcation diagram of system (5)

加入Maxwell 元件后,系統軌線在一個振動周期內,存在著明顯的簇發現象,如從圖7 中可以看出,該周期簇發振動分成4 個部分,SP1-QS1-S P2-QS2,其中SP1,S P2為激發態,QS1,QS2為沉寂態.

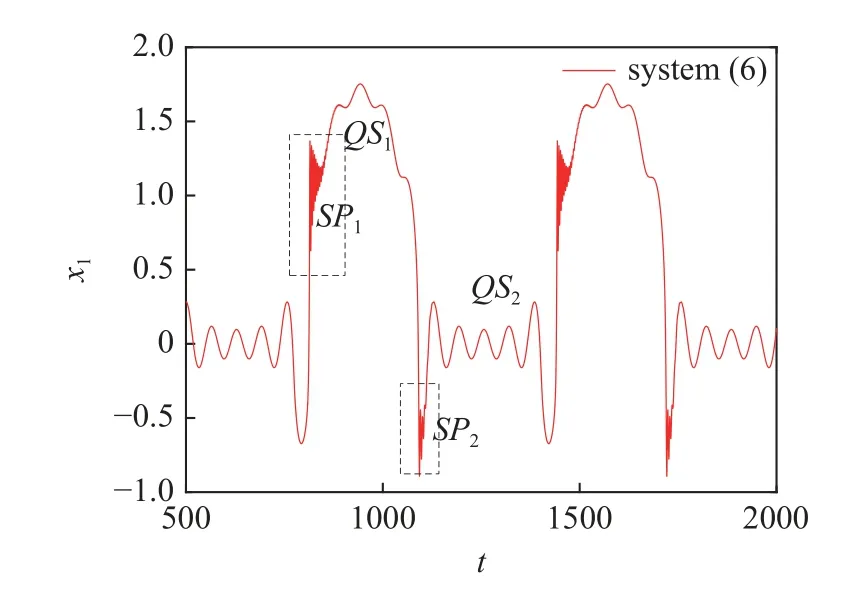
圖7 系統(6)時間歷程圖放大圖Fig.7 Enlargement of time history diagram of system (6)

下面利用包絡快慢分析法揭示振動機理.圖8(a)是系統(6)的轉換相圖,可以看到狀態變量x1隨慢變參激F=3cos(0.01t)變化而變化的過程.圖8(b)是系統(6)轉換相圖與平衡線分岔圖的疊加,隨著外激勵的值從P1到P2變化,周期性振蕩的整個軌跡幾乎都包裹在兩條平衡線SE1,SF1之間,在破缺分岔點附近,振動軌跡向上偏移,轉移到SE1,SF2兩條平衡線之間.

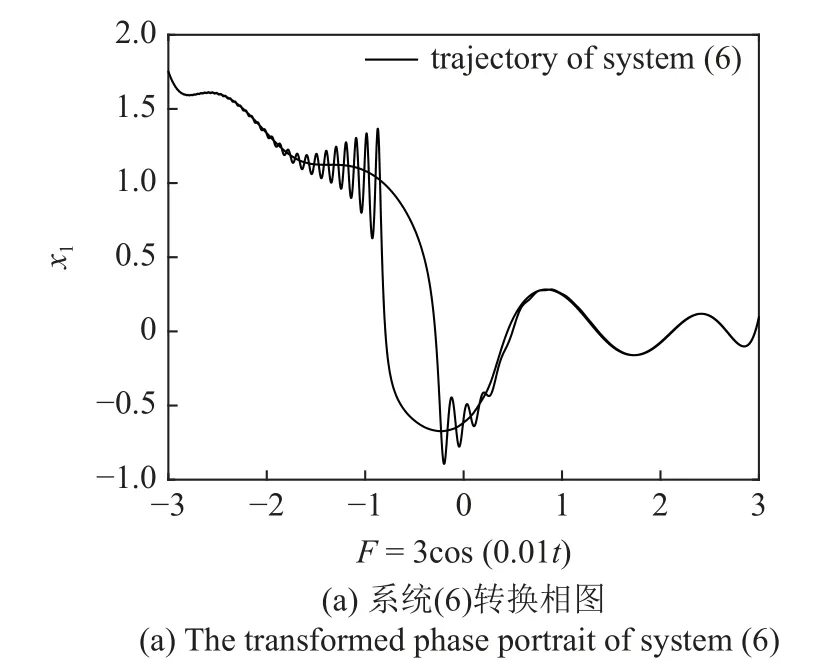
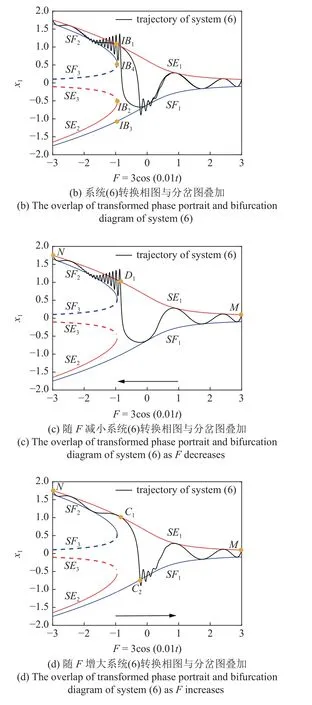
圖8 簇發現象產生機理Fig.8 Generation mechanism of bursting phenomenon

為了更清楚觀察系統軌線運動狀態,將圖8 (b)分成兩個部分,一部分是隨著F減小時的變化情況,另一部分是隨著F增加時的變化情況.如圖8(c)所示,假設軌線從點M出發,非自治系統(6)受到相應自治系統(8)兩條穩定平衡線的吸引,在SE1,SF1之間向左做振蕩運動,且軌線始終包裹在兩條穩定的平衡線內.當到達點D1后,由于自治系統發生破缺分岔,軌線在平衡線SE1與SF2之間振動,形成了高頻振蕩的激發態SP1,之后振幅逐漸衰減,直至到達點N附近形成沉寂態QS1.隨著時間t的增加,當慢變參數到達極小值F=bcos(ω1t)=-3 時,軌線將會向右折返.如圖8(d)所示,軌線從N點出發包裹在穩定平衡線SE1,SF2中向右運動,系統處于沉寂態QS1,當軌線經過破缺分岔點到達點C1后,受到穩定平衡線SF1的吸引,到達點C2,并形成振幅逐漸衰減的激發態SP2,之后很快又進入沉寂態QS2,最終到達點M,至此完成一個周期的運動.同樣地,當慢變參數到達極大值F=bcos(ω1t)=3 時,軌線則會折返向左運動,下一個周期軌線會繼續在平衡線SE1,SF1,SF2的包裹下做類似的運動.

加入Maxwell 元件后自治系統的平衡點類型發生了改變,SE1,SF1,SF2的穩定性從中心變為穩定的焦點,其吸引性明顯增強,由此系統(5)的發散運動變為系統(6)的周期運動,并且振動位移和速度都有顯著的減小,系統的大幅振蕩得到明顯的抑制.此外,破缺分岔使得自治系統多個穩定吸引子共存,從而導致非自治系統軌跡在不同穩定吸引子之間跳躍.因此,在參數激勵項為慢變過程時,自治系統的動力學行為對非自治系統的振動具有明顯的調控作用.

4 系統參數對減振的影響

破缺分岔會導致系統出現突跳現象,這種現象會導致系統從一個穩定狀態跳躍到另一個穩定狀態或者在周期運動狀態之間切換,使得系統的穩定性受到一定影響[40].根據分岔條件發現可以通過改變系統剛度或者非線性項系數的方式來控制系統破缺分岔的發生,避免出現不穩定平衡點,從而實現對系統的控制和優化.

為了更好地說明這一點,給出了改變系統剛度k和非線性項系數 α 時,系統雙參數曲面和分岔曲面的疊加,系統(5)和系統(6)的時間歷程圖以及系統(8)分岔圖和轉換相圖的疊加,進而展示在不同條件下系統的運動狀態,以更好地理解如何通過控制系統參數實現系統優化.

4.1 系統剛度k

改變系統剛度k,其他參數與第3 節取值相同,給出加入Maxwell 元件之后自治系統(8)中x1關于F和k的雙參數分岔曲面,如圖9(a)所示,其中紅色為P=0.3 時雙參數分岔曲面,藍色為P=-0.3時雙參數分岔曲面,根據分岔條件計算出k=2.16 是破缺分岔的臨界參數值,黃色PE面為破缺分岔臨界面.可以看到PE與紅色和藍色曲面發生破缺分岔的臨界位置相切,切點在k=2.16 附近,PE面將整個區域分為兩個部分,其中紅色和藍色曲面分別在后上方region-1 區域只存在一個平衡點,在前下方region-2 區域有3 個平衡點.在圖中關于k取截面,比如k=0.1 時,截面圖如圖5 所示,取k=3時,截面圖如9(b)所示,此時在一定參數范圍內系統不存在破缺分岔.

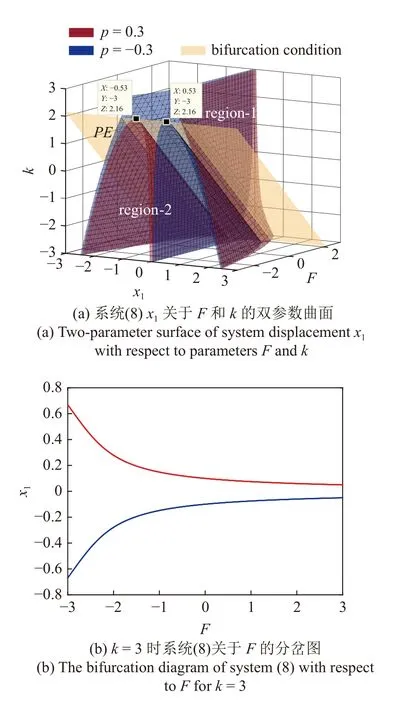
圖9 自治系統雙參數分岔曲面及在 k=3 時截面圖Fig.9 Two-parameter bifurcation surfaces of autonomous systems and cross section atk=3

k=3時,將系統(5)和系統(6)的時間歷程圖進行對比.如圖10 所示,可以看出,系統(5)呈現出明顯的大幅振蕩現象,并且呈發散趨勢.在加入Maxwell元件后,系統呈現微幅高頻和大幅低頻的混合振動模式,大幅振動得到明顯抑制,振動幅值降低到0.7 左右.系統位移降低了近80%,與第一部分k=0.1時發生破缺分岔相比,減振效果得到了明顯的提高.其減振機理由圖11 給出,可以發現k=3 時,系統(8)不再發生破缺分岔,系統(6)的軌線幾乎完全包裹在兩條平衡線之間,從而達到減振的效果.

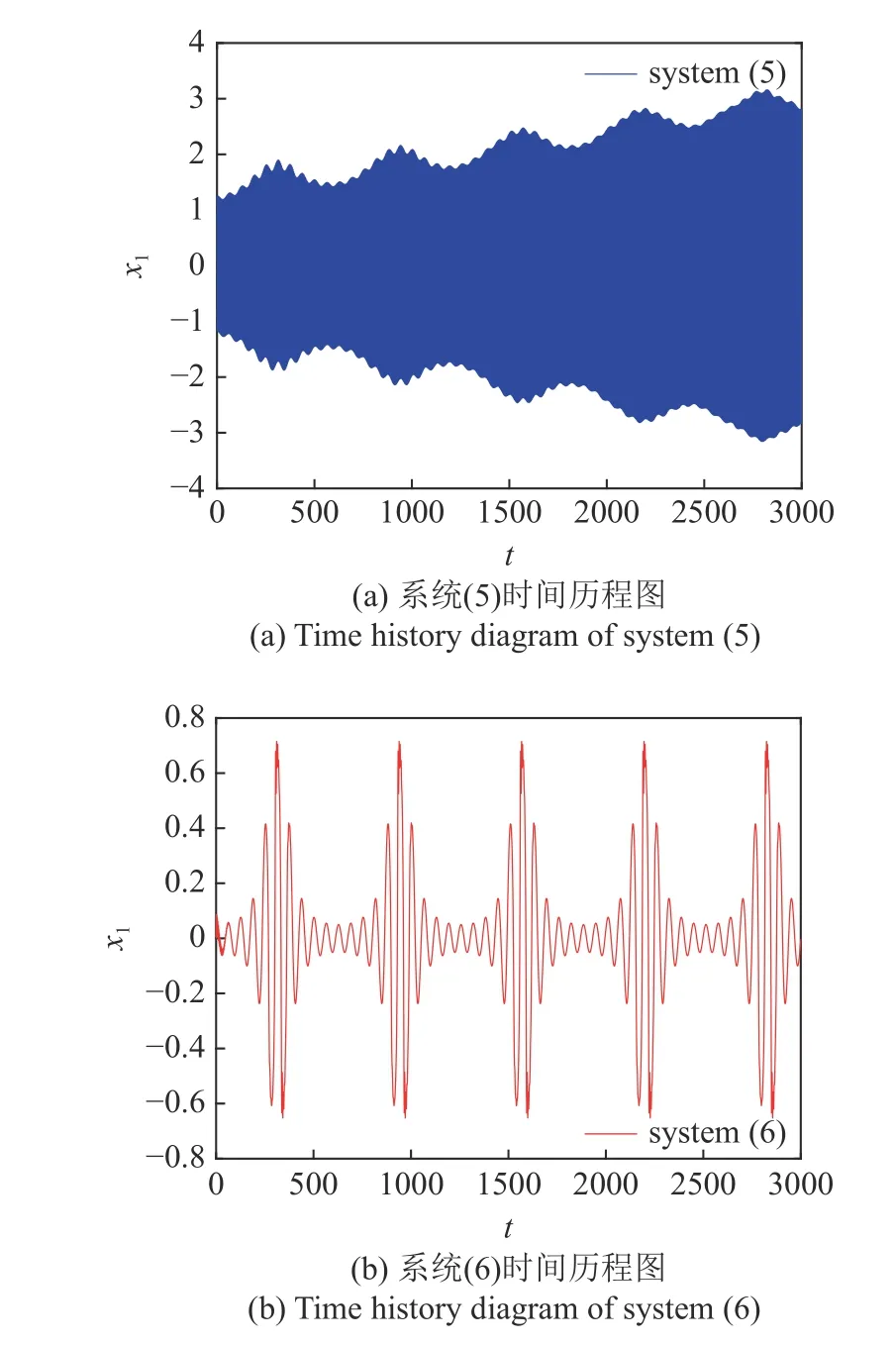
圖10 k=3 時系統(5)與系統(6)時間歷程圖Fig.10 Time history diagram of system (5)and system (6)fork=3

圖11 k=3 時系統(6)轉換相圖與平衡線疊加Fig.11 The overlap of transformed phase portrait and bifurcation diagram of system (6)fork=3

如圖12 和圖13 所示,給出加入Maxwell 元件前后k=4 和k=10 時的時間歷程圖,系統均不再發生破缺分岔,且在k=4 時系統位移幅值降低約90%,在k=10 時系統位移幅值降低近99%,即當k≥2.16時,k取值越大,系統減振效果越明顯.

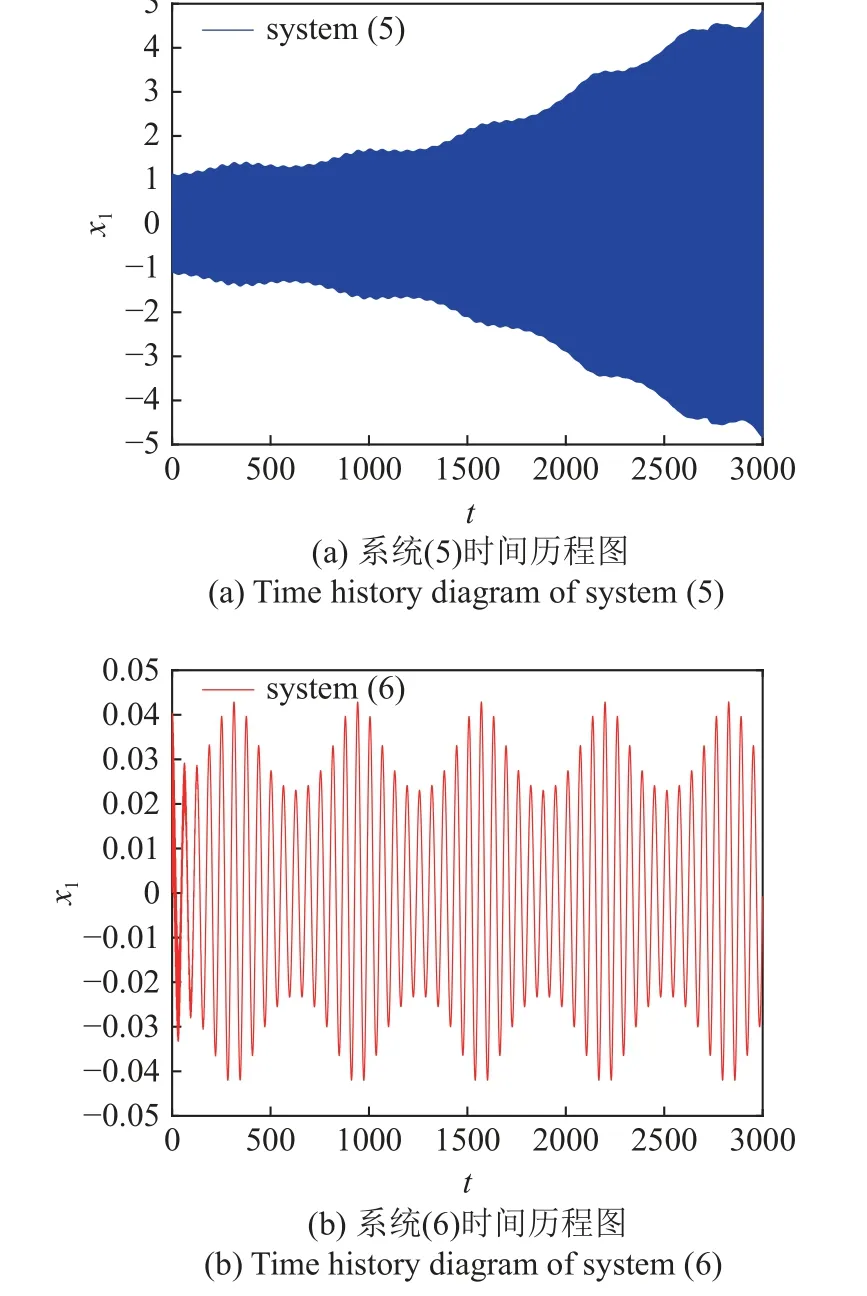
圖13 k=10 時系統(5)與系統(6)時間歷程圖Fig.13 Time history diagram of system (5)and system (6)fork=3

4.2 系統非線性項系數α

參數b,ω1,k,ω2,c,k1,F0與第3 節取值相同,改變系統非線性項系數 α,根據分岔條件計算出大約在 α ≥40.15 時,系統不發生破缺分岔.

如圖14 所示,給出自治系統(8)中x1關于F和α的雙參數曲面,其中紅色為P=0.3 時雙參數分岔曲面,藍色為P=-0.3時雙參數分岔曲面,黃色PE面為由分岔條件計算得出的分岔臨界面,可以看到PE與紅色和藍色曲面發生破缺分岔的臨界位置相切,切點在 α=40.15 附近.PE面將整個區域分為兩個部分,其中紅色和藍色曲面分別在后上方region-1 區域只存在一個平衡點,在前下方region-2 區域有3 個平衡點.圖中關于 α 取截面,比如 α=1 時,截面圖如圖5 所示,取 α=40.2 時,截面圖如圖14(b)所示.

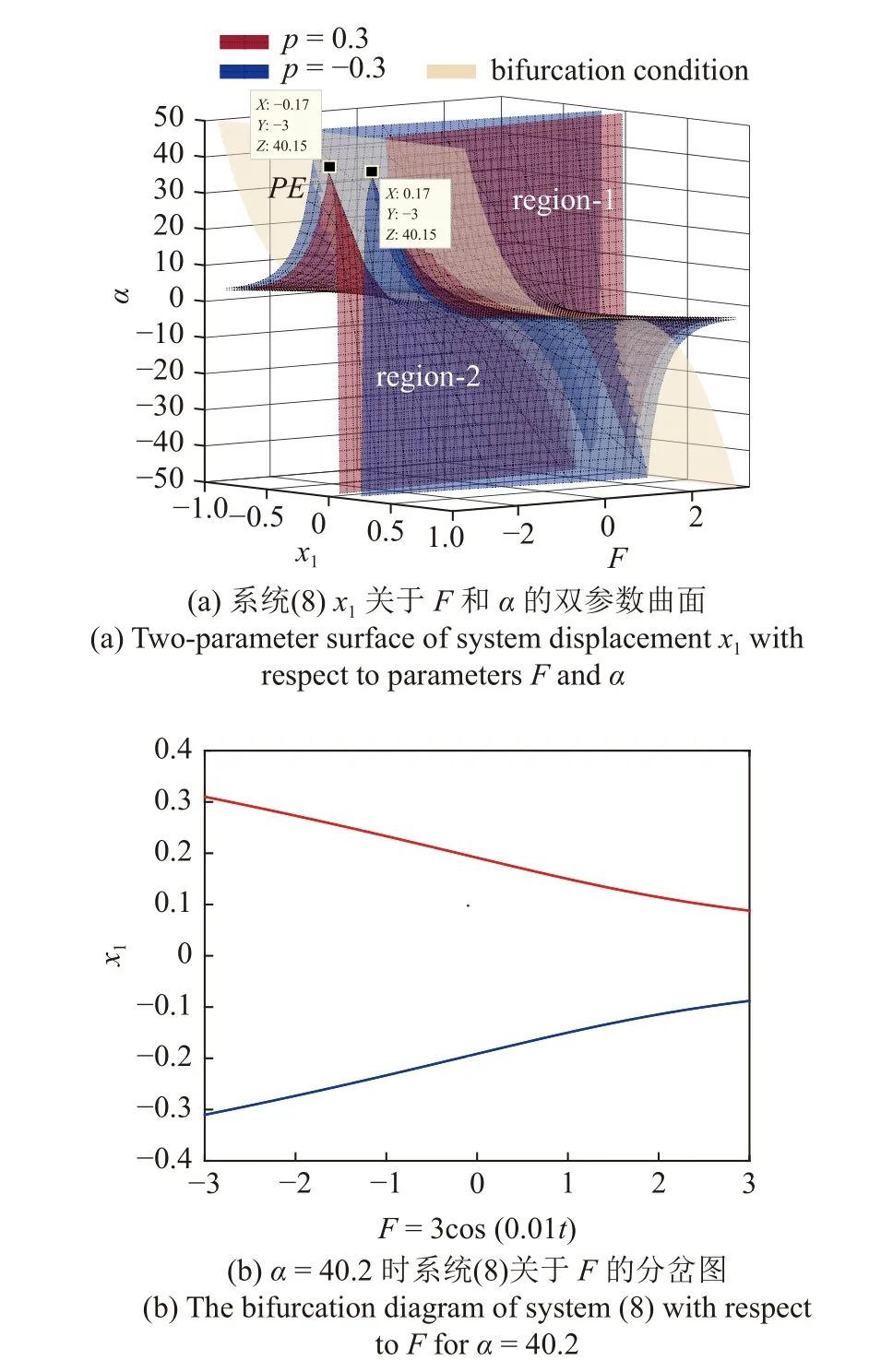
圖14 自治系統雙參數分岔曲面及在 α=40.2 時截面圖Fig.14 Two-parameter bifurcation surfaces of autonomous systems and cross section at α=40.2

給出 α=40.2 時系統(5)和系統(6)的時間歷程圖對比,如圖15 所示.可以看出,系統(5)呈現出明顯的大幅振蕩現象,在耦合Maxwell 元件后,系統呈現周期性簇發振動,大幅振蕩得到明顯抑制,振幅縮減50%以上.圖16 是系統(6)轉換相圖與平衡線疊加,可以看到系統不再發生破缺分岔,軌線幾乎完全包裹在P=±0.3 兩條平衡線之間.

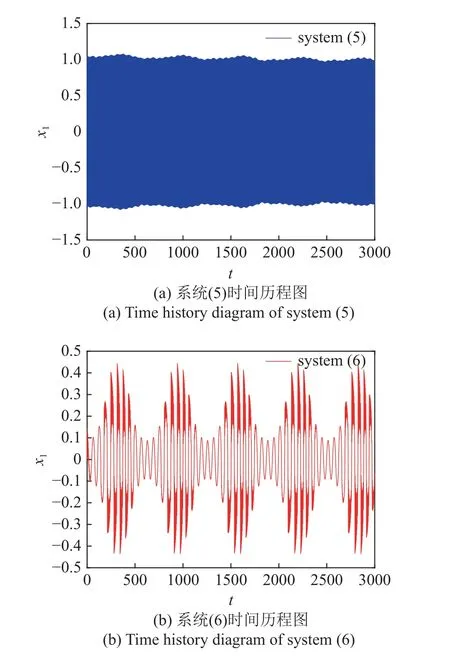
圖15 α=40.2 時系統(5)與系統(6)時間歷程圖Fig.15 Time history diagram of system (5)and system (6)for α=40.2

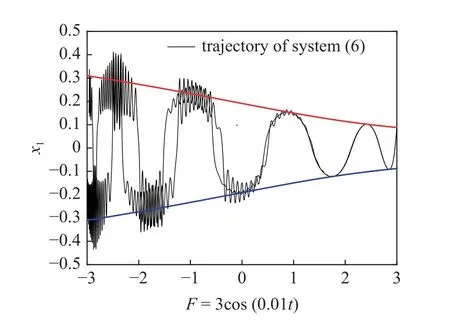
圖16 α=40.2 時系統(6)轉換相圖與平衡線疊加Fig.16 The overlap of transformed phase portrait and bifurcation diagram of system (6)for α=40.2

如圖17 所示,給出加入Maxwell 元件前后α=50時的時間歷程圖,此時系統不再發生破缺分岔,且在 α=50 時系統位移幅值降低約60%,優于α=1時的減振效果.

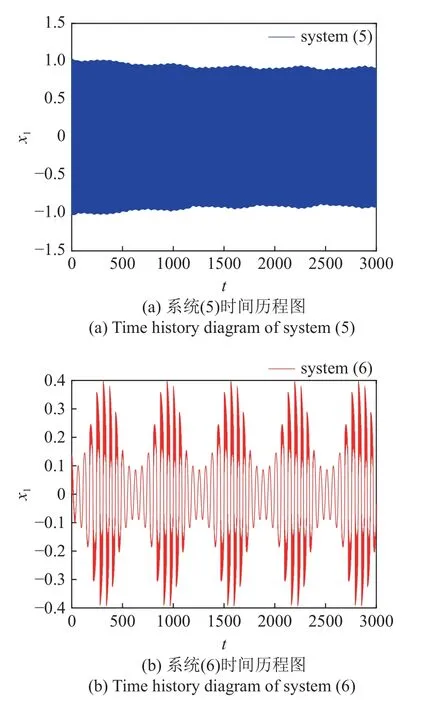
圖17 α=50 時系統(5)與系統(6)時間歷程圖Fig.17 Time history diagram of system (5)and system (6)for α=40.2

5 結論

本文以具有周期性低頻參數激勵和外激勵的Duffing 系統為例,探究耦合Maxwell 元件后,Zener 系統的振動控制問題.發現原系統的大幅高頻振動在耦合Maxwell 元件后出現了激發態和沉寂態結合的簇發振動,并且位移和速度的振動幅值都明顯降低.基于自治系統與非自治系統動力學行為的相關性,對耦合Maxwell 元件前后系統的穩定性和分岔進行了分析,發現系統發生破缺分岔.采用包絡快慢分析法,將低頻參數激勵視作慢變量,結合外激勵項被最值包絡思想,詳細給出了非自治系統受自治系統調節的機理.發現系統減振的主要原因有兩個,其一是平衡點穩定性變化使得自治系統平衡線對非自治系統軌線的吸引性增強,導致軌線振動振幅降低;其二是非自治系統軌線總是在兩條穩定的平衡線之間振動,也就是說,自治系統的平衡線限制了非自治系統的振動范圍.另外,基于雙參分岔分析,給出破缺分岔臨界面,發現系統不發生破缺分岔的減振效果明顯優于發生破缺分岔的減振效果.因此通過調節系統剛度系數和非線性項系數可以控制系統破缺分岔的發生,進而增強系統穩定性,提高系統的減振性能.