多源數據融合的雷達威力范圍評估分析方法研究

劉鎮瑜，林 歡，燕明亮，李詠晉，陳 磊

(中國人民解放軍63891部隊，河南 洛陽 471003)

0 引言

雷達對目標進行連續觀測的空域稱作探測范圍，又稱威力范圍[1-2]。威力范圍是雷達的一項重要性能指標，通過測試數據對威力范圍進行評估分析，可以有效地檢定雷達的威力范圍。由于時間、人力、空間等資源限制，雷達威力范圍的測試數據是有限的，也即小樣本數據，如何基于有限數據對雷達威力范圍進行評估分析是一項難題。傳統方法多假定威力范圍服從正態分布，然后采用樣本均值和檢驗統計量來確定威力范圍的點估計和區間估計，這種方法一般存在較大誤差。文獻[3]-[5]采用貝葉斯小子樣理論對小樣本數據進行處理，評估分析精度相比傳統方法有較大提高，但是要求驗前和驗后數據相互獨立并且服從相同的分布。

本文基于雷達方程，提出了一種基于多源數據融合的雷達威力范圍評估分析方法，該方法認為不同雷達的測試數據是存在內在關聯的，找到這種關聯關系，融合不同雷達的測試數據，可對雷達威力范圍進行更為準確的評估分析。

1 雷達威力范圍

雷達威力范圍有多種表達形式，較為直觀常見的為[6-7]：

(1)

其中，Pt為發射機功率(W)；Gt為發射機天線增益(dB)；Gr為接收機天線增益(dB)，對于單部雷達而言Gr=Gt；λ為雷達信號波長(m)；σ為目標對發射機和接收機的雷達橫截面積(m2)；k為玻爾茲曼常數，k=1.38×10-23J/K；T0為標準室溫，一般取290 K；Δfr為接收機的噪聲帶寬(也為雷達接收機帶寬)(Hz)；Fn為接收機的噪聲系數；L為雷達各部分損耗引入的損失系數；SN為雷達檢測信噪比。

式(1)中，Pt、Gt、Gr、λ、Δfr、Fn、SN為雷達工作的性能參數，數值較為固定，可通過查閱手冊獲得；k、T0為常量，不會發生變化；相對而言σ、L較為復雜，存在較大的隨機偶然性。目標的雷達橫截面積σ可通過對目標的長期觀測獲取其統計分布數據。損耗系數L可分為[8-9]雷達接收綜合損耗Lr、雷達發射綜合損耗Lt和其他損耗Lo，雷達發射綜合損耗Lt通常用2 dB的數量來近似，雷達接收綜合損耗Lr通常用1 dB來近似，其他損耗Lo包含天線波束形狀損耗、目標起伏損耗、操作損耗、大氣損耗、多徑損耗等，由于情況復雜，故不易測量獲得。

根據以上分析，將式(1)中的固定值和雷達參數相關的變量進行聚合，式(1)可表示為：

(2)

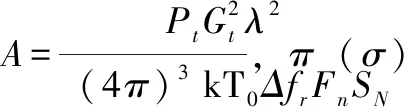
A中包含了影響雷達威力范圍的個性因素，需要從雷達本身的工作狀態參數中獲取；π(σ)和π(Lo)包含了影響雷達威力范圍的共性因素，需要從多源數據中進行分析獲取，這就為多源數據關聯融合分析提供了理論依據。

2 數據分析方法

2.1 傳統方法

威力范圍測量數據X=(x1，x2，…，xn)是服從正態總體的獨立同分布樣本。在分布的方差未知情況下，傳統統計方法給出的威力范圍點估計為：

(3)

傳統統計方法給出的威力范圍區間估計為：

(4)

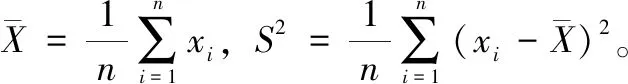
2.2 貝葉斯方法

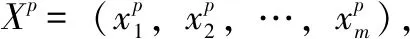
(5)

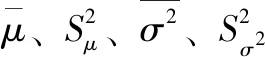
對于驗后的威力范圍數據X=(x1，x2，…，xn)，驗后分布參數為：

(6)

貝葉斯方法給出的威力范圍點估計為：

μ=μ1

(7)

貝葉斯方法給出的威力范圍區間估計為：

(8)

2.3 多源數據融合方法

多源數據指不同雷達的數據，不局限于同一體制、同一型號，甚至是同一部雷達。多源數據融合方法在式(2)的基礎上，通過多源數據確定π(σ)、π(Lo)的分布規律，再基于此分布規律來確定雷達威力范圍π(R)的分布，最后基于此分布給出威力范圍的點估計和區間估計，具體步驟如下：

(1)確定目標雷達橫截面積的分布規律π(σ)。整理目標雷達橫截面積σ數據，按照波長、目標類型等進行分類分析，根據不同類型給出σ的統計分布規律π(σ)。

(2)確定其他損耗的分布規律π(Lo)。基于式(2)，在每一組測量數據上進行多次蒙特卡羅抽樣(主要是抽樣σ)，基于抽樣值σ和雷達參數計算Lo的值。對各組數據抽樣計算完畢后，形成Lo數據集，在數據集上對Lo進行統計分析得出π(Lo)。

(3)確定雷達威力范圍的分布規律π(R)。基于π(σ)、π(Lo)的統計分析結果，對σ、Lo進行蒙特卡羅抽樣，再將σ、Lo和雷達參數代入式(2)，即可得到R數據集，在數據集上對R進行統計分析得出π(R)，基于π(R)再按傳統方法可得出R的點估計和區間估計。

3 實驗設計與分析

3.1 數據源分析

(1)目標雷達截面積數據

本文對100 000組雷達橫截面積數據(分布圖如圖1所示)進行整理，目標相對雷達姿態較為固定。

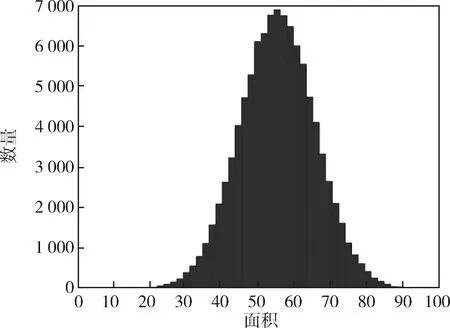
圖1 目標雷達橫截面積分布

(2)雷達數據

本文收集整理了100部雷達測試數據，每部雷達包括20組威力范圍測試數據，以及雷達的峰值功率、發射和接收天線增益、波長、接收機噪聲帶寬、接收機噪聲系數、最小檢測信噪比等參數。不同雷達的威力范圍測量數據均針對同一目標，目標飛行姿態一致。其中6部雷達的測量數據如圖2所示。

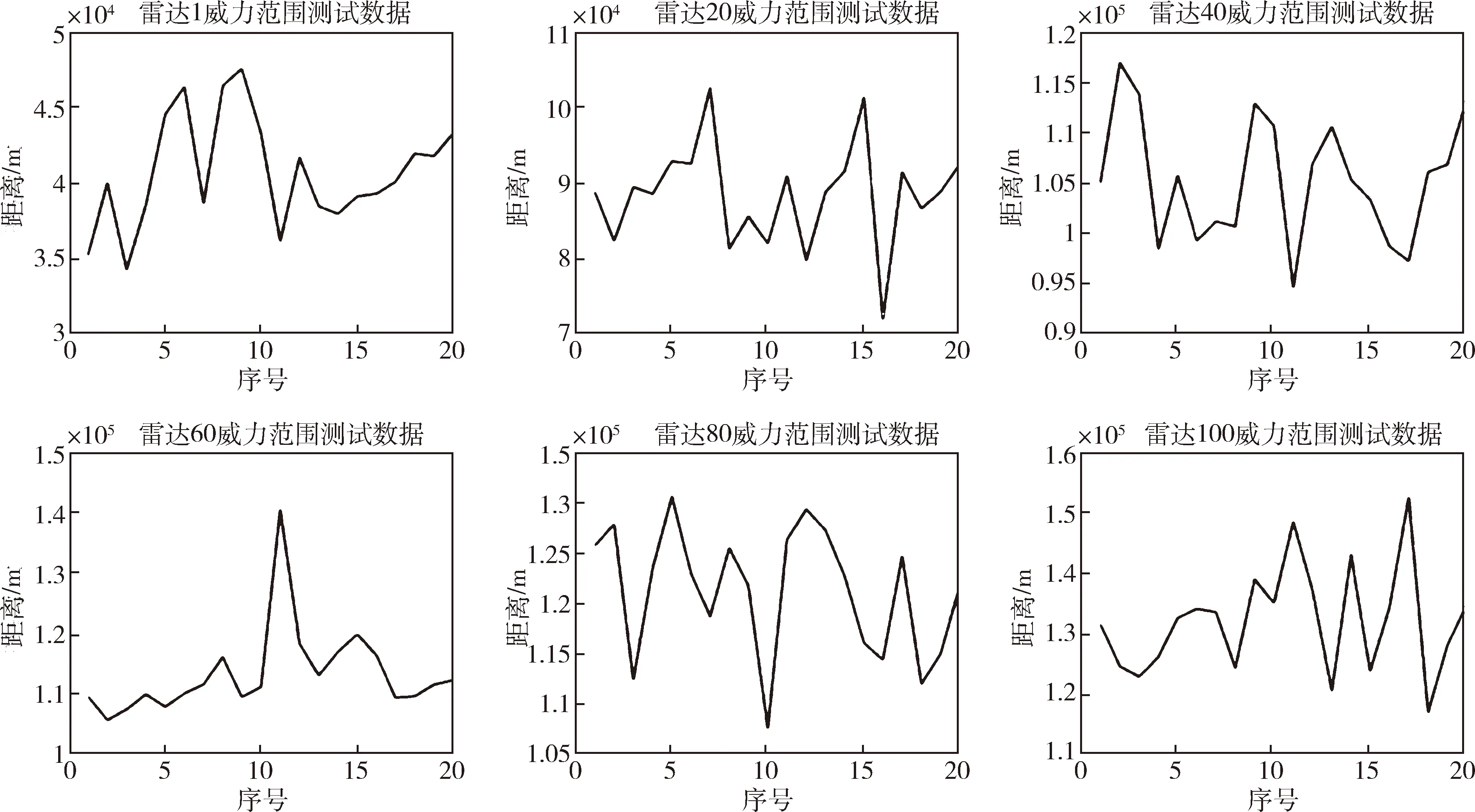
圖2 6部雷達的測量數據

3.2 數據結果分析

(1)損耗分布分析

基于多源數據融合方法，對威力范圍測試過程中的其他損耗進行抽樣統計分析，其分布結果如圖3所示。

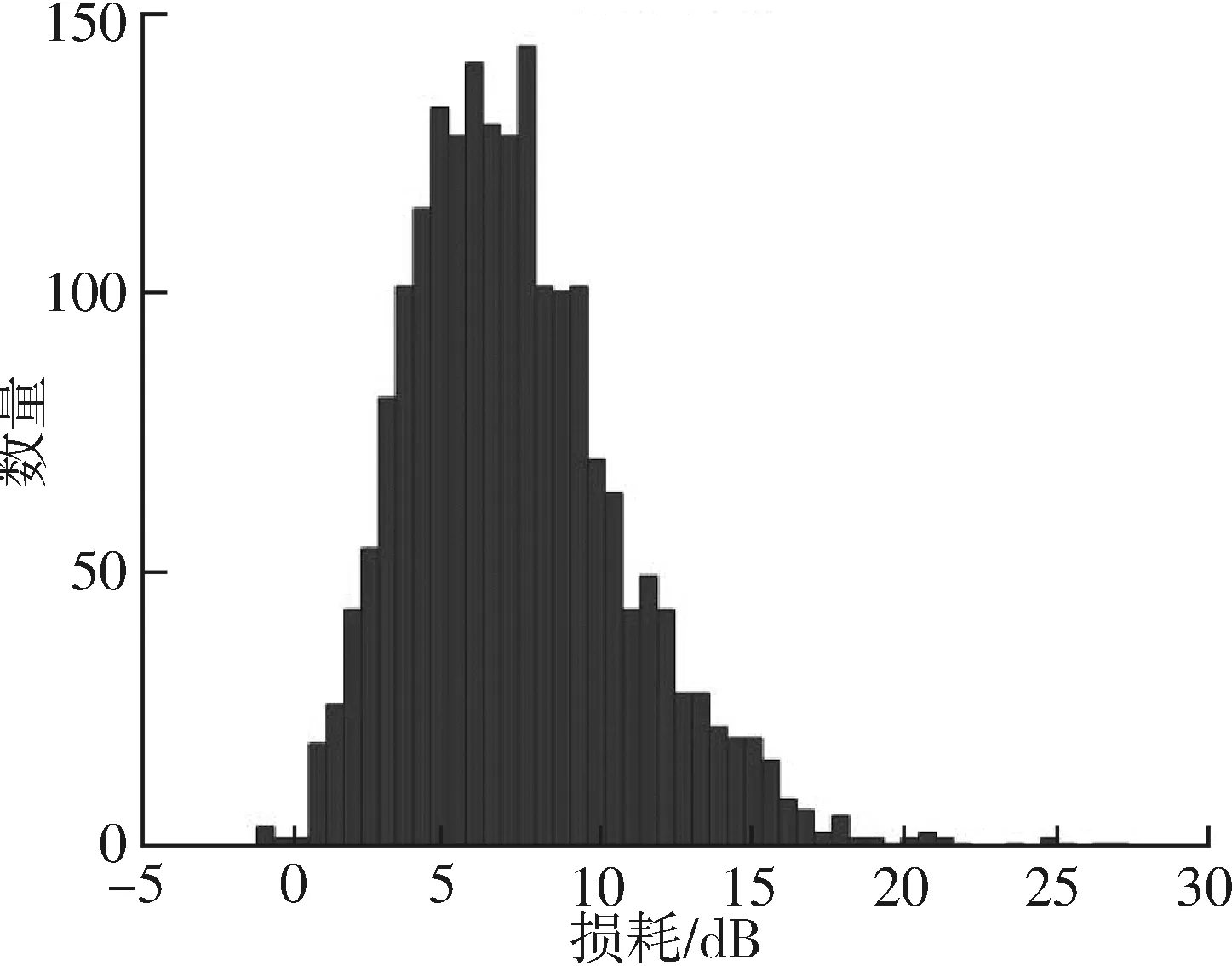
圖3 數據融合后的損耗分布

(2)威力范圍分布分析

針對100部雷達中的每一部，對目標的雷達截面積數據以及損耗分布數據進行抽樣，代入式(2)生成1 000組雷達威力范圍抽樣分布數據，其中6部雷達的威力范圍分布情況如圖4所示。

圖4 數據融合后的6部雷達威力范圍分布

(3)評估分析結果

按照第2節介紹的數據分析方法，分別按照多源數據融合方法(本文方法)、貝葉斯方法和傳統方法對100部雷達的威力范圍測試數據進行處理，威力范圍點估計(均值)如圖5所示，在置信度為90%時的威力范圍置信區間長度如圖6所示，在置信度為95%時的威力范圍置信區間長度如圖7所示，其中6部雷達的具體計算結果見表1。

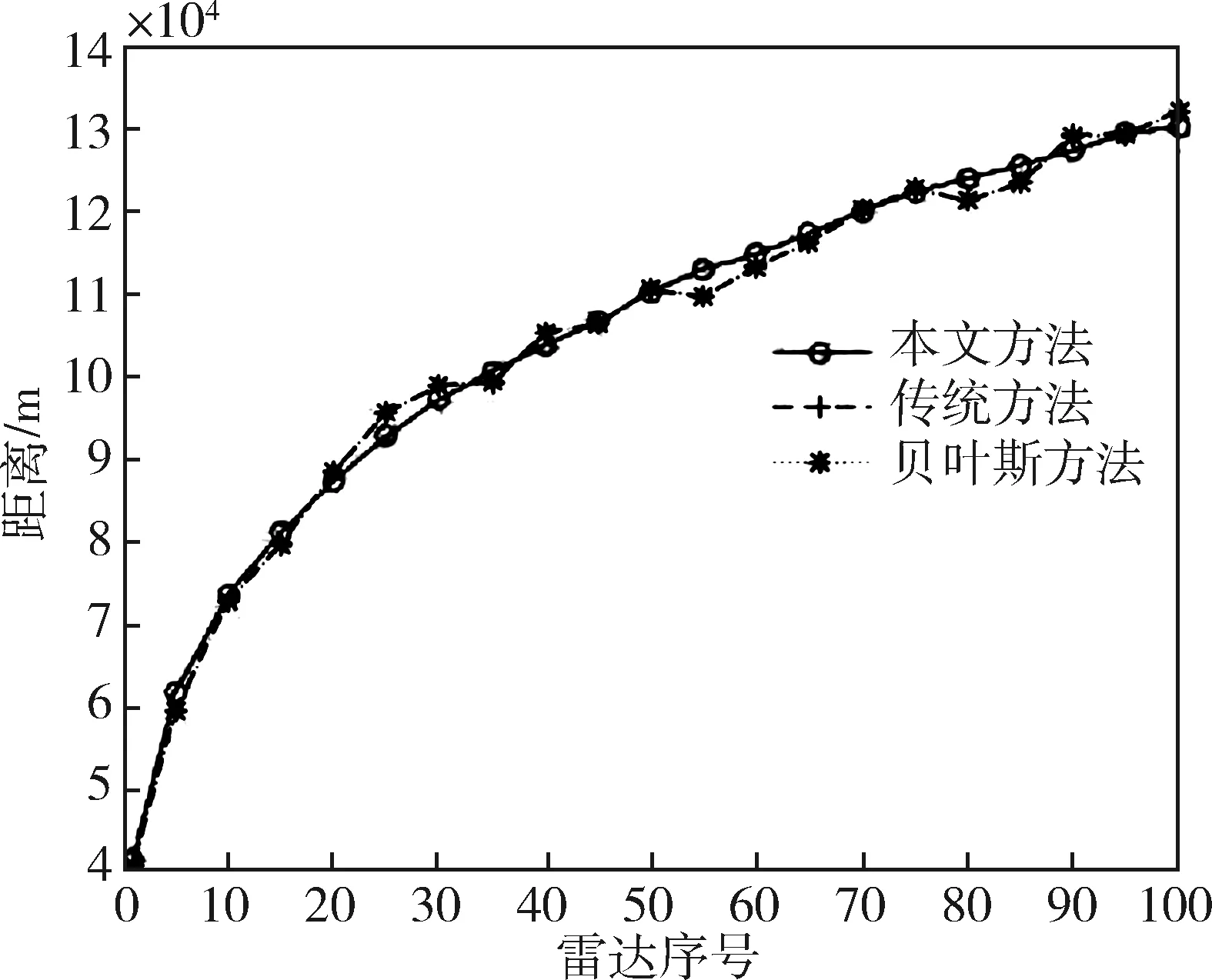
圖5 雷達威力范圍均值估計

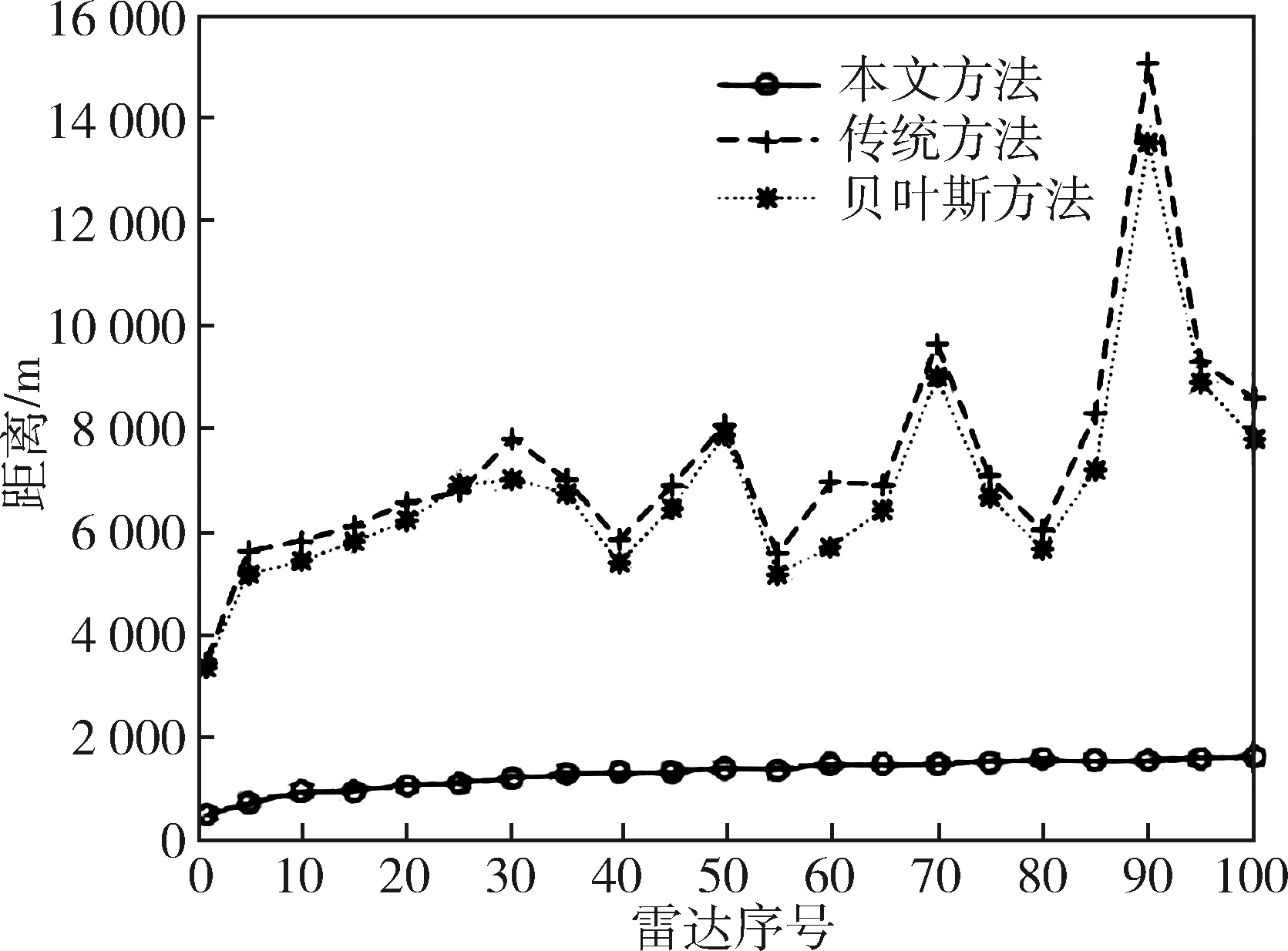
圖7 95%置信度時雷達威力范圍置信區間長度

基于以上分析結果可以看出，不同分析方法在均值結果上高度一致，反映了不同分析方法是無偏的。由于本文方法融合了多種不同來源的數據，更加客觀準確反映了數據的深層次關聯關系，從而提供了更多有用信息，因而在相同置信水平下比其他兩種方法分析得更加準確有效。

4 結論

通過分離影響雷達威力范圍的個性和共性因素，建立新的雷達威力范圍評估分析模型。在關聯融合大量不同雷達威力范圍測試數據基礎上，準確刻畫了共性因素的分布規律。基于測試數據，對比不同的數據分析方法，可以看出多源數據融合方法有明顯更短的置信區間，為雷達威力范圍評估分析提供了新的思路方法。