基于同態的多對多電子投票方案設計*
霍珊珊,李艷俊,,劉 健,羅昕銳
(1.中國電子科技集團公司第十五研究所 信息產業信息安全測評中心,北京 100083;2.北京電子科技學院,北京 100070)
0 引言
隨著網絡技術的飛速發展,互聯網所提供的各種便利服務也越來越為人們所接受與采用。與傳統的投票方案相比,電子投票方案基于密碼技術設計并通過網絡實現,投票和計票過程速度更快,投票結果也更準確,同時還能保護投票者的隱私安全,在保護公民的合法權益方面發揮著重要作用。21世紀以來,美國、瑞士等西方國家已經在國內大范圍使用電子投票系統,涉及政治、經濟等多個領域。然而,近二十幾年美國發生多起電子投票系統被黑客入侵的事件,包括將候選人票數對調、錯算選票和不計算選票等。2019年,瑞士政府賞重金邀請黑客尋找電子投票系統的漏洞。2022 年7月巴西總統認為當時使用的電子投票系統存在漏洞而要求廢除。除此之外,法國、意大利和澳大利亞等國家的電子投票系統也都曾出現過嚴重漏洞。因此,電子投票的安全性至關重要。
電子投票方案除了應該滿足傳統投票的主要功能外,還應保證投票統計速度快、投票結果真實有效等需求,大致可總結為以下幾點:
(1)合法性:只有合法投票人才能投票,合法的選票必須保證全部計入總票數。
(2)不可偽造性:非法用戶不能截獲、篡改或者偽造選票。
(3)匿名性:合法投票人的選票內容應該保密,由選票判斷不出投票人任何信息。
(4)公平性:每個投票人只能投放一張選票,多張選票無法通過合格性檢驗。
(5)不可篡改性:在保證安全性的前提下,用戶可以驗證其選票是否被篡改。
電子投票系統通常基于盲簽名、安全多方技術、秘密共享、同態加密等密碼技術設計。1992年,Fujioka等人[1]基于盲簽名提出了可適用于大規模投票的 FOO 方案,電子投票開始走向實用。1997年,Cramer等人[2]首次提出多位候選人的電子投票問題,并利用ElGamal加密系統同態性設計了多選一的電子投票方案,需要可信的計票中心接收選票并進行計票。2001年,基于Paillier加密系統的同態性Damgard等人[3]提出了一個多選多的電子投票方案,然而該方案無法避免重復投票現象。2006年,仲紅等人[4]提出一個無需第三方計票機構參與的多選多電子投票方案,該方案基于安全多方求和技術設計,但投票結束后會公開所有候選人的票數。之后,研究人員基于安全多方計算中不經意傳輸協議、求和技術分別進行了電子投票設計,然而存在實現效率不高或者應用場景受限等問題[5-7]。同時期,基于秘密共享的電子投票方案也成為研究熱點之一[8-14]。2015年,李蓓[15]采用多種密碼體制進行了電子投票方案設計,由于密碼體制較多使得交互過程步驟增加明顯。2017年,黃仕杰等人[16]基于Paillier公鑰密碼體制的同態性提出了多對一電子投票的方案,實現了不解密選票的情況下能進行計票,然而計算量大,不能適用于大規模的投票。2019年,劉霆等人[17]將隨機性分組碼的秘密分享技術應用于多候選人電子投票方案中,秘密交換次數多以致通信代價高。同年,付偉偉等人[18]基于隨機矩陣提出一個可驗證的多選一電子投票方案,需要計票中心參與,中心計算量大。2021年,邵清等[19]基于ElGamal強盲簽名和區塊鏈技術提出一種電子投票方案,由智能合約代替可信第三方進行選票合規性判斷、計票等工作,但投票人數增多時容易形成計算瓶頸。同年Lu等人[20]結合比特幣技術提出了安全電子投票系統,計算資源消耗仍然不可避免。近兩年,橢圓曲線密碼技術在越來越多的投票方案中使用[21-22],2022年高小龍等人[23]推廣了橢圓曲線密碼體制在大規模場景中的電子投票方案,降低了通信代價,但是增加了計算量。隨著量子時代的來臨,基于后量子技術的投票方案也開始出現[24-25],不過大都處于理論研究階段。
在實際現有的電子投票方案中,同態技術允許計票人在不解密的情況下對密文進行操作,更好地保證了選票的隱私性,而Paillier密碼和ElGamal密碼是最常用的選擇。Paillier密碼方便于最終計票,比ElGamal密碼的適應性更強。只是基于這種密碼體制一般容易設計多對一電子投票方案,設計多對多的電子投票方案并不容易。本文基于Paillier密碼的同態性進行設計,可信中心采用預計算三元組的方式對選票合規性進行快速判斷,計票員從總投票中計算出每個候選人的總票數,投票人、計票員的計算量小,方案實現效率高,適用于大型電子投票的場合。
1 Paillier同態密碼
同態加密方案被分成3種類型:部分同態加密、淺同態加密和全同態加密。同態加密方案在分布式計算環境下的密文數據計算方面有著重要的應用,包括安全云計算與委托計算、遠程文件存儲、密文檢索等。目前全同態加密方案的構造還處于理論階段,部分同態技術應用較為廣泛。Paillier密碼是一種成熟的部分同態技術,即具有加法同態性質,不具有乘法同態性質,下面對該密碼體制進行描述。
1.1 初始化
Paillier密碼是一種公鑰密碼算法,其密鑰生成的參數選取以及主要步驟如下:
(1)選取兩個大素數p和q;
(2)計算n=pq,λ=lcm(p-1,q-1),這里lcm表示最小公倍數(least common multiple);
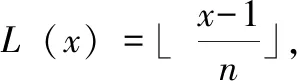
(4)隨機選取一個小于n2的正整數g,并且存在u=(L(gλmodn2))-1modn,如果不存在這樣的u,則要重新選擇g,或者從步驟(1)重新開始。
由以上步驟計算得到的公鑰為(n,g),私鑰為(λ,u)。
1.2 Paillier密碼
Paillier加密過程描述如下:
假設明文為m,0 (2)計算密文: En(g,n,m)=c=gmrnmodn2 (1) 解密過程如下: 使用私鑰計算De(g,n,c)=m,即明文: m=L(cλmodn2)·umodn (2) Paillier密碼具有加法同態性質,不具有乘法同態性質,具體分析如下: 對于兩個不同明文m1,m2,加密后得到兩個不同的密文: (3) 這兩個密文滿足以下式子,所以Paillier密碼具有加法同態性。 =En(g,n,m1+m2) (4) 假設有N位投票人和m位候選人取得了合法身份標識P1,P2,…,PN和C1,C2,…,Cm,有資格進入投票系統參與投票和計票。投票人將從m位候選人中選出t位獲勝者,每個投票人可投贊成票不超過t個,也可以棄權。 投票系統主要角色: (1)投票人:有資格參與投票的人,表示為P1,P2,…,PN; (2)候選人:有資格被投票的人,表示為C1,C2,…,Cm; (3)可信中心:檢驗投票人的身份信息,收集并公布合格投票的密文; (4)計票中心:產生最終的投票密文,并將其解密,公布勝出的候選人。 投票人Pi(i=1,2,…,N)對候選人(C1,C2,…,Cm)進行投票得到一個m元數組,每個分量tj(j=1,2,…,m)是選票計算得到的值;然后將這個m元數組交給可信中心,可信中心通過驗證公布合格票;最后計票中心計算總票數并公布排名前t的t個候選人。 本文設計的投票方案框架如圖1所示,具體分為三個階段:初始化階段、投票階段、計票階段。主要角色中的投票人、可信中心和計票員分別在不同階段行使自己的計算、核對、申訴等權利。公布欄公布相應公開信息,不能泄露任何一個角色的秘密信息。 圖1 電子投票方案框架圖 投票階段按以下步驟進行: (1)每個投票人進行注冊。投票人與可信中心互相發送數字證書,雙方進行身份認證,并協商出共享密鑰Ki,可信中心預存標識h(IDi,Ki)。 投票人將[ti,1,ti,2,…,ti,m]、h(IDi,Ki)、時間戳T以及h([ti,1,ti,2,…,ti,m]‖IDi,Ki‖T)傳輸發送給可信中心。 若計算結果為1,則候選人Cj對應的計數器增加1;若為s,則對應計數器值不變;若為s2,則對應計數器減去1。若三個值都不滿足,則該票無效,直接拋棄。 (4)可信中心將通過檢驗的合格投票在公開欄中公布,投票人通過計算h(IDi,Ki)確認自己的投票是否合格,未通過的投票可以由投票人提起申訴。 計票階段的步驟如下: (2)計票中心解密得到每個候選人Cj的票數并進行排序,然后根據要求公布排名前t位的候選人。 若有相同票數產生,則對后面幾位相同票數的候選人進行下一輪投票,直至選出t位候選人。 (1)投票階段的正確性 投票人Pi的選票Ti=[ti,1,ti,2,…,ti,m]合格時必然會對應到1,s,s2這3個值,因為: (5) 當ci=1時,式子為: (6) 當ci=0時,式子為: (7) 當ci=-1時,式子為: (8) 當ci為其他值時,投票無效。 (2)計票階段的正確性 (9) (1)合法性 只有合法投票人才有權參加投票活動,在身份認證階段會對所有的投票人進行身份驗證,這一步可以確定投票權利的投票人;具有正確標識的投票才能被接收,保證合法的投票必然是由合法投票人提交的。 (2)不可偽造性 投票人傳輸給可信中心的信息包括[ti,1,ti,2,…,ti,m]、h(IDi,Ki)、時間戳T以及h([ti,1,ti,2,…,ti,m]‖IDi,Ki‖T),其他人偽造相關信息的難度相當于破解hash函數。這樣保證了投票信息的不可偽造性。 (3)匿名性 在構造選票的過程中,使用的是Paillier公鑰密碼體制對選票進行加密,除了投票人本人,其他任何人都無法根據選票追蹤調查到相應的投票人身份,無法將選票和投票人一一對應。 (4)公平性 任何人及任何事情都不應該影響到投票的最終結果,每位合法的投票人都可以獲得自己的唯一標識h(IDi,Ki),并從公布欄查詢是否通過,如果發現中心未公布合法投票,則可以申訴。合法投票人有且只有一次投票機會,可信中心通過保留唯一標識h(IDi,Ki)確認投票次數,避免不誠信的投票人多次投票。 (5)不可篡改性 投票人可以通過公布欄確認自己的投票信息是否被篡改,同樣也可以根據公布欄中合格的投票驗證總投票是否被篡改,由此保證合格的投票不被篡改。 本文在通信需求和計算復雜度兩方面與已存在的方案(文獻[4]、文獻[15]、文獻[16])進行了分析。 (1)通信需求 由于每種方案都有投票人注冊階段,因此通信代價比較中不考慮該部分。本方案中N個投票人在投票階段進行了N次傳輸,方案的通信復雜度為O(N)。消息包含[ti,1,ti,2,…,ti,m]、h(IDi,Ki)、時間戳T以及h([ti,1,ti,2,…,ti,m]‖IDi,Ki‖T),時間戳T和hash值的長度各為256 bit,[ti,1,ti,2,…,ti,m]的長度為O(2m(log2n)),所以通信的位復雜度為O(2Nm(log2n)),優于文獻[4]的通信代價O(N2m(log2n))。文獻[15]未給出通信代價,但是采用了AES、RSA和ElGamal三種主要密碼技術,投票階段通信代價為ElGamal算法的素數域q的長度,計票階段通信代價為RSA模n的長度,高于本方案的通信帶寬需求。 (2)計算復雜度 由于初始化階段的計算不影響投票速度,因此只考慮投票階段投票人、可信中心以及計票員的計算代價。每個投票人計算m次Paillier加密,等于m次模冪(n次冪)運算,復雜度約為O(m(log2n)2),hash函數計算速度快可以忽略,N個投票人總計O(2Nm(log2n)2)。可信中心對每張選票平均計算m次模冪(λ次冪)運算,并進行m次比對,總計計算復雜度: O(2Nm(log2λ)(log2n))≈O(2Nm(log2n)2) (10) 計票中心進行(N-1)次模乘運算,復雜度總計約為: O(2(N-1)m(log2n)2) (11) 這個結果遠遠小于文獻[16]中的計算復雜度。 綜上討論,本文投票方案與類似方案的通信需求和計算復雜度比較見表1。本方案模擬實現選取的實驗環境為:系統硬件為MateBook14 AMD Ryzen 5 4600H with Radeon Graphics 3 GHz、16 GB RAM,操作系統為X64,用C語言實現。當n=2 048 bit時,模冪運算為3 703次/s。假設候選人為10個,投票人數分別選取1千、5千、1萬、5萬、10萬人時,不同的運行用時模擬如圖2所示。容易看出,在10萬人參與投票的情形下模擬時間不超過30 s,實際情形下完全可以接受。當投票人數繼續增長超過10萬人后,可信中心的計算時間會呈近似線性增長,例如達到100萬人時,需要約300 s,這時增加多個服務器實現并行計算可以節省計算時間。 表1 類似電子投票方案比較 圖2 本方案運行時間模擬 本文提出一種基于Paillier密碼設計的同態多選多電子投票方案,可以從m個候選人中選出t個勝出者,投票人、可信中心以及計票員的計算量小,方案實現效率高,適用于大型電子投票的場合。與已有方案相比,本文方案有更高的實際應用價值。然而,隨著量子計算機的成熟,Paillier密碼基于的因子分解難題容易被量子Shor算法破解,所以研究后量子時代電子投票方案將是下一步工作的重點。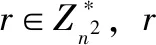
1.3 Paillier密碼的同態性
2 電子投票方案要求
2.1 投票場景
2.2 投票方式
3 基于同態的電子投票方案設計
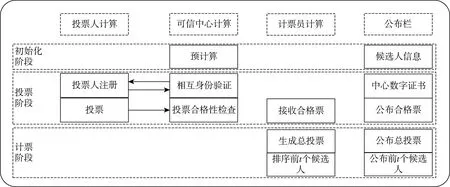
3.1 初始化階段
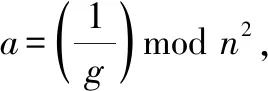
3.2 投票階段
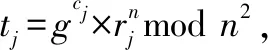
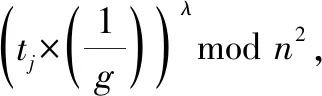
3.3 計票階段

4 系統性能分析
4.1 正確性分析

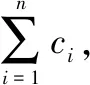
4.2 安全性分析
4.3 實驗模擬及效率分析


5 結論

