面向低能耗的密集倉儲貨位分配優化

張牧仁，項 前，呂志軍，尹英豪，俞卓韜

(東華大學 機械工程學院, 上海 201620)

四向車式密集倉儲系統(簡稱“四向車倉儲系統”)是一種新興的自動化倉儲系統,其以設備輕量靈活、空間利用率高等優點,得到了廣泛應用[1]。在“節能減排、綠色發展”理念的倡導下,物流倉儲系統的節能降耗問題已經引起了工業界和研究學者的共同關注。作為自動化倉儲的重要環節,四向車倉儲系統的貨位分配,不僅受到庫型布局、動態庫存及作業環境等約束,還與路徑優化、倉儲作業調度等問題[2-5]復雜耦合,其合理性更會嚴重影響倉儲作業能耗。

國內外關于倉儲系統能耗模型的研究主要集中在兩個方面。一方面,將能耗作為倉儲系統的評價指標指導倉庫布局優化配置。Ekren[6]以作業的能耗作為評估標準之一,提出了針對穿梭車的能耗模型;Liu等[7]進一步研究得出,在相同作業條件下,影響穿梭車倉儲系統能耗大小的因素主要是提升機的速度和加速度;Leher等[8]提出了一種用于自動化立體倉庫優化設計的能效模型。另一方面,將能耗作為優化目標應用于作業路徑、任務分配、貨位分配等問題中。Ene等[9]提出的一種能耗模型用來優化自動化立體倉庫中的復合指令作業揀選;魯建廈等[10]針對子母穿梭車密集倉儲系統,在作業路徑規劃過程中考慮設備的能耗,并將能耗作為成本添加到路徑優化模型中;方磊等[11]在動態儲位分配策略下,以堆垛機總能耗最低為目標對堆垛機的復合作業進行任務調度;Li等[12]在KMFS(Kiva mobile fulfilment system)的貨位分配問題中考慮設備能耗,并指出能耗的大小與作業距離有關,但該模型忽略了能耗對設備所載貨物質量的敏感性;柏樂[13]提出以搬運設備的能耗最低為目標的自動化立體倉庫貨位優化模型,但沒有考慮設備的作業能耗與運動特性的關系。如果能耗模型充分考慮倉儲設備的作業距離、運動特性和載貨質量等因素,其將更具有應用價值。

貨位分配作為一種組合優化問題,目前研究的求解算法多為啟發式算法,通常將多種算法混合使用或調整算法的重要步驟以改善算法性能。黃鵬等[14]針對大型重載的立體倉庫,提出將遺傳算法和延遲接受爬山算法相結合,加快了算法收斂速度;董海等[15]提出一種情緒化細菌覓食算法,求解自動化立體倉庫的最優貨位,該算法具有較好的收斂性;蔡安江等[16]改進了混合蛙跳算法,通過加入動態自適應同步因子解決了其容易陷入局部最優的問題,貨位的分配結果也更合理。差分進化算法是一種較新的啟發式算法,與遺傳算法相比,在計算速度和穩健性等方面具有一定的性能優勢[17],可用于解決實際倉儲貨位分配優化問題[18]。

綜上所述可知,現有文獻對倉儲能耗模型的研究主要側重于設備路徑優化、倉儲布局優化等,而關聯倉儲貨位分配優化的研究較少。因此,面向綠色、節能、高效的四向車倉儲系統,本文提出以節能降耗為主要目標的貨位分配優化模型及算法。

1 問題描述

四向車倉儲系統是一種新型密集自動化立體倉庫。四向車作為倉儲系統的主要搬運設備,在提升機的配合下,通過在單層縱橫兩個方向的軌道穿梭可到達立體貨架的任一貨位,執行入庫和出庫作業。

四向車倉儲系統倉庫布局如圖1所示。四向車倉儲系統主要由貨架、輸送機、提升機、緩存區、四向車等組成。貨架具有可以存儲貨物的貨位以及供四向車行走的軌道。輸送機沿y軸方向運動將貨物運至提升機處,提升機不僅可以沿z軸方向運動,也可以沿y軸方向取貨和放貨。四向車通過換向機構實現x軸和y軸方向的運動,在搬運貨物時,四向車的頂升機構將貨物頂起,到達目標貨位后,頂升機構下降將貨物放置在貨位上。

為求解同批多筆出/入庫作業的最優貨位集合,滿足動態作業環境約束的同時使作業能耗最低,對貨位分配優化模型作如下假設:

1)單筆作業只有一個托盤出入庫;

2)模型中將目標貨位與出入庫口之間的曼哈頓距離作為作業搬運距離;

3)四向車倉儲系統所有貨位大小規格相同,最大承載相同;

4)為避免與出入庫口選擇問題耦合,將倉庫出入庫口簡化為一個;

5)對于換層作業,提升機的承載質量只考慮貨物,不考慮四向車自身的質量。

2 貨位分配優化模型

四向車倉儲系統的貨架可以看作一個三維立體高層貨架,貨架規模由貨架的總行數X、總列數Y和總層數Z描述,l、w、h分別表示貨位的長、寬、高,出入庫口的坐標設置為(x0,y0,z0),針對單筆作業q的目標貨位坐標為(xq,yq,zq)。J=(J1,J2,…,Jq,…,Jn)表示單批作業,Jq表示第q筆作業,n表示作業總數。貨位分配優化模型以作業能耗少、貨架重心低和作業分布均衡為優化目標分配貨位。

2.1 減少作業能耗

四向車作業能耗主要由搬運能耗、托盤頂升能耗和轉向能耗組成,提升機作業能耗主要由搬運能耗組成。搬運能耗與作業功率和時間有關,目標貨位的遠近會影響作業時間,載貨質量會影響牽引力的大小,進而影響作業功率。

設備運行可分為啟動加速、勻速行駛、到達減速3個階段,由于設備行程有長短差別,實際作業過程中會出現兩種運動過程:設備可達到最大運行速度vmax;設備未達到最大運行速度vmax。兩種運動過程的設備運行速度-時間曲線圖如圖2所示。

基于圖2所示的速度-時間曲線,可得四向車與提升機的作業能耗計算如表1所示。表1中每種設備要考慮兩種運動過程,當兩種運動過程的計算方法相同時共用同一個計算公式,且設備只有在達到最大運行速度時才會有勻速運動,故未達到最大運行速度的設備在勻速運動時無計算公式。

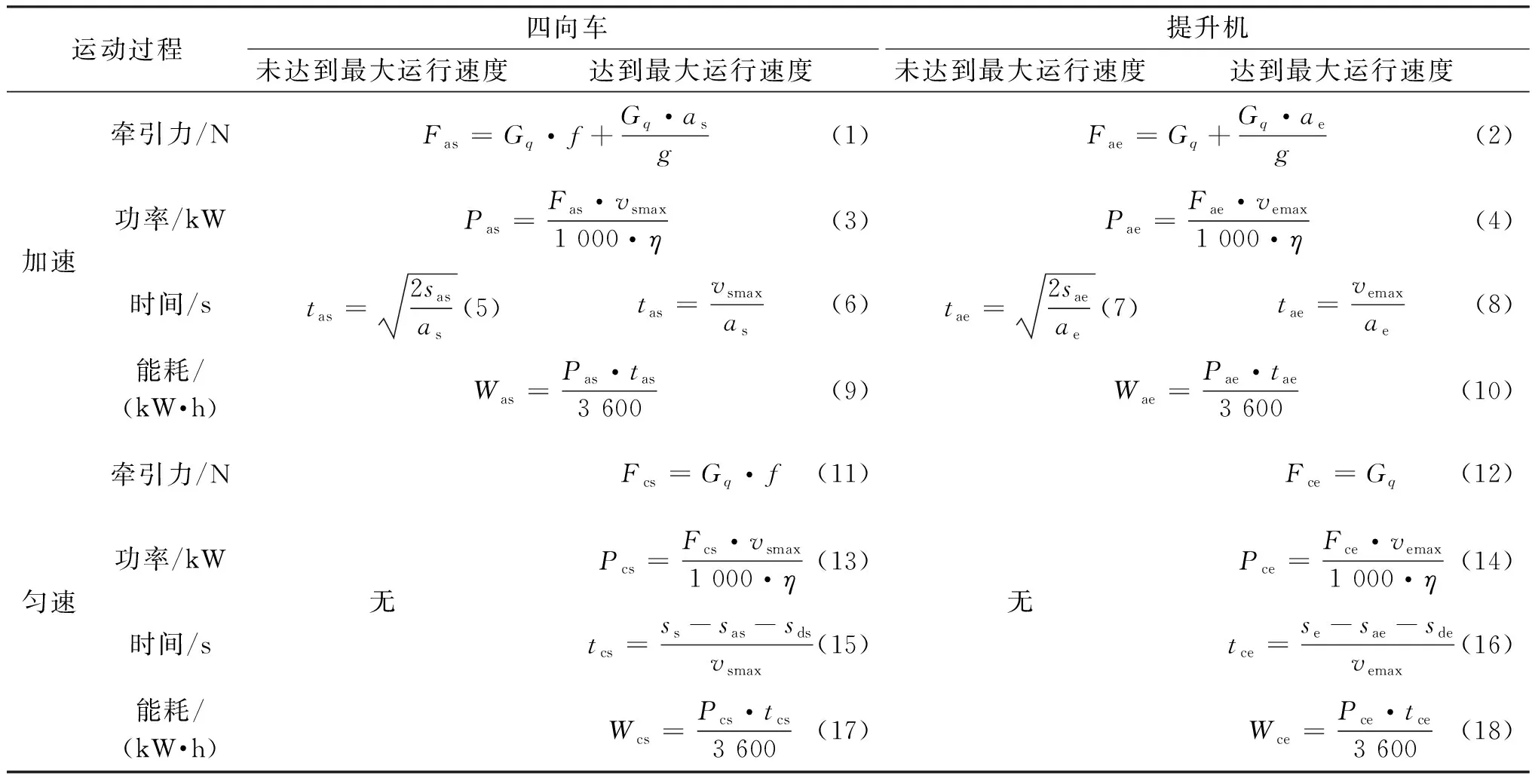
表1 設備搬運能耗計算方法Table 1 Calculation method of equipment handling energy consumption

以四向車為對象研究能耗計算方法。式(1)中Gq為四向車所載貨物受到的重力,f為四向車和軌道之間的摩擦因數,g為重力加速度,as為四向車的加速度,Fas為四向車在加速過程中所受牽引力;式(3)中vsmax為四向車最大運行速度,η為運行效率,Pas為四向車加速運動的功率;式(5)和(6)是根據時間速度曲線和搬運距離得出的兩種搬運時間計算方式,tas為加速運動的時間,式(5)中sas為加速運動位移;式(9)中Was為四向車加速運動的能耗;式(11)和(13)中,Fcs和Pcs分別為四向車勻速運動的牽引力和功率;式(15)中tcs為勻速運動的時間,ss為四向車搬運貨物的總位移,sds為減速運動的位移;式(17)中Wcs為四向車勻速運動的能耗;式(19)中Fds為四向車減速運動所受牽引力;式(21)中Pds為四向車減速運動的功率;減速運動的搬運時間計算方式如式(23)和(24),tds為減速運動的搬運時間;式(27)中Wds為四向車減速運動的能耗。

提升機的運動過程與四向車基本一致。式(2)中ae為提升機的加速度;式(4)中vemax為提升機最大運行速度;式(7)中sae為提升機的加速位移;式(16)中se為提升機的總位移,sde為提升機減速運動的位移。

托盤頂升能耗發生在四向車取放貨物時,四向車需要將承載貨物的托盤從貨位上頂起或放置在貨位上,能耗計算方法如式(29)所示。

(29)

式中:Wqlift為執行作業q時托盤頂升和下降的能耗;dlift為四向車頂升或下降托盤的距離。

四向車將貨物搬運到指定貨位,搬運途中不可避免要做轉向運動,四向車的轉向運動實際上是對不同方向運動輪的頂升運動,故四向車轉向時的能耗計算如式(30)所示。

(30)

式中:Wqturn為執行作業q時轉向的能耗;dturn為四向車換向機構的行程。

根據倉庫布局特點得出貨位分配后目標貨位與出入庫口在x、y、z軸方向的距離分別為

dqx=(xq-x0)·w

(31)

dqy=(yq-y0)·l

(32)

dqz=(zq-z0)·h

(33)

由式(31)～(33)得出的距離可得作業q在x、y和z軸方向的搬運能耗Wqx、Wqy、Wqz如表2所示。

表2 單筆作業搬運能耗計算方法Table 2 Calculation method of energy consumption for single operation

由單筆作業能耗可得單批作業四向車與提升機的總能耗W為

(40)

2.2 降低貨架重心

實際倉儲過程中,應該盡可能地讓質量較大的貨物放置在貨架的低層,從而降低貨物與貨架的整體重心,以保證出入庫作業安全。貨架垂直方向的重心計算如式(41)所示。

(41)

式中:Oz為貨架垂直方向的重心;mxyz為坐標(x,y,z)貨位上的貨物質量。

2.3 均衡作業分布

當多個作業的目標貨位被分配在同一層時,由于該層四向車數量的限制易造成作業堵塞,從而影響整體倉儲效率,因此,在貨位分配時應盡可能使各層的作業數量分布均衡。作業分布均衡度B表示分布在每層的作業數量離散程度,反映作業在層間分布的均衡程度,B值越小,表示作業分布越均衡。B計算如式(42)所示。

(42)

2.4 貨位分配優化模型

由于各個子目標的量綱不同且計算結果的數值大小差異較大,故需要對目標函數進行歸一化處理,具體如下:

(43)

(44)

(45)

Wmax=Wqxmax+Wqymax+Wqzmax,Wmin=0

(46)

Ozmax=Z·h,Ozmin=h

(47)

(48)

(49)

式(43)中Wmax為貨物重量達到貨位承載最大載荷時,目標貨位被分配到離出入庫口在3個方向都達到最遠時的能耗值,Wmin為最小能耗值;式(44)中Ozmax為貨架重心最大值,Ozmin為貨架重心最小值;式(48)中W*、Oz*和B*分別為歸一化后的作業能耗、貨架重心高度和作業分布均衡度;式(49)中Omax為貨位能承載的最大載荷,Aq為作業q的貨位可行域,Aq是實時變化的。當為入庫作業q分配貨位時,Aq是在此時的空貨位集合Semp中去除已經被其他入庫作業占用的貨位集合Sin,即Aq=Semp-Sin。當為出庫作業q分配貨位時,Aq是在滿足當前出庫需求的庫存貨位集合Sinv中去除已經分配給其他出庫作業的貨位集合Sout,即Aq=Sinv-Sout。

在實際出庫作業中,可能會出現庫存貨位上的物料種類或數量無法滿足出庫需求的情況,為了最大限度地為出庫作業分配貨位,每個出庫貨位k引入出庫能力服務系數βk,其計算如式(50)所示。

(50)

式中:S為出庫作業所需物料種類總數;okc為貨位k存有物料c的數量;rkc為貨位k需要物料c的出庫數量。

(51)

由式(51)可知,出庫能力服務系數βk∈[0,1],βk值越大,該貨位的出庫能力越強,βk值越小,該貨位的出庫能力越弱。根據實際倉儲環境,設置βk的最低閾值,系統從數據庫中篩選出高于此閾值的貨位,動態生成出庫貨位可行域。

通過多目標加權建立考慮能耗的貨位優化模型(簡稱“能耗模型”)如式(52)所示,其中,ω1、ω2和ω3分別為W*、Oz*和B*的權重。在面向低能耗的貨位分配優化模型中,主要優化目標是節省設備作業能耗,故為W*子目標分配最大權重。由于降低重心與節能兩個子目標都傾向于把貨物放在較低的貨架層,又因為在貨架可靠性設計時,通常已經充分考慮重心對力學穩定性的影響[19],所以在貨位優化時為Oz*子目標分配較小權重。在W*和Oz*兩個子目標的共同作用下,貨物易被分配在較低層貨位,為避免作業被集中分配在較低層,造成作業堵塞進而降低倉儲效率,為B*子目標分配較大權重。權重大小設置為ω1>ω3>ω2。

FW=min(ω1·W*+ω2·Oz*+ω3·B*)

(52)

為了驗證能耗模型的有效性,引入考慮距離最短的貨位優化模型(簡稱“距離模型”)進行對比,如式(53)所示。

Fd=min(ω4·S*+ω5·Oz*)

(53)

(54)

式中:S*為單批作業的總距離,其計算方式如式(54)所示;ω4和ω5分別為子目標S*和Oz*的權重。距離模型重點對作業距離進行優化,權重大小設置為ω4>ω5。

3 自適應變異差分進化算法

自適應差分進化算法通過自適應調整進化算子提高算法的收斂性能。基于自適應差分進化的貨位優化算法步驟如下所述。

3.1 初始化及編碼

首先進行種群初始化,種群由多個個體向量x組成。個體向量x=(x1,x2,…,xj,…,xn),j為基因在向量內部的索引,基因索引對應作業編號,j∈[1,n],n為個體長度,即作業個數。xj如式(55)所示,每個基因采用0～1的實數編碼。

xj=rand(0,1)

(55)

3.2 解碼

將作業q對應的基因值解碼后可獲得作業的目標貨位(xq,yq,zq),解碼過程如圖3所示,解碼計算方法如式(56)所示。貨位可行域通過對數據庫動態查詢進行更新。

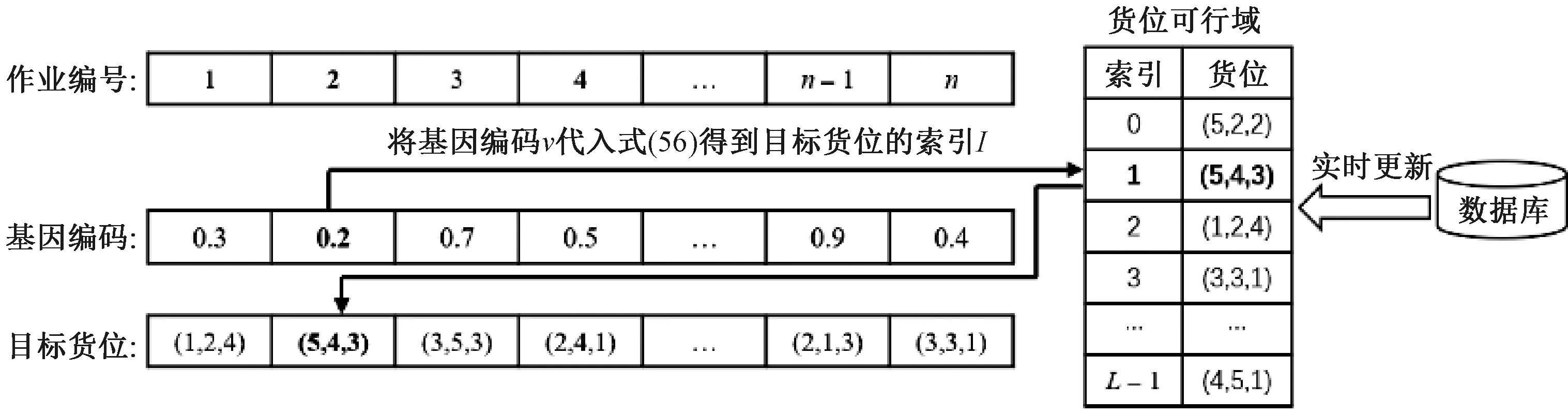
圖3 解碼過程示意圖Fig.3 Decoding diagram

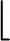
(56)

式中:v為作業對應的基因編碼值;L為貨位可行域中的貨位總數;I為求解貨位在貨位可行域中的索引,索引為向下取整的結果。

當可行域貨位數量L=10,編號為2的作業基因編碼為0.2,經過計算貨位索引I為1,對應于可行域中貨位是(5,4,3)。

3.3 變異

個體變異計算如式(57)所示,自適應產生變異縮放因子F,其由Fi1和Fi2兩部分[20]組成,三者的計算如式(58)～(60)所示。其中:Fi1按時間呈非線性自適應衰減,保證算法前期有較好的全局搜索能力,以及后期有較好的局部勘探能力;Fi2按每個個體自身與種群最優個體目標函數值差異來自適應調整。

(57)

(58)

(59)

(60)

3.4 交叉

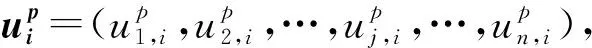
(61)

3.5 選擇

如果試驗向量ui的目標函數值小于等于目標向量xi的目標函數值,那么試驗向量在下一代中取代目標向量,否則目標向量會繼續保持到下一代,選擇操作如式(62)所示。

(62)

4 試驗與分析

為驗證上述模型和算法的有效性,本文使用圖1所示的四向車倉儲系統布局結構為例進行試驗,倉庫規模與生產企業的中小型倉庫規模相仿。用于試驗的倉庫規模、貨位參數、四向車、提升機主要規格參數如表3所示。

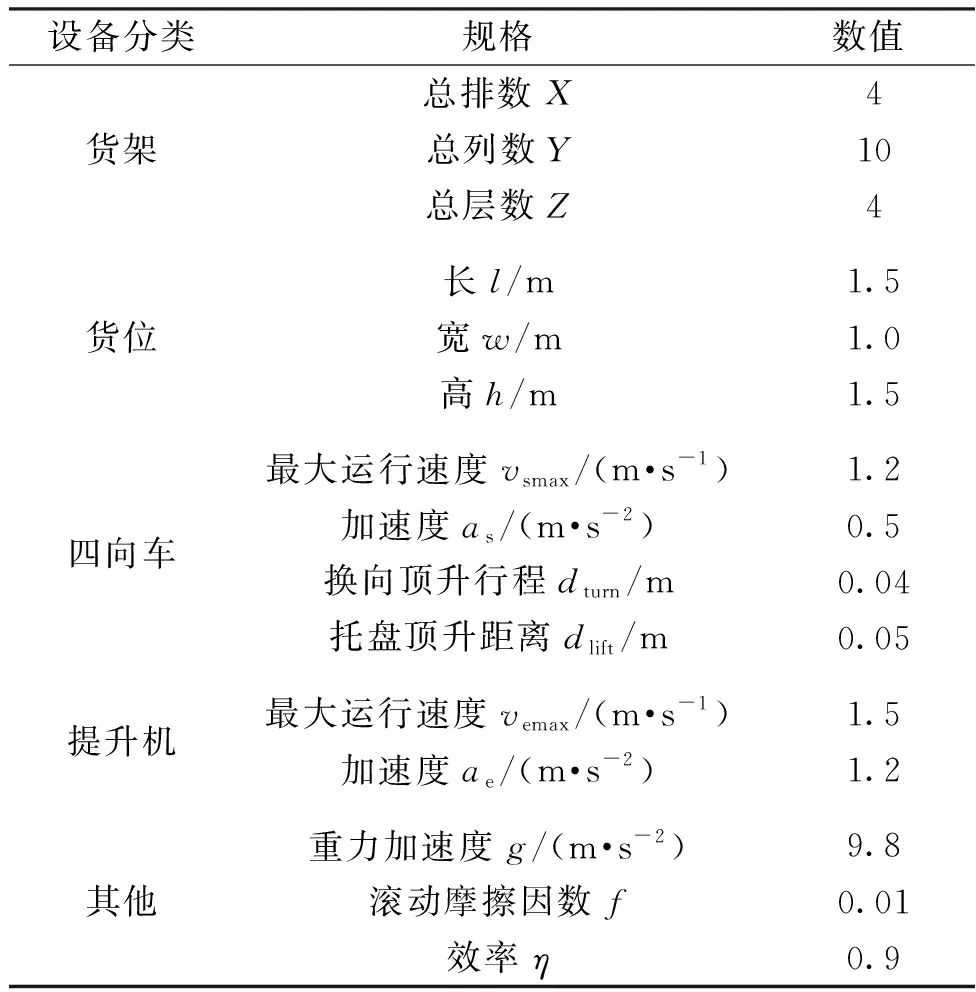
表3 四向車倉儲系統參數

將分別考慮能耗和距離的貨位分配模型進行對比試驗,試驗作業信息如表4所示。試驗計算機基本配置參數為AMD/Ryzen 5 4600U/2.1 GHz/16 GB,操作系統為Windows 10,使用C#編寫算法,Python分析試驗結果。

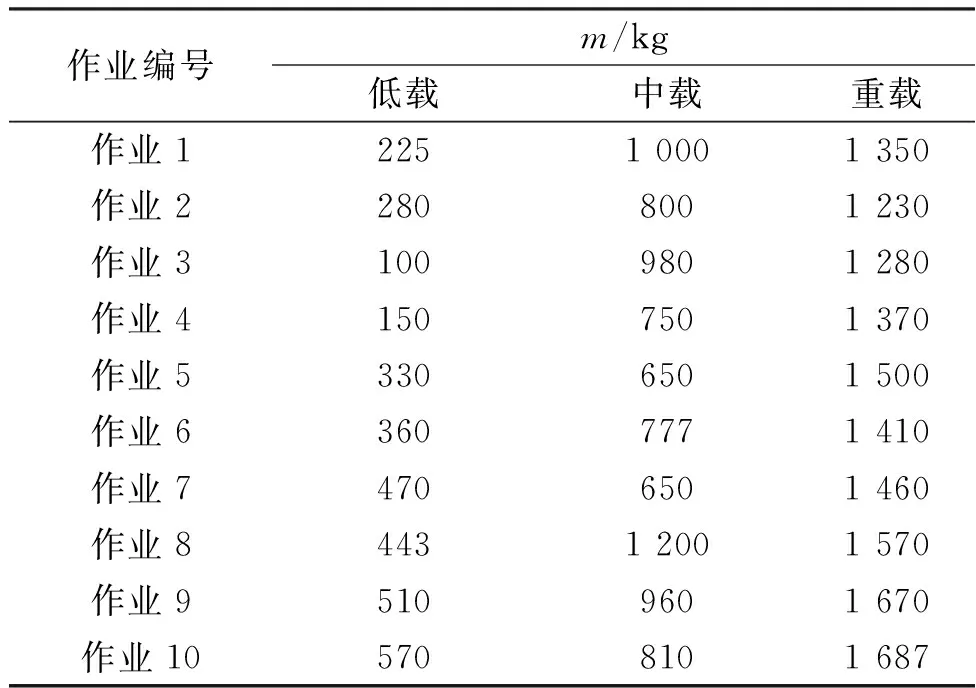
表4 不同載荷的作業信息Table 4 Operation information of different loads

設置3種庫存占有率分別為30%、50%和70%,庫存平均分布在每層和每排。設置3種載荷類型:低載(m<600 kg)、中載(600 kg≤m≤1 200 kg)、重載(m>1 200 kg),每種載荷類型隨機生成10筆作業。兩個模型在不同庫存規模和不同載荷類型情況下各進行兩組試驗,每組試驗測試8次,每次試驗10筆作業。差分進化算法的最大迭代次數為500,初始種群規模為50,變異參數自適應變化范圍為0.1～0.5,交叉概率為0.5。經過多次試驗對結果進行分析并調整權重,最終設置能耗模型的子目標權重比為ω1∶ω2∶ω3=3∶1∶2,距離模型的子目標權重比為ω4∶ω5=4∶1。

選擇不同庫存情況下兩組試驗中綜合目標函數值最低的一組試驗為例,貨位分配結果如圖4所示,其中,綠色標識為預設庫存,橙色標識為貨位分配結果。貨位分配優化求解的迭代曲線如圖5所示。

圖5 不同模型的貨位分配優化求解迭代曲線Fig.5 Iterative curve for optimal solution of storage allocation for different models

由圖5可知,能耗模型在庫存占有率為30%、50%、70%條件下求解出貨位分配結果所需要的迭代次數分別為66、85、95,而距離模型需要的迭代次數分別為196、176、189,顯然能耗模型的求解速度優勢明顯。

統計不同庫存規模下2種模型的試驗結果,并計算得出各目標的平均值如表5所示,表中數據經過歸一化處理,故沒有量綱。在3種不同庫存條件下,能耗模型求解8次試驗所需的平均迭代次數分別為70、87和88,距離模型需要的迭代次數分別為141、138和155。能耗模型在求解速度方面普遍較優,至多可以提高50%。

表5 不同庫存規模兩種模型的試驗結果Table 5 Experimental results of two models with different inventory sizes

由表5可知,能耗模型在不同庫存規模下的重心高度全部小于距離模型下的重心高度,因此前者貨架更穩定。

由表5可知,在3種庫存規模下能耗模型和距離模型的作業分布都比較均衡,可以有效避免作業過于集中于某一層而造成作業堵塞。能耗模型在節能降耗的同時,兼顧了作業均衡。

不同庫存規模下,能耗模型與距離模型相比,前者搬運距離分別增加了6%、4%和4%,即搬運效率有所下降,而在總體能耗方面,即同時考慮提升機和四向車的作業能耗,總能耗分別節約了12%、10%和14%。由此可見,在搬運效率稍微下降的情況下,能耗模型節能顯著。

在四向車能耗方面,由于四向車受到自身電池電量的限制,作業一段時間后需要進入倉庫中的充電位充電,由于充電位數量有限,可能會出現四向車排隊充電進而堵塞交通的情況,這將影響倉庫整體的作業效率。減少四向車的作業能耗,可以降低充電頻次,節省充電位資源。由表7可知,在3種不同的預設庫存規模下,能耗模型與距離模型相比,前者四向車執行同批作業分別節能7%、7%和5%左右。

預設庫存規模為50%,在3種不同載荷類型下進行試驗,試驗結果如表6所示。

表6 不同載荷類型兩種模型的試驗結果Table 6 Experimental results of two models with different load types

由表6可知,不同載荷類型下,與距離模型相比,能耗模型在總體節能和求解效率方面具有明顯優勢,在降低重心和四向車節能方面繼續保持優勢,兩者的作業分布都較均衡。綜上所述,對于不同質量分布的作業,能耗模型都可以合理有效地分配貨位。

5 結 語

針對四向車式密集倉儲系統的貨位分配問題,提出一種面向低能耗的貨位分配優化模型以及自適應的差分進化求解算法。經過仿真試驗得出,上述模型及算法在減少倉儲能耗與提高求解效率兩方面均具有顯著優勢,對促進綠色、節能、高效倉儲具有積極意義。

實際倉儲作業能耗與搬運設備的路徑規劃、作業調度密切相關,綜合考慮貨位決策、設備路徑規劃及作業調度的倉儲節能降耗問題有待進一步研究。