考慮可靠性成本的配電網多階段擴展規劃方法

張軍達,盧姬,常俊曉,廖小兵

(1.國網浙江綜合能源服務有限公司,杭州 310016; 2.國網浙江臺州供電公司,浙江 臺州 318000;3.武漢工程大學 電氣信息學院,武漢 430205)

0 引 言

現有的供電中斷90%以上是由配電系統引發的,因此,從配電網規劃層面上考慮可靠性約束對提升供電可靠性至關重要[1-2]。在規劃層面考慮可靠性約束是通過權衡投資成本與可靠性水平提升之間的關系來實現配電網最優擴展規劃。這樣一方面可以減少用戶供電中斷未提供電能而造成的損失;另一方面在供電可靠性較差的情況下減少相應的考核懲罰,即在供電可靠性較高時可以獲得相應的考核獎勵[3],而在供電可靠性較低時需要付出懲罰成本。

為了量化可靠性的經濟效益,即可靠性價值,必須量化配電網的可靠性水平。為此,配電網采用了多種可靠性評估指標[4-5],其中系統平均停電持續時間指標(SAIDI),系統平均停電頻率指標(SAIFI)和系統缺供電量期望(EENS)這三類指標使用最多[6]。SAIDI,SAIFI和EENS這三類指標通常使用模擬法去逐個分析每個故障事件對系統和用戶停電的影響,逐個模擬所有元件故障的影響,這種方法一方面耗時,另一方面無法實現可靠性指標的顯式表達,即建立元件故障參數與可靠性指標之間的顯式關系[7]。這也是基于模擬法的可靠性指標難以嵌入到配電網擴展規劃模型中的重要原因,因此,已有文獻采用迭代方法,即先假設網絡拓撲結構已知,然后校驗可靠性指標,進而改進配電網規劃。主要是采用啟發式的智能優化算法,比如文獻[8]中的遺傳算法,文獻[9]中的非支配排序遺傳算法等。然而,采用啟發式算法求解考慮可靠性約束的配電網擴展規劃模型,難以保證規劃模型的收斂性和最優性,會造成一定的經濟性或可靠性損失。

為了克服模擬法評估可靠性的弊端,基于解析法的配電網可靠性評估方法應運而生。文獻[10]基于節點相關信息的等值遞推關系,提出了代數模型的可靠性指標計算方法;文獻[11]采用層次聚類方法對典型饋線進行識別和聚類,通過回歸分析導出了每種典型饋線拓撲下可靠性指標的顯式公式。文獻[12]建立了基于拓撲變量的混合整數線性優化模型的可靠性指標評估方法。這些非模擬法的配電網可靠性評估方法從根本上避免了多次模擬的思路。在此基礎上,文獻[13]將影響可靠性的網絡拓撲轉化為優化模型,建立了同時考慮經濟性和可靠性的配電網多階段擴展規劃的混合整數線性優化模型。文獻[14]將面向可靠性的成本納入到配電網擴展規劃模型中,建立了一組混合整數線性方程來計算最常見的配電網可靠性指標。文獻[15]通過將可靠性指標計算過程解析化,并嵌入到配電網擴展規劃模型中,可以精確考慮故障隔離、負荷轉供和恢復策略,基于線性化潮流,該配電網擴展規劃模型是一個混合整數線性優化問題,可以高效求解。文獻[16]建立了交直流混合配電網的可靠性顯式表達模型,提出了一種考慮可靠性成本的交直流混合配電網混合整數線性規劃模型。然后,這些文獻對可靠性成本的建模均不夠全面,要么以系統缺供電量期望造成的損失作為可靠性成本,缺少對系統平均停電持續時間指標和系統平均停電頻率指標的考慮。

在此基礎上,文中提出了考慮可靠性成本的配電網多階段擴展規劃方法。首先在可靠性成本方面,不僅考慮了系統缺供電量造成的收入損失,而且基于可靠性激勵率,建立了系統平均停電頻率指標和系統平均停電持續時間指標的相關可靠性成本,其次,采用圖論知識建立了顯式的可靠性指標評估模型,最后形成了考慮可靠性成本的配電網多階段擴展規劃的混合整數線性優化模型,適用于商業求解器求解。在四個算例系統上的仿真結果驗證了本文所提出方法的有效性和擴展性。

1 可靠性約束的配電網擴展規劃模型

傳統的配電網擴展規劃的目標是使得變電站和饋線的投資成本、系統運行成本最小化,以滿足不斷增長的負荷需求[17-18]。而考慮可靠性約束配電網可靠性評估依賴于以下假設:

1)僅考慮由于單條支路停電而導致的持續停電,影響支路停電的特征量是故障率和停電持續時間;

2)考慮三相平衡的輻射狀或網狀配電網,其中連接到變電站的每條支路都配備了斷路器,在變電站的輸出端沒有重合閘。此外,所有支路都配備了一個開關,以進行故障隔離,即隔離故障下游部分,以滿足非故障部分的負荷需求。因此,一旦發生持續故障,故障上游的第一個斷路器就會跳閘,從而減少了所有下游負荷需求。隨后,通過操作開關和斷路器重構網絡拓撲,以減少停電負荷。為此,打開故障上游的第一個開關以隔離故障,然后關閉斷路器,以便恢復斷路器和開關之間所有負荷的電源。最后,一旦隔離故障被清除,相應的開關閉合,并重新恢復供電。

因此,負荷節點受到兩種類型停電的影響:修復和切換停電,在修復損壞之前不會恢復供電;僅切換停電,這與為清除故障組件而實施的網絡重構有關。

圖1給出了所提出的可靠性約束的配電網擴展規劃方法流程圖,通過線性化的潮流模型,建立的可靠性約束的配電網擴展規劃模型是一個混合整數線性優化模型,可以通過商業求解器直接求解。

1.1 目標函數

建立的可靠性約束的配電網多階段擴展規劃的目標是最小化系統總成本,包括投資成本,運行成本以及可靠性成本,如式(1)所示:

(1)

式中t為規劃階段;T為規劃階段總數;r為利率;Invt,Opt分別為t階段的投資成本和運行成本;RRCt為t階段的可靠性成本。

t階段的投資成本包括新建饋線、更換現有饋線、建造或擴建變電站以及增加變電站變壓器的投資成本,如式(2)所示:

(2)

式中l為饋線索引;k為方案編號;LN為新增的饋線集合;Kl為饋線l的投資方案集合;rrk為方案k的資本回收率;CCl,k為饋線l方案k的施工成本系數;xl,k,t為t階段饋線l投資方案k的0-1決策變量;RCl,k為饋線l方案k的更換成本系數;n為節點編號;ΩS為變電站節點集合;rrn為節點n處變電站中除變壓器以外的資本回收率;ECn為節點n處新變電站建設成本系數或現有變電站擴建成本系數;ICn,k為節點n處變電站變壓器方案k的投資系數;xn,t為階段t節點n處新建變電站或擴建變電站的0-1決策變量;xn,k,t為階段t節點n處變電所變壓器方案k的0-1決策變量。

其中資本回收率定義為rrk=r(1+r)ULk/[(1+r)ULk-1],?k∈Kl∪Kn,ULk為方案k使用壽命和rrn=r(1+r)ULn/[(1+r)ULn-1],?n∈ΩS,ULn為節點n處變電站中除變壓器以外的設備使用壽命。

t階段的運行成本包括饋線的運行成本、變電站變壓器的維護成本以及變電站的電力成本,如式(3)所示:

(3)

式中LF、LR分別為現有的饋線集合、現有的可更換饋線集合;OCl為現有饋線l的運行成本系數;yl,t為t階段是否使用現有饋線l的0-1決策變量;OCl,k為饋線l方案k的運行成本系數;yl,k,t為t階段饋線l的方案k是否使用的0-1決策變量;Kn為節點n處變電站變壓器的投資方案;MCn,k為節點n處變電站變壓器方案k的維護成本系數;τ表示階段;b為負荷持續時間曲線分塊的索引;LD為負荷持續時間曲線的分塊集合;pf表示系統功率因數;Δb為負荷塊b的持續時間;Prn,b,t為在階段t節點n處負荷塊b的電價;gn,b,t表示節在t階段點n處變電站的負荷塊b注入電力。

最后,t階段的可靠性相關成本基于以下因素建模:在網絡故障期間未向負荷提供電能而造成的電費損失;可靠性指標的激勵成本,如式(4)所示:

(4)

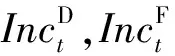
其中預期電費損失RLt為:

RLt=ERtEENSt?t∈T

(5)

式中ERt為t階段的每單位電能的預期收益;EENSt為在t階段未提供的預期電量。

與可靠性指標相關的激勵成本采用式(6)～式(7)計算:

(6)

(7)

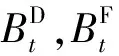
式(6)～式(7)分別基于系統平均停電持續時間指標和系統平均停電次數指標進行線性激勵來建立可靠性成本模型。因此,當可靠性指標小于相應的基準值,即產生獎勵效益,否則為懲罰成本。

1.2 投資0-1決策變量約束

投資決策受以下約束:

(8)

(9)

(10)

(11)

xl,k,t∈{0,1} ?l∈LR∪LN,?k∈Kl,?t∈T

(12)

xn,t∈{0,1} ?n∈ΩS,?t∈T

(13)

xn,k,t∈{0,1} ?n∈ΩS,?k∈Kn,?t∈T

(14)

式(8)～式(10)規定了在規劃期內,只允許進行一項投資。式(11)是為了防止在相應變電站擴建之前安裝新的變電站變壓器。

對饋線利用變量約束為式(15)～式(21):

yl,t=1; ?l∈LFLSW,?t∈T

(15)

(16)

(17)

(18)

(19)

yl,t∈{0,1}; ?l∈LF∪LR,?t∈T

(20)

yl,k,t∈{0,1}; ?l∈LR∪LN,?k∈Kl,?t∈T

(21)

式中LSW表示節點集合L中包含正常運行下可切換的饋線集合。

式(15)～式(17)通過饋線利用變量設置在正常運行下不可切換狀態,因此不能用于網絡重構;現有的不可切換饋線在所有階段都可用,因此它們的利用率變量必須等于1,如式(15)所示。在進行任何更換操作之前,必須使用現有的可更換饋線部分,如式(16)所示。最后,根據式(17)的規定,從進行相應投資的階段開始,必須使用可更換和新增饋線。

與式(16)和式(17)類似,式(18)和式(19)通過可更換和新增饋線利用變量設置為可切換狀態,因此可用于網絡重構。這些約束通過將饋線利用變量設置為0來避免使用網絡中未安裝的饋線部分選項。另一方面,對于已安裝的選項,式(18)～式(19)對饋線利用變量沒有限制,因此這些選項可用于優化網絡的配置。

1.3 系統運行約束

系統運行受到式(22)～式(29)中定義的各種約束:

(22)

(23)

M(1-yl,t); ?l∈LF∪LR,?b∈LD,?t∈T

(24)

(25)

(26)

(27)

(28)

(29)

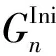
采用文獻[19]中線性化潮流模型,負荷節點和變電站節點的功率平衡分別由式(22)～式(23)確定。式(24)～式(25)對各種類型的支路潮流進行建模。式(26)～式(28)分別對現有和新增饋線的變電站注入功率和流過的有功功率流施加了限制。節點電壓的下限和上限在式(29)中約束。

1.4 輻射狀拓撲約束

本小節利用圖論[20]知識在配電網擴展規劃模型中施加輻射狀拓撲約束。根據圖論知識,如果節點數等于支路數加1,則連接圖沒有環路,這一結論可以擴展到一個圖,該圖由沒有環路的連接子圖不相交聯合組成,其節點數等于支路數加上子圖數。首先,在每個階段,可能會隔離多個節點,因此不應計算在內;其次,網絡的子圖數量等于現有變電站的數量,因為每組連接的負荷節點必須由單個變電站供電。根據圖論這一結論,現有饋線的數量等于連接節點的數量(即連接的負荷節點數加上連接的變電站節點的數量)減去子圖的數量。由于連接的變電站節點數等于子圖的數量,如果在運行的饋線的數量等于連接的負荷節點的數量,則可以確保輻射狀運行。

這種基于圖論的輻射狀拓撲約束如式(30)～式(36)所示:

ul,t=yl,t; ?l∈LF,?t∈T

(30)

(31)

(32)

0≤ul,t≤M|dl,t|; ?l∈L,?t∈T

(33)

ul,t≤LPMn,t;?n∈ΩD, ?l∈L|χn,l≠0|,?t∈T

(34)

LPMn,t≤1; ?n∈ΩD,?t∈T

(35)

(36)

式中dl,t為在階段t饋線l下游的平均負荷需求;L為所有饋線集合;ΩD為負荷節點集合;LPMn,t是一個0-1變量,如果節點n在階段t至少連接到一個饋線,則等于1,否則為0;ul,t是一個0-1變量,如果t階段饋線l在運行,t等于1,否則為0。

式(30)～式(32)分別為現有的固定饋線、現有的可更換饋線和新的饋線建立的ul,t模型。根據式(33),對于未使用的饋線,變量ul,t設為0。式(33)中,dl,t為t階段通過饋線l的平均負荷需求,由于缺乏對網絡拓撲的預知,因此使用絕對值。對于非隔離節點,即對于與之連接的至少一個支路的利用變量ul,t為1的節點,根據式(34)～式(35)將LPMn,t設為1。另一方面,對于那些沒有任何連接的支路處于運行狀態的節點,式(34)～式(36)將LPMn,t設為0。對于此類節點,式(34)～式(35)確保LPMn,t取小于或等于1的非負值。最后,式(36)考慮到無環路連通圖的支路數最少,則只有在每個孤立節點LPMn,t等于0的情況下才能滿足式(36)。

2 顯式可靠性指標計算方法

本節闡述如何顯式計算三類常用的配電網可靠性指標,即系統缺供電量期望,系統平均停電持續時間指標和系統平均停電次數指標。與已有文獻相比,文中所提出的顯式可靠性指標計算方法具有以下三個特點:1)通過額外的二進制變量和新的非線性表達式考慮了網絡資產的投資決策;2)通過在虛構系統上施加KCL來表征變電站可用性;3)可靠性指標的混合整數非線性表達式的等效線性化。

2.1 EENS

EENS量化了由于網絡故障而未提供的期望電量,可以表示為由于每個饋線部分故障而減少的供電量的總和,如式(37)所示:

(37)

式中BEENSl,t為在階段t饋線l的未提供預期電量。

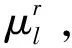
(38)

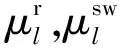
對于現有的可更換和新添加的饋線段部分,每個選項k的故障率和維修時間各不相同。因此,在式(39)和式(40)中分別使用二進制利用率變量來表征可更換和新添加的饋線部分的可靠性參數:

(39)

?l∈LN,?t∈T

(40)

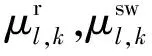
為了得到每個饋線下游的總負荷需求,即dl,t,將KCL應用于一個虛構的相同拓撲結構的無損網絡,其節點負荷等于年平均節點負荷需求,如式(41)～式(44)所示:

(41)

(42)

-Mul,t≤dl,t≤Mul,t; ?l∈L,?t∈T

(43)

(44)

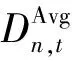
式(41)～式(42)分別建立了虛擬網絡負荷節點和變電站節點的功率平衡方程。式(43)～式(44)將未利用饋線的虛擬功率和未利用變電站的虛擬電量均設為0。

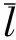
(45)

(46)

(47)

(48)

δl,t=0; ?l∈SL,?t∈T

(49)

為了說明式(41)～式(49)的過程,以圖2所示的簡單網狀結構表示給定時間階段t的投資計劃。可以看出,該網絡有兩個變電站節點,三個平均負荷需求都等于1 MW的負荷節點,以及六個饋線,其中三個直接連接到變電站節點,因此,L={l1-l6}和SL={l1,l4,l5}。圖2還顯示了兩種可能的輻射狀網絡拓撲,稱為輻射狀拓撲1和輻射狀拓撲2。如圖2所示,每個饋線的第一個饋線部分甚至饋線的數量都依賴于拓撲結構。

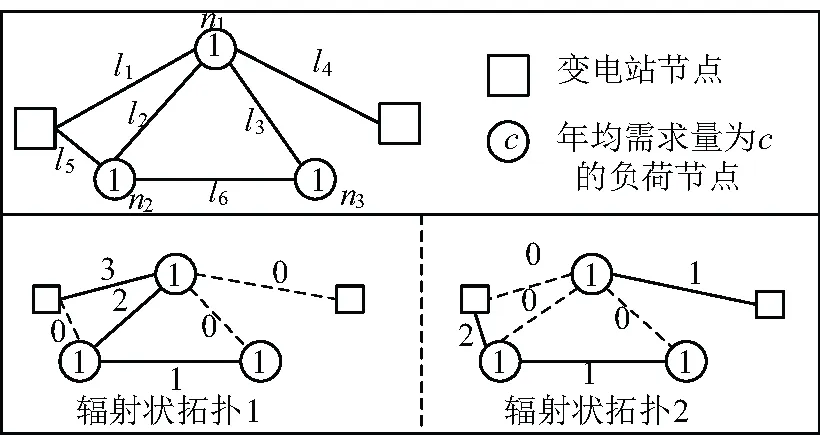
圖2 兩種可能的輻射狀拓撲的饋線虛擬功率

對于圖2中的兩種輻射狀拓撲,虛構功率dl,t由式(41)～式(44)得到的結果顯示在相應的饋線旁邊。可以看出,每個饋線的第一饋線部分的虛擬功率等于該饋線的總負荷需求。

δl6,t=zl6,l1,t(|dl1,t|-|dl6,t|)+zl6,l4,t(|dl4,t|-|dl6,t|)+zl6,l5,t

(|dl5,t|-|dl6,t|)=1×(3-1)+0×(0-1)+0×(3-1)=2

這等于饋線l6上游的總負荷需求。類似地,對于輻射狀拓撲2中的饋線zl6,l5,t=1和zl6,l1,t=zl6,l4,t=0,因此,由式(48)可得:

δl6,t=zl6,l1,t(|dl1,t|-|dl6,t|)+zl6,l4,t(|dl4,t|-|dl6,t|)+zl6,l5,t

(|dl5,t|-|dl6,t|)=0×(0-1)+0×(0-1)+1×(2-1)=1

(50)

(51)

(52)

此外,式(39)線性化為:

M(1-yl,t); ?l∈LR,?t∈T

(53)

M(1-yl,k,t); ?l∈LR,?k∈Kl,?t∈T

(54)

-M(1-yl,k,t); ?l∈LR,?k∈Kl,?t∈T

(55)

式(53)～式(54)當yl,t=0和yl,k,t=0失效,因為式(53)～式(54)的右側變為較大的負值。因此,根據式(55),BEENSl,t的下限為0。相反,當yl,t=1和yl,k,t=1,式(53)和式(54)分別將BEENSl,t的下界設置在式(39)的右邊。

同理,式(40)和式(48)線性化為:

(56)

(57)

2.2 SAIDI

SAIDI表征配電網用戶的平均年停電持續時間。饋線l在階段t故障引起的全年用戶停電總時間表示為BIDIl,t,SAIDI指標可以表示為:

(58)

式中BIDIl,t為在階段t饋線l故障導致停電戶中斷時間;Nn,t為在階段t連接到節點n的用戶數。

式(59)～式(61)的模型BIDIl,t適用于各種類型的饋段。這些表達式分別與式(38)～式(40)相同,其中hl,t和ηl,t分別起到dl,t和δl,t的作用。

?l∈LF,?t∈T

(59)

(60)

?l∈LN,?t∈T

(61)

式中ηl,t為t階段連接到饋線l的上游節點的用戶數量;hl,t為t階段饋線l下游節點連接的用戶數。

為了獲得hl,t,即t階段饋線下游節點連接的用戶數,將KCL應用于一個虛構的相同拓撲的無損網絡,其節點負荷需求等于連接的用戶數,如式(62)～式(65)所示:

(62)

(63)

-Mul,t≤hl,t≤Mul,t; ?l∈L,?t∈T

(64)

(65)

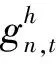
最后,與式(48)～式(49)類似,在t階段連接到饋線l上游節點的用戶數量ηl,t表示為:

(66)

ηl,t=0; ?l∈SL,?t∈T

(67)

2.3 SAIFI

SAIFI指標表征配電網用戶每年的平均停電次數。由于SAIFI與SAIDI的結構相似,其模型可以很容易地推導出,如下所示:

(68)

BIFIl,t=αlλl(|hl,t|+ηl,t); ?l∈LF,?t∈T

(69)

(70)

?l∈LN,?t∈T

(71)

式中BIFIl,t為在階段t饋線l故障導致的用戶停電次數;λl,k為饋線l方案k的單位長度的故障率。

式(68)～式(71)分別類似于式(58)～式(61),其中BIFIl,t與BIDIl,t類似。采用上述線性化方法同樣可以式(68)～式(71)等效線性化。

3 算例分析

采用24節點、54節點、86節點和138節點四個算例系統來驗證所提出的配電網擴展規劃模型的有效性,詳細數據見附錄鏈接:https://pan.baidu.com/s/11B0_g7WUJsp3TKtnPLJnqw pwd=by4x,提取碼:by4x。其中可靠性SAIDI和SAIFI的激勵率分別為0.5和0.15,基準值分別為3.5和1;在Matlab2019Rb下調用CPLEX 12.6求解混合整數線性規劃模型。在24節點和54節點算例系統中,最優間隙設置為e-7,在86節點和138節點算例系統中,最優間隙設置為e-2,這確保了在獲得高質量近似最優解的同時保證算法的收斂。

3.1 24節點系統

24節點系統包括了20個負荷節點、4個變電站節點和33條饋線,其中2條是現有的固定饋線,2條是現有的可更換饋線,29條是候選的待建饋線。在測試中考慮了四類饋線投資方案和兩種變電站變壓器投資方案,規劃周期分為三個階段,所有饋線都是可切換的。

表1給出了采用傳統迭代法和本文所提出的方法的24節點系統規劃結果。其中,傳統迭代法是在規劃結果出來后進行驗證可靠性得出的可靠性相關成本和和總成本。從表1中可以看出,與投資成本和運行成本相比,由于未提供的電能而造成的收入損失可以忽略不計。因此,這種收入損失本身并沒有為配電網提供足夠的動力來提高系統可靠性。因此,對于傳統迭代法,規劃周期內可靠性指標的平均值較高,可靠性水平較低。

表1 24節點系統規劃結果

對于所提出的考慮可靠性成本的配電網擴展規劃模型,可靠性激勵增加了對網絡資產的投資,以產生更可靠的網絡。因此,由此可靠性指標得到了顯著改善。值得一提的是,基于SAIDI和SAIFI的可靠性成本的負值反映了配電網可靠性指標低于相應基準值而獲得的獎勵。因此,與傳統的迭代法相比,本文所提出的考慮可靠性成本的配電網擴展規劃模型的總成本降低了3.47%。

圖3和圖4分別描繪出了傳統迭代法和本文方法在規劃周期第三階段生成的網絡拓撲。圖3～圖4中還顯示了投資決策的類型和時間。除了與投資成本和運行成本相關的拓撲差異外,從圖3～圖4中可以看出,傳統迭代法采用候選項A1和A2,而本文所提出的考慮可靠性成本的配電網擴展規劃模型采用更可靠但更昂貴的候選方案A3和A4。

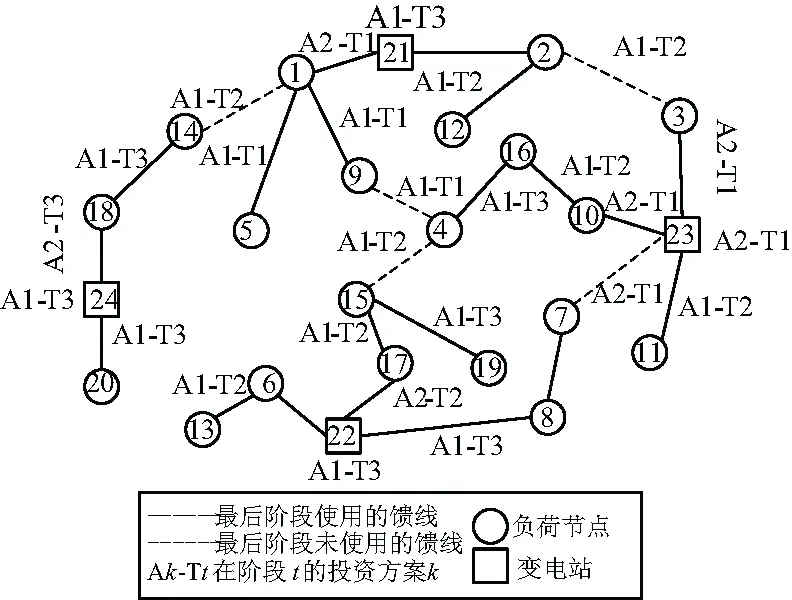
圖3 24節點系統最后階段的拓撲結構(傳統迭代法)

圖4 24節點系統最后階段的拓撲結構(本文所提出的方法)

為了分析可靠性激勵對考慮可靠性成本的配電網規劃結果的影響,進一步總結了不同激勵率下配電網可靠性指標、各項成本的變化情況。為此,假設系統平均停電持續時間指標和系統平均停電次數指標的激勵率乘以0～2之間的比例因子,步長為0.5。圖5顯示了系統平均停電持續時間指標、系統平均停電頻率指標和系統缺供電量期望值隨激勵率的變化情況。圖6顯示了兩種可靠性激勵方的凈獎勵的最終值、投資成本和運營成本的增加量,以及總成本增量隨激勵率的變化情況。如圖5所示,隨著激勵率的增大,配電網可靠性指標下降,供電可靠性提升。然而,從圖6中不難發現,只有相對較小的激勵率投資才能提升可靠性,這是由于可靠性提升的增量成本低于增量收益。

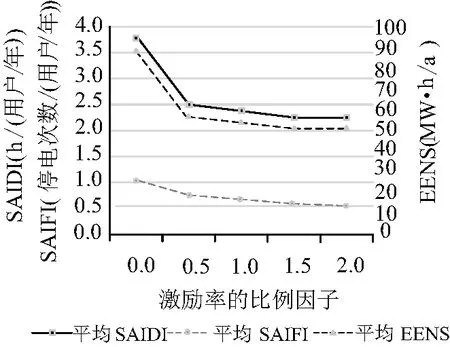
圖5 不同激勵率對可靠性指標的影響

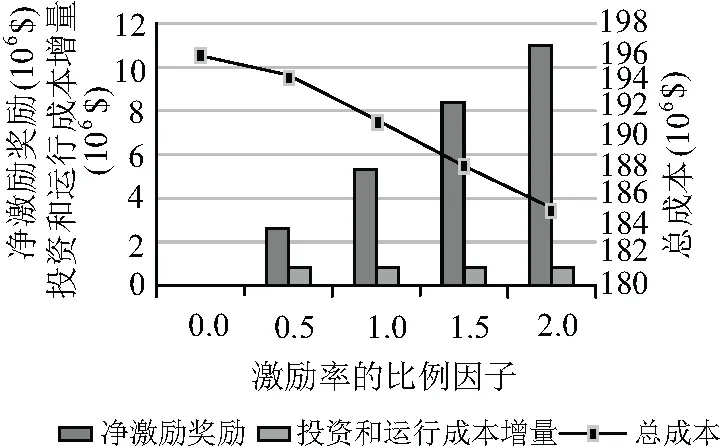
圖6 不同激勵率對系統各項成本的影響

3.2 54、86和138節點算例系統

為了分析所提方法的適用性,進一步在54節點、86節點和138節點三個較大的算例系統上進行仿真分析。54節點系統由50個負荷節點,4個變電站節點和63條饋線組成,包括9個現有的固定饋線,8條現有的可更換和46條候選饋線。86節點系統和138節點系統均由3個變電站節點組成,86節點系統通過94條饋線提供83個負荷節點,138節點系統有135個負荷節點和151條饋線。三個算例系統規劃都考慮十個階段。

表2給出了54、86、138節點系統規劃結果。應當指出,基于系統平均停電持續時間指標和系統平均停電頻率指標的可靠性成本的正值表明可靠性指標比基準值差,因此受到了處罰。另一方面,這些可靠性成本負值,例如86節點和138節點系統,通過達到低于(優于)相應基準的可靠性指標而獲得的獎勵。同樣,由于三個算例系統未向用戶提供電能而造成的收入損失相對而言微不足道,這表明該可靠性指標不能充分激勵可靠性提升的投資。這一結果證明了可靠性激勵在保證配電網可靠性水平方面的重要意義,而不是單純的考慮未向用戶提供電能而造成的收入損失。

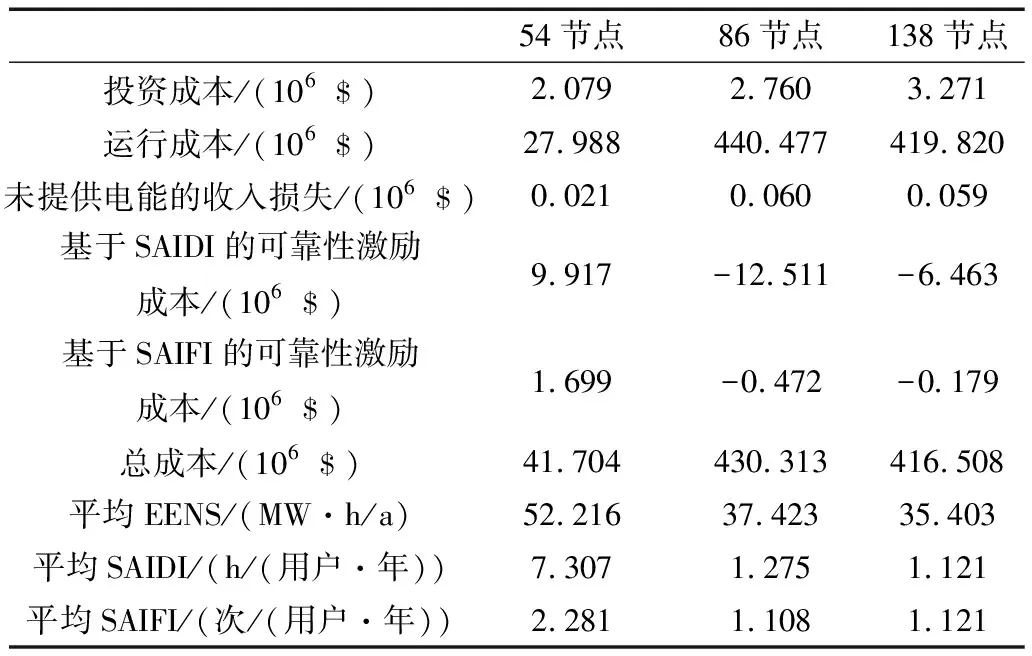
表2 54,86,138節點系統規劃結果

在計算效率方面,采用所提出的方法求解54節點系統、86節點系統和138節點系統分別需要9.10 h、0.17 h和5.65 h,這證實了所提出方法的高效性。

4 結束語

建立了常用的配電網可靠性指標(系統平均停電持續時間指標、系統平均停電頻率指標和系統缺供電量)的顯式評估模型,并將其相關的可靠性成本納入到配電網多級擴展規劃模型中,提出了考慮可靠性成本的配電網多階段擴展規劃的混合整數線性優化模型。在四個算例系統上的仿真結果表明:

1)與投資成本和運行成本相比,由系統缺供電量造成的收入損失可以忽略不計,因此,系統缺供電量這個可靠性指標的提升對規劃結果沒有影響;

2)隨著激勵率的增大,配電網可靠性指標下降,供電可靠性提升;此外,只有合理的激勵率投資才能提升可靠性。