改進量子遺傳算法在含分布式電源配電網中的應用
張雅婷,郭亮,郭達,李乾,劉保安
(1.國網太原供電公司,太原 030012; 2.國網石家莊供電公司,石家莊 050000)
0 引 言
配電網位于電力系統的末端,其供電可靠性和質量不僅關乎企業的經濟效益,而且具有巨大的社會效益[1]。但隨著人口的快速增長,供電系統面臨越來越大的壓力和頻發的故障。這些障礙嚴重影響了電網的安全。據不完全統計,目前80%以上的停電是由配電系統故障引起的。這些故障嚴重影響了電網的安全[2],需加強電力系統安全分析,尤其是配電網故障分析和定位。
隨著智能配電網技術的發展,國內外配電網的定位技術主要分為主動定位法和被動定位法。主動定位法通過向故障線注入檢測信號實現故障定位,被動定位法根據傳輸線本身的電流和電壓信號實現故障定位。在文獻[3]中,提出了一種基于π型線的等效模型,并使用內部電阻電壓源代替了并網分布式電源。考慮到過渡電阻不消耗無功功率,建立故障定位方程,并結合同步測量數據得到故障測距。在文獻[4]中,提出了一種基于遺傳算法的配電網故障定位方法,應用較為成熟,但算法局部搜索能力較差和后期搜索效率低。在文獻[5]中,將粒子群優化算法和矩陣算法相結合,對配電網進行故障定位。該方法首先找到故障線,然后確定故障點的確切位置。在文獻[6]中,提出一種結合粒子群優化算法和差分進化算法用于配電網的故障定位。該算法首先對二元系統的故障信息進行處理,然后利用兩種群進化和信息交互機制共享最優解,實現配電網的精確定位。隨著分布式電源的接入,配電網已從單向潮流變為雙向潮流,從而降低了現有故障定位方法的準確性。因此,有必要研究一種具有高容錯性和適用于含分布式的配電網絡故障定位方法。
在此背景下,本文提出了一種用于配電網故障定位的改進量子遺傳算法。使用基于梯度下降的動態門策略更新量子門,并使用Tent混沌優化方法跳出局部最優,通過仿真對該算法的準確性和有效性進行驗證。
1 含DG配電網故障定位方法
隨著配電網中分布式電源(distribute generation,DG)的接入越來越多,對其安全性提出了更高要求[7]。同時,也出現了新的問題,特別是潮流方向由單變雙,使得某些故障定位方法無法應用[8]。在本文中,使用量子遺傳算法(quantum genetic algorithm,QGA)對故障數據信息進行分析,定位故障區域。算法主要有開關編碼、開關與饋線聯絡函數、目標函數三個方面。
1.1 編碼方式
含分布式電源的配電網與傳統配電網絡之間的最大區別是雙向流動問題。為了簡化編碼,如果在配電網饋線部分存在分布式電源,則定義從系統電源到分布式電源為正方向[9]。如果饋線部分中沒有分布式電源,正方向為電源到負載方向,這里正方向僅用于編碼,非實際功率方向。
如果每個開關節點配電開關監控終端(feeder terminal unit,FTU)檢測的故障電流方向與定義正方向相匹配,則報告的狀態信息為1。如果FTU檢測到的故障電流穿越的方向與定義正方向不匹配,則報告的狀態信息為-1。如果沒有故障電流流過,則報告狀態信息為0。表1所示分布式電源的開關編碼模式。

表1 開關編碼方式(含DG)
1.2 開關與饋線間的聯絡方式
在具有分布式電源的雙向配電網中,線路在故障后,安裝在線路上的FTU檢測狀態信息由原始0/1狀態變為-1/0/1。因此,有必要建立一個適當的數學模型來反映開關和饋線之間的信息交互[10]。圖1為簡單配電網模型(含DG)。
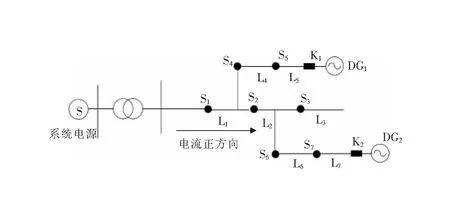
圖1 配電網模型(含DG)
當流過故障電流越線信息的方向與文中定義的正方向一致時,故障電流為正向,不一致為反向。從圖1可以看出,開關S2在饋線L2、L3、L6、L7故障的情況下,S2的故障電流為正向,在饋線L1、L4、L5故障的情況下,S2的故障電流為反向。K1、K2為分布式電源的并網開關。
故障定位系統在至少一條饋線故障或FTU信息出錯時開始運行[11]。開關與饋線之間的聯絡方式如式(1)和(2)所示。
(1)
xi+yj=m(i、j=1,2,3,……,m)
(2)
式(1)由兩部分組成。下游饋線部分和上游饋線部分與下游分布式電源的乘積。在下游沒有分布式電源的情況下,該部分為0,所有開關節點上、下游減法運算[12]。表2所示所有開關上游和下游饋線部分。
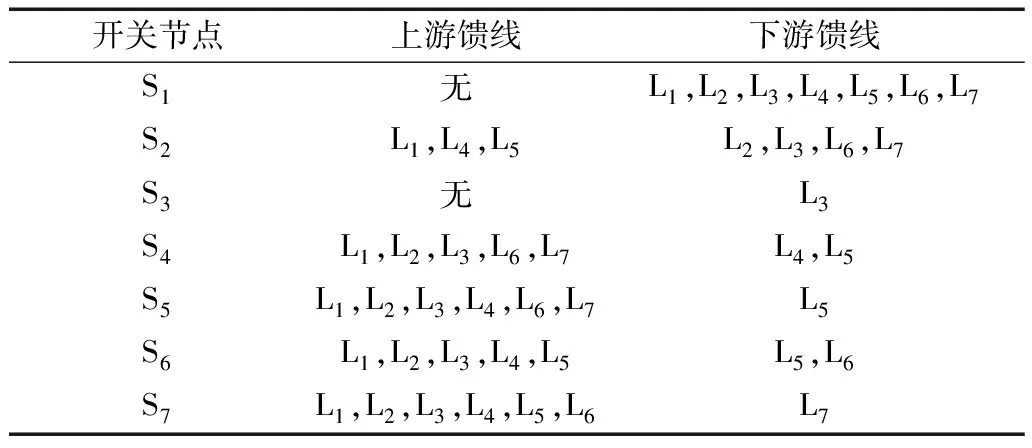
表2 開關節點和饋線關聯
1.3 目標函數
上述方法改善了各開關的編碼以及與饋線間的聯絡方式,能夠正確反映與饋線間的關系,目標函數不受分布式電源影響[13]。目標函數如式(3)所示。
(3)
在式中,I(Sm)為第m個FTU傳饋線狀態信息,取值為-1/0/1;N為開關 總數;X(Se)為故障饋線數;w為防止誤判權重系數,一般為0.5。如果FTU上傳狀態信息與期望的狀態匹配,則目標函數Fmin取最優值。
2 改進算法
2.1 調整量子旋轉門策略
QGA算法使用固定旋轉角策略。本文改良為動態自適應角策略,大幅提高了算法的收斂速度[14]。旋轉角在初期賦予較大的值,隨著不斷進化,使用梯度下降法逐漸減小旋轉角。采用如下方法確定方向和大小。
1)量子旋轉門的方向確定。
令α0和β0為某量子當前搜索的全局最優解的概率幅。α1和β1為相應量子位的當前解的概率幅,如式(4)所示。
(4)
然后根據以下規則選擇旋轉角度δ的方向:當δ≠0時,方向為-sgn(δ);當δ=0 時,當前方向可以為正或負。
2)量子旋轉門大小確定。
采用梯度下降法優化旋轉角度。當目標函數變化率較大時,減小旋轉角步長,變化率較小時,增加旋轉角步長。式(5)~式(7)所示[15]。
(5)
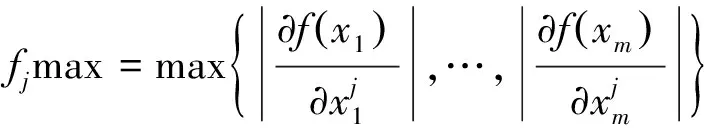
(6)
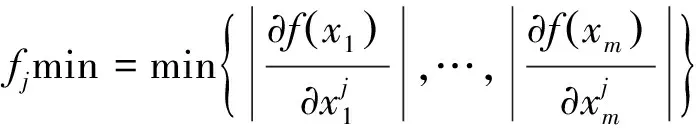
(7)
對于離散數據,梯度是相鄰兩代之間的一階差,(0,μVSmax]如式(8)~式(10)所示。
(8)
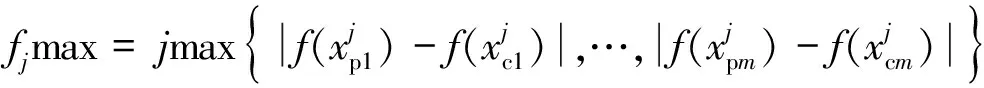
(9)
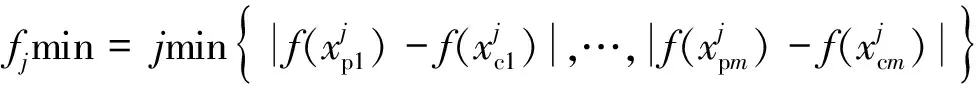
(10)
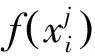
2.2 跳出局部最優解
離散度分析作為測量數據分布程度的方法,主要從數據集中程度和數據分散程度兩個方面反映了數據變化的趨勢[16]。如果為局部優化,則目標值趨于平穩,離散度小。因此,基于每個迭代過程,離散分析方法可以用于分析每個個體的目標值,并確定其是否是局部最優值。離散系數VS的上限VSmax,下限為0。即VS∈(0,VSmax]。如式(11)~式(13)所示。
(11)
(12)
(13)
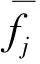
VS接近0,種群目標值越集中,接近VSmax,種群越離散,設定閥值,μ在(0.01-0.5)取值。在每次迭代期間,如果VS值介于(0,μVSmax]之間,則種群陷入局部最優,必須優化擾動此代的種群。如果VS值介于(μVSmax,VSmax]之間,則種群的個體目標值被認為是非常離散的[17]。記錄當前的擾動次數m,超過10次結束優化。
在QGA算法進化中引入了混沌優化思想。增加算法種群的多樣性,從而跳出局部最優Tent映射是具有均勻概率密度、功率譜密度和理想相關性。表達式如式(14)所示[18]。
xn+1=a-1-a|xn|,a∈(1,2]
(14)
Tent映射的Lyapunov指數如式(15)所示。
(15)
當a≤1時,系統是穩定的。當a>1時,系統在無序狀態[19]。當a=2時,這個系統在中心映射中。Tent映射在大數據序列處理中有很大的優勢,但是由于迭代序列很短而且不穩定,因此必須引入隨機方程方法以改善Tent映射。如式(16)所示,對序列xk施加擾動使其跳出小周期或固定點,使系統再次陷入混沌[20]。
(16)
改進的具體步驟如下。
1)步驟一:在迭代過程中,確定第j代種群陷入局部最優,取對應于最小和最大目標值的個體值pjminf和pjmaxf;
2)步驟二:使用向量空間中的歐氏距離dj作為混沌搜索半徑rj的基礎。歐幾里德距離dj是pjminf和pjmaxf兩個個體的向量值距離,如式(17)和(18)所示。
(17)
rj=γdj
(18)
在式中,γ為搜索半徑的倍數;
3)步驟三:獲取0到1之間的隨機數x0,將映射表達式代入生成n×m維序列,將序列號乘以半徑rj,得到新種群的擾動矩陣Δ;
4)步驟四:根據pjminf和pjmaxf個體值的均值pjbzse為基值,將擾動矩陣Δ的每一列向量與pjbzse疊加生成新種群;
5)步驟五:繼續與新物種群迭代,混沌Tent映射良好的遍歷性保證了擾動矩陣在搜索半徑上的分布,提高了新種群的多樣性和后續搜索的準確性。
2.3 改進算法流程
改進的量子遺傳算法在配電網(含DG)中故障定位應用,步驟如下:
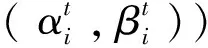
2)步驟二:將每個FTU上傳開關的實際故障信息與目標函數結合起來,以測量組中每個單獨染色體的目標值[21];
3)步驟三:記錄最優目標值對應的個體染色體,作為下一代進化的基礎;
4)步驟四:判斷當前狀態是否進入局部最優狀態。如果進入,就跳出局部最優。如果沒有,更新染色體得到新種群Qt+1{xi},記錄最優個人及其目標價值;
5)步驟五:確定迭代是否結束。如果結束,輸出結果。否則t=t+1,跳到步驟二。流程圖如圖2所示。
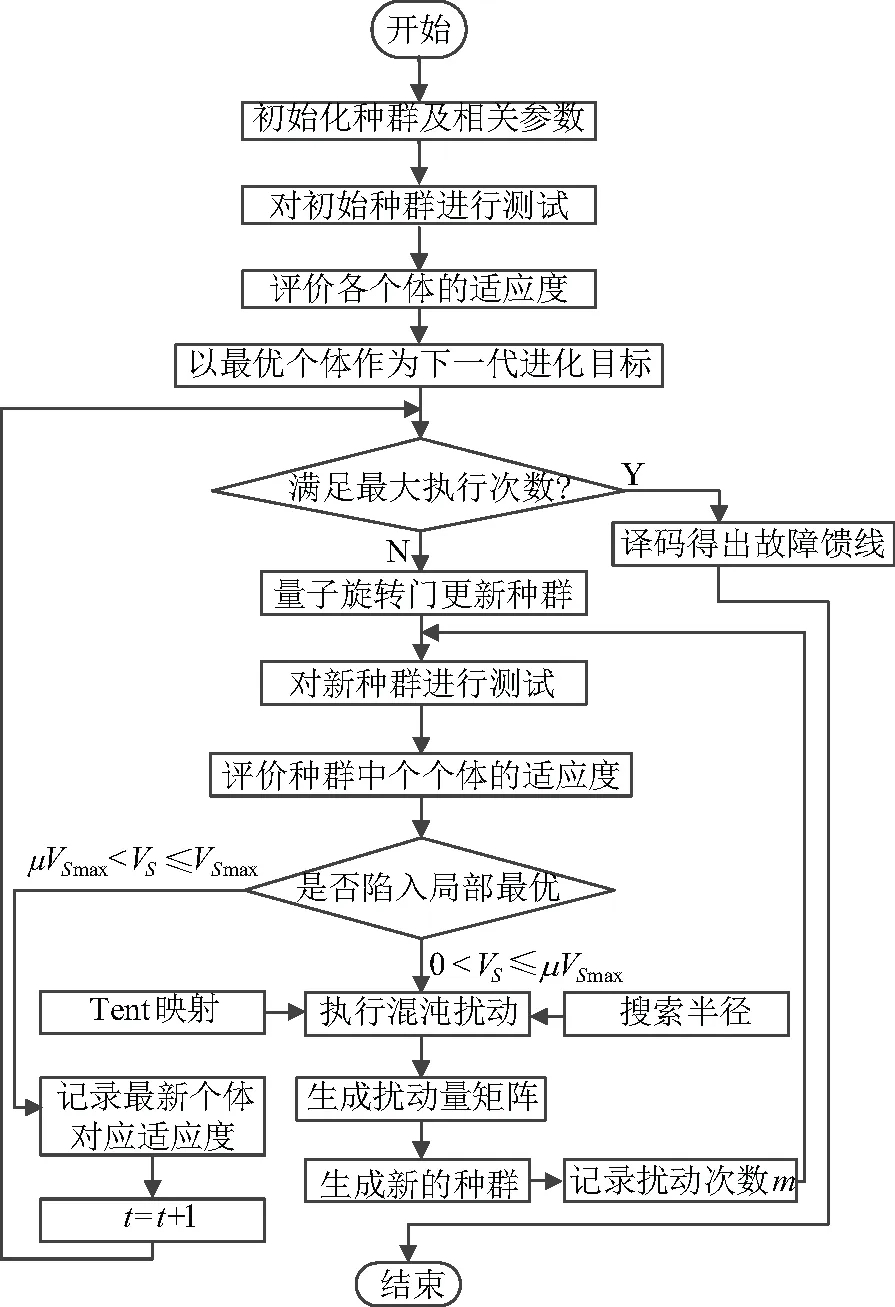
圖2 IQGA算法流程圖
3 實驗結果與分析
3.1 仿真參數
在實際應用中,本文采用IEEE 69節點配電網模型(含DG)。IQGA算法用于配電網故障定位。仿真參數為最大進化代數100、種群大小80,使用改進的旋轉角度策略,離散系數的區間閾值系數μ=0.03。模擬單重和多重故障。圖3所示含分布式電源的IEEE 69節點配電網模型。
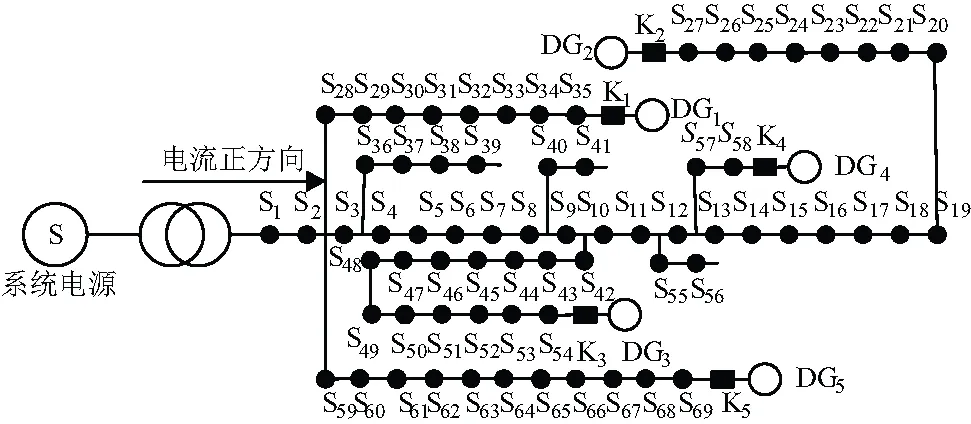
圖3 含DG的IEEE 69配電網
在圖3中,DG1、DG2、DG3、DG4、DG5表示分布式電源。K1、K2、K3、K4、K5是分布式電源并未開關,S1、S2、…、S69是配電網的各開關。L1、L2、…、L69為配電網中的饋線編號。假設每個開關都有FTU故障檢測。為了避免意外結果,將“仿真數”設置為50。
3.2 單重故障分析
如圖3所示,含分布式電源的IEEE-69節點配電網模型,通過仿真對單重故障進行了分析具體故障參數請參見表3。
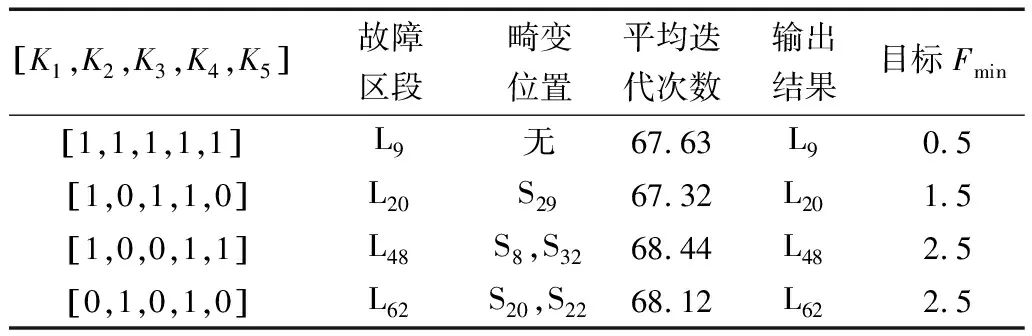
表3 單重故障參數
從表3中可知,將分布式電源連接到電網,L9饋線發生單重故障且沒有畸變失真,則算法的平均迭代次數為67.63,目標值為0.5。當L20饋線有單重故障,則平均迭代次數67.32,目標值1.5。當L48和L62饋線有雙信息畸變單故障發生,則平均迭代次數為68.44和68.12,目標值都為2.5。圖4所示L9饋線單重故障的仿真結果。
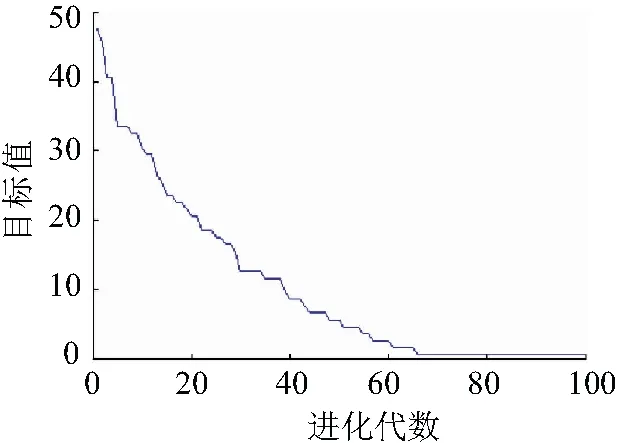
圖4 L9饋線單重故障
3.3 多重故障分析
如圖3所示,含分布式電源的IEEE 69節點配電網模型,通過仿真對多重故障進行了分析。具體故障參數見表4。
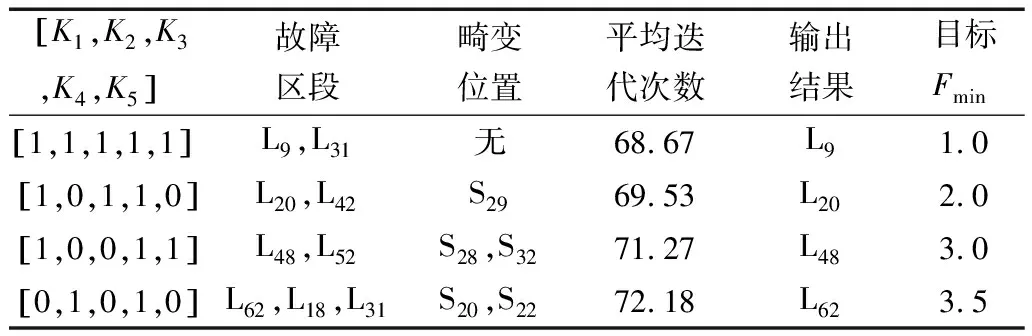
表4 多重故障參數
從表4中可知,將分布式電源并入到配電網時,L9,L31饋線發生多重故障,并且無信息畸變時。算法的平均迭代次數為68.67,目標值1.0。L20,L42饋線中有多重障礙并且單信息畸變時,則平均迭代次數為畸變2,目標值為2.0。圖5所示L20,L42饋線的多重故障仿真結果。
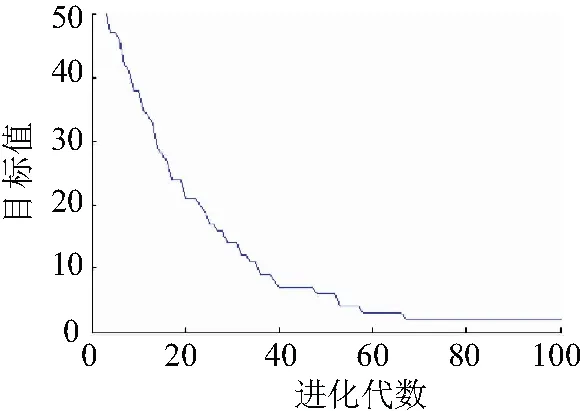
圖5 L20,L42饋線多重故障仿真結果
3.4 算法對比
為了對本文改進量子遺傳算法在配電網故障定位中應用的優越性進行驗證,對表4中的第四種情況使用標準遺傳算法和標準QGA進行仿真比較,進化過程如圖6所示。
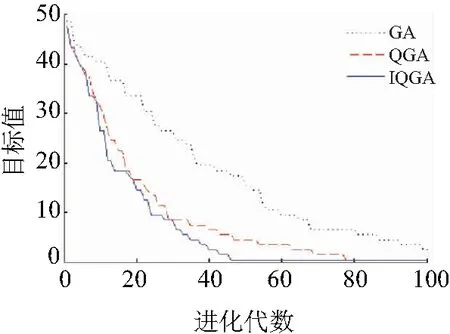
圖6 算法比較
從圖6可以看出本文提出的改進算法收斂速度最快。在45代左右達到最優且波動小。QGA在78代左右找到最優解,而GA在100代尚未達到最優解,并且該算法波動性大且不穩定。因此,與傳統QGA和經典遺傳算法相比,該算法在解決配電網故障方面具有顯著優勢。
仿真結果表明,該算法具有較快的收斂速度和較強的尋優能力。最后,通過與遺傳算法和QGA算法比較。該算法在識別配電網故障方面具有較大的優勢。
4 結束語
針對含分布式電源的配電網故障定位問題,本文提出了一種改進的量子遺傳算法,并通過仿真與改進前算法進行了比較,驗證了該算法的準確性和有效性。結果表明,該方法可以快速有效地定位含分布式電源的配電網故障區段,具有較強的搜索能力和快速收斂性。由于當前實驗室硬件要求和實驗數據的規模,含分布式電源的配電網中故障定位研究仍處于早期階段。在此基礎上,下一步的工作重點將是逐步改進和完善。

